柏木人工林空间结构特征及其评价
付翠林, 汪洋, 孙林山, 林虎, 高树杰, 唐志强*
(1.湖北生态工程职业技术学院,湖北 武汉430200;2.湖北太子山林场管理局,湖北 荆门431800)
柏木(Cupressusfunebris)是柏科(Cupressaceae)柏木属(Cupressus)乔木。柏木为中国特有树种,生长快、用途广且适应性强,是长江以南湿暖地区石灰岩山地的造林树种[1]。京山市湖北省太子山林场管理局现有柏木人工林677 hm2,是国家储备林建设中营造和培育多功能森林的重要战略基地。随着生态环境意识日益提升,人工林的可持续经营和近自然经营越来越受到重视[2-3]。作为可持续经营模式,多目标森林经营注重改善林分空间结构,已被广泛应用于森林质量精准提升[4-5]。多目标经营以森林空间结构改善为经营目标,利用空间结构参数分析林分特征,解释森林林木间的空间位置和竞争态势[6-7]。基于太子山柏木人工林林木空间结构状况,利用空间结构参数建立适地适树的林分空间结构评价模式,以“多功能森林”为经营目标,对于提升柏木人工林森林功能[8-9],促进柏木人工林森林质量具有现实意义。有学者对多目标森林经营理论进行了大量实践应用[10-11],建立了角尺度、混交度和大小比数等结构参数以解释林木的空间分布格局、树种混交程度和树木竞争状况,反映林分内部的结构变化[12]。利用林分空间结构参数在特定置信区间的分布值的多元组合,进一步揭示林分空间结构参数间的生物学关系,已成为多目标森林经营的重要理论基础[13-14]。基于林木空间结构参数均值,应用柯布—道格拉斯生产函数推导出的林分空间结构参数(FSSI)和林分空间结构距离(FSSD)模型,已被广泛用于多种纯林、混交林的群落稳定性评价[15]。
林木空间结构评价是森林经营的依据。林木空间结构参数均值,往往会忽略林木个体间空间结构的差异。林木空间结构的完整性,应以林木个体所在结构单元为基础,以林木空间结构特征值的置信区间为参照[16],建立优化目标评价标准[17]和林木空间评价等级[5,17],从而发现林木所在空间结构特征中存在的具体问题。本研究应用客观赋权法确定各林木空间结构参数权重,建立多目标林木空间结构评价指标,对林木空间结构质量进行分级;借鉴林分空间结构参数(FSSI)和林分空间结构距离(FSSD),综合评价柏木人工林空间结构特征。量化分析林分空间结构参数二元分布信息,探究不同空间结构参数间的生物学意义,从主抓结构的经营思想出发[16],有针对性地实施经营,优化森林空间结构[9],提高林分生产力[14]和固碳能力[2],促进生物多样性,促进柏木人工林的复层化、异龄化和混交化[18],实现多功能储备林建设目标。
1 材料与方法
1.1 研究区概况
太子山林场管理局(112°53′—113°01′E,30°50′—30°59′N)位于湖北省京山市,海拔64~179 m,低山丘陵地貌,黄棕壤,平均土层厚度约30~60 cm。研究区属中亚热带季风气候,四季分明,光照充足,雨量充沛;年均气温16.4 ℃,年均降雨量1 094.8 mm,降雨主要集中在4月—8月,无霜期约240 d,日照时数约为1 969.9 h。
研究区柏木人工林均为皆伐迹地上营造的人工纯林,初植密度为2 000株/hm2。2002—2005年,各林场根据35~55 a柏木纯林生长状况,曾进行过经营择伐。经过择伐、自然稀疏、自然灾害之后,形成不同密度且分布密疏不均的林分。柏木林分内主要混交树种为马尾松(Pinusmassoniana)、冬青(Ilexchinensis)、黄连木(Pistaciachinensis)和乌桕(Sapiumsebiferum)等,种类较少且分布零星。
1.2 标准地设置与调查
2020年7—8月,对研究区柏木林进行了全面踏查。分别在仙女林场、雁门林场和石龙林场选取土壤、地形等环境条件相似、林相整齐的2种密度(约500株/hm2和约1 000株/hm2)柏木林分,设置3个50 m×50 m的标准地和1个40 m×40 m的标准地。记录各标准地的地理坐标、地形条件等基本信息。采用邻接格子法,在每个标准地内依次设置10 m×10 m的木本植物小样方作为样木因子单元,以小样方西南角为坐标原点,测量每株木本植物在样方内的相对位置坐标(xi,yi)。记录样方内木本植物的种名、测量胸径(≥5 cm)、树高和冠幅。以每块标准地西南角为标准地原点对小样方内所测每株木本植物的相对坐标做全局化处理(见表1)。

表1 柏木标准地基本概况Table 1 Basic situation of the planted Cupressus funebris stands
1.3 林分空间结构参数
选取角尺度、大小比数、混交度、林层参数[16]分析柏木林分空间结构基本信息。
(1)应用角尺度说明林木空间分布,公式如下:
(4)
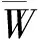
(2)应用混交度说明树种的隔离程度,公式如下:
(5)
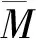
(3)应用大小比数说明林木大小分化,公式如下:
(6)
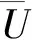
(4)应用林层参数表达林层多样性,公式如下:
(7)

1.4 林分空间结构评价
1.4.1 林木单元结构评价
选取角尺度Wi、大小比数Ui、混交度Mi和林层参数Si,应用乘除法对4个空间结构参数进行多目标规划[17,19]。乘除法将正效益参数与负效益参数的乘积作为评价参数依据,以取大为优,评价参数值越大表明林分空间结构越接近经营者想要的理想状态[20]。本研究以随机分布Wi=0.5为最优值[14],将角尺度Wi∈(0,1]范围的所有数据同时减去0.5,所有数据取绝对值,得到转化后的角尺度值Wia∈(0,0.5],取小为优;大小比数Ui取小为优;混交度Mi和林层参数Si取大为优。
CRITIC赋权法兼顾评价指标间对比强度和冲突性[21],可综合衡量各参数权重。公式如下:
(8)
(9)

根据林木空间结构参数和权重,构建林木空间结构评价函数P(a):
(10)
式中,Si、Mi、Wia和Ui分别为林层参数、混交度、转化后角尺度和大小比数;WS、WM、WW和WU分别为林层参数、混交度、角尺度和大小比数的权重。
将林分空间结构评价参数值归一化,并将评价参数值分为5个等级:[0,0.2)、[0.2,0.4)、[0.4,0.6)、[0.6,0.8)、[0.8,1.0],分别对应林分空间结构评价等级的Ⅰ级到Ⅴ级[17],等级越高表明越接近理想林分空间结构。换算公式为:
(11)

1.4.2 林分空间结构评价
应用FSSI和FSSD评价林分稳定性[15]。
FSSI=[M(100-U)×2W]0.3333,W≤50
(12)
FSSI=[M(100-U)×2(100-W)]0.3333,W>50
(13)
式中,0≤FSSI≤100。FSSI值越大,林分的空间结构越合理,整体林分也越稳定[22]。
(14)
式中,0≤FSSD≤150。FSSD值越大,距离理想状态差距越远,林分越不稳定[15]。
1.5 数据处理与分析
每块标准地设置3 m宽带状缓冲区,消除边缘效应。应用Winkelmass 1.0、Excel 2007和Matlab 2016a处理数据;应用Matlab 2016a绘图。
2 结果与分析
2.1 林分结构均值分析
2.2 林分空间结构评价
2.2.1 林分空间结构评价
应用CRITIC赋权法确定4个柏木标准地林木所在单元结构的角尺度、大小比数、混交度和林层参数的权重(见表3)。根据林木空间结构参数与林木空间结构评价目标,依据各标准地权重,用乘除法建立多目标评价参数,并对评价参数进行归一化处理,评价参数的取值范围为[0,1.0]。将4个柏木林木空间结构评价参数值等距划分为5个评价等级,分别描述林木的空间结构特征(见表4)。

表2 柏木林空间结构参数均值Table 2 Average values of spatial structure characteristics of Cupressus funebris plots
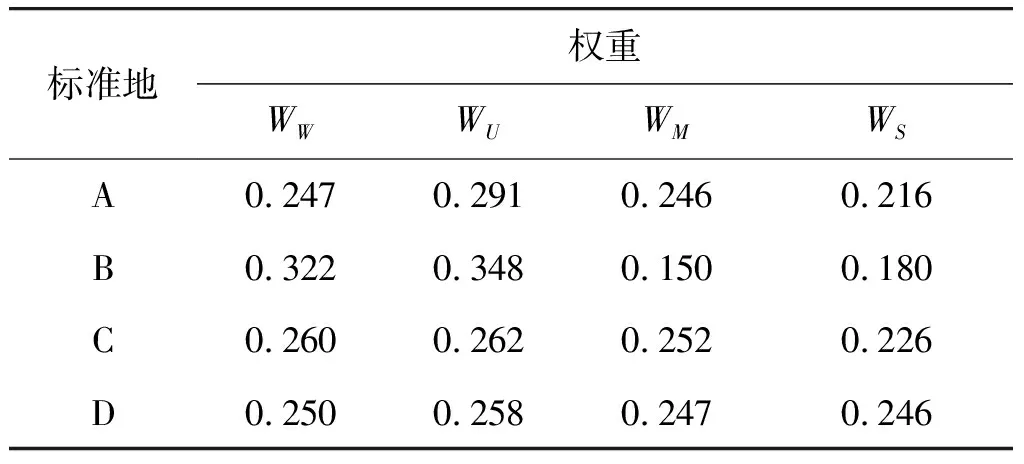
表3 柏木人工林空间结构参数权重Table 3 Weight of spatial structure indexes of Cupressus funebris plots

表4 柏木人工林空间结构评价参数特征Table 4 Characteristics of evaluation index of trees’ spatial structure of the Cupressus funebris plots
根据柏木林分的空间结构参数,评价等级从Ⅰ级到Ⅴ级,等级越高表明林分空间结构越接近理想状态。4个标准地林分空间结构差(Ⅰ级)的单元比例分别为56.41%、93.85%、66.67%和75.71%,其中标准地B的林木空间结构为Ⅰ级的比例最高。标准地A有14.10%、标准地B有4.62%、标准地C有13.24%、标准地D有5.24%的林木空间结构达到理想状态(Ⅲ级~Ⅴ级)(见表5)。
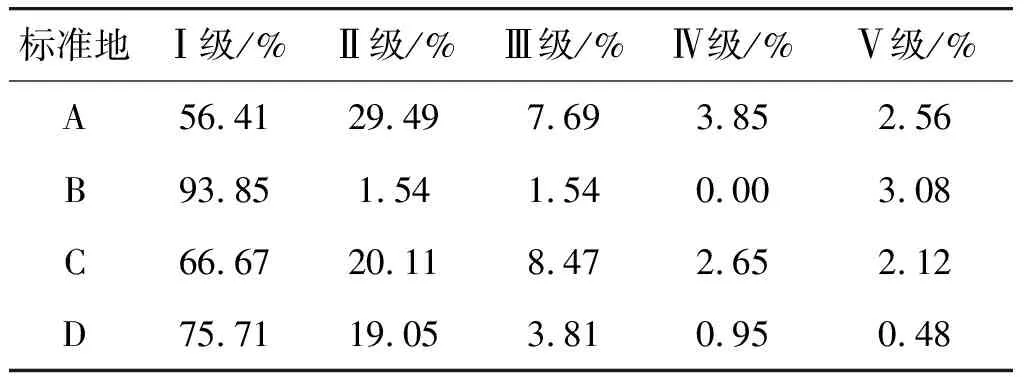
表5 柏木人工林林木空间结构评级Table 5 The grade of individual trees in spatial structure of Cupressus funebris plots
2.2.2 林分空间结构指数与距离
由表6可知,标准地A的FSSI最大,为54.539;标准地D的FSSI为48.809;标准地C为46.006;标准地B的FSSD最小,为29.601。标准地B的FSSD最大,为106.644;其次为标准地C,为93.674;标准地D第三,为87.443;标准地A最低,为82.968。标准地A、C和D林分空间结构基本一致。标准地A林分空间结构相对最优,标准地C和D居中,标准地B空间结构不佳,距理想林分空间结构距离差距较大。
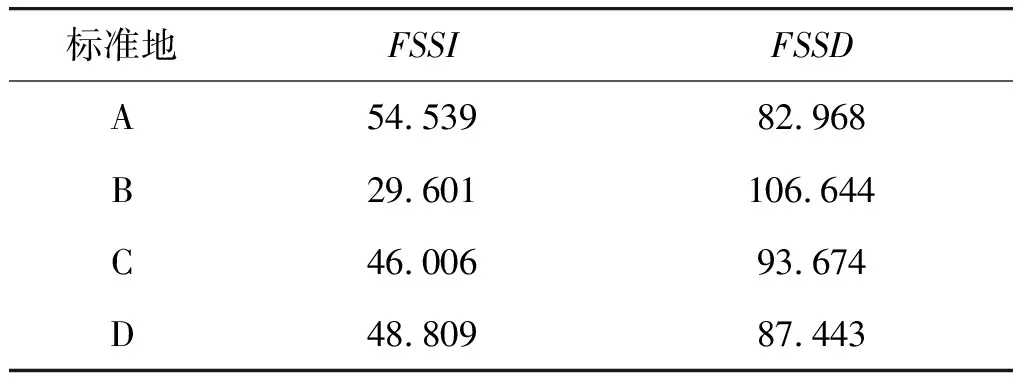
表6 林分FSSI与FSSDTable 6 Stand spatial structure index and spatial structure distance index
2.3 林木空间结构二元分布
2.3.1 角尺度和大小比数二元分布
林木W-U二元分布见图1。标准地A林分(图1A)处于随机分布(W=0.50)的相对频率之和为48.7%,均匀分布(W=0.25)时频率之和为23.1%,弱聚集分布(W=0.75)的频率之和为19.2%;U在[0.00,1.00]区间分布频率之和为在15.4%~24.4%变化;随着W的增大,对应U的频率先增大后减小,随机分布时,U最大。标准地B林分(图1B)处于随机分布状态的频率之和为40.0%,在较均匀分布时频率之和为43.1%,其他分布比例较小;U在[0.00,1.00]区间分布频率之和在18.5%~23.1%间,变化较小;随着W的增大,对应U的频率在W=0.25时达到最大值,后逐渐减小到0。标准地C林分(图1C)林分主要呈随机分布,相对频率为56.1%;U在[0.00,1.00]区间频率之和在18.0%~21.7%间变化较小;W-U的交叉频率在随机分布时达到最大值,后逐渐减小。标准地D林分(图1D)处于随机分布状态的频率之和为47.6%,较均匀分布时相对频率之和为35.7%;U分布频率之和在18.1%~21.4%间,变化较小;W-U交叉频率表现为U在W的[0.00,0.75]区间先升后降,U在随机分布时达到最大值,后大幅减小。
2.3.2 角尺度和混交度二元分布
林木W-M二元分布如图2所示。标准地A林分(图2A)处于随机分布状态(W=0.50)的频率之和为48.7%,并以W=0.50为中轴线略左偏离正态分布;零度混交(M=0.00)时相对频率之和为48.7%,随机分布与零度混交相对频率达到最大值,为23.1%。标准地B林分(图2B)处于较均匀分布状态(W=0.25)的频率之和为43.1%,随机分布时的频率之和略低,为40.0%;M=0.00时相对频率为83.1%,零度混交和均匀分布(W=0.25)交叉频率最大,为38.5%。标准地C林分(图2C)以随机分布为主,相对频率和为56.1%,较均匀分布时频率之和为22.8%;M=0.00时分布频率之和为66.7%;随着W的增大,M的相对频率先增大后减小,随机分布和零度混交交叉频率最大,为34.9%。标准地D林分(图2D)处于随机分布状态的频率之和为47.6%,较均匀分布时频率之和为35.7%;M在[0.00,1.00]区间分布频率之和分别为40.5%、30.0%、10.5%、11.4%和7.6%,林分以零度混交和弱混交为主;随机分布和零度混交时交叉频率最大值为18.6%。

图1 柏木标准地角尺度—大小比数二元分布Figure 1 Bivariate distributions of neighborhood comparison vs uniform angle of Cupressus funebris stands
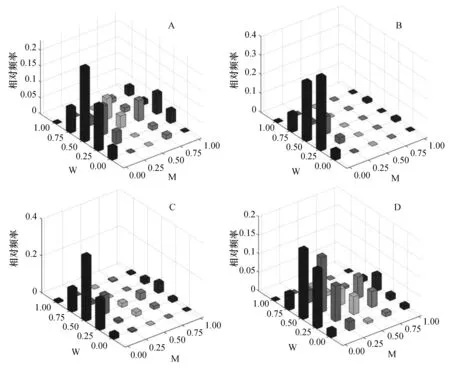
图2 柏木标准地角尺度—混交度二元分布Figure 2 Bivariate distributions of mingling vs uniform angle of Cupressus funebris stands
2.3.3 大小比数和混交度二元分布
林木U-M二元分布如图3所示。标准地A林分(图3A)零度混交(M=0.00)频率之和为48.7%,M频率之和在[0.25,1.00]区间分布在10.3%~15.4%变化;U在[0.00,1.00]区间变幅为14.1%~24.4%,分布较为均匀;U-M交叉频率在零度混交和绝对劣态(U=1)时达到最大值,为12.8%。标准地B林分(图3B)零度混交占绝对优势,相对频率之和为83.1%;U的相对频率之和在[0.00,1.00]区间在18.5%~23.1%间变化;U-M交叉频率在零度混交和劣态(U=0.75)时达到最大值,为20.0%。标准地C林分(图3C)零度混交时频率之和为66.7%,占绝对优势;M在[0.00,1.00]的相对频率之和变幅为4.2%~13.2%;U在[0.00,1.00]区间频率之和在17.5%~21.7%间中庸分布;U-M交叉频率在零度混交和优势态(U=0.00)时达到最大值,为15.3%。标准地D林分(图3D)零度混交和弱度混交时频率之和分别为40.5%和30.0%;U在[0.00,1.00]区间频率之和在18.1%~21.4%区间中庸分布。U-M交叉频率在零度混交、弱度混交与中庸(U=0.50)和劣势(U=0.75)时最大。
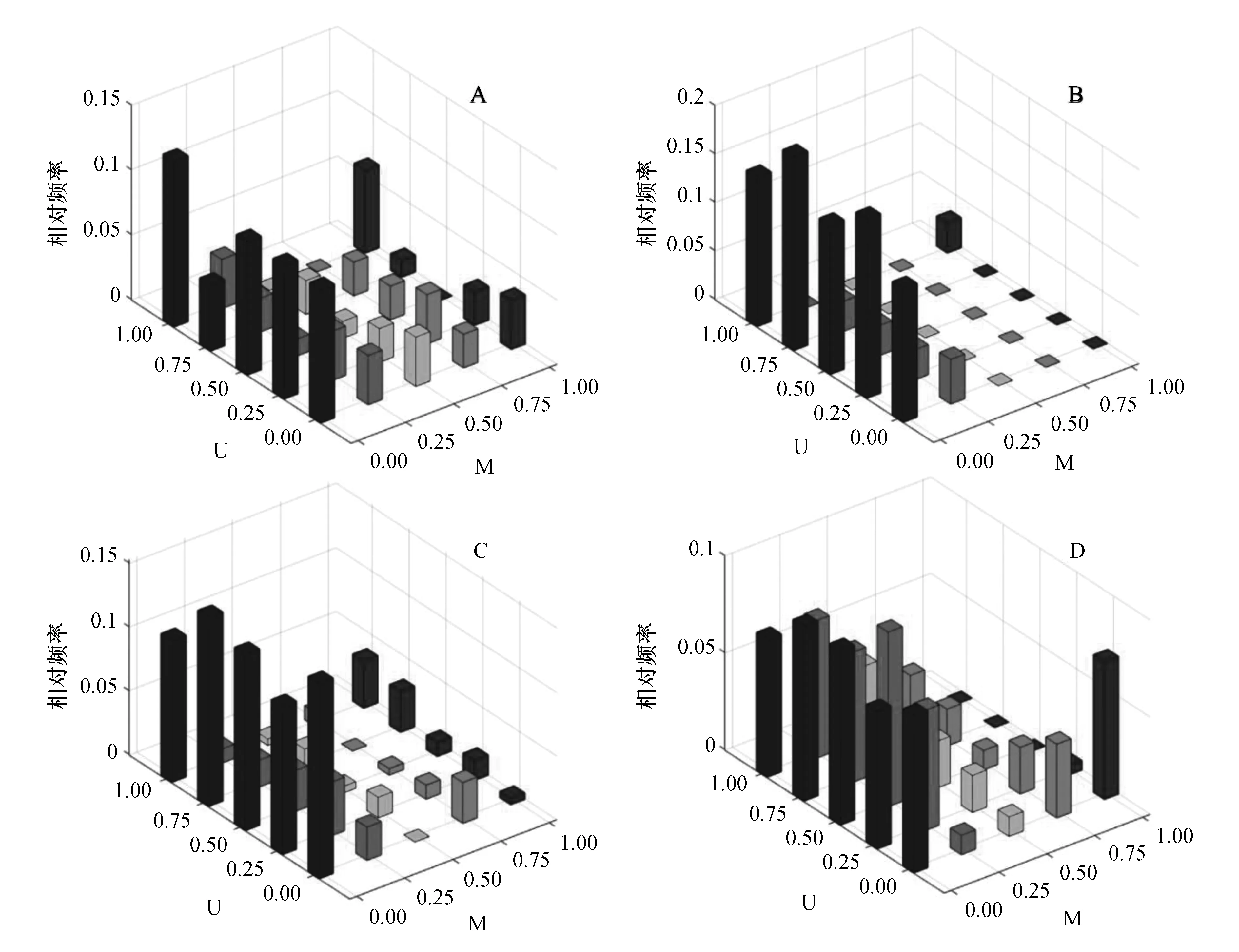
图3 柏木标准地大小比数—混交度二元分布Figure 3 Bivariate distributions of minglingvs neighborhood comparison of Cupressus funebris stands
3 讨论与结论
3.1 林木空间结构特征及其评价
建立林木所在林分的空间结构评价参数体系和评价标准,可确切定位具体林木的空间结构条件,诊断林分空间结构存在问题,以便制定针对性经营措施。CRITIC赋权是以评价指标差异性和评价指标间的冲突为基础确定指标的客观权数,考虑同一指标变异性大小,兼顾评价指标之间的相关性[21],适宜解释不同评价指标间生物学关系,与二元分布所解释的不同结构参数间生物学意义类同,可充分利用数据自身的客观属性对林分空间结构进行科学评价。乘除法多目标规划与空间结构参数正向与逆向转化定量相结合,评级单木所在林分的林分空间结构,相比于林分平均水平更加精准。FSSI和FSSD基于微观经济学柯布—道格拉斯生产函数[15],当林分混交程度最高(M=100),林木分化程度不明显(U=0),水平格局趋于随机分布(W=50)时林分最稳定,且林分距离理想状态最近。建立单木林分空间结构评价参数和评价标准,结合林分稳定性评价模型,不仅能了解林木空间结构的细微状况,也能知晓林分空间的整体状况,并为森林空间结构优化调整提供理论基础。客观赋权法充分利用了样本数据确定参数权重,但对参数在总体目标中的重要性解释不足。因此,在实际林分评价中可采用主客观结合赋权,以实现经营总体目标。
3.2 林分结构二元分布特征

林分角尺度略偏离随机分布,大小比数值偏中庸,低混交度林分是空间结构参数不理想的主要原因。柏木人工林林木随机分布有利于提高林木树种的混交度,减缓林木间大小比数的差异程度。适度的林分密度干扰能维持较高的物种多样性,提高树种混交度有利于减缓林木间的竞争程度。以标准地林分空间结构分析与评价为依据,开展合理抚育间伐并补植乡土阔叶树种,使林分逐渐趋向随机分布、优势态竞争和最高混交,促进柏木人工林可持续经营。

