非圆齿轮往复摆动机构反求设计及运动分析

史 诺,刘 琼,杨晓龙 ,李 笃

(西安航空学院 a.机械工程学院；b.计算机学院，西安 710077)

0 引言

往复摆动是常见的运动形式，目前应用较多的机构是连杆机构和凸轮机构。在高速运动条件下，连杆机构的惯性力不易平衡，且一般只能近似实现给定运动规律；凸轮机构往往需要借助于弹簧来形成力的封闭，额外的动载荷会导致冲击、噪声增大，影响运动特性[1]。齿轮机构的动载平衡、传动精确，但是单纯采用圆柱齿轮的机械机构很难生成复杂的运动规律，非圆齿轮是一种瞬时传动比按一定规律变化的机械零件[2]，将其作为一种函数发生装置运用在轮系当中[3-4]，可以生成往复摆动规律，且具有较为优良的动力学特性。

戴威骏[5]采用三个非圆齿轮与三个圆柱齿轮构成定轴轮系，可以输出规律的变速摆动，实现了无游梁式抽气机的平稳换向；刘永平等[6]构建了行星轮系使输出端做往复摆动运动，实现了抽油机的机械式换向，在此结构中，非圆齿轮采用的是椭圆齿轮，通过改变椭圆齿轮的偏心率实现运动规律的调节；章伟[7]利用行星轮系构造了织机打纬机构，打纬揺轴的运动学性能达到了理想状态，在该机构中，两对啮合的齿轮均采用了非圆齿轮，机构的设计难度较大。

上述研究对于非圆齿轮往复摆动机构的设计奠定了一定的理论基础并提供了典型范式，为了进一步降低设计难度，本文通过反求设计方法构建W-W型非圆齿轮行星轮系，其分析过程简单，设计结果可靠。

1 往复摆动原理

图1为一个典型的W-W型非圆齿轮行星轮系，由行星架及4个齿轮构成，行星架H是输入端，其转速恒定，转角为φH，非圆齿轮1、2、3、4构成了外啮合的齿轮副G12、G34，其中齿轮1固定不动、齿轮2与3同轴相连，齿轮4是输出端，其转角为φ4，对非圆齿轮行星轮系采用速度矢量图的方式进行运动分析[8-9]。

(a)初始时刻

从理论上来讲，圆柱齿轮是非圆齿轮的一种特殊形式，若齿轮副G12与齿轮副G34之一为圆柱齿轮副，另一个为非圆齿轮副，则每对齿轮副啮合点K、M之间的相对位置变化规律就会更明确，设计非圆齿轮行星轮系的难度就大为降低，因此选定齿轮1、2为圆柱齿轮，3、4为非圆齿轮，后文中对轮系的运动分析在此条件下进行。

2 运动分析及反求步骤

非圆齿轮往复摆动机构设计要解决的关键问题是：在根据实际工况确定输出运动规律以及根据实际传动空间确定大致几何尺寸的约束条件下，反求出非圆齿轮3、4的节曲线。

2.1 运动分析

对行星轮系采用反转法进行分析，即对整个机构施加旋转运动，其转速为-dφH/dt，则行星架H是静止的，行星轮系转化成为定轴轮系[10]，在定轴轮系中可忽略行星架H，如图2所示。

图2 转化轮系结构示意图

(1)

(2)

在原有行星轮系中，齿轮1是固定不动的，故

(3)

(4)

式中，i4H是原有行星轮系的整体传动比。

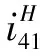
(5)

根据式(4)、式(5)，整理可得：

(6)

根据行星轮系的结构构型，4个齿轮向径之间的关系为：

r1+r2=r3+r4=a

(7)

式中，a为常数，是齿轮副G12、G34的中心距。

将式(7)代入式(6)可得：

(8)

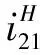
(9)

又齿轮3的转角满足的关系为：

(10)

从而得到了转化机构当中非圆齿轮3的节曲线方程为：

(11)

将式(9)代入式(7)，并与式(2)联立，得到转化机构当中非圆齿轮4的节曲线方程为：

(12)

2.2 反求计算流程

如图3所示，求解非圆齿轮3、4的节曲线的主要步骤如下所述：

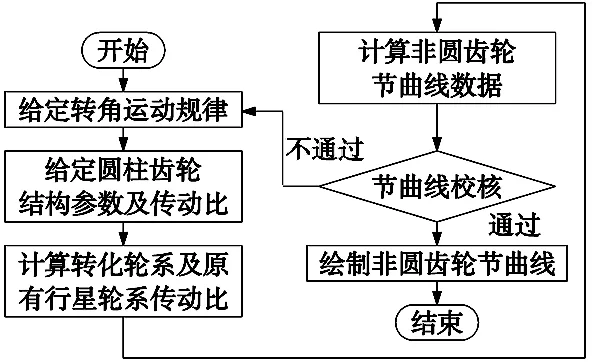
图3 非圆齿轮节曲线绘制流程图

(1)根据实际工况要求确定行星架H在一个回转周期内非圆齿轮4的转角运动规律；

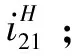
(5)对节曲线进行封闭性校核、压力角校核、根切校核，若符合传动与制造要求，将步骤(4)获得的离散点数据采用三次样条插值后绘制出非圆齿轮的节曲线，若不符合要求，优化参数后从步骤(1)开始重新计算，直至校验通过。

2.3 设计实例

设定在行星架H的一个回转周期内，非圆齿轮4往复等角摆动，其角位移呈简谐运动规律，最大转角φ4m为π/3，最大转角φ4m所对应的行星架H回转角度φH为π。根据上述运动要求，则行星轮系的转角关系为：

(13)

根据图3所示的流程，当圆柱齿轮1、2均采用模数为2 mm、齿数为30的结构参数，计算得到中心距a为60 mm，此时反求得到的非圆齿轮3、4的节曲线如图4所示。

(a)非圆齿轮3的节曲线 (b)非圆齿轮4的节曲线

3 齿轮构型

对非圆齿轮的范成法加工过程进行模拟可以得到包络模型，在此基础上可以生成非圆齿轮的三维实体[11-13]。如图5所示，在非圆齿轮的中心建立固定坐标系XOY，在插齿刀中心建立随动坐标系X0O0Y0，X0轴是插齿刀中心轨迹的切线，Y0轴是插齿刀与非圆齿轮瞬时啮合点的法线，范成加工过程可以视为插齿刀的节圆沿着非圆齿轮节曲线的纯滚动，当初始啮合点E滚动至E′时，插齿刀转过的角度为θ，非圆齿轮对应的转角为φ，随动坐标系X0O0Y0中的Y0轴与固定坐标系XOY的X轴之间的夹角为β。

图5 非圆齿轮的范成法加工原理

在固定坐标系XOY下，插齿刀的中心坐标x0、y0可以表示为：

(14)

式中，x、y是非圆齿轮节曲线上的点坐标；rd为插齿刀节圆半径。

非圆齿轮节曲线上的点坐标x、y计算公式为：

(15)

式中，r为非圆齿轮的向径。

随动坐标系X0O0Y0中的Y0轴与固定坐标系XOY的X轴之间的角度为β，计算公式为：

(16)

将式(15)、式(16)带入式(14)，可以求得在固定坐标系XOY下，插齿刀的中心坐标x0、y0。

将随动坐标系X0O0Y0中插齿刀的齿廓坐标转换至固定坐标系XOY中，其计算公式如下：

(17)

式中，xd、yd是随动坐标系X0O0Y0下插齿刀的齿廓点坐标；X、Y是固定坐标系XOY下插齿刀的齿廓点坐标。

由于在范成过程中插齿刀转角θ对应的节圆弧长与非圆齿轮转角φ对应的节曲线弧长是相等的，故以插齿刀转角θ为自变量，可以计算出非圆齿轮转角φ：

(18)

依据式(17)计算固定坐标系XOY下，不同的非圆齿轮转角φ所对应的插齿刀的齿廓点坐标，连点成线后即可得出非圆齿轮的包络模型，如图6所示。依据包络模型提取齿廓，并赋予一定的齿宽，可得到非圆齿轮的实体模型。

(a)非圆齿轮3的包络模型 (b)非圆齿轮4的包络模型

4 虚拟样机与仿真

在UG NX软件平台的装配模块中将齿轮1与2、3与4进行装配，齿轮副G12与齿轮副G34构建完成后再与机架之间进行约束，得到非圆齿轮往复摆动机构的虚拟样机，如图7所示，保存模型后切换到运动仿真模块进行分析。

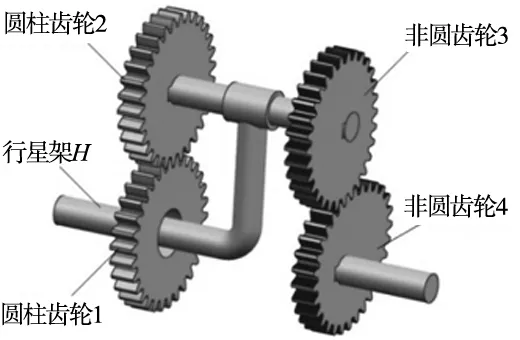
图7 往复摆动机构的三维模型

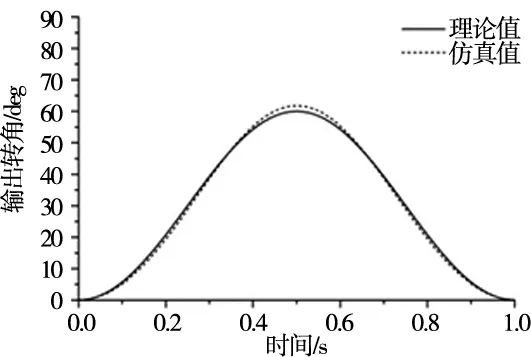
设定行星架的输入转速为360 °/s，仿真时间为1 s，仿真步数为1000步，测定非圆齿轮4的输出转角曲线，并对输出转角曲线关于时间进行微分处理，得到角速度曲线，将仿真得到的输出响应与理论值进行对比，如图8所示。

(a)角位移曲线

从图8a可以看出，角位移理论值与仿真值较为接近，在0.5 s时理论值与仿真值均达到了最大，角位移的理论最大值为60°，仿真最大值为61.792 6°，误差为2.99%，误差是由节曲线的设计精度造成的，节曲线是由离散点数据经过三次样条插值后拟合得到的，离散点越多，则节曲线的精度越高，要降低误差，需要增大节曲线的数据计算量；从图8b可以看出，角速度的理论值与仿真值的变化趋势是一致的，说明行星轮系的设计是正确的，但是角速度仿真值一直是波动状态，造成这种现象的主要原因一是每一次轮齿的啮合均会形成刚性碰撞；二是非圆齿轮传动过程中的重合度不断变化。在多重影响因素下整个行星轮系产生了非规律性的振动，在此激励下角速度仿真值呈明显的锯齿状。根据行星轮系运行时的工况，仿真值相对于理论值更能反映出实际状态[14]。

5 结束语

从往复摆动的运动原理出发，利用非圆齿轮构建W-W型行星轮系，并建立虚拟样机进行了运动分析，可以得到如下结论：

(1)W-W型非圆齿轮行星轮系中两个齿轮副啮合点之间的相对位置变化是产生往复摆动运动的原因，将其中的一对非圆齿轮副特殊化为圆柱齿轮副，则啮合点之间的相对位置变化规律较为明确，大大降低了机构的分析与设计难度。

(2)根据摆角运动规律反求非圆齿轮节曲线，在此基础上模拟范成加工过程获取非圆齿轮包络模型，提取齿廓并赋予一定的齿宽，可得到非圆齿轮的实体模型。

(3)非圆齿轮往复摆动机构仿真测试输出的角位移曲线、角速度曲线与理论分析的吻合度较高，在变化趋势上是一致的。

(4)W-W型非圆齿轮行星轮系不仅可以实现往复摆动运动而且可以完成摆动—回转运动、间歇旋转运动、间歇摆动等，这就需要将节曲线表示成分段函数的形式，再进行齿轮构型后完成机构设计，其基本分析流程与设计步骤与本文一致。