一类非线性演化不等方程弱解的不存在性
李钰强
(广西师范大学 数学与统计学院,广西 桂林 541006)
0 引言
在欧氏空间RN上,关于椭圆型、抛物型和双曲型的不等方程解的存在性以及应用已经有了许多研究[1-4].在RN中,椭圆不等方程为
-∇·(|∇u|p-2∇u)≥uq,u≥0,u≡0,
(1)
以及在RN×[0,∞)中,抛物型方程:
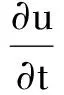
(2)

对于含有Baouendi-Grushin算子不等方程也有如下的结果:
(3)
(4)
其中:ΔG定义为:ΔG:=Δx+|x|γΔy;a是有界可测函数;γ,δ1,δ2≥0.由准均匀条件诱导出的距离为
(5)
在文献[6]中已经证明不等方程(3)和(4)的非平凡弱解的不存在性.
根据文献[6],文献[7]研究了某类p-Laplace型Baouendi-Grushin算子不等方程弱解的存在性.文献[8]研究了含p-Laplace型Baouendi-Grushin算子方程解的梯度估计.
本文根据参考文献[9],在Rn×Rm×[0,∞)中,对含p-Laplace型Baouendi-Grushin算子的抛物型不等方程:
(6)

1 预备知识
Baouendi-Grushin向量场∇G定义为(参考文献[11]):
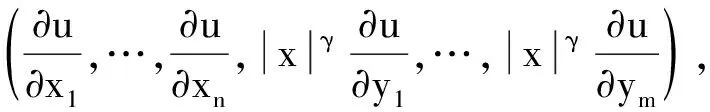
设A=|∇Gu|p-2∇Gu:RN×R×RN→RN,则A满足
(A,∇Gu)=|A|p′,
(7)
其中:(·,·)为欧式空间的内积;p′为p的共轭指数.
定义1一个非负函数u∈W1,p(RN×[0,∞))

(8)
则称u是方程(6)的弱解.
2 主要结果及证明
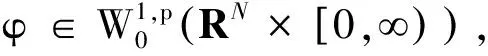
(9)
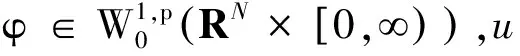

(10)
由(7)和(10),利用Young不等式可得

其中ε>0.
整理得
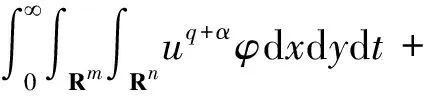

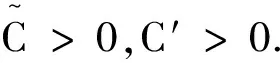
引理2(先验估计)假设引理1成立,设q>max{1,p-1},α<0,且
(11)
其中:Ci′>0,i=1,2,3;κ′,η′,μ′分别是κ,η,μ的共轭指数,κ,η,μ分别为
(12)
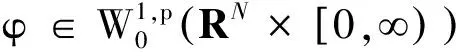
由Holder不等式得
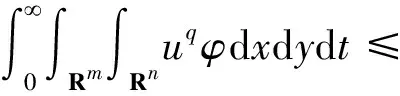
(13)
由(9)可推出

于是由(13)可得

由Holder不等式得
(14)
令
由Young不等式得
其中εi>0,i=1,2,3.
因此,由(14)可得
整理得
其中
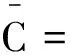
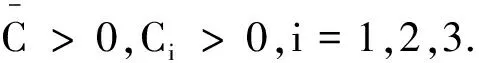
即
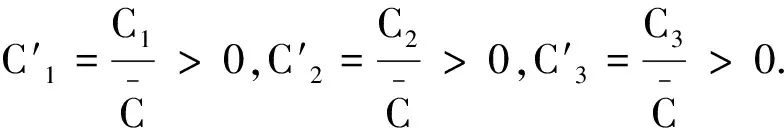
定理1设q>max{1,p-1},且
(15)
若
(16)
则方程(6)不存在非平凡弱解.
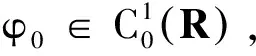
令
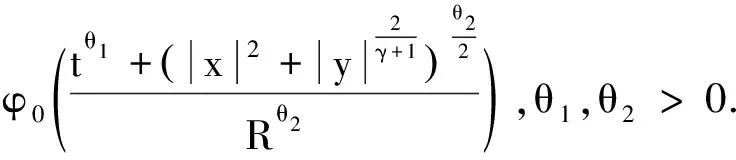
(17)
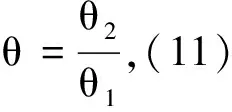
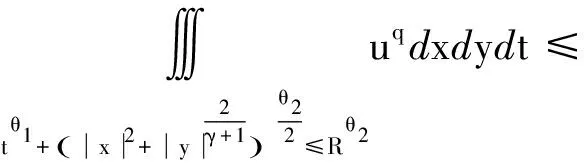
其中
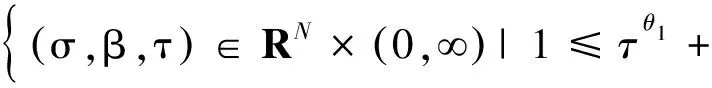
则有
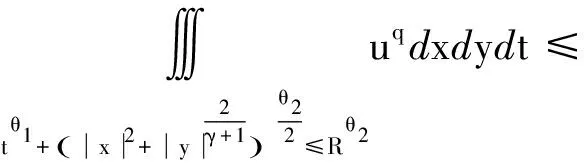
(18)
其中

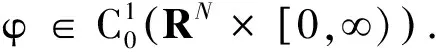
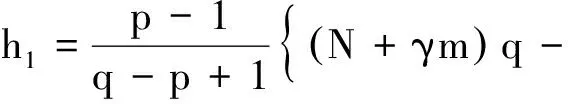
(19)

(20)
其中,
由于u∈Lq(RN×(0,∞)),则存在一个序列{Rl}→∞,l→∞,使得
结合这个极限关系和式(20)得
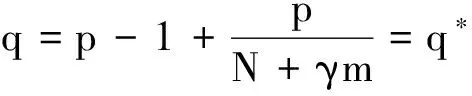
进一步考虑这样的方程:在Rn×Rm×[0,∞)中,设k>0,q>max{k,p-1},p>1,抛物型不等方程:
(21)
同样有以下结果.
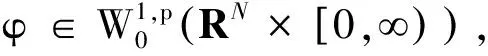
(22)
其中C5>0,C6>0.
推论2(先验估计) 假设推论1成立,设
q>max{k,p-1},α<0,
且
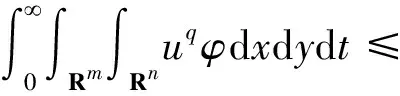
(23)
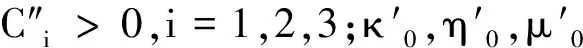
(24)
定理2设q>max{k,p-1},且
(25)
若
(26)
则方程(21)不存在非平凡弱解.
定理2的证明类似于定理1的证明.
3 结语
本文利用一种先验估计的方法,通过试验函数法,研究了一类非线性演化不等方程弱解不存在性问题,可进一步应用到含有p-Laplace型Baouendi-Grushin算子不等方程弱解不存在性的研究中.本文改进了试验函数的选取,控制p的范围,根据q的取值范围对方程(6)弱解的不存在性进行分析,将方程(6)拓展到方程(21).本文的证明方法与过程可为某类抛物型不等方程弱解的不存在性提供一些研究思路.

