基于KS检验的U-型设计组合同构判别
方湘豫,雷轶菊,欧祖军
(1. 吉首大学 数学与统计学院, 湖南 吉首 416000; 2. 新乡学院 数学与统计学院, 河南 新乡 453003)
0 引言
部分因析设计广泛应用在工业和科学研究中.两个部分因析设计称为是组合同构的,如果其中一个设计可由另一个设计通过重新安排试验顺序,重新标记因子和置换水平得到.由于两个组合同构设计在同一个经典的方差分析模型中有相同的统计性质,故被认为是等价的.从统计学的角度看,非组合同构设计的判别不仅扩大了随机设计的种类,而且扩大了各种效率准则的取值范围,例如文献[1]中的p-准则的取值范围,因此对组合同构设计的判别就显得十分重要.
部分学者提出了一些设计组合同构的检测方法.两个组合同构设计的对应试验点间的Hamming距离在所有维度上相等.文献[2]基于该结论提出了检测两个设计是否同构的算法.此外,文献[3]提出了有效的算法,用来从若干个设计中判别组合同构设计,并要求在识别程序之前将这几个设计中的每个设计排列成具体的形式.但文献[3]只给出了判别设计组合同构的充分条件,无法判别两个非组合同构设计.文献[2]和文献[3]分别提出了组合同构检测的方法,除此之外,也有一些学者提出了非组合同构的检测方法.文献[4]基于均匀性测度提出了一个用于检测非组合同构的新的算法,并对该算法提供了理论证明.文献[5]提出了最小低阶混杂优化准则,并证明了非组合同构设计在该准则下是不同的.文献[6]分别基于投影Hamming距离模式和所有水平置换下设计的均匀性测度分布提出了快速投影Hamming距离模式分布算法和水平置换匹配算法,这两个算法能够快速有效地用于检测两个设计是否为非同构设计,其中水平置换匹配算法依次比较两个设计在所有水平置换下的均匀性测度分布的均值、方差、偏度和峰度是否相等,如果在某一步骤上检测出指标不相等,则终止下一步的比较,且判别这两个设计为非同构设计.
与文献[6]不同的是,本文将基于KS检验方法,KS检验是常被用来比较两个总体的分布是否相同的非参数统计方法[7],从假设检验的角度对两个设计在所有水平置换下的均匀性测度的分布是否相等进行检验,以判别两个设计是否组合同构.本文基于KS检验讨论了两个设计是否组合同构.并用该方法对已有文献的例子进行了验证,得到的结果与已有文献中的结果是一致的.
1 预备知识
记d(n;qs)为一具有n次试验、s个q水平因子的设计,设计d中每个因子取自集合{0,1,…,q-1}中的元素.
定义1若集合{0,1,…,q-1}中的q个元素在设计d(n;qs)的每个因子中出现的次数相同,则称设计d为对称U-型设计.
记D(n;qs)为包含所有对称U-型设计d(n;qs)的集合.对任意的设计d∈D(n;qs),d中的每个试验点(vi1,…,vis)可映射为[0,1)s的点(xi1,…,xis),其中xij=(2vij+1)/(2q),i=1,…,n,j=1,…,s.偏差作为U-型设计均匀性的评价标准,用来刻画试验点集在试验区域内散布的均匀程度.目前有很多偏差可以用来衡量设计的均匀性,其中中心化L2-偏差和可卷型L2-偏差都是比较常用的偏差,而混合偏差在很大程度上克服了中心化L2-偏差和可卷型L2-偏差的不足之处[8].
定义2设d∈D(n;qs)为一n次试验、s个q水平的对称U-型设计,设计d的混合偏差可由下面表达式得到,
两样本的KS检验是用来比较两样本的总体分布最常用的非参数方法[8].
设X1,…,Xm和Y1,…,Yn为分别来自总体F和G的独立同分布样本,即X1,…,Xm~F(x),Y1,…,Yn~G(x).两样本的总体分布F和G的假设检验问题为
H0:F(x)=G(x)↔H1:F(x)≠G(x).
当样本量较大时, Glivenko给出了经验分布函数Fn(x)与理论分布函数的F(x)接近程度的大样本度量, 即证明了
由Glivenko定理知, 用经验分布函数Fn(x)近似理论分布函数的F(x)是可行的.于是Smirnov提出了用下面的检验统计量来检验上述假设检验问题:
式中:Fm(x),Gn(x)分别表示总体F,G基于样本X1,…,Xm和Y1,…,Yn的经验分布函数.因此,Dmn愈小,直观上看与原假设H0愈符合;反之,Dmn愈大,则与对立假设H1愈符合.由此,上述检验假设问题的一个直观合理的检验φ为
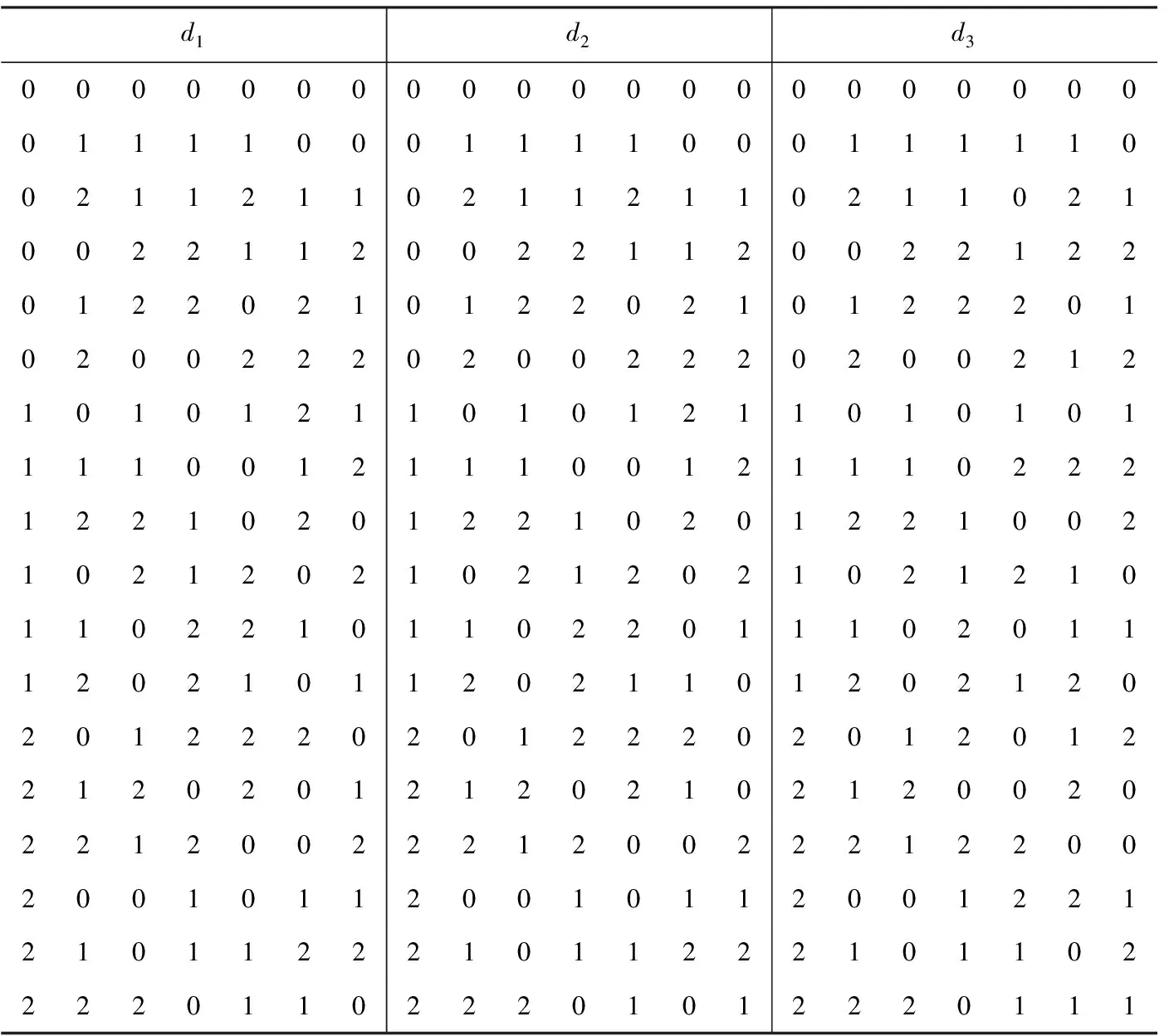
φ:当Dmn 其中:c(α)与检验水平α有关. 当样本量较大时, Smirnov证明给出了在原假设H0成立时, 统计量Dmn的极限分布 这与Kolmogorov[8]在1933年针对单样本的分布拟合问题给出的极限分布只相差一个倍数,故两者可合用一个极限分布表. 对任意两个设计d1,d2∈D(n;qs),讨论基于KS检验方法对设计d1,d2是否组合同构进行判别,该判别方法也适用于任意两个具有相同大小的非对称设计组合同构的判别. 由设计的组合同构定义可知,如果设计d1可由设计d2通过置换一些列的水平得到,则设计d1,d2是组合同构的,但它们不一定有相同的几何结构,也就导致了均匀性测度可能不同,即可能有不同的混合偏差值.另一方面,仅仅通过重新安排试验顺序和重新标记因子这两类操作得到的组合同构设计,它们的混合偏差值不变. 对任意两个设计d1,d2∈D(n;qs),若分别考虑设计d1,d2所有可能的水平置换,则分别可得到设计d1,d2的(q!)s个组合同构设计.记P(d1),P(d2)分别为设计d1,d2的l=(q!)s个组合同构设计的集合.类似地,组合同构的设计在几何结构上可能不同,从而使得组合同构设计的混合偏差值也可能不同. 下面的定理给出了设计d1,d2组合同构判别的理论基础. 本文基于KS检验方法对X1,…,Xl和Y1,…,Yl的总体分布F和G是否相同来实现对设计d1,d2组合同构的判别,其判别的具体步骤如下. 第一步 对任意两个设计d1,d2∈D(n;qs),分别计算设计d1,d2的所有水平置换设计的混合偏差值 第二步 提出假设H0:F(x)=G(x)↔H1:F(x)≠G(x). 第三步 基于KS检验方法,若拒绝H0,则判别设计d1,d2为非组合同构,否则判别设计d1,d2为组合同构. 基于定理1,下面给出了设计d1,d2组合同构判别的具体算法. 算法:判别两个设计d1,d2∈D(n;qs)组合同构. 输入:两个设计d1,d2∈D(n;qs). 输出:设计d1,d2是否组合同构. 步骤: KS检验: 将两组样本合并为一组样本,记为S. whileS不为空do 从S中选择一个样本X0,计算|Fl(X0)-Gl(X0)| end if 从S中删除样本X0 end while 设计d1,d2组合同构 else 设计d1,d2非组合同构 end if 本节中提供了两个数值例子来验证基于KS检验的组合同构设计判别方法的有效性.数值例子表明:基于KS检验的组合同构设计判别方法是非常快速有效的. 例1考虑文献[9]中的三个设计d1,d2,d3∈D(18;37),具体的设计如表1所列.由文献[9]可知设计d1,d2,d3是非组合同构设计.现利用KS检验来对其是否组合同构进行判别,具体数值结果如表2所列. 表1 三个非组合同构设计d1,d2,d3∈D(18;37) 由表2可以发现设计d1,d2,d3间是否组合同构的KS检验结果中的p值全都小于2.2e-16,故原假设H0不成立,即设计d1,d2,d3在所有水平置换下的设计的混合偏差的分布两两互不相同,因此设计d1,d2,d3两两非组合同构,这与文献[9]中的结果是一致的. 表2 设计d1,d2,d3间是否组合同构的KS检验结果 本文基于KS检验给出了一种判别U-型设计是否组合同构的简单的方法,数值例子表明该方法对于设计的组合同构判别非常有效,同时该方法也可推广至非对称U-型设计的组合同构的判别,可为一般结构的设计组合同构研究提供参考. 表3 两个组合同构设计d4,d5∈D(9;33)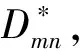
2 基于KS检验的组合同构设计 判别


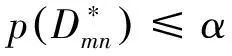
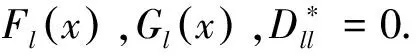
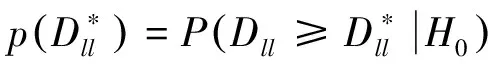
3 数值例子

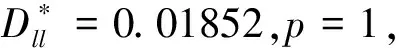
4 结语