一类混合整数规划模型的共享车调度优化算法研究

马艳利,陈明秀

(1.宁夏大学新华学院 信息与计算机科学系, 宁夏 银川 750021; 2.宁夏大学新华学院 工程与应用科学系，宁夏 银川 750021)

0 引言

随着我国经济的快速发展，城市交通问题和拥堵问题日益严重.共享车作为一种新型的出行工具，解决了城市“最后一公里”问题.共享车在运行过程中自发地产生了供需不平衡问题，为了解决这一问题，需要对车辆进行调度，这个调度过程被称为共享车调度问题(bikesharing rebalance problem，BRP).

现有研究中，共享车调度大致分为两类：静态共享车调度(SBRP)和动态共享车调度(DBRP).静态调度相关文献大多都围绕着再平衡操作而确定车辆路线，将所研究区域分割成小区域，用平衡工具进行再平衡操作.不同的文献对所考虑的假设、要优化的目标和要整合的约束条件各不相同，且各有优缺点.文献[1]通过构建最小化货车访问路线总成本的目标函数来实现静态调运，采用迭代局部搜索的启发式算法求解；文献[2]提出若干有效不等式，建立了数学模型，利用禁忌搜索算法求解.由于调度周期长，最优解局限于局部，部分文献考虑调度周期的问题.文献[3]为了满足共享车快速响应调运和降低调运成本的需求，构造了基于分形数的多车场协同调运模型；对动态调度，文献[4]研究的是时变环境下，结合不同类型单车之间的替代特性，建立了混合整数规划模型，并设计了混合禁忌搜索算法对问题进行求解；Kadri[5]提出了一个已知的阈值水平，表示每个站点平衡共享车数量，再平衡需求仅用于满足阈值水平即可.文献[5]采用一个平衡点，平衡操作次数较大，平衡时间较长.本文将站点的平衡定义为平衡区间，代替文献[5-6]中的平衡点，站点内的共享车库存处于这个区间，都属于平衡，可减少平衡次数.另外，本文定义新的评价满意度的指标函数-再平衡效益衡量函数，在此基础上建立以总行程距离最小和再平衡效益衡量函数最大的双目标函数，提出基于变领域搜索的粒子群-禁忌搜索算法对问题进行求解.

本文研究静态共享车再平衡问题(SBRP).文章结构是：第2节介绍了实用的平衡弹性间隔概念，在此基础上定义站点平衡程度的指标-再平衡效益衡量函数，建立以路线最小化和再平衡效益衡量函数最大化的混合整数规划双目标模型，这是本文的主要内容之一；第3节介绍粒子群-禁忌搜索算法，为避免陷入局部最优，提高探索能力，引入3种结构的变异算子；第4节主要是对改进的粒子群-禁忌搜索算法进行收敛性分析.

1 BBS平衡问题描述和数学建模

混合整数非线性规划模型是经典的求解路径最短问题模型，下面是标准的规划模型[7]：

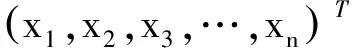
由于整数问题较难求解，将INLP问题转化成其相应的松弛问题NLP,即不考虑决策变量的整数要求，

1.1 平衡弹性区间

在以往的研究中，BSS站的平衡被定义为一个预先指定的平衡点，即站点共享车数量需要达到预定的数量，如文献[5-6]采用这种定义方法.这种定义法需要多次平衡操作，平衡时间较长.本文将平衡点扩展到平衡区间，共享车数量落到预定平衡区间，可视为达到平衡，这种定义法可减少平衡时间，减少旅行成本.

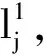
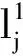
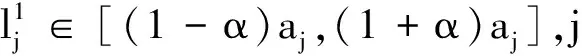
当α=0时，平衡间隔区间为平衡点，是平衡间隔区间的一个特例.显然，α的值不同会导致平衡区间的大小不同.一条访问路线的各站点库存情况如表1所列.假设站点j的目标库存为30，α=0.2.采用平衡间隔后，平衡区间为[24,36]，则1、2、4、14站的库存处于平衡区间.

表1 站点库存情况

另外每个站点既需要足够的共享车以满足用户的租赁需求，又需要足够的空位来满足用户归还共享车的需求.因此，站点服务功能包括共享车租赁功能和归还功能.

1.2 再平衡效益衡量函数

Li[9]考虑未满足需求的惩罚函数.本文考虑将未满足需求的惩罚转换成满足需求的程度，表现为共享车租赁功能和归还功能的使用程度.

站点可分为3个间隔：(0,(1-α)aj]，((1-α)aj,(1+α)aj]，((1+α)aj,Hj].在左侧间隔内，当车站为空时，共享车不能租用，所有插槽都可返回，因此租赁能力为0，返还能力是1.随着共享车数量的增加，租赁能力也增加了，也有足够的空地来满足用户的退货请求，返还能力仍然是1.当共享车的数量增加到(1-α)aj时，有足够的共享车出租，租赁能力增加到1，返还能力仍然是1.左侧间隔内站点服务能力取决于租赁能力.在中间间隔，即平衡间隔内，车站有足够的共享车和足够的空地，所以站点的服务能力保持在1.在右侧的区间内，如果共享车增加，租赁能力保持在1，但空置空间越来越少，返回能力减少.当车站车满了，租赁能力仍然为1，返回能力变为0.右侧间隔内的站点服务能力取决于返回能力.

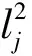
再平衡效益函数在三个间隔(0,(1-α)aj]、((1-α)aj,(1+α)aj]、((1+α)aj,Hj]上的值越大，说明需求满足的程度越高，站点服务能力越好.

1.3 模型的建立

本文重点考虑访问站点的旅程和站点服务能力，建立双目标函数.该函数定义在完全图G=(V,A)上，A={(i,j)}是路线弧的集合，dij是顶点i和顶点j之间的距离.如果车辆从站点i行驶到站点j，二元决策变量xij=1；否则xij=0，决策变量xij是0,1整数变量.变量yij表示在弧线(i,j)∈A上流动的共享车的数量，yij也是整数变量.

本文在平衡弹性区间的基础上建立模型：

(1)

(2)

(1)是行驶路线最小化；(2)是再平衡效益指标函数最大化.变量满足如下约束条件：

(3)

该条件确保每个站点必须恰好访问一次.

(4)

规定进入和离开j站的流量之间的差等于再平衡需求.

(5)

该条件确保一个站点只进行交付或者收集这两种操作之一.

(6)

该条件确保在站点收集的车辆不能超过车辆的剩余量.

(7)

该条件确保交付到j站的车辆不能超过再平衡操作车辆持有的库存.

下面将(1)、(2)的可行区域进行松驰，形成两个规划问题：

(8)

(9)

显然所有路径之和是(8)的上界，无平衡操作是(8)的下界，则

是需求满足程度的指标，每个站点的平衡满足程度指标：

达到最大，使整体满足程度变大，则

记

与单目标模型相比，多目标模型可以生成一组非支配最优解，根据不同的实际情况选择合适的方案.

2 粒子群-禁忌搜索算法

本文采用粒子群-禁忌搜索算法(TS-PSO)进行布局优化，并在粒子群迭代过程中引入3种变异粒子，增加粒子群的多样性，避免陷入局部最优.

假设在二维搜索空间中，有m个粒子组成一群体，第i个粒子在二维空间中的位置表示为xi=(xi1,xi2)，第i个粒子经历过的最好位置(有最好适应度)记为Pi=(pi1,pi2)，每个粒子的飞行速度为Vi=(vi1,vi2),i=1,2,…，m.在整个群体中，所有粒子经历过的最好位置为Pg=(pg1,pg2)，每一代粒子根据下面公式更新自己的速度和位置：

vid=wvid+c1r1(pid-xid)+c2r2(pgd-xid)，

(10)

xid=xid+vid，

(11)

其中：w为惯性权重；c1和c2为学习因子；r1和r2是[0,1]之间的随机数.

2.1 领域变异操作

为了增加粒子的多样性，同时使搜索范围变大，粒子随机执行3种结构的变异，具体如下：

(1)随机选取一个位置，将其从原位置移开，插入到另一个随机位置；

(2)随机选择两个位置，交换位置；

(3)随机选择几个位置，按逆序排列.粒子变异操作后，如果新粒子优于原粒子，则新粒子将取代原粒子;如果原粒子支配新粒子，则新粒子将被丢弃.否则，如果这两个粒子之间没有优势关系，则随机选择其中一个.通过改变站点的排列，可以确定一条新的车辆路线.为了生成初始解种群，可以采用上述随机变异的方式形成不同的粒子.

2.2 改进算法设计

由于粒子群算法具有局部搜索能力弱，容易陷入局部最优等缺点，本文对粒子群算法进行改进，提出一种粒子群-禁忌搜索算法(TS-PSO).

TS-PSO算法流程如下：

(1)初始化算法参数，随机生成粒子的初始位置和速度；

(2)计算每个粒子的目标值f1*,f2*；

(3)对每个粒子，比较目标值f1*,f2*和目前的最优f1(pbest),f2(pbest)，如果f1*f2(pbest)，则更新目前最优pbest=pnow，T=N(pbest)；

(4)对每个粒子，判断是否符合变异条件，如果符合进入步骤5；

(5)对pbest(j)进行变异操作，如果变异后的粒子目标函数值更优，则保留变异，否则取消当前变异；

(6)将所有粒子的最优值中最优的个体存储在全局最优gbest中；

(7)更新每个粒子的位置和速度；

(8)进行边界条件处理；

(9)判断是否满足粒子群迭代终止条件，若是，则结束粒子群算法迭代进入下一步；否则返回步骤2；

(10)将得到的最佳微粒解码，进行禁忌搜索；

(11)禁忌搜索操作结束，输出结果.

3 收敛性分析

粒子群-禁忌搜索算法是在二维搜索空间中进行，可选择10块平面区域，每块区域设定800 m×800 m，随机选择一块研究区域，在区域内选择潜在站点.潜在站点的选择基于以下规则:①站点应位于距离重要交通枢纽(如火车站、公交终点站和地铁站)和主要路口300～500m处；②站点应靠近较大的居住区、机关、企业、商业区、学校、医院、旅游景点等；③站点应避免直接进入繁忙的机动车道和十字路口.基于上面原则选定60个潜在的共享车站点和一个仓库.容量为Q的平衡车从仓库出发开始访问站点，一条访问路线，即为目标函数的一条典型的解或者一个粒子.访问站点的同时也对站点进行再平衡.

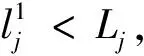
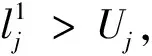
算法流程如下：

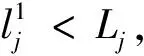
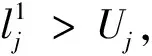
表1是包含15个站点的访问路线和站点库存.若共享车数量在平衡间隔内，则该站点可以视为处于平衡状态，不需要重新平衡.沿用2.1的假设，站点j的目标库存为30，α=0.2，平衡区间为[24,36].对于不平衡的站点用平衡车再平衡，具体平衡结果如表2所列.访问路线如表2的第一行.其中“+”表示提货再平衡需求，“-”表示配送再平衡需求.

通过再平衡，可使其余站点达到平衡.从表2可以看出10、12站未达到目标库存，但已经在平衡间隔内，再平衡程度相对满意，这也体现了平衡间隔的优势.

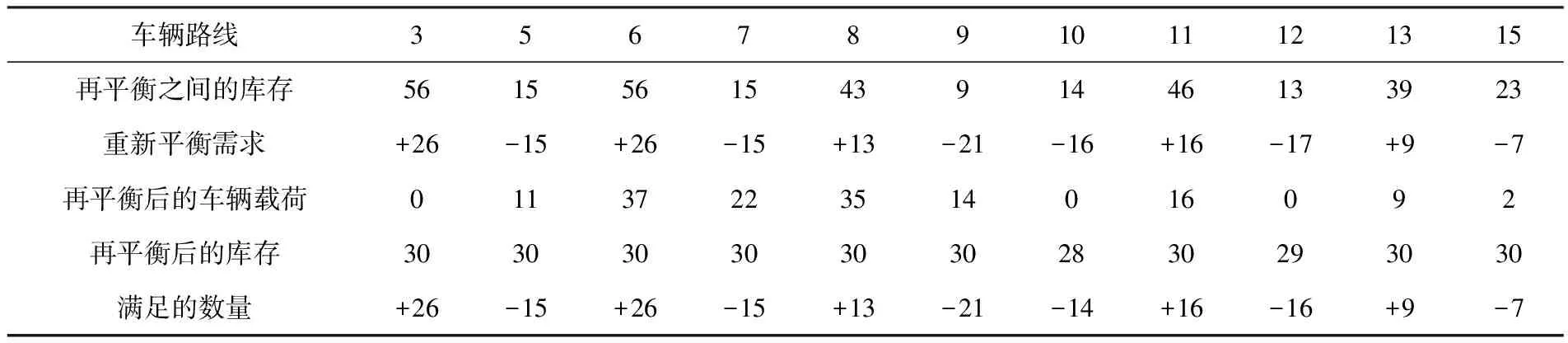
表2 初始解决方案的一个示例

4 结语

本文引入平衡区间和再平衡效用函数，建立双目标函数，提出粒子群-禁忌搜索算法，加入三种变异粒子，改进了算法，使得平衡次数和时间变少.由于α的不同会影响平衡区间及目标函数，下一步会探讨不同的参数值对目标函数的影响.