台风强度模拟的海温目标观测研究

姚佳伟 段晚锁

1 中国科学院大气物理研究所大气科学和地球流体力学数值模拟国家重点实验室，北京 100029

2 中国科学院大学地球与行星科学学院，北京 100049

1 引言

热带气旋（Tropical Cyclone; TC）是破坏性最大的天气系统之一，常常给沿海国家和地区的人民生命财产安全造成巨大损失（Peduzzi et al., 2012），因此，TC 的预报具有重要意义。随着卫星、雷达等观测资料的完善、资料同化技术的改进以及数值模式质量的提高，TC 路径预报技巧显著提高（Rogers et al., 2006）。对于TC 强度，因为其受到不同尺度因子相互作用的影响（Montgomery and Smith, 2017），机理相对更复杂，从而导致TC 强度的预报具有很大挑战性。

已有研究表明，TC 强度预报的不确定性受到多种误差来源的影响。Emanuel and Zhang（2016）研究指出，在TC 发展的初始阶段，初始涡旋误差对TC 强度预报误差起主要作用；而在随后阶段，路径及垂直风切变误差对TC 强度预报误差影响较大。Nasrollahi et al.（2012）研究表明，参数化过程（如积云对流参数化）的不确定性对TC 强度预报模拟也有重要的影响（亦见Parker et al., 2017）。事实上，前人的工作主要考虑了大气的初始场不确定性或参数不确定性对TC 强度预报误差的影响，而很少考虑海温误差的影响，甚至认为海表温度（SST）对TC 强度影响较小（Evans, 1993；Parker et al., 2017）。然而，大量的观测和理论研究表明，TC 和海洋之间存在强烈的相互作用。如Emanuel（1988）提出的MPI（Maximum Potential Intensity）理论将TC 看作一个热机，TC 最大的可能强度（MPI）取决于下垫面的SST 与对流层出流温度，而Demaria and Kaplan（1994）以及Schade（2000）研究表明，当海温大于24°C 时，对流层出流温度与SST 存在线性关系。综合两者可知，TC 的MPI是由SST 所决定的。Emanuel et al.（1994）提出WISHE（Wind Induced Surface Heat Exchange）机制，进一步表明了SST 对TC 强度发展具有重要影响。另外，由于TC 对海洋的抽吸和搅拌作用，伴随着SST 的冷却现象（Price, 1981; Shay et al.,1992; Schade and Emanuel, 1999; Srinivas et al.,2016），台风内部向上的热通量会被抑制，进而抑制TC 强度增强，从而使得实际观测或者模拟的TC 强度低于MPI 理论的结果。特别地，Torn（2016）研究指出，SST 不确定性对TC 强度预报的影响大于模式参数不确定性的影响，尤其在预报或模拟的后期阶段，SST 不确定性对强度预报的影响与大气不确定性的影响是相当的。

目前大部分TC 业务预报模式采用固定的海温条件，这样就忽略了SST 负反馈过程的作用（Winterbottom et al., 2012; Sun et al., 2014）；即使采用耦合模式，由于模式本身的不确定性，或者耦合频率较低等问题，耦合模式模拟的SST 也会存在误差（Davis et al., 2008; Scoccimarro et al., 2017）。所以，SST 误差在TC 预报或模拟中是不可避免的。从以上讨论可以看出，这里的SST 误差不仅可以理解为由于海温观测的不准确或者耦合模式TC 与海洋相互作用描述不够完美而导致的。

基于上述讨论，我们自然会问：如何提高SST 强迫场的准确性或者与TC 强度相关的TC—海洋相互作用的模拟水平，进而提高台风强度的预报水平？毫无疑问，增加观测是提高SST 强迫场准确性的有效途径。同时，为了在耦合模式中准确刻画TC—海洋的相互作用，模式研究者也是基于大量的观测事实去构建能够反映TC—海洋相互作用的优化模型，从而改进海温的模拟能力。显然，两个方面都需要增加观测来实现。那么，为了有效提高TC 强度的模拟水平，我们究竟应该在哪个区域或者台风演变的哪个阶段对SST 优先进行观测呢？该问题实际上涉及到始于1990s 的“目标观测”新策略（Snyder, 1996; Mu, 2013）。目标观测是作为改善初始场问题被首先提出的，主要思路如下：为了提高某一天气、气候事件在未来时刻（验证时刻）在所关心的区域（验证区域）的预报技巧，而在此时刻之前的某一时刻（目标时刻），在一些关键区域（亦称“敏感区”）增加额外观测，通过同化这些额外观测而形成一个更加合适的初始场，从而最大限度地减小验证区域的预报误差（详见Mu,2013）。

如上所述，目标观测被用于减小初始误差（Petersen and Thorpe, 2007; Wu et al., 2007; Buizza et al., 2007; Qin and Mu, 2012; Duan and Hu, 2016）。为了探究外强迫的不确定性对模拟技巧的影响，Wen and Duan （2019）将目标观测的思想拓展到减小外强迫误差，分析了究竟哪个区域的观测能够有效地减小强迫误差的影响，而提高数值模式模拟技巧。在本研究中，我们拟从SST 强迫对TC 强度模拟的影响的角度探讨TC 强度模拟的不确定性。所以，我们采用Wen and Duan（2019）提出的外强迫目标观测思路，即探讨对TC 强度模拟影响最大的SST 强迫目标观测。

目标观测的关键是确定目标观测敏感区。根据Wen and Duan（2019）的思路，若要确定外强迫目标观测敏感区，应首先确定对TC 强度模拟不确定性影响最大的SST 外强迫误差。事实上，Yao et al.（2021）已经利用WRF 模式探讨了SST 强迫不确定性对西北太平洋12 个TC 强度模拟的影响，并获得了对TC 强度影响最大的海温强迫误差模态，即具有非线性强迫奇异向量（NFSV）空间结构的SST 强迫误差。NFSV 是指能够导致最大预报误差或模拟误差的外强迫误差（Duan and Zhou, 2013）。该方法已被成功应用于台风、厄尔尼诺和源区黑潮等高影响天气气候事件的可预报性研究中（Duan and Zhao, 2015; Wen and Duan, 2019; Qin et al.,2020），获得了有意义的结果。不同于初始场的目标观测，强迫场的目标观测策略既涉及到在哪个区域进行目标观测，又需要考虑在哪个时段进行目标观测能取得最优的效果。如上所述，Yao et al.（2021）已经得到了对TC 强度模拟不确定性影响最大的NFSV 型SST 强迫误差。NFSV 型SST 强迫误差是定常的，它可以理解为对台风强度模拟具有最大影响的SST 强迫的系统性偏差，也可理解为模拟时段内对TC 强度影响最大的SST 强迫误差的均值。另外，定常的NFSV 型SST 强迫误差，使得TC 强度模拟在每个时刻受到相同大小和相同空间分布的海温强迫误差的影响，这便于我们在相同条件下比较TC 强度模拟不确定性对不同时段SST 强迫误差的敏感依赖性，从而获得SST 强迫的最优目标观测时段。因此，在上述研究的基础上，本文针对台风强度模拟的海温目标观测，提出以下问题：（1）如何根据NFSV 型SST 强迫误差确定TC 强度模拟在海洋上的SST 目标观测布局以及最优观测时段？（2）最优观测时段的目标观测及其观测布局能在多大程度上改进TC 强度的模拟水平？

2 WRF 模式及方法

本文使用WRF-ARW（The Weather Research and Forecasting Model，the Advanced Research WRF）3.8.1 版本。WRF 模式是中尺度非静力可压缩的大气动力模式，常常用于TC 强度和路径的预报研究。对于WRF 模式，本文采用如下参数化过程：（1）云微物理过程，采用Lin et al.（1983）提出的参数化方案；（2）积云对流过程，采用Kain-Fritsch 方案（Kain, 2004）；（3）长、短波辐射参数化过程，分别采用Rapid Radiative Transfer Model（RRTM;Mlawer et al., 1997）和Dudhia 参数化方案（Dudhia,1989）；（4）边界层参数化过程，采用Yonsei University 的参数化方案（Hong et al., 2006）。为了考虑海洋对TC 强度模拟的影响，该研究引入了随时间变化的海温强迫场，即通过每6 小时输入观测的SST 来强迫WRF 模式；在差分网格分辨率上，水平网格采用30 km×30 km，设置垂直方向24 层，而顶层为50 hPa；模式的时间积分步长为90 s，每个台风模拟积分时长为5 天，每3 小时输出一次结果，共40 个输出时次。模式初始化中用到的大气资料（包括风、温、压、湿、降水等）来自于美国国家大气环境研究中心（the National Centers for Environmental Prediction，NCEP）的FNL 再分析数据，其精度为1°×1°；地形高度也是采用NCEP提供的高精度地形数据；观测的海温资料来自于NCEP 的实时海温再分析，精度为0.083°×0.083°。因为NCEP 的海温再分析是逐日资料，不符合模式积分步长的时间，所以本研究将逐日的海温资料进行了时间上的插值，得到了步长为6 小时的海温强迫场，然后用于WRF 模式强迫大气。

该研究仍然采用Yao et al.（2021）所研究的12 个TC 个例。这些TC 个例的移动路径受SST 强迫误差的影响很小，从而排除了移动路径的变化对TC 强度的影响。基于Yao et al.（2021）揭示的NFSV 型SST 强迫误差，本文采用观测系统模拟试验（OSSE）确定TC 强度模拟的SST 目标观测布局及最优观测时段。所谓OSSE，即首先将在模式合理设置下的一次数值模拟作为“真实”场（Nature Run），并基于该“真实”场的格点构建模拟观测资料，然后评估加入模拟观测资料后的预报与“真实”场的拟合程度，以此分析观测系统的观测对数值模拟效果改善的程度（Privé et al.,2021）。该方法不考虑模式误差的影响，它使用模拟观测，将其同化到模式初始场，避免了因为缺少观测而无法提供模式初始场进行模拟研究的局限性，该方法可为未来的观测提供合理有效的建议（Arnold and Dey, 1986）。具体到该研究考虑的SST 外强迫场，采用的OSSE 步骤如下：（1）对所研究的TC，将其演变过程中每6 小时所对应的再分析SST 场作为“真实”的随时间变化的SST，应用于WRF 的强迫场；采用FNL 初始分析场作为大气初始场，积分WRF 120 小时，作为“Nature Run”。（2）根据Yao et al.（2021）研究中的198 个海温强迫扰动试验结果，遴选出对TC 强度有较大影响的20 个SST 强迫误差（以SST 强迫误差引起的TC 强度在整个模拟区间的总误差超过300 hPa来衡量），将其叠加到“真实”的SST 强迫场，并l 积分模式120 小时，作为“Control Run”。（3）根据NFSV 型SST 强迫误差确定目标观测布局的网格点。（4）在模拟过程中的各个时刻的观测网格点上构造模拟观测，并将其同化到“Control Run”的SST 强迫场，得到更新的SST 强迫分析场。（5）用更新的SST 强迫分析场替换步骤（1）中“真实”的SST 强迫场，积分模式120 小时，将得到的模拟结果记为“Sensitive Run”，并与“Control Run”比较，考察目标观测在提高台风强度模拟技巧中的有效性。根据试验目的的差异，该研究将OSSEs 分为两类，OSSE-S 和OSSE-T。在OSSE-S 中将进行4 组OSSEs，每组试验的区别在于第三步骤不同，详见表1；在OSSE-T 中将进行2 组OSSEs，每组试验区别在于第五步骤不同，详见表2。

表1 OSSE-S 第三步设置说明Table 1 Settings of Step 3 of OSSE-S

表2 OSSE-T 第五步设置说明Table 2 Settings of Step 5 of OSSE-T

为评估目标观测对TC 强度模拟的改善程度（ η），采用公式（1）作为度量：

其中，ECtrl为“Control Run”相对于“Nature Run”的TC 强度误差，ESen为“Sensitive Run”相对于“Nature Run”的TC 强度误差。TC 强度误差E采用公式（2）计算：

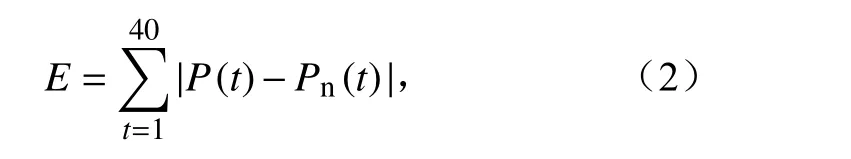
其中，Pn为“Nature Run”的TC 强度，P为“Sensitive Run”或“Control Run”的TC 强度，这里的TC 强度采用最小海平面气压度量。

该研究采用最优差值（Optimal Interpolation，OI）资料同化方法同化SST 模拟观测。最优插值方法的同化公式如下：

其中，Xa是分析场，Xb为背景场，y是观测值；H为从背景场到观测场的映射矩阵，即观测算子；K为增益矩阵，如公式（4）所示：

这里的B为背景误差协方差矩阵，O为观测误差协方差矩阵；下面的公式（5）给出的是权重系数wi,j（即第j个模式格点到第i个观测点的权重系数）的计算公式，采用了距离平方反比：

3 最优目标观测布局和最优观测时间的确定

对于强迫场的目标观测，其关键既要确定目标观测敏感区，又要识别最优的目标观测时段。根据Yao et al.（2021）的结论，NFSV 型SST 强迫误差对TC 强度模拟不确定性具有最大影响，且NFSV 误差的大值区主要位于TC 的移动路径上，发生在TC 快速增强阶段（如图1 所示）。该结论意味着，NFSV 型SST 强迫误差导致TC 强度最大的模拟误差，代表了TC 强度模拟的最敏感的SST误差，而误差的大值区则表明了TC 强度模拟对该区域以及对应时段的SST 误差最敏感。如果在该区域和相应时段增加额外观测，改善SST 强迫场，则TC 强度的模拟水平可能会明显改善。所以，NFSV 型SST 强迫误差的大值区可能代表了TC 强度模拟的海温目标观测敏感区，其所在阶段也可能代表了TC 强度模拟对海温目标观测的敏感阶段。因此，我们可以根据NFSV 型SST 强迫误差的大值区来确定TC 强度模拟的SST 目标观测布局以及最优观测时段。

3.1 最优目标观测布局的确定

理论上，在NFSV 型SST 强迫误差场中，网格点上误差越大意味着TC 强度模拟对该格点误差越敏感，而目标观测就越应该布置在该格点的位置。为了确定能够有效提高TC 强度模拟水平的目标观测的最优观测布局，我们首先进行两组OSSE 试验，即OSSE-S-I 和OSSE-S-II，并以图1 中TC 个例Soulik 为例进行介绍。

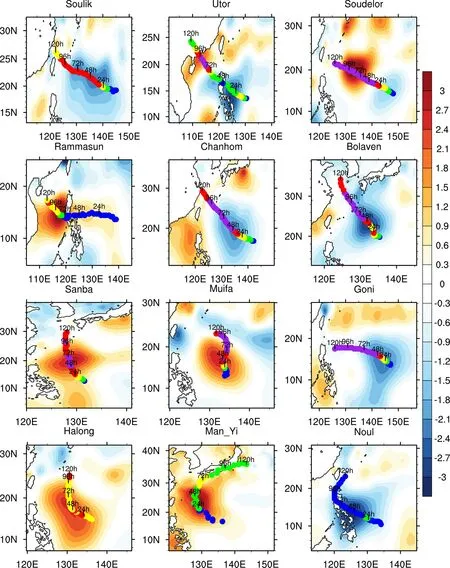
图1 12 个TC 个例的非线性强迫奇异向量（NFSV）型SST 强迫误差结构（阴影，单位：K）。其中点为TC 的路径；蓝色、绿色、黄色、红色、紫色的点分别代表模拟TC 强度大小在980～1000 hPa、970～980 hPa、960～970 hPa、950～960 hPa 和900～950 hPa 的范围内Fig. 1 Patterns of Nonlinear Forcing Singular Vector (NFSV)-type SST forcing errors (shaded, units: K) of the selected 12 TC cases. The dots represent the tracks of TCs and the blue, green, yellow, red, and purple dots indicate the simulated TC intensity within 980-1000 hPa, 970-980 hPa,960-970 hPa, 950-960 hPa and 900-950 hPa

OSSE 试验的步骤如第二节所示，OSSE-S-I和OSSE -S-II 的差别在于第三步，即目标观测的布局不同。OSSE-S-I 的第三步是根据NFSV 型SST 强迫误差大小，依次在误差大小排名前20、40、60、···、120、140、···、240 的格点分别构建模拟观测。当构建的观测数低于120（即选取的格点数低于120）时，目标观测敏感区主要分布于（20°N～26°N，132°E～140°E）（记为区域A）；当选取的格点数超过120 时，在（24°N，130°E）附近出现新的目标观测区（如图2 所示）。

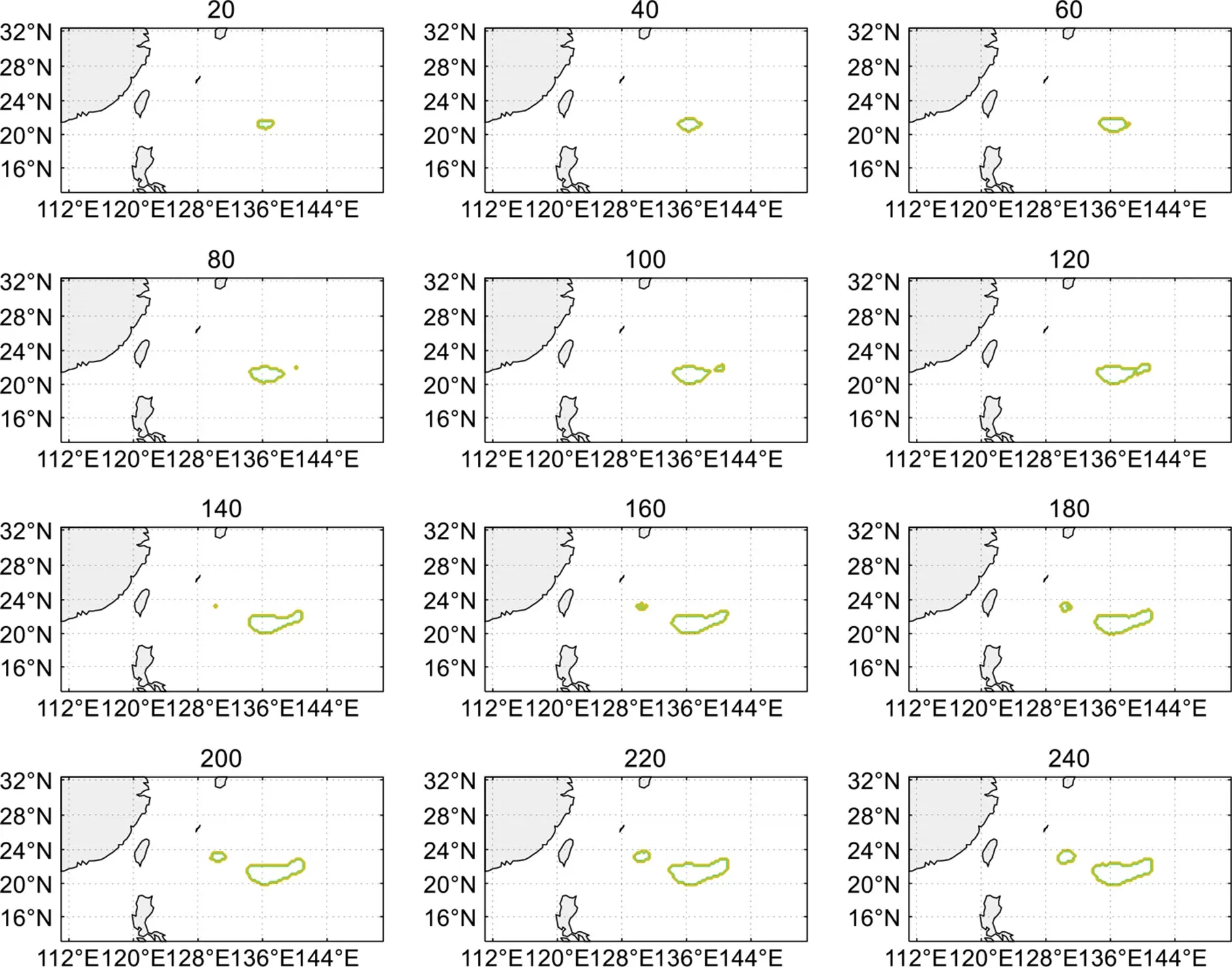
图2 Soulik 个例的NFSV 型SST 强迫误差中前20、40、···、240 个大值点所构成的敏感区范围Fig. 2 Regions of the sensitive area identified by the leading 20, 40, ···, 240 large values of the NFSV-type SST forcing error for TC Soulik

这里的模拟观测是在“真实”的SST 上叠加服从N（0，0.1）分布的随机误差而构造的。选取上述不同数目的模拟观测，将其同化到“Control Run”的SST 强迫场，利用更新的SST 强迫场积分WRF，考察TC 强度模拟误差的变化情况。结果表明，如果仅同化NFSV 型SST 强迫误差前20个大值点的模拟观测时，即可使得TC 强度模拟误差减小67%（如图3 所示），而且随着同化模拟观测数的进一步增加，TC 强度模拟技巧的改善程度逐渐增加，并在同化的模拟观测数达到120 时，TC 强度模拟改善程度达到峰值，模拟误差减小达到76.8%。然而，当目标观测敏感区范围进一步扩大，同化的模拟观测数进一步增加时，TC 强度模拟的改善程度会出现一定程度的下降（见图3）。

图4 给出了同化不同数量模拟观测后，SST 强迫场的改善情况。从图中可以看出，当模拟观测数少于120 时，SST 强迫误差主要减小的是区域A的误差，且SST 误差减小幅度随着模拟观测数的增加而增大（如图5 所示）；而当模拟观测数超过120 以后，SST 强迫误差减小的主要区域转移到区域B（即20°N～26°N，128°E～132°E ；图4），且区域A 的SST 误差的改善程度倾向于随着观测数的增加达到饱和后降低（图5）。这种SST 强迫误差改善程度的变化规律恰恰对应了上述随着同化的模拟观测数的增加，TC 强度模拟改善程度达到饱和，然后转而减小的变化规律。另外，我们注意到区域A 与NFSV 型SST 强迫误差的大值区有较多重合，而区域B 并未位于NFSV 型SST 强迫误差的大值区（图4）。综合这些结果，我们可以推断，区域A，即NFSV 型SST 强迫误差值更大的区域，代表了TC 强度模拟的目标观测敏感区，该区域SST 强迫误差的减小能有效改善TC 强度的模拟水平，所以SST 强迫的目标观测应优先布放在NFSV 型SST 强迫误差的前120 个格点，即区域A。

图4 同化敏感区范围内的观测后，SST 强迫场的变化情况（填色，单位：K）。其中红色实线框出的范围表示对应的目标观测敏感区Fig. 4 Change of SST (shaded, units: K) forcing field after assimilating the observations in the sensitive area to different extents. The red line represents the extent of the corresponding sensitive area of the target observations

在OSSE-S-I 试验中，我们对敏感区内的每个格点都构建了模拟观测，但从图5 的结果可以发现，当构建的模拟观测数从20 增加至120 的过程中，同化增加的模拟观测使得区域A 减小的SST 误差从1.3 K 增加到1.5 K。由此可以看出，在模拟观测数20 的基础上，进一步增加的模拟观测使得SST 误差减小的收益是减小的。那么，这种事实是否意味着，我们并不需要对敏感区内所有的格点进行观测，便可以在TC 强度模拟技巧的改善中获得与所有格点进行观测相当的效果呢？为回答该问题，本文设计了OSSE-S-II 试验。OSSE-S-II 的各个试验步骤与OSSE-S-I 基本相同，只在第三步骤略有不同，不同之处在于OSSE-S-II 在该步骤获得的目标观测布局是在OSSE-S-I 的目标观测布局基础上，分别选取不同间隔（即30 km、60 km、90 km、120 km）的观测进行同化。不同间隔对应了敏感区内不同的观测数（如表3 所示）。

表3 OSSE-II 中敏感区内不同观测布局的观测数Table 3 Numbers of observations with different intervals in the sensitive area of OSSE-II

图5 OSSE-S-I 中，同化不同范围敏感区内的模拟观测后，区域A 所减小的绝对SST 误差大小（单位：K）Fig. 5 Absolute reduced SST errors in region A after assimilating the observations in sensitive areas to a different extent in OSSE-S-I (units: K)

图6 给出的是不同观测间隔下，同化敏感区内SST 模拟观测对TC 强度模拟的改善情况。从图中可以看出，在敏感区内所有格点上进行观测，对TC 强度模拟改善程度最高，但当观测数达到120 时，每个观测的平均收益是很低的。但当我们以90 km 为间隔构建模拟观测时，只需要12 个观测点，便能够使TC 强度模拟的改善效果达到75%，这仅仅略低于在敏感区所有格点进行观测后的改善效果76.8%，但观测数却减少了90%。虽然进一步增大观测间隔至120 km，观测数仅有7 个，而且每个观测对TC 强度模拟改善的平均收益是最高的，但是对TC 强度的模拟改进程度却降低至73%。所以，如果综合考虑TC 强度模拟的改善效果及观测的成本，选取90 km 作为观测间隔在敏感区内构建观测网可能是更优策略。

图6 OSSE-S-II 的模拟结果。同化目标观测敏感区不同观测间隔的观测后，TC 强度模拟的改善程度Fig. 6 Results of OSSE-S-II. The improvement rate in the TC intensity simulation after assimilating observations with different intervals in the sensitive area

3.2 最优观测时段的确定

在实际业务预报中，海温强迫是持续作用在模式场上，这意味着在各个时刻都存在海温强迫误差对TC 强度的负面影响。然而，根据Yao et al.（2021）的结果，TC 强度对海温强度误差存在时间上的敏感依赖性，并且NFSV 型SST 强迫误差的大值区对应了TC 强度对海温误差最敏感的阶段。因此，我们根据NFSV 型SST 强迫误差确定目标观测的最优时间段。为此，基于OSSE-S-I 和OSSE-S-II 的结果，我们设计了OSSE-T-I 试验，并以Soulik 个例进行说明。

OSSE-T-I 的步骤亦如第二节所述，但其第三步采用OSSE-S 试验中所确定的最优观测布局，第五步只在第0 h，6 h，12 h，···，114 h 替换步骤（1）中对应时刻“真实”的SST 强迫场，并积分模式120 小时。由此，我们可以根据同化后对TC强度模拟改善程度的差异确定出最优观测时段。试验结果如图7 所示。结果表明，尽管仅在单个时刻进行目标观测改善SST 强迫场，对TC 强度模拟的改善效果不大，但是从图中可以明显看出，在18～54 h 这个阶段进行目标观测对TC 强度的模拟具有更为明显的改善。对比NFSV 型SST 强迫误差的结构，我们很容易发现，这个阶段恰好对应于NFSV 型SST 强迫误差的大值区所对应的TC 时段，一般处于台风快速增强阶段。由此，当我们进行目标观测时，我们可以根据NFSV 型SST 强迫误差大值区所对应的TC 快速增强阶段确定最优观测时间。

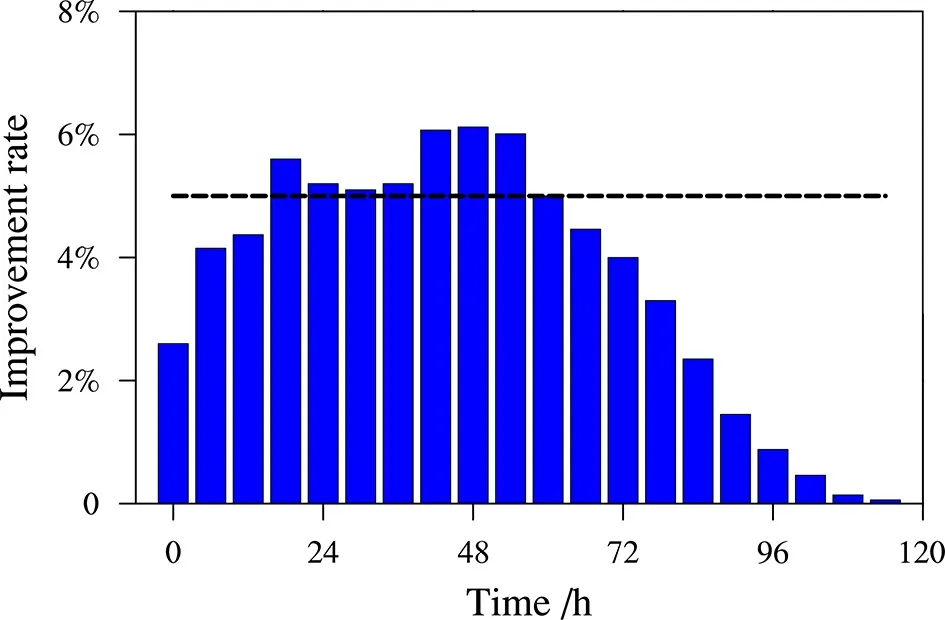
图7 OSSE-T-I 的模拟结果。在单个时刻同化敏感区内的模拟观测对TC 强度模拟的改善情况。虚线为改善程度达5%的参考线Fig. 7 Result of OSSE-T-I. The improvement rate of the simulation of the TC intensity after assimilating observations in the sensitive region only once at the corresponding time. The dashed line is the reference line of the 5% improvement

对于图1 中的其他个例，试验结果也都表明，当模拟的观测数选取在NFSV 型SST 强迫误差的前120 个格点，且以90 km 间隔布放观测时，同化这些观测会对TC 强度的模拟有更好的改善且最大程度节省观测成本；同时，NFSV 型SST 强迫误差大值区所对应的TC 阶段亦与最优目标观测时段一致，这里不再赘述。综上所述，根据NFSV 型SST 强迫误差结构，通过OSSE-S-I 及OSSE-S-II确定了TC 强度模拟的SST 目标观测敏感区以及敏感区内的观测布局，即选取NFSV 型SST 强迫误差中前120 个误差大值点作为目标观测敏感区，并在敏感区中以90 km 为间隔布置观测；通过OSSET-I 确定了TC 强度模拟的SST 目标观测的优先观测时段，即NFSV 型SST 强迫误差的大值区对应台风快速增强阶段。

4 目标观测的有效性

上节讨论了在NFSV 型SST 强迫敏感区内如何以及何时布放观测能够最大程度提高TC 强度模拟技巧且节省观测成本。本节将验证敏感区内进行目标观测的有效性。因为第三节确定的目标观测最优布局主要覆盖了一个局地区域，所以我们首先要验证的是：是否该局地区域的目标观测较其他局地区域的加密观测对TC 强度模拟的改善更显著？另外，与覆盖范围更大的非敏感区相比，在敏感区进行相同数目的目标观测是否对TC 强度模拟的改善也更加有效？最后，在上述揭示的优先观测时间（或敏感性时间段）和非敏感时间段进行目标观测是否对TC 强度模拟的改进有显著差别？为回答这些问题，该研究设计了OSSE-S-III、OSSE-S-IV和OSSE-T-II。

OSSE-S-III 与OSSE-S-I 和-S-II 的不同亦在于OSSE 试验的第三步。OSSE-S-III 的第三步是在NFSV 型目标观测敏感区外（或非敏感区）随机选取20 个与敏感区范围相当的局地区域，且在每个区域内以90 km 为间隔布置16 个观测，然后对比同化非敏感区局地区域的观测和敏感区域的观测对TC 强度模拟的改善程度。图1 中12 个TC 个例的OSSE-S-I 模拟结果如图8 所示。由图可以看出，同化非敏感区的局地观测对TC 强度模拟的改善有一定的提高，但都不会优于同化敏感区内目标观测的效果，而且随机选取的非敏感区局地观测区域越接近目标观测敏感区，同化SST 加密观测对TC 强度模拟改善程度越高。具体地，图9 统计了OSSES-III 中所有TC 个例非敏感区局地观测区域距目标观测敏感区的距离与TC 强度模拟改善程度的散点图。结果发现，两者的相关性达到-0.49，且通过了99%的显著性检验。考虑到不同个例的差异，该研究进一步考察了每个TC 个例中上述两者的相关性，发现大多数个例中上述相关性更高（如表4所示）。事实上，所有这些结果都强调，由NFSV型SST 强迫误差所确定的敏感区的目标观测对于提高台风强度的模拟水平是最有效的。

图8 OSSE-S-III 的模拟结果。红色（蓝色）柱为同化小范围的敏感区（非敏感区）内观测，对TC 强度模拟的改善情况。“Sen”表示敏感区内进行的OSSE，“I+数字”表示在非敏感区进行的OSSEFig. 8 Results of OSSE-S-III. The red (blue) bars represent the improvement rate of the TC intensity simulation after assimilating the observations in local sensitive (nonsensitive) areas. “Sen” represents the OSSE conducted in the sensitive area，while “I+Number”represents the OSSE conducted in nonsensitive area

图9 非敏感区的局地观测距敏感区的距离与TC 强度模拟改善程度的散点图和线性拟合曲线（红色实线）。图中的公式为拟合函数，R 代表相关系数，P 为显著性水平Fig. 9 Scatter and linear fitting line (the red solid line) between the distance of observations in the nonsensitive area relative to the sensitive area and the improvement of the TC intensity (The formula is the fitting function between the two variables. R and P is the correlation coefficient and the significant level respectively.)

表4 不同个例对应的非敏感区局地观测距敏感区的距离与TC 强度改善程度的相关系数（ R）Table 4 Correlation coefficients ( R) between the distance of observations in the nonsensitive area relative to the sensitive area and the improvement of TC intensity simulation

上述试验结果表明，对于在非敏感区内且与敏感区范围相当的局地区域增加观测，在敏感区内增加相同数目的观测能够更加有效提高TC 强度模拟水平。那么，如果在整个非敏感区覆盖的大范围增加观测，小范围敏感区的观测是否在TC 强度模拟的改善中仍具有优越性呢？OSSE-S-IV 可以回答这个问题。在OSSE-S-IV 中，OSSE 试验的第三步是在大范围的非敏感区中均匀选取与敏感区内相同的格点数构建模拟观测，然后对比敏感区局地小范围观测与非敏感区的大范围观测对TC 强度模拟的改善程度。图10 展示的是同化了敏感区与非敏感区大范围观测后，对模拟的TC 强度的改进情况对比（即OSSE-S-IV 的模拟结果）。可以看到，在相同的观测数的条件下，同化了敏感区的观测之后，对TC 强度的改善效果是优于同化了非敏感区的大范围观测后的TC 模拟改善效果。由此可见，在SST 目标观测敏感区内加密观测，对于提高TC 强度的模拟能力是有效且经济的。

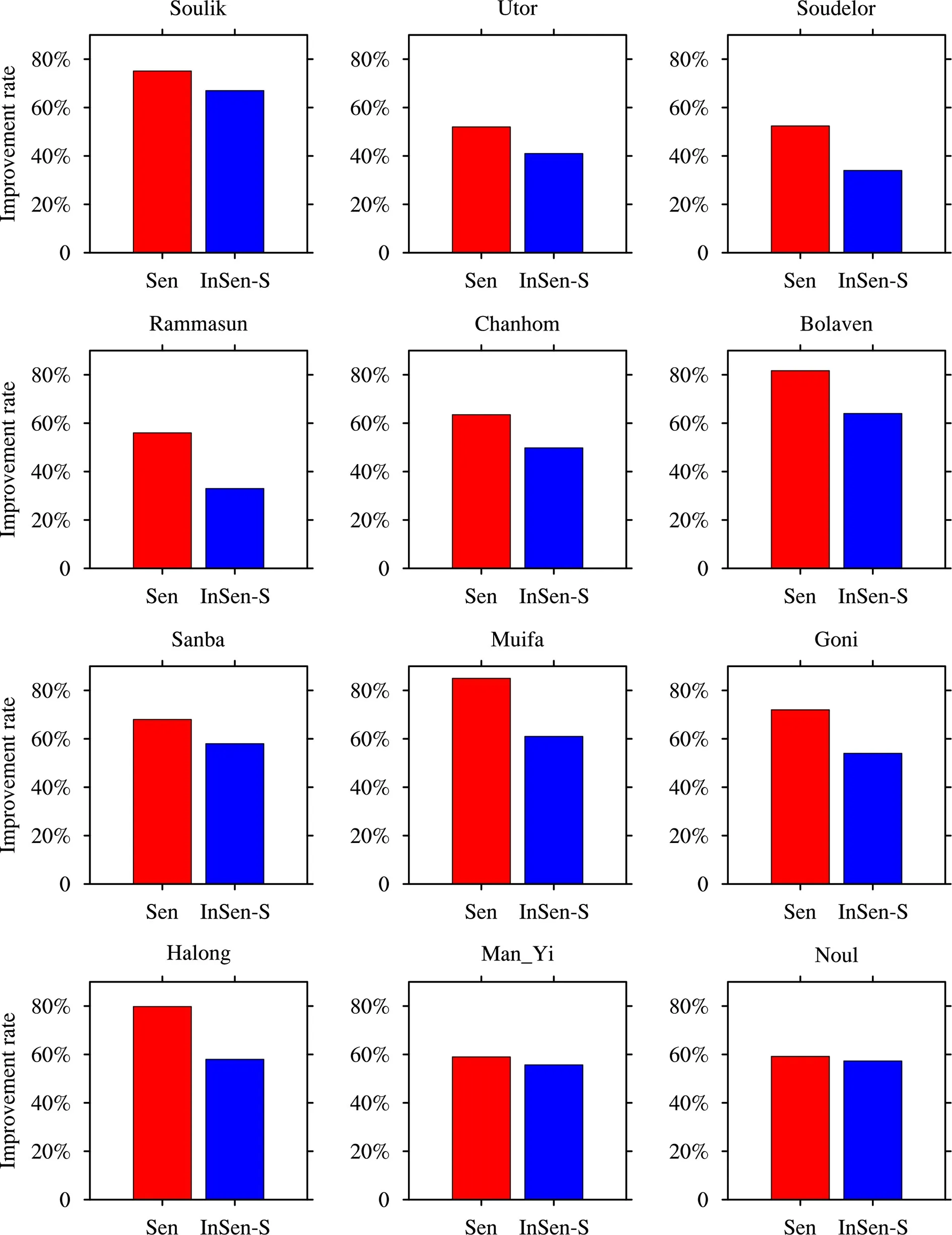
图10 OSSE-S-IV 的模拟结果。红色柱为同化敏感区内观测对TC 强度的改善程度；蓝色柱为同化非敏感区全场的观测对TC 强度模拟的改善程度。“Sen”代表在敏感区进行的OSSE，“InSen-S”表示在非敏感区全场进行的OSSEFig. 10 Results of OSSE-S-IV. The red bars represent the improvement of the TC intensity simulation after assimilating observations in the sensitive area. The blue bars represent the improvement of the TC intensity simulation after assimilating the same number of observations in the whole nonsensitive area. “Sen” represents the OSSE conducted in the sensitive area, and “InSen-S” indicated the OSSE conducted in the whole nonsensitive area

OSSE-T-II 的试验步骤与OSSE-T-I 类似，主要在于第五步存在区别。在OSSE-T-II 中，我们分别在敏感性时间段和非敏感性时间段将更新后的海温强迫场替换对应时间段“真实”的SST 强迫场。图11 展示的在敏感性时间段和非敏感性时间段进行目标观测后对TC 强度模拟的改进情况。由图可以看出，在敏感时间段进行目标观测改善SST 强迫场对TC 强度模拟的改善具有更大的作用。

图11 OSSE-T-II 的模拟结果。红色柱为同化敏感阶段的敏感区内观测对TC 强度的改善程度；蓝色柱为同化非敏感阶段的敏感区内观测对TC 强度模拟的改善程度。“Sen-T”代表在敏感区的敏感时段进行的OSSE，“InSen-T”表示在敏感区的非敏感时段进行的OSSEFig. 11 Results of OSSE-T-II. The red bars represent the improvement of the TC intensity simulation after assimilating observations in the sensitive area during the sensitive period. The blue bars represent the improvement of the TC intensity simulation after assimilating observations in the sensitive area during the nonsensitive period. “Sen-T” represents the OSSE conducted in the sensitive area during sensitive period, and “InSen-T” indicated the OSSE conducted in the sensitive area during nonsensitive period

综上所述，对比小范围的局地观测和大范围的全场观测，在NFSV 型SST 强迫误差的前120 个格点区域所确定的目标观测敏感区内，以适当的间隔布放观测并同化到海温强迫场，能够最大程度地改善TC 强度的模拟效果，尤以NFSV 型SST 强迫误差大值区所对应的TC 快速增强阶段的目标观测，对TC 强度模拟的改善最为明显。

5 总结和讨论

该研究基于Yao et al.（2021）揭示的对TC 强度模拟结果具有最大影响的NFSV 型SST 强迫误差，通过OSSE 试验确定了TC 强度模拟的SST 目标观测敏感区（即NFSV 型SST 强迫误差前120个大值点所覆盖的区域，该区域沿着TC 移动路径且主要位于TC 的快速增强阶段）以及目标观测的最优观测时段（即NFSV 型SST 强迫误差大值区对应的TC 快速增强阶段）。研究表明，在上述敏感区及敏感时间段中以90 km 为间隔布放“观测”并将其同化到WRF 的SST 强迫场，能够经济且有效地改善TC 强度的模拟技巧，可能代表了台风强度模拟的最优海温目标观测布局。

为验证目标观测敏感区的有效性，该研究设计了三组对比试验：同化敏感区内“观测”与同化非敏感区局地区域“观测”的对比；同化敏感区内“观测”与同化非敏感区全场“观测”的对比，以及同化敏感时间段的敏感区内“观测”与同化非敏感时间段的敏感区内“观测”的对比。结果表明，同化敏感区内“观测”对TC 强度模拟的改善效果要普遍要优于同化非敏感区局地区域“观测”的效果；而且当同化的非敏感区局地观测的区域越接近目标观测敏感区时，TC 强度模拟的改善程度越高；特别地，同化小范围敏感区内“观测”对TC 强度模拟的改善效果明显优于同化非敏感区大范围“观测”的效果。上述改善尤以NFSV 型SST 强迫误差大值区所对应的TC 快速增强阶段最为明显。所以，上述根据NFSV 型SST 强迫误差大值区所确定的最优目标观测布局及最优观测时段是有效的，该结果可为台风的实际外场观测（如无人潜艇目标观测）提供科学指导。

如前所述，该研究所选取的TC 个例的移动路径对海温强迫扰动并不敏感，所以，这里根据NFSV 型SST 强迫误差所确定的目标观测敏感区和最优观测时段，其目标观测可能不适用于TC 路径模拟的改善。另外，TC 强度预报水平的提高依赖于模式的模拟能力，该研究考虑通过目标观测策略提高SST 强迫场的准确性来改善台风强度的模拟，这对于具有SST 强迫场的非耦合模式模拟台风强度水平的提高具有重要意义。事实上，该研究的目标观测敏感区和敏感时段也对耦合模式模拟台风强度具有指示意义，即这些敏感性可以告诉模式开发者，如果优先使得耦合模式对上述敏感区和敏感时段的SST 有更好的模拟，那么耦合模式对TC 强度的模拟水平会得到有效改善，进而提高台风强度的预报水平。