非均匀应力场下隧道围岩弹塑性分析统一解

周 鹏， 刘永军

（1.三门峡市国道三一零南移项目建设管理有限公司，河南三门峡 472000；2.河南省交通科学技术研究院有限公司，郑州 450015）

在隧道工程实践中，隧道围岩应力及变形特征是评价围岩稳定性和隧道支护定量设计的理论基础［1-3］，受隧道开挖的影响围岩应力重分布，继而进入弹塑性变形状态［4］. 因此，展开隧道围岩的弹塑性分析具有重要的理论和工程实践意义［5］.

数值模拟作为隧道工程的重要解决手段之一，近20年来应用的越来越广泛，并且在围岩应力分析方面发挥了重要作用. 贾剑青［6］通过有限元方法分析深埋隧道的塑性区，并给出荷载松动圈范围. 李文华［7］优化了双侧壁导坑施工法，研究了大断面小净距双线隧道不同开挖工法下的围岩稳定性. 刘波［8］通过对三维隧道开挖进行模拟，基于位移和速率评价了围岩稳定性. 吕纬［9］通过分析含水砂层段的隧道稳定性，推导了不同施工方法开挖面极限支护应力表达式，并采用数值模拟分析了不同工况下的隧道稳定性，验证了地下水对隧道稳定性的影响. 上述研究采用有限元软件研究了隧道围岩应力及稳定性，积极地拓展了隧道围岩弹塑性分析方法.

现阶段，大多数学者采用M-C强度理论、H-B强度理论或D-P强度理论对隧道围岩进行弹塑性分析［10-13］.王明斌和李术才［14］基于M-C强度理论，推导出第一主应力分别为径向应力和环向应力时的隧道围岩全场弹塑性解答. 蒋斌松等［15］采用M-C强度理论和非关联流动法则，建立了符合变形协调条件的隧道围岩应力和变形解析公式. 侯公羽和牛晓松［16］基于levy-Mises本构关系及D-P屈服准则对轴对称圆巷进行了理想弹塑性的求解，弥补了Kastner公式中存在的缺陷. 潘阳等［17］基于H-B强度理论，采用极限平衡方程计算出隧道围岩的塑性半径、应力及位移公式. 张小波等［18］基于D-P强度理论，推导出隧道围岩的弹塑性区应力、塑性区半径和位移解析解. 董海龙和高全臣［19］基于M-C强度理论，用摄动法给出两向不等压作用下圆形巷道围岩弹塑性问题的二阶摄动解答. 上述研究成果有益地推进了隧道围岩弹塑性分析理论的发展.

值得注意的是，在针对中间主应力对隧道围岩应力及变形特征的影响方面还缺乏系统的研究. 因此，本文基于统一强度准则，推导了非均匀应力场下隧道围岩应力及塑性区半径解析解，以期为工程中隧道围岩应力及位移计算提供一定的理论基础.

1 统一强度准则

若规定压应力为正、拉应力为负［20］，则统一强度准则表达式为：

式中：σ1、σ2、σ3分别为最大主应力、中间主应力和最小主应力；c0为岩土的黏聚力；φ0为岩土的内摩擦角；b为中主应力系数［21］.

在平面应变条件下，统一强度准则满足下式：

式中：

式中：ct为统一黏聚力；φt为统一内摩擦角.

因此，在平面应变条件下基于统一强度准则的隧道围岩平衡方程为：

2 隧道围岩应力及塑性区半径计算

2.1 基本推导前提与假设

假设作用在隧道围岩的竖向应力为P0，水平应力为λP0，建立非均匀应力场下隧道围岩弹塑性计算简图，如图1所示. 其中r为围岩微元体的半径；θ为微元体与水平轴线的夹角，考虑到几何形状及受力形式的对称性，本文仅研究θ=［0°，90°］；R0为隧道半径；R为塑性区半径；λ为水平侧压力系数；σr为径向应力；σθ为切向应力；τrθ为剪切应力；Pi为支护反力.

2.2 非均匀应力场下隧道围岩弹性应力场

圆形隧道在非均匀应力场下可分解为均匀受压应力场和上下受压、左右受拉应力场的叠加，因此，图1中非均匀应力场下隧道围岩应力分析可转化为图2 中两种应力场的叠加.

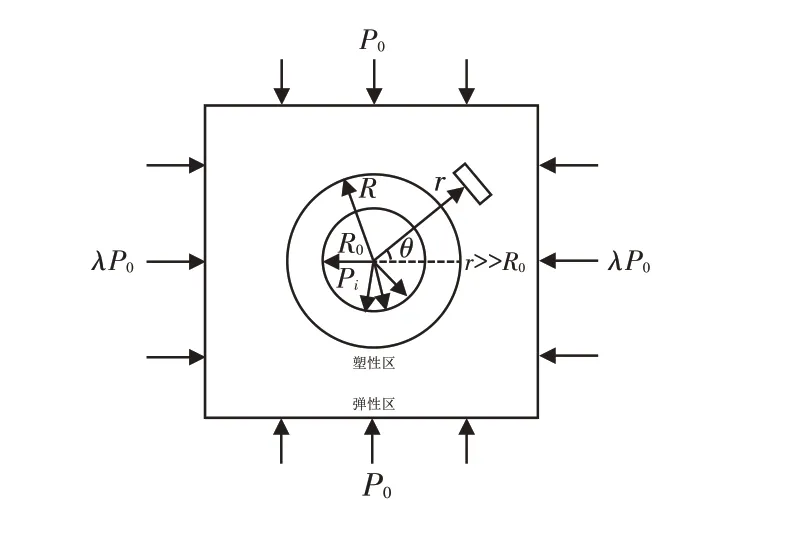
图1 非均匀应力场下隧道围岩应力计算简图Fig.1 Stress calculation diagram of tunnel surrounding rock under non-uniform stress field

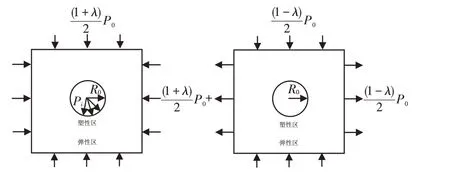
图2 非均匀应力场下隧道围岩弹性区应力分析Fig.2 Stress analysis of tunnel surrounding rock elastic zone under non-uniform stress field

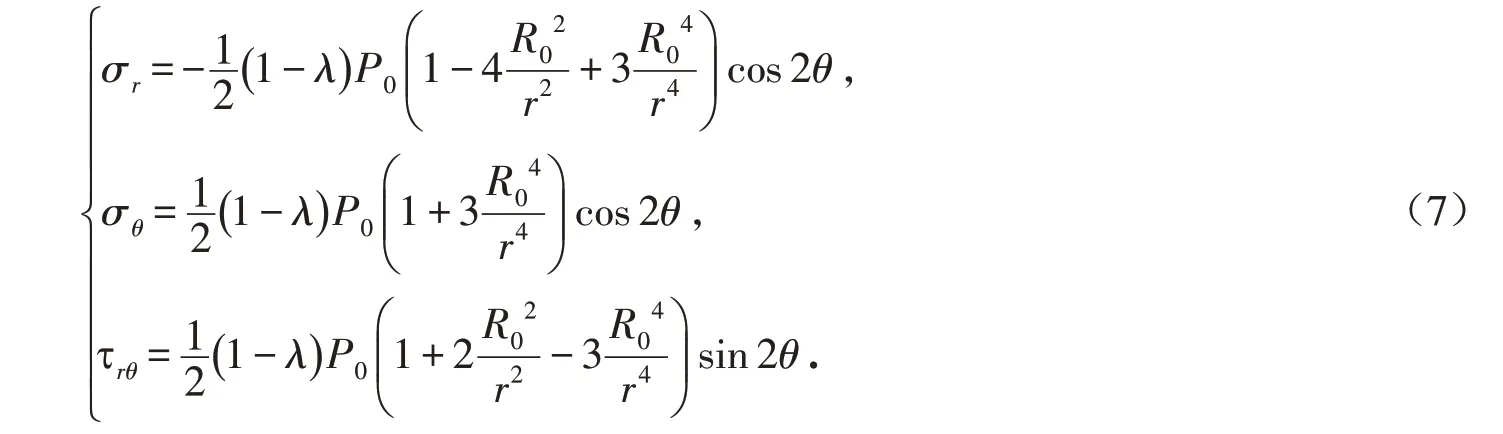
对上述两种应力场进行叠加，得非均匀应力场下隧道围岩应力表达式为：

2.3 非均匀应力场下隧道围岩弹塑性交界面应力

基于非均匀应力场的分解思路，得到轴对称圆形隧道在非均匀应力场下弹性区应力表达式为：

式中：σR为弹塑性交界面处径向应力.

当围岩微元体的半径r=R时，弹塑性交界面处围岩应力表达式为：

在平面应变条件下，隧道围岩满足统一强度准则的下半式（2），则主应力与隧道围岩应力关系为：

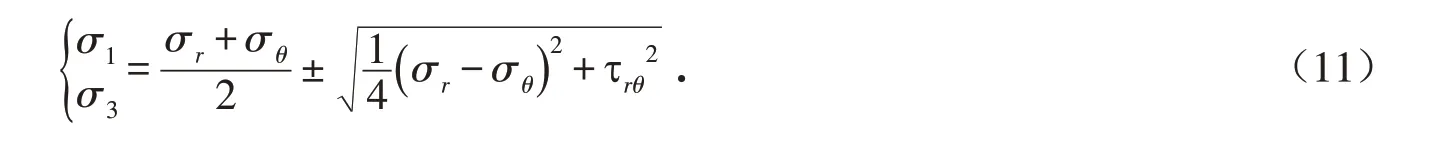
联立式（2）、式（10）和式（11），可得：

经计算得到非均匀应力场下隧道弹塑性交界面处径向应力表达式为：

将式（13）代入式（10），得到非均匀应力场下基于统一强度准则的隧道围岩弹塑性交界面上应力场解析表达式为：

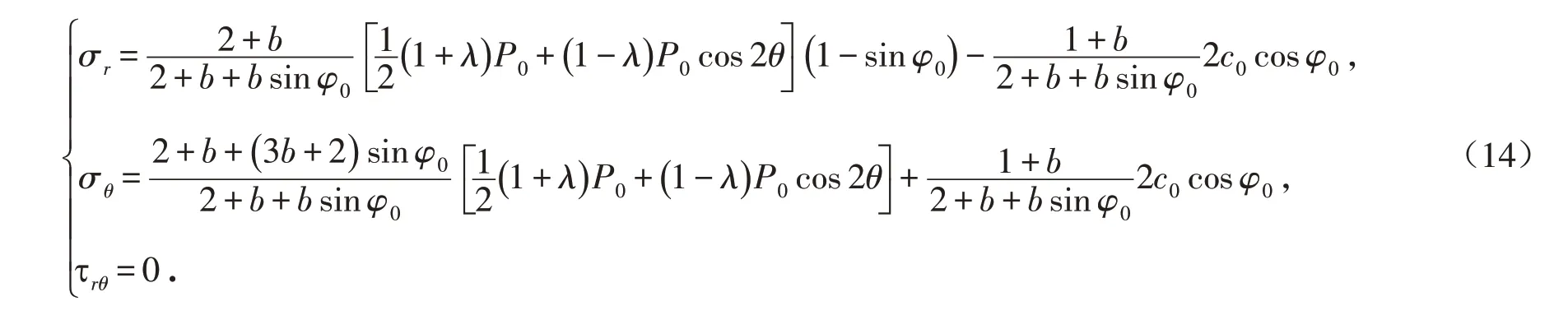
2.4 非均匀应力场下隧道围岩塑性区应力及半径

非均匀应力场条件下隧道围岩问题的平衡微分方程为：

隧道围岩问题的应力边界条件如下：

将式（11）代入式（5），可得下式：

联立式（15）、式（16）和式（17），得到非均匀应力场下基于统一强度准则的隧道围岩塑性区应力表达式为：

当隧道围岩微元体的半径r=R时，弹塑性交界面处围岩应力满足式（10），即存在如下关系：

基于隧道围岩弹塑性交界面处应力分量连续性的特点，联立式（18）、式（19），经计算得到非均匀应力场下基于统一强度准则的隧道围岩塑性区半径为：

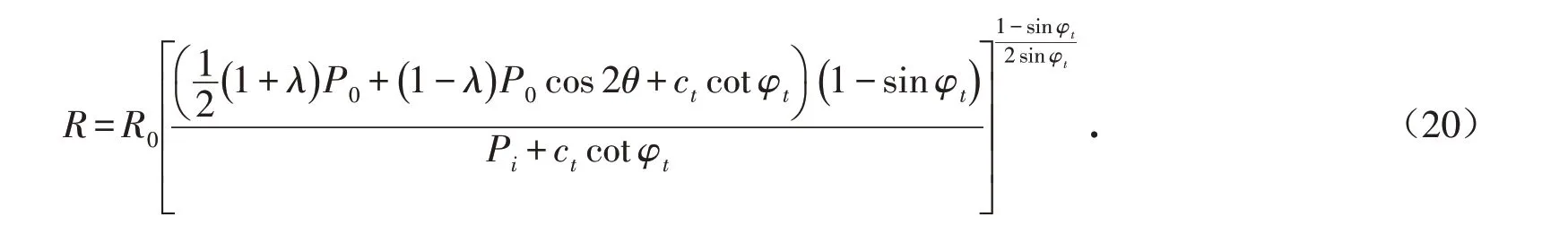
3 算例分析

本文选取圆形隧道半径R0=2 m，围岩重度为16 kN/m3，隧道埋深为50 m，则竖向应力P0=800 kPa，取水平侧压力系数λ为0.35和3.0，选取围岩力学参数如下：黏聚力c0=30 kPa，内摩擦角φ0=30°，支护反力Pi=0 kPa.

图3为水平侧压力系数λ=0.35 时非均匀应力场下基于统一强度准则的隧道围岩弹塑性交界面上应力分布曲线. 由图可知：隧道围岩弹塑性交界面上径向应力和切向应力均受中主应力系数b的影响，且呈现出b值越大，径向应力越小，切向应力越大的特点；在θ=0°时，不同b值条件下隧道围岩应力的差值最为明显，且随着θ值的增大，径向应力逐渐由压应力变为拉应力；以b=0时隧道围岩径向应力作为参照，随着b值的增大，径向应力依次减小5.8%、10.0%、13.2%和15.8%，以b=0 时切向应力作为参照，随着b值的增大，切向应力依次增大1.8%、3.1%、4.1%和4.9%；在θ=90°时（隧洞顶板），径向应力为负值，b=0、1.0时径向应力分别为-15.98 kPa和-21.12 kPa，两者径向应力相差32.2%.

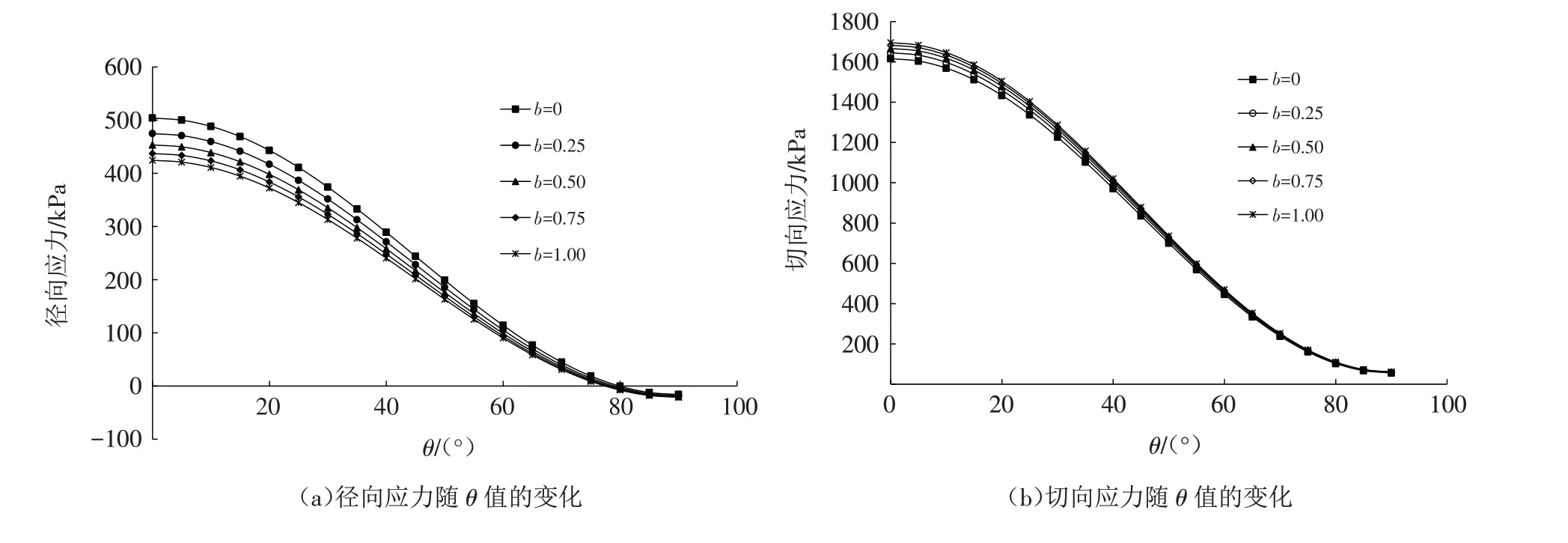
图3 λ=0.35时隧道围岩应力分布曲线Fig.3 The stress distribution curves of tunnel surrounding rock when λ=0.35

图4为λ=3.0时非均匀应力场下基于统一强度准则的隧道围岩弹塑性交界面上应力分布曲线. 由图可知：随着b值的增大，弹塑性交界面上径向应力减小，切向应力增大；在θ=0°时，隧道围岩应力的差值最小，且随着θ值的增大，径向应力逐渐由拉应力变为压应力；以b=0时隧道顶板围岩径向应力作为参照，随着b值的增大，径向应力依次减小5.4%、9.3%、12.4%和14.8%，以b=0时隧道顶板围岩切向应力作为参照，随着b值的增大，切向应力依次增大1.8%、3.1%、4.0%和4.8%；在θ=0°时，径向应力为负值，b=0、1.0时径向应力分别为-26.0 kPa和-29.7 kPa，两者径向应力相差14.2%.

图4 λ=3.0时隧道围岩应力分布曲线Fig.4 The stress distribution curves of tunnel surrounding rock when λ=3

综上，随着b值的增大，隧道围岩径向应力减小，切向应力增大；且当λ<1 时，围岩应力随着θ值的增大而减小，当λ>1 时，围岩应力随着θ值的增大而增大.

图5 为λ=0.35 时非均匀应力场下基于统一强度准则的隧道围岩塑性区半径分布曲线. 由图可知：隧道围岩塑性区半径随着b值的增大而减小；在θ=0°时，塑性区半径差异最为明显，θ值越大，塑性区半径越小，且θ=90°时（隧道顶板）塑性区半径最小；以θ=0°、b=0时塑性区半径作为参照，随着b值的增大，塑性区半径依次减小18.0%、27.9%、34.2%和38.5%；在θ=90°时（隧洞顶板），b=0、1.0 时塑性区半径分别为1.88 m 和1.76 m，两者相差6.4%.

图5 λ=0.35时塑性区半径分布曲线Fig.5 The plastic zone radius distribution curves when λ=0.35

图6为λ=3.0时非均匀应力场下基于统一强度准则的隧道围岩塑性区半径分布曲线. 由图可知：随着θ值的增大，塑性区半径逐渐增大，θ=90°时（隧道顶板）塑性区半径最大；以b=0 时隧道顶板围岩塑性区半径作为参照，随着b值的增大，塑性区半径依次减小22.4%、34.3%、41.5%和46.4%.

图6 λ=3.0时塑性区半径分布曲线Fig.6 The plastic zone radius distribution curves when λ=3.0

综上，随着中主应力系数b的增大，隧道围岩塑性区半径减小；且当λ<1 时，塑性区半径随着θ值的增大而减小，当λ>1 时，塑性区半径随着θ值的增大而增大. 表明非均匀应力场下基于Mohr-Coulomb强度准则的隧道围岩塑性区半径最大，在工程实践中大多数情况下是偏于保守的.

4 结论

1）本文基于统一强度准则，针对非均匀应力场下隧道围岩开展弹塑性分析，推导了隧道围岩应力及塑性区半径解析解，丰富了非均匀应力场下隧道围岩的弹塑性分析理论计算方法.

2）隧道弹塑性交界面上围岩应力和塑性区半径均受水平侧压力系数λ的影响. 当λ<1时，围岩应力和塑性区半径随着θ值的增大而减小；当λ>1时，两者随着θ值的增大而增大.

3）随着中主应力系数b值的增大，隧道围岩弹塑性交界面上径向应力减小，切向应力增大. 当λ<1时，在θ=0°时隧道围岩应力差值最为明显；当λ>1时，在隧道顶板处围岩应力的差值最大.

4）隧道围岩塑性区半径随着中主应力系数b值的增大而减小. 当λ<1时，塑性区半径随着θ值的增大而减小，隧道顶板处塑性区半径最小；当λ>1时，塑性区半径随着θ值的增大而增大，隧道顶板处塑性区半径最大.