基于CAE和CNN的变工况下滚动轴承智能故障诊断研究
周文宣, 刘 洋, 邓敏强, 丁 雪, 邓艾东
(1.国家能源集团宿迁发电有限公司,江苏宿迁 223803;2.东南大学 能源与环境学院, 火电机组振动国家工程研究中心,南京 210096)
滚动轴承是旋转机械设备中常用的零部件,其健康状态关系到设备运行的可靠性与稳定性[1]。但滚动轴承在高转速、重负载工况下长期运行,故障频发,若得不到及时维护,将导致设备其他零部件损坏,进而造成更大的经济损失。因此,实现对滚动轴承健康状态的准确识别具有重要意义。
受需求及环境等多种因素影响,滚动轴承并非在单一工况下运行,而是常常运行在变速变载荷条件下,工况变化在一定程度上增加了故障特征与故障模式间映射关系的复杂性,给机械设备的状态监测带来了巨大挑战。针对滚动轴承的故障诊断问题,国内外学者开展了大量的研究工作。以数字信号处理为基础的诊断方法研究较早,万书亭等[2]提出了一种融合概率主成分分析和Teager能量谱的特征提取方法;唐明等[3]提出了一种基于阶次解调谱的故障诊断方法。该类方法往往对专家经验有较强的依赖性,在变工况条件下应用有一定的局限性。随着机器学习技术的不断深入,基于数据驱动的轴承故障诊断方法取得较大的进展。张淑清等[4]提出用双树复小波分解振动信号进而提取故障特征,用深度信念网络实现轴承故障模式识别的方法;康守强等[5]提出了一种利用变分模态分解构造特征集与半监督迁移成分分析相结合的方法,在变工况条件下取得了良好效果。然而这些依赖于人工提取特征的方法难以实现设备故障的自动诊断。为了摆脱人工提取特征带来的限制,深度学习方法展现了巨大潜力,赵小强等[6]提出一种基于改进Alexnet的滚动轴承变工况故障诊断方法,将构建好的二维特征图输入到卷积神经网络中,实现了自适应特征提取,以进行轴承智能故障诊断。为了得到在变工况下故障诊断表现能力依然很强的特征,对于普通神经网络有必要选取足够多的训练样本,但在实际应用中往往难以满足。
笔者针对上述问题提出了一种基于卷积自编码(Convolutional Auto-encoders,CAE)和卷积神经网络(Convolutional Neural Networks, CNN)的轴承故障诊断模型CAECNN模型。该模型以单一工况下的数据作为源域,以变工况下的数据作为目标域。卷积自编码的编码器由多层卷积层组成,解码器由反卷积层组成,模型对源域和目标域数据进行训练,首先经过编码器获得特征参数矩阵F,然后输入到解码器得到重构数据并计算损失;轴承故障诊断模型为浅层卷积神经网络,其输入为源域数据经过编码器输出的特征参数矩阵F,输出轴承状态类别并计算损失;以上述两者的损失之和作为总损失进行训练,使源域与目标域数据经过编码器之后提取的特征分布更为接近,以此实现变工况下数据的特征域迁移,有助于CNN模型在变工况下的故障诊断。
1 算法原理
1.1 卷积神经网络
卷积神经网络经过多年的发展,已经在图像处理[7]等方面得到广泛应用。研究表明,通过卷积神经网络可以学习人工提取难以得到的深层次特征,因此有助于提高模型的判别能力和泛化能力。图1给出了常见的一维卷积神经网络结构。该卷积神经网络由输入层、卷积层、池化层、全连接层和输出层组成,卷积层和池化层两者交替设置。卷积层使用一定大小的卷积核对输入特征面的局部区域进行卷积运算,通过非线性激活函数后输出多个特征面,同一输入特征面与同一输出特征面中共用相同的卷积核,以实现权值共享,易于训练。池化层一般设置在卷积层之后,其输出的特征面一一对应于上一层卷积层输出的特征面,通过特定大小的窗口对局部接受域进行下采样,具有特征信息整合及降维的作用。
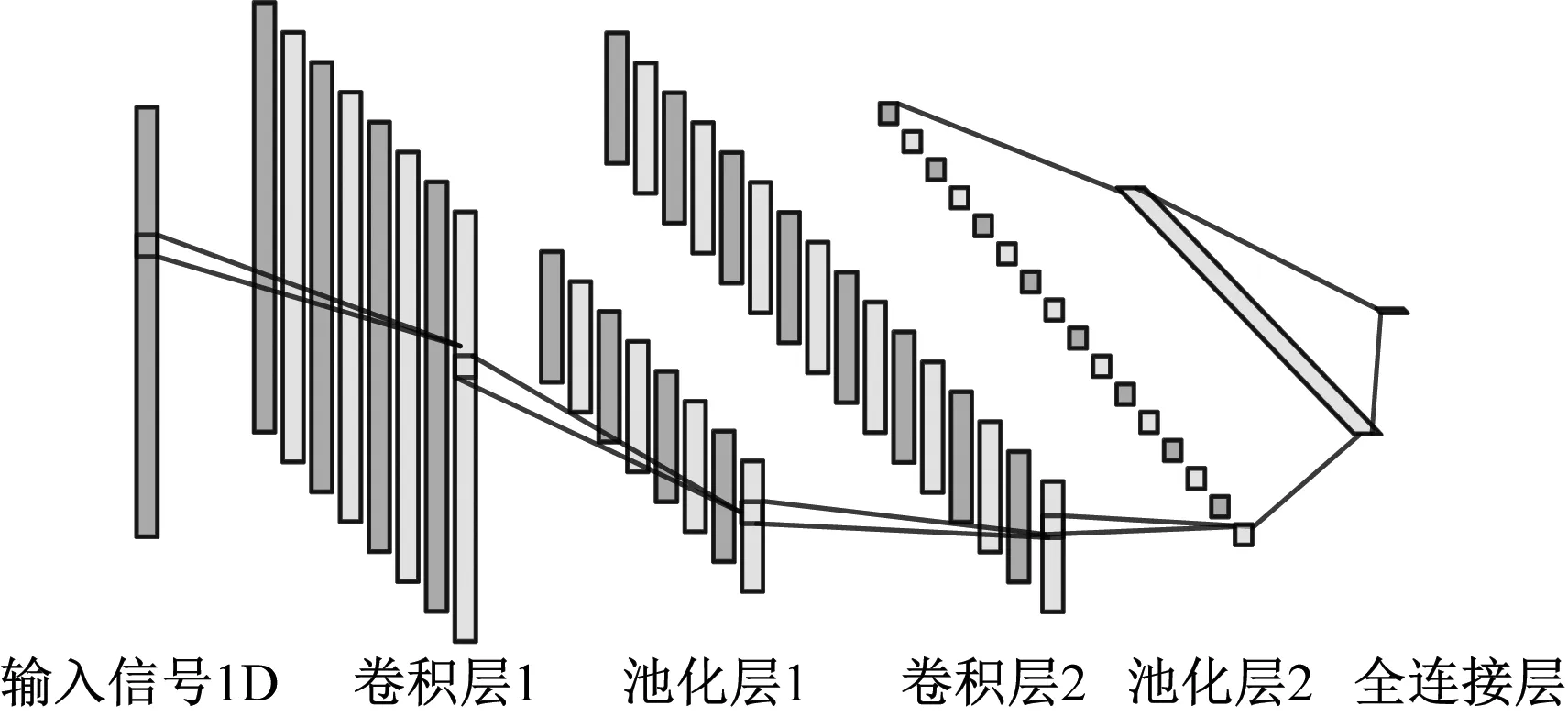
图1 一维卷积神经网络结构
反卷积又称为转置卷积,在场景分割、生成模型等领域得到广泛应用。卷积操作可以实现特征尺寸的减小,而反卷积操作可以使特征尺寸增大,其正向与反向传播运算为卷积操作的正向与反向传播的逆运算。
1.2 自编码神经网络
自编码神经网络(Auto-encoders Networks,AE)是一种基于数据重构思想的网络结构,其结构多样,常被应用于异常检测、模式识别[8]和噪声处理[9]等领域。图2为一个简单的自编码神经网络结构图,其结构主要由编码器和解码器组成,且两者结构对称,即神经元数量和层数相同,目标是通过学习使输出信号与输入信号之间的差别最小,传统的自编码神经网络的编码器和解码器都是由全连接层组成的,通常设置中间隐藏层神经元数量小于输入数据维度,可以起到特征提取、筛选和融合的作用。
自编码神经网络编码阶段和解码阶段的数学描述如下:
h=σe(W1x+b1)
(1)
y=σd(W2h+b2)
(2)
式中:h为隐藏层的输出值;σe和σd为激活函数;W1和b1分别为编码器的权重和偏置;W2和b2分别为解码器的权重和偏置;y为输出数据;x为输入数据。
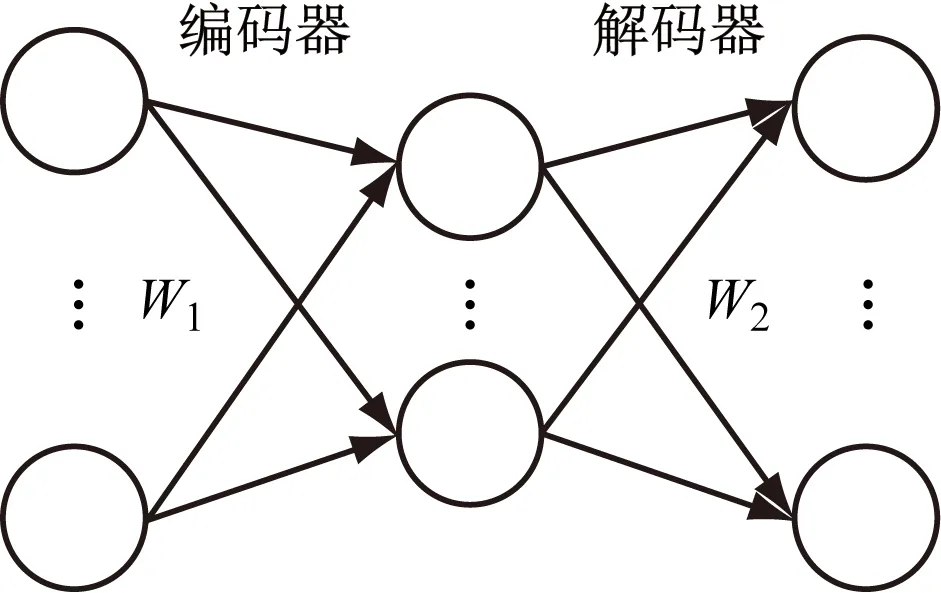
图2 自编码神经网络结构
1.3 卷积自编码神经网络
全连接神经网络结构较为单一,在提取深层次特征和多样性特征方面有一定的局限性,卷积神经网络的优异性能推动了卷积自编码的诞生,它是传统自编码神经网络的一个变种,图3为一个简单的卷积自编码神经网络结构图。卷积自编码的编码器和解码器不再使用全连接层,编码器被卷积层和池化层代替,解码器被反卷积层代替。卷积核数量和大小的多样化设置使卷积层相比全连接层具有更加强大的特征提取能力,尤其是在图像处理领域得到广泛的应用。
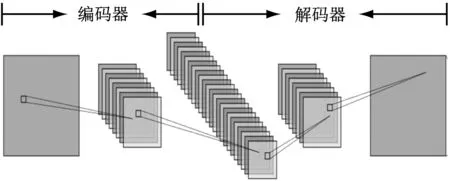
图3 卷积自编码神经网络结构
2 故障诊断方法
变工况下风电滚动轴承的故障特征不仅受到强背景噪声的干扰,也受到转速、扭矩等时变运行参数的影响。所提出的CAECNN模型将卷积自编码神经网络引入到基于卷积神经网络的轴承故障诊断模型中,其结构如图4所示,核心思想是以轴承故障诊断模型的中间特征空间作为迁移目标,利用卷积自编码实现变工况下数据特征域的自适应。卷积自编码的损失函数Lcae(x,y)为均方误差,如式(3)所示。轴承故障诊断模型采用交叉熵损失函数Lc(x,z),如式(4)所示。CAECNN模型的损失函数L(x,y,z)为两者之和,如式(5)所示。
(3)
(4)
L(x,y,z)=Lcae(x,y)+Lc(x,z)
(5)
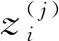
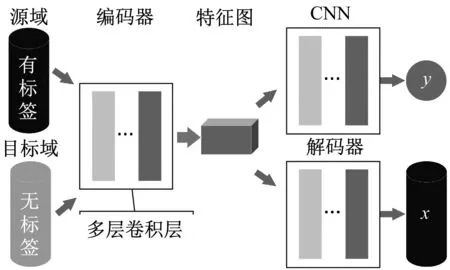
图4 CAECNN结构
CAECNN模型的网络参数如表1所示,其训练的基本流程如下:
(1) 获取数据。以某一工况下有标签的轴承振动信号数据为源域,变工况下的数据作为目标域。
(2) 将源域和目标域数据一起输入到编码器中得到特征参数矩阵F,然后输入到解码器中得到还原数据,并计算均方误差损失。
(3) 将源域数据的特征参数矩阵F输入到CNN中,输出轴承状态类别并计算交叉熵损失。
(4) 计算步骤(2)与步骤(3)的损失之和及其梯度,进行反向传播,更新模型参数。
(5) 重复步骤(2)~步骤(4),直到损失函数趋于稳定,模型训练结束。
(6) 将变工况下的数据先输入到编码器中得到特征参数矩阵F,然后输入到轴承故障诊断模型中得到状态类别,完成变工况下的轴承故障诊断。
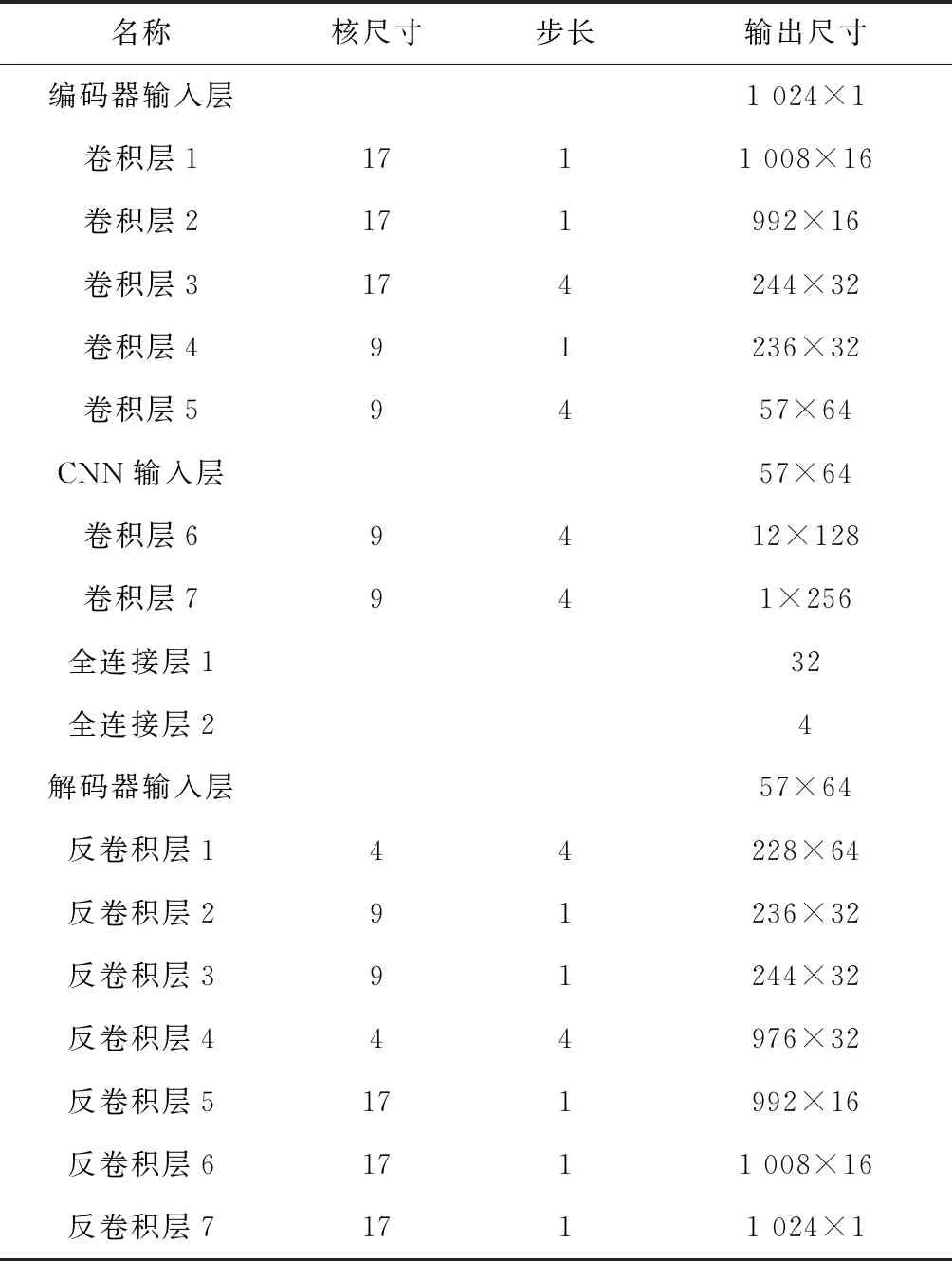
表1 CAECNN网络参数
3 实验验证
3.1 数据集介绍
考虑变负载和变转速都属于轴承变工况,本文的2个轴承数据集中数据集Ⅰ采用美国凯斯西储大学轴承数据中心的滚动轴承振动加速度数据,为变负载工况数据集;数据集Ⅱ选取加拿大渥太华大学的滚动轴承振动加速度数据,为变转速工况数据集。
数据集Ⅰ采集自电机驱动端的6205-2RS-JEM SKF型深沟球滚动轴承,信号采样频率为12 000 Hz,共有A、B、C、D 4种工况,具体见表2,每种工况包括4种状态类型:正常、内圈故障、外圈故障和滚动体故障。取1 024个数据点为一个样本,某一工况下每种状态类型有480个样本。
数据集Ⅱ测试轴承的型号为ER16K,主要包括正常、内圈故障和外圈故障3种类别的振动信号。在匀变速的工况下进行实验,转速的变化范围为900~1 620 r/min,信号的采样频率为200 000 Hz。取1 024个数据点为一个样本,某一工况下每种状态类型有120个样本,具体的实验样本情况见表3。
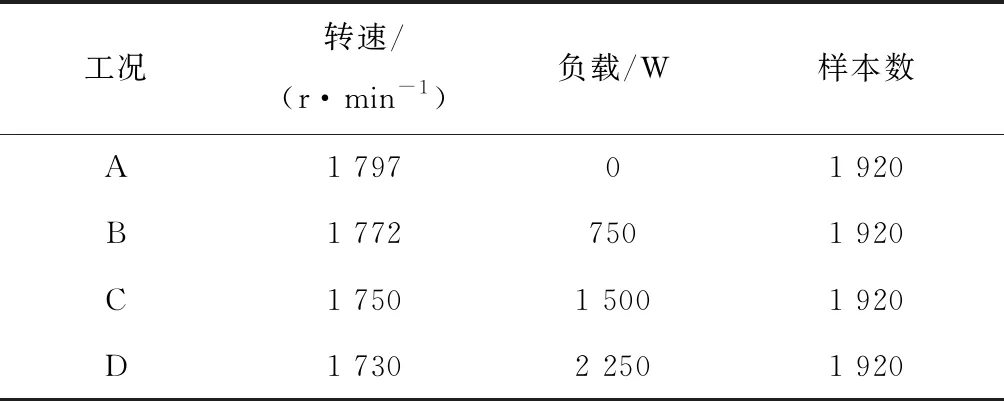
表2 数据集Ⅰ样本
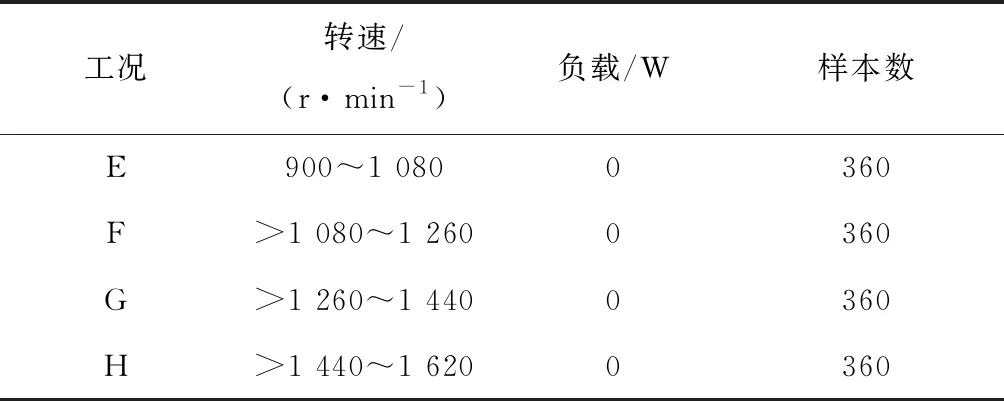
表3 数据集Ⅱ样本
3.2 对比模型设置
设置对比模型有以下3种:(1)CNN模型,即笔者所提模型中的CNN轴承故障诊断模型;(2)残差卷积神经网络ResCNN,其结构见参考文献[10];(3)支持向量机(SVM),提取的特征参数包括6个时域特征参数(均方根、峭度、偏度、波形因子、峰值因子和标准差)、5个频域特征参数(中心频率、均方频率、均方根频率、频率方差和频谱散度)和4个时频特征参数(包络阶次谱中旋转阶次以及滚动轴承内圈、外圈、滚动体故障特征阶次处的幅值)。
3.3 实验结果及分析
3.3.1 训练过程分析
本实验采用Pytorch深度学习框架,首先使用数据集Ⅰ进行验证,以0 W负载工况下的数据作为源域,并将数据划分为训练集、验证集和测试集,以其余工况下的数据作为目标域数据,全部数据作为测试集进行诊断效果评估。训练过程中采用Adam优化器,学习率为0.000 3,训练轮数为600,小批量mini-batch大小为32。图5给出了CAECNN模型训练过程中前100轮的损失函数。由图5可以看出,模型整体训练过程较好,在训练初期损失函数迅速下降,在30轮之后损失函数已经达到0.01,验证集诊断准确率达到100%,该过程中CNN模型和CAE模型的损失函数均迅速下降;之后损失函数开始平稳缓慢地下降,该过程主要是CAE模型损失函数的下降过程,600轮时损失函数为0.000 9,因其下降较缓慢不作展示。
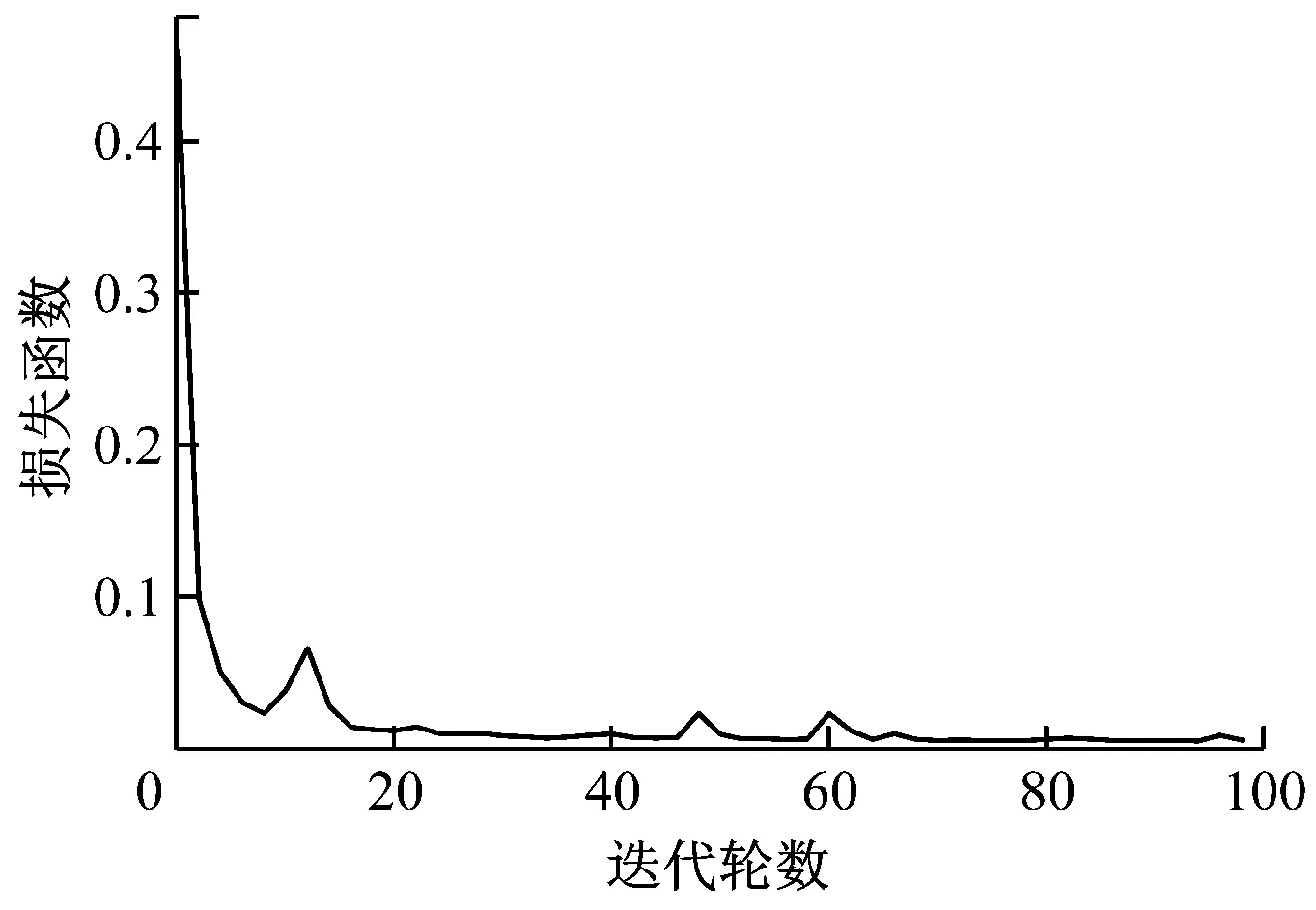
图5 损失函数
3.3.2 CAE模型训练结果分析
图6给出了数据集Ⅰ工况A下原始数据与经过CAE模型之后的重构数据的对比。由图6可以看出,原始数据与重构数据的波形图基本一致,由于CAE具有去噪功能,2种数据图仅存在一些细微的差别。此外经过600轮训练后,损失函数达到0.000 9,这也说明了CAE模型的训练效果较好。因此,经过编码器之后提取的特征参数矩阵F能很好地反映数据自身存在的一些性质。
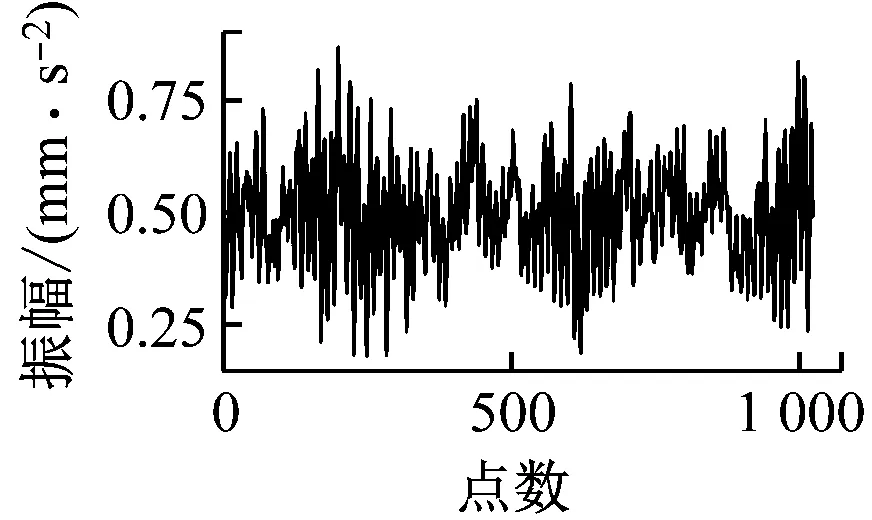
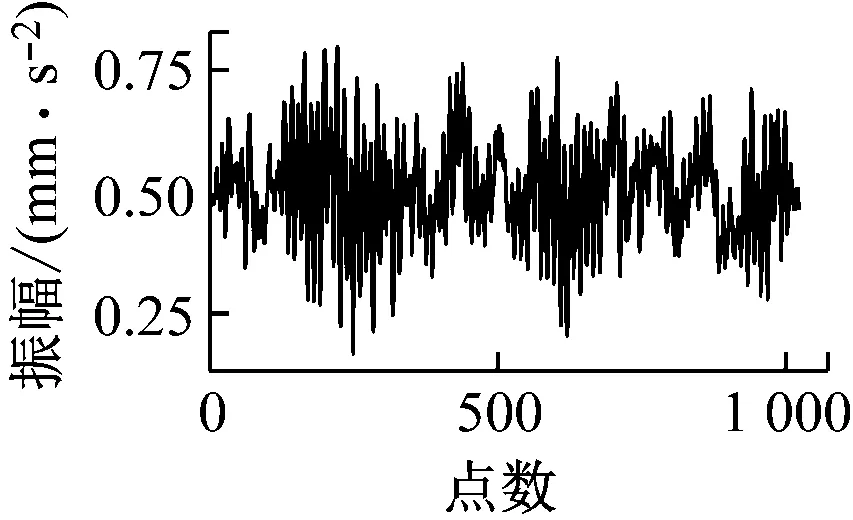
正常状态
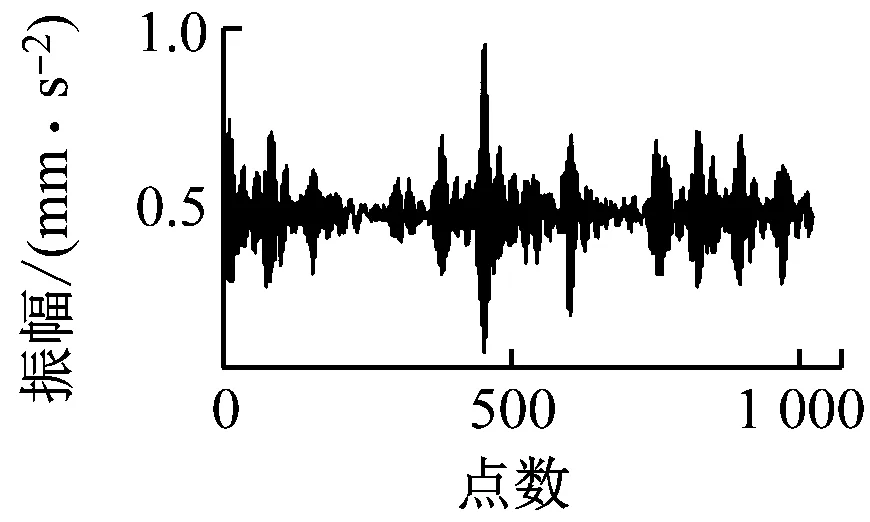
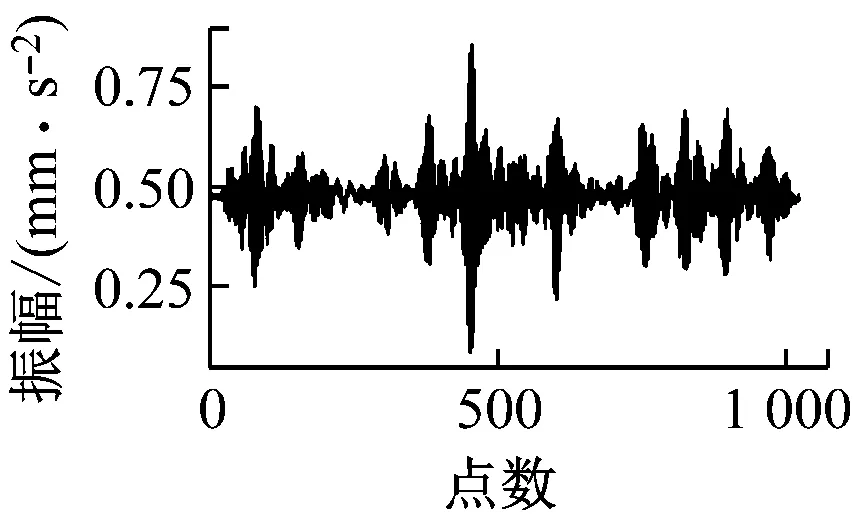
内圈故障
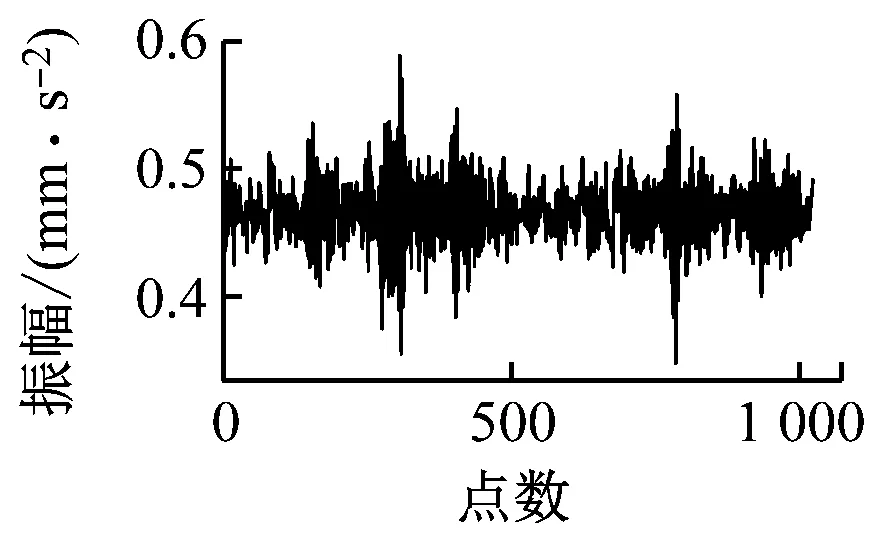
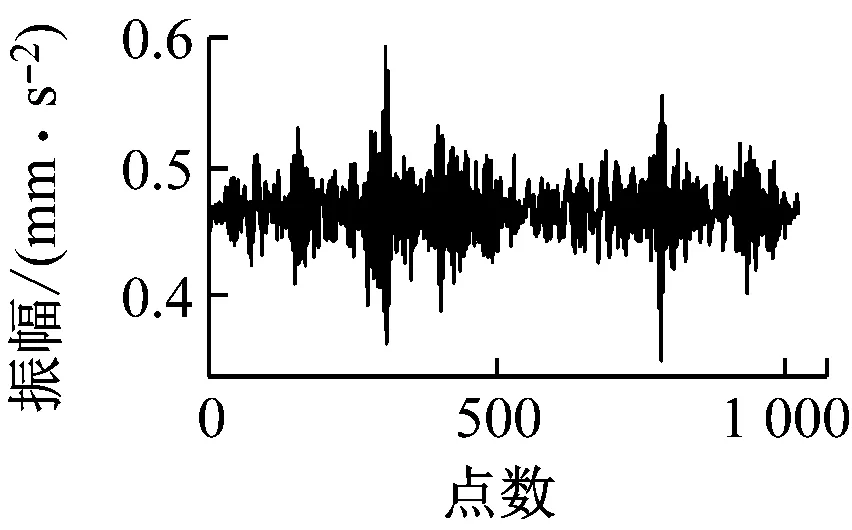
滚动体故障
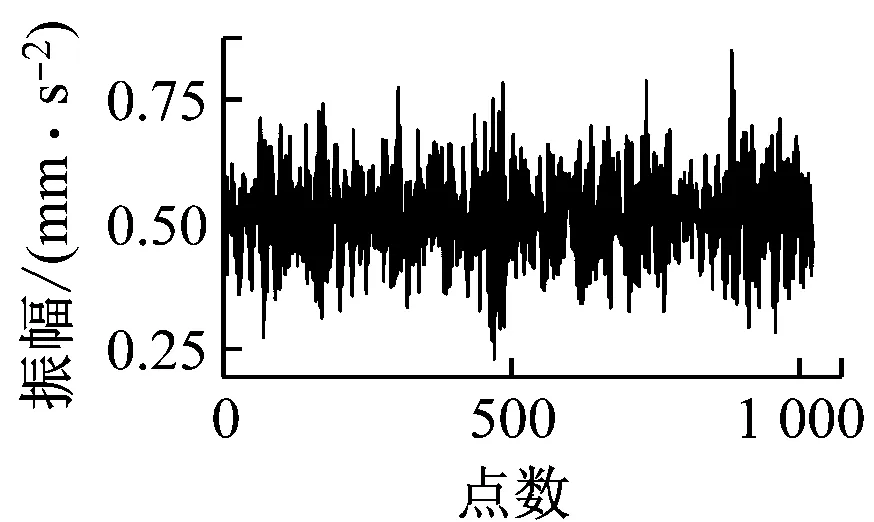
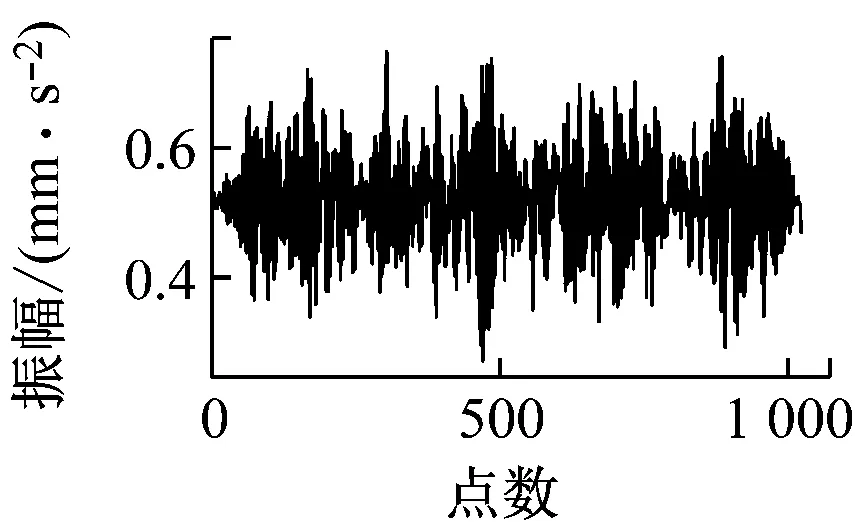
外圈故障
3.3.3 诊断准确率对比
为了对比所选取的4个模型的诊断效果,本实验以数据集Ⅰ工况A下的数据作为训练数据,并将其20%的数据作为测试集,为了模拟变工况条件,以其余负载工况下的全部数据作为测试集,各模型在测试集上的的诊断准确率如表4所示,每个模型中的每个诊断任务均是3次训练并预测取平均值的结果。由表4可以看出,对于A诊断任务,即工况A下的测试集,各模型的诊断准确率均较高,ResCNN、CNN、CAECNN模型的诊断准确率可以达到100%,SVM的诊断准确率达到97.6%,但是对于变工况下的数据,各模型的诊断准确率均有所下降。对比B、C、D诊断任务的诊断准确率以及平均值可以看出,基于人工提取特征的SVM在3个变工况下的故障诊断准确率均较低,其原因可能是所提取的特征并不具有很好的表达能力以及模型自身在变工况下的局限性;而ResCNN、CNN、CAECNN模型平均诊断准确率都高于92%,其中ResCNN在变工况下的诊断能力较为稳定且表现良好,在3个诊断任务上的诊断准确率均比CNN模型高。CAECNN模型的诊断准确率大幅提升,对于B、C诊断任务已经超过99.5%,对于D诊断任务的诊断准确率较低,为93.5%,但相比其他模型仍然具有优势,该模型的平均诊断准确率高于97%。
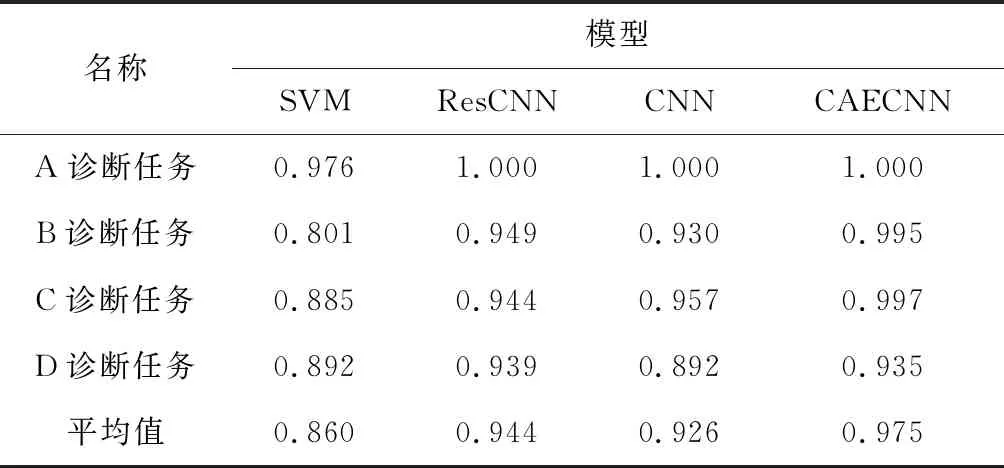
表4 测试集诊断准确率
3.3.4 变转速结果分析
为了验证CAECNN模型的普适性,使用数据集Ⅱ进行验证,以转速为900~1 080 r/min时的数据作为训练数据,其余转速下的数据视为变工况数据,各模型在各工况下的诊断准确率如图7所示,其中每个模型有E、F、G、H 4个诊断任务。由图7可以看出,在数据集Ⅱ上各个模型诊断准确率的分布规律与数据集Ⅰ上基本一致,基于人工提取特征的机器学习模型SVM的诊断效果最差,而CAECNN模型在CNN的基础上加入CAE,其诊断准确率有了较大的提升,证明了该模型的有效性。
4 结 论
(1) 所提出的CAECNN模型联合单一工况下有标签的数据和变工况下无标签的数据进行训练,变工况下其平均诊断准确率高于97%,相比未引入卷积自编码神经网络的CNN模型有了较大提升。

图7 诊断准确率
(2) CAECNN模型训练过程较为稳定,易于训练,且卷积自编码神经网络基于数据重构思想,有一定的降噪作用。CAECNN模型在变负载和变转速工况数据集上均表现良好,具有一定的普适性。

