站场旋转机械设备出口管道振动原因及减振方法研究

金佳旺，杨 平

中国石油天然气管道局国际事业部，河北 廊坊

1. 引言

站场是长输油气管线必不可少的设施，是管道运输的动力所在，如果将管线比作人的血管，那么站场便是人的心脏，为其正常运转提供能量，因此保障站场的安全运行至关重要。然而，站场管道振动问题经常伴随着管线的运行而存在，要知道振动是降低管道可靠性、引发管道事故的重要因素，据估计，全世界每年因管道振动而造成的经济损失高达数百亿美元[1] [2]，若能够妥善解决站场管道的振动问题，站场运行的安全问题将得到有效改善。

现已有不少学者和专家针对该类管道振动展开了研究。Enbin Liu 等[3]将管道的振动原因分为机械激励、流致振动、汽蚀振动三种，并针对不同压缩机管道振动的原因进行了总结；Trebuna Frantisek 等[4]-[9]提出压缩机管道在运行过程中，设备本身或流体介质都可能会对其产生影响，且通过测量、模拟分析，利用改善设备、管道支撑的方式可达到减振效果；Akintoye O. Oyelade 等[10]表示液或气两相同时在管道中流动时，就会产生两相流，这种情况会存在于石油和天然气工业应用中，准确预测这些管道的特性，以减少管道的振动疲劳失效是十分必要的；К. V. Boyarov 等[11]提供了一种新型阻尼减振结构，可在航空发动机、泵站管道系统中应用，以改善其大幅度振动；Hongfang Lu 等[12]从压力脉动出发，模拟了往复泵管道系统的振动响应情况，探究了压力、流量对振幅的影响；Gyun-Ho Gim 等[13]用有限元软件分析了流固耦合对管道固有频率的影响，结果表明水的存在会使管道固有频率降低；赵通来等[14]以弯头位置、曲率半径为变量探究了航空管道的模态变化规律。

由此可以看出，虽然在该方面已展开诸多研究，但仍存在些许不足。如在振动原因方面，当前只是针对泵站、压缩机站其中之一进行总结，没有对这两类站场所对应的振动原因进行统一的分类和共异性分析；在减振方面，多从管道侧入手，通过改善管道支撑的方式对振动进行了控制，其中部分学者对管道的模态规律进行了研究，但其考虑的影响因素相对较少、变量范围也相对较小。因此，本文对泵站、压缩机站旋转机械出口管道的振动原因、减振方法进行综合划分和解释，并在增加变量种类和范围的前提下，对模态规律进行了研究。

2. 振动机理

一个振动系统，通常具有三大要素，分别是质量、弹性以及阻尼。振动系统不同，三大要素的形式也会不同。对于单自由度系统，它通常包括一个定向振动的质量m、一个弹性元件刚度k以及运动过程中的阻尼c，其在激扰力 ( )

F t作用下的振动微分方程可按式(1)表示[15]：

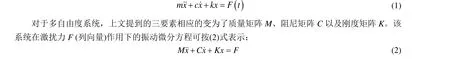
式中，x˙˙、x˙以及x分别为管道上点的加速度、速度以及位移的列向量，阶数与式中各项相对应。

激扰力的存在，便可能使得管道上点的x˙˙、x˙以及x发生改变，也就引发了管道的振动。

3. 管道振动原因

3.1. 机体自身振动

站场的旋转机械会由于自身设计、安装问题，如安装不牢固、转子偏移等，增添机体的不稳定性，导致机体在运行工程中产生位移，进而带动管道，换言之，就相当于在旋转机械出口管道处(管道的始端)强行施加了一个随时间变化的位移，这便引发或加剧了管道的振动。

3.2. 流致振动

无论是泵，还是压缩机，其动力供应都是周期性的，也就是所谓的压力脉动，这便会对管道产生激扰，尤其当压力脉动遇到阀门、弯头、三通等构件时，其激扰作用便会放大，在此激振力的作用下，管道便产生了振动。

当输送介质为液体时，对阀门、弯头、三通等构件的冲击更为明显，尤其当管道中存在多种介质时，如气、液两种介质，会由于两相所占比例、流速的不同，产生层流、波状流、段塞流等流型[16]，像段塞流这种极不稳定的流型，便会对管道产生极大的激扰。

3.3. 共振

在工程上，一般认为某阶固有频率等于激振频率的(0.8～1.2)倍时，即处于共振带范围内，便能够引发共振[17]。

3.3.1. 机械共振

对于机械振动而言，当管道固有频率和旋转机械激振频率之间存在上述倍数关系时，便引发共振。

1) 激振频率

对于压缩机管路系统，由振源发出的激振频率计算公式为[18]：

式中，n为压缩机的转速，r/min；i为谐波次数；m表示压缩机的叶片数或缸体数。

对于泵来说，其激振频率同样可按照上述公式计算，此时式(3)中的n为泵的转速r/min；i为谐波次数；m根据泵的种类不同可为泵的叶片数、缸体数、压力循环数。

2) 管道固有频率

固有频率为管道的固有属性，通过模态分析便可得出。模态分析时激振力为零，即使式(2)中的F向量为0，而阻尼通常忽略不计，因此振动体系的动力学方程可按式(4)表示：

对于无阻尼自由振动方程，其简谐形式的解为：

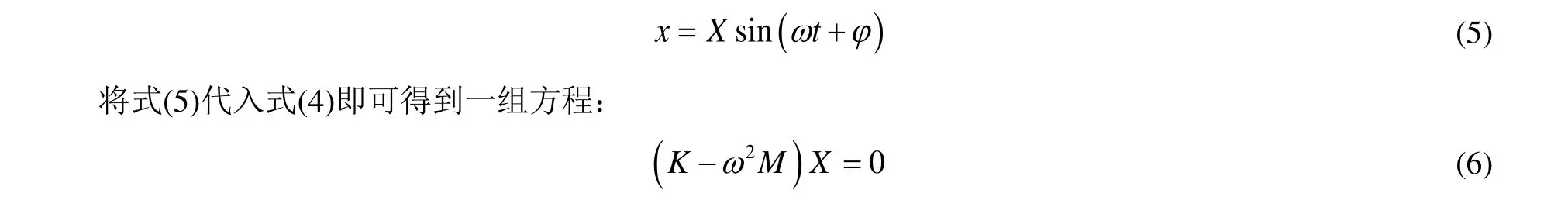
该小节公式中，X为非零的振幅向量，ω为圆频率，ϕ为相位角，其余同前文。

通过方程组(6)即可解得n个特征值和相应的特征向量，从特征值可以得知n个ω的大小，这些ω值即为该振动体系的各阶固有圆周频，通过f=ω2π 即可得到管道的固有频率。

3.3.2. 气柱共振

当气柱固有频率与激振频率存在上述倍数关系时，便引发共振。

1) 气柱固有频率

在压缩机气体管道中，气柱是一个有质量、连续性的可压缩振动体，因此管道内气柱具有一系列的振动频率，该频率即为气柱的固有频率。

2) 传递矩阵法

基于平面波理论的传递矩阵法是求解气柱固有频率的常用方法。对于管路来说，其存在多种元件，如直管、弯管、支线等，各元件首尾相连，每种元件均可求得一个转移矩阵，并最终构成了转移方程[19][20] [21] [22]：

3.3.3. 段塞流引发共振

如上所述，当管道中存在两相介质气和液时，在达到某种条件下，会形成段塞流，如图1 所示。该流型液体段塞和气泡交替流动，当该流型流经弯管等元件时会对管道产生周期性冲击，当该周期性对应的激振频率与管道固有频率之间存在上述倍数关系时，便引发共振。

Figure 1. Schematic diagram of slug flow图1. 段塞流示意图

由于段塞流不存在严格的周期性，各位学者、专家针对段塞流频率的计算方法各抒己见，因此目前还未形成统一且适用的计算方法，这里也便不再给出。

4. 振动控制方法

4.1. 主动控制

主动控制，即从振动的源头出发，减小激振力。可通过降低输送压力、输送量、增加输送的稳定性来达到目的，但由于工程效益问题，输送参数通常不能改变，因此大部分减振措施都采用被动控制。

4.2. 被动控制

被动控制，即从振体出发，通过提高振体的稳定性，来减振或抗振。现探究和总结了如下几种方法。

4.2.1. 改变管道结构

由以上振动原因可以发现，管道系统本身的固有频率对于管道的振动起着至关重要的作用。当管道固有频率偏低时，则振动容易被激起，甚至引发共振，因此可以通过改变管道固有频率的方式，来降低管道较大振动的可能性和避免管道各阶固有频率落于共振带而引发的共振。

本文以站场常见“U”型管道结构为基础，通过改变管道基础参数，如管径、曲率半径、壁厚等，探究了各参数对管道固有频率的影响，从而为站场管道的设计改造提供理论基础。

利用有限元软件，对管道进行建模。管道基本参数如表1 所示。在对网格进行划分时为保证网格质量，对弯曲处的网格进行了适当加密。管道的端点设为固定约束，即全约束。图2 即为所建管道模型及网格划分示意图。

Table 1. Basic pipeline parameters表1. 管道基本参数

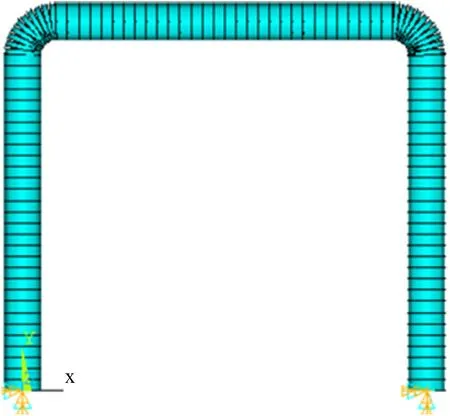
Figure 2. Schematic diagram of pipeline model and meshing图2. 管道模型及网格划分示意图

1) 管径的影响

管道的刚度和质量是影响管道固有频率的关键因素，改变管径的大小对于二者皆有影响，可以说管径是影响管道固有特性的一个间接因素，且通过管径来把控管道的固有频率也相对直接。从理论上来讲，管径对于管道刚度和质量的影响趋势是相同的，即管径增加，管道质量和刚度同时增加，反之，同时减小，无法直接判断管径对管道固有频率的影响规律。因此本文基于前文所建管道模型，在其他条件不变的前提下(此后默认其他条件不变)，分别计算了管径为273 mm、325 mm、377 mm、426 mm、478 mm、529 mm 时的管道各阶固有频率，其变化趋势如图3 所示。

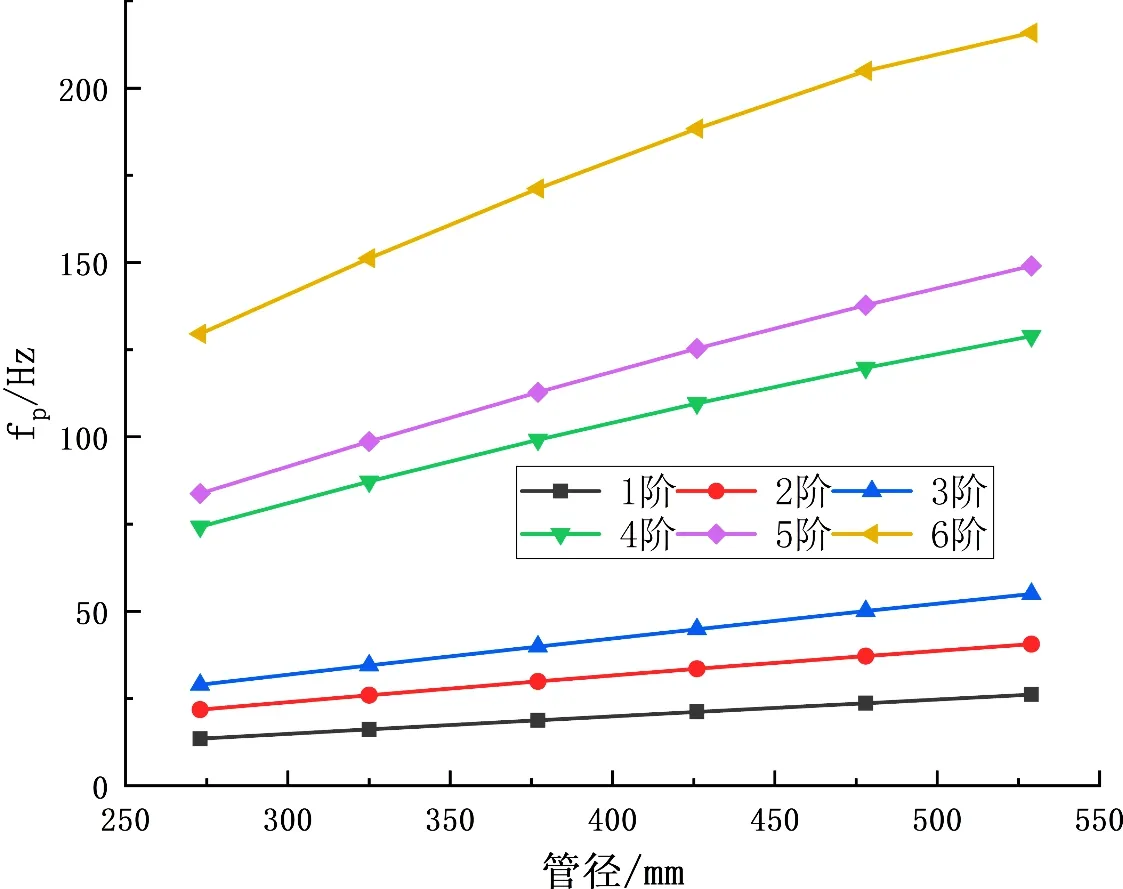
Figure 3. The influence of pipe diameter on natural frequency图3. 管径对固有频率的影响

由图3 可以看出，管道各阶固有频率随着管径的增大，都呈上升趋势(呈正相关)，且各阶固有频率的增长趋势随着阶数的增加逐渐增大。这说明了管径对管道刚度的影响强于对管道质量的影响，且对高阶固有频率的影响程度更深，两者差距更大。

2) 壁厚的影响

壁厚与管径类似，也间接影响着管道的刚度和质量且对二者的影响规律相同，因此本文对壁厚的影响规律展开了研究。计算了壁厚分别为9、11、13、15、17、19 mm 时的管道各阶固有频率，其变化趋势如图4 所示。

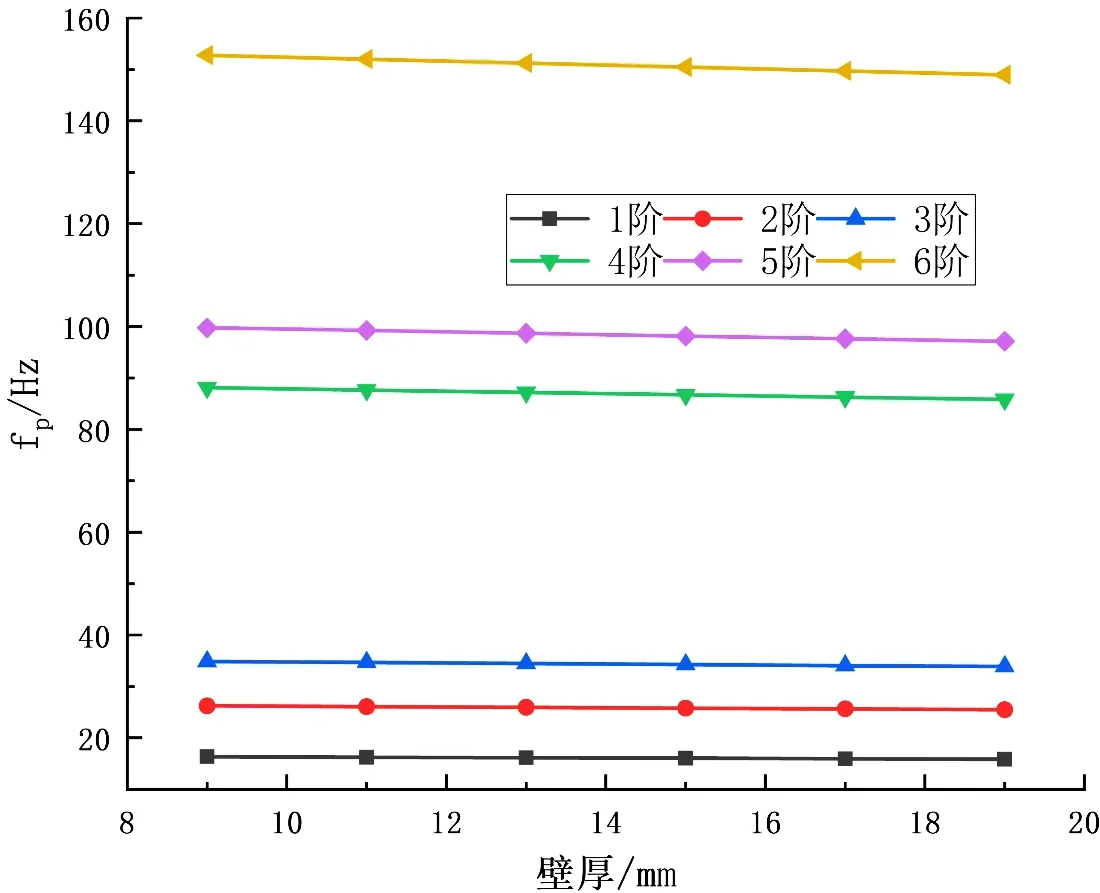
Figure 4. Influence of wall thickness on natural frequency图4. 壁厚对固有频率的影响

由图4 可以发现，管道各阶固有频率随着壁厚的增加呈下降趋势(呈负相关)，但相对平缓，由此可见，与管径的影响规律不同，壁厚对管道质量的影响程度要略大于对管道刚度的影响程度。

3) 曲率半径影响

用多大曲率的弯头会对管道的动态特性产生不同程度的影响，首先曲率的大小必然对管内介质的流动有所影响，再之，弯头的曲率属于管道的结构特征，不同的曲率会导致管道的固有属性存在些许差异，因此对其展开了研究。图5 即为固有频率随曲率半径的变化趋势图。

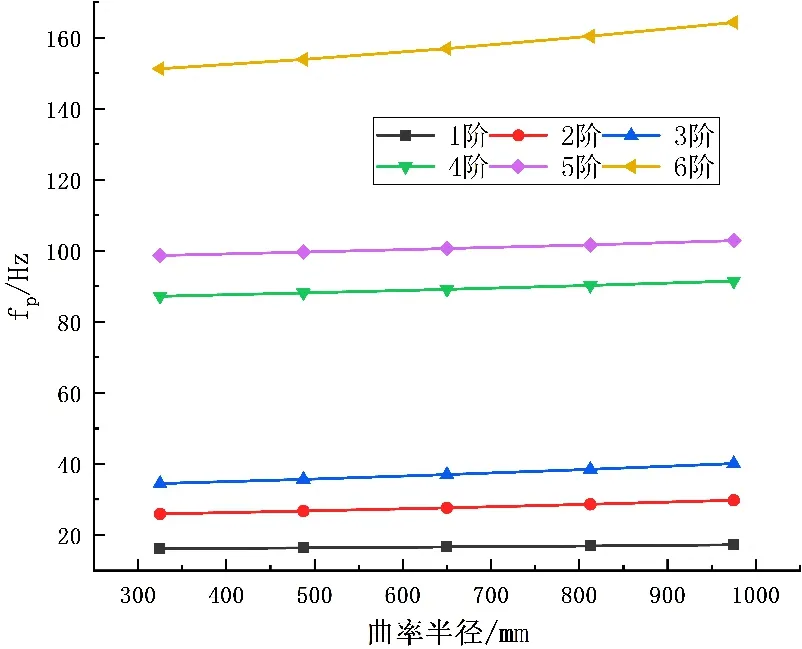
Figure 5. The influence of the radius of curvature on the natural frequency图5. 曲率半径对固有频率的影响

由图5 可以看出随着曲率半径的增大，各阶固有频率均为上升趋势(呈正相关)，且基频较为平缓。

4) 管内介质的影响

当管道的输送介质为液体时，管内介质与管道之间存在流固耦合作用，即管内介质流动会对管道产生作用，引发管道振动，管道振动又反过来影响介质的流动，这种流固耦合作用对管道固有频率的影响体现在管道系统质量的改变，因此本文通过附加质量的方式，探究了不同介质占比对管道固有频率的影响。首先分别计算出当管道内冷凝水占比为0%、10%、20%、30%、40%、50%时管道系统的整体密度，利用增加管道密度的方式，计算了各介质占比条件下的固有频率。各阶固有频率的变化趋势如图6 所示。

如图6 所示，各阶固有频率均随着介质占比的增加而降低(呈负相关)，且对高阶固有频率的影响较大。所以当输送介质为液体时，应考虑其对管道固有频率的影响，避免因管道固有频率的减小与激振频率达到共振。

5) 弯头位置的影响

管道的结构特征在某种程度上也影响着管道的振动特性，而弯头位置即弯头在哪弯恰好是管道结构的重要影响因素，因此本文以弯头位置为变量对管道的固有频率展开了研究。本文通过改变弯头与固定端的距离，但保持管道总长度不变(即相应的改变弯头之间的距离)的方式，计算了弯头与固定端的距离分别为0.5、1.0、1.5、2.0、2.5、3.0、3.5、4.0 m 时的管道固有频率。各阶固有频率的变化趋势如图7 所示。

如图7 所示，当弯头与固定端的距离小于1.5 m 时，基频随着此距离的增加而增大(这与参考文献[14]保持一致)，当大于1.5 m 时，基频随之减小；二阶固有频率的变化趋势与一阶基本一致。

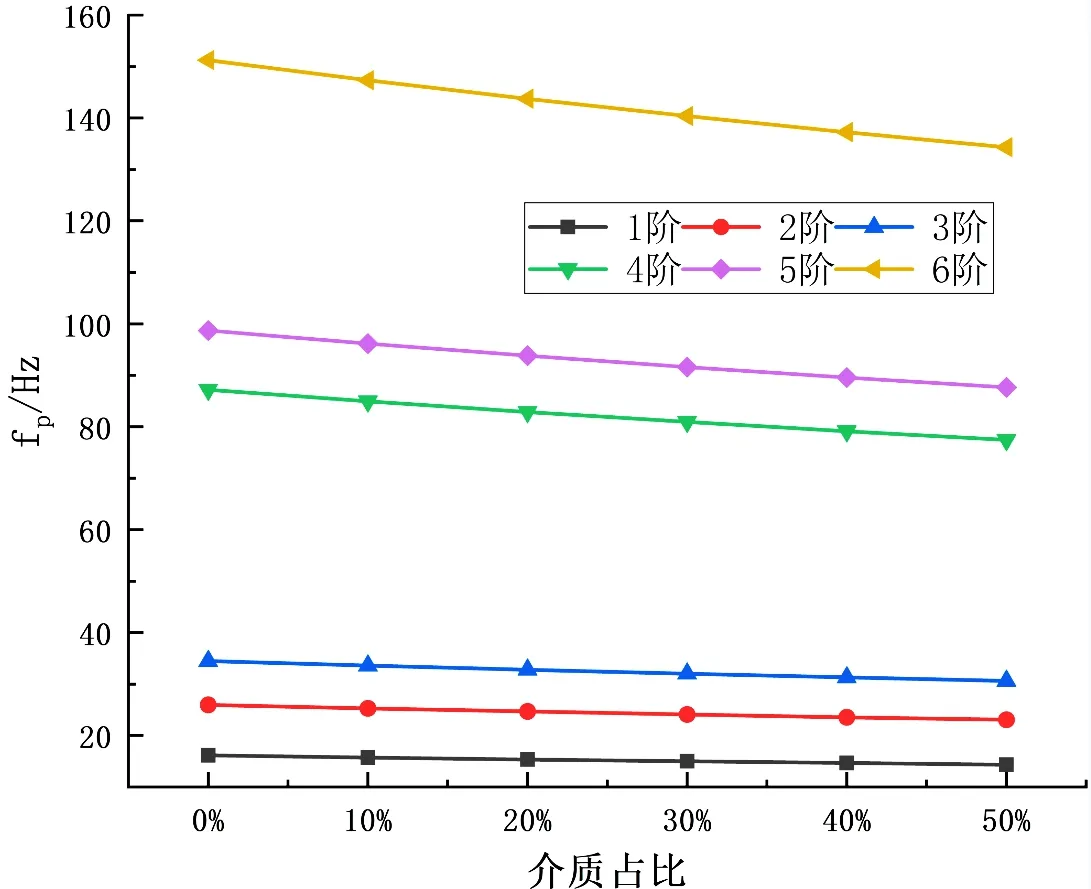
Figure 6. The influence of medium proportion on natural frequency图6. 介质占比对固有频率的影响

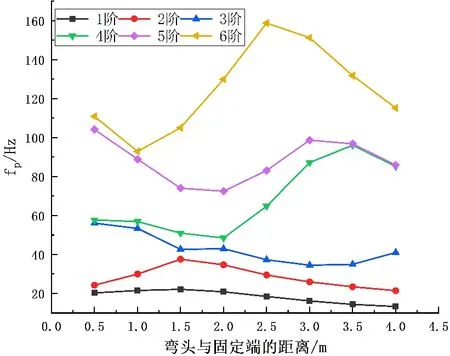
Figure 7. The influence of elbow position on natural frequency图7. 弯头位置对固有频率的影响

6) 管道长度的影响

管长同样可以影响到管道的振动特性，且与其它影响因素相比，管长的影响更为直接明显，如果管长过长，且约束施加不够，就极易引发管道的振动。这里同样是改变弯头与固定端的距离，不同的是，这里只改变这一距离，其它管道长度不随之而改变。分别将弯头与固定端的距离设置为1.5、2、2.5、3、3.5、4 m，即当直管总长分别为6、7、8、9、10、11 m 时，计算得出的各阶固有频率随管道长度的变化趋势如图8 所示。

由图8 可以看出管道各阶固有频率随管道长度的增加呈下降趋势，即呈负相关；对6 阶固有频率的影响最为显著。

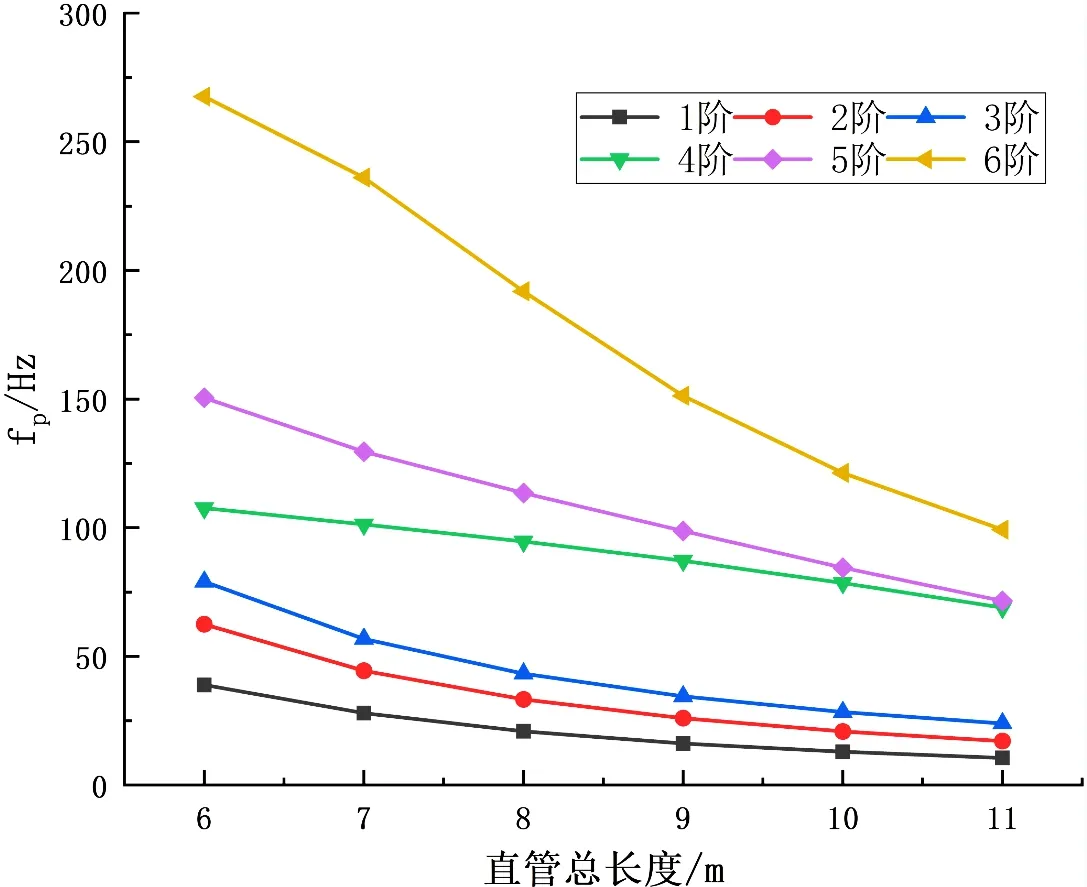
Figure 8. The influence of pipe length on natural frequency图8. 管道长度对固有频率的影响

4.2.2. 增加辅助设施

增加辅助设施是在役管道更为常用的减振方法，其一般可分为两种类型，如表2 所示。

Table 2. Auxiliary facilities表2. 辅助设施

5. 管道减振步骤

对于需要减振的在役管道来说，确定减振方案的过程基本相似，通常含有如下几个步骤：1) 确定激振力

查明激振力来源，是解决振动问题的第一步，唯有如此，才能进行更详细分析，进而找到解决方案。如前所述，常见的激振力来源有压力脉动、流体激振、旋转机械设备设计安装等。

2) 共振与否

共振能够引发管道大幅度振动，造成管道的位移或变形，甚至导致管道的失效。确认其是否发生共振，存在一定的优先级。

3) 振动响应

减振方案的确定通常需要仿真软件模拟真实的振动情况，以形成响应。

4) 提出减振措施

基于振动响应情况进行分析，拟定振动解决方案，并进行模拟，结合减振效果和经济性择优选择。

6. 结论

通过对站场旋转机械出口管道振动原因及减振措施的研究，得到主要结论如下：

1) 通过综合对比各类站场旋转机械设备管道系统的振动原因，将振动原因分为了如下三类：旋转机械自身振动、流致振动、共振，其中共振又可分为机械共振、气柱共振、段塞流共振。此外，还对各类振动原因做出了合理解释。

2) 将此类管道振动控制方法分为了主动、被动两种方式，其中被动控制方法更为常用。

3) 站场常见“U”型管道，其固有频率与管径、曲率半径呈正相关；与壁厚、介质占比、管长呈负相关；当弯头与固定端的距离小于1.5 m 时(弯头位置影响)，基频与此距离呈正相关，当大于1.5 m 时，呈负相关；二阶固有频率的变化趋势与一阶基本一致。可通过此类研究，为此类管道的设计提供理论基础，从而降低其发生振动的可能性。

4) 站场旋转机械设备管道系统振动控制方案的提出过程存在共性，其一般步骤如下：确定激振力、共振与否、振动响应，提出减振措施。