Barrier-Certified Learning-Enabled Safe Control Design for Systems Operating in Uncertain Environments

Zahra Marvi,,and Bahare Kiumarsi,

Abstract—This paper presents learning-enabled barriercertified safe controllers for systems that operate in a shared environment for which multiple systems with uncertain dynamics and behaviors interact.That is,safety constraints are imposed by not only the ego system’s own physical limitations but also other systems operating nearby.Since the model of the external agent is required to impose control barrier functions (CBFs) as safety constraints,a safety-aware loss function is defined and minimized to learn the uncertain and unknown behavior of external agents.More specifically,the loss function is defined based on barrier function error,instead of the system model error,and is minimized for both current samples as well as past samples stored in the memory to assure a fast and generalizable learning algorithm for approximating the safe set.The proposed model learning and CBF are then integrated together to form a learning-enabled zeroing CBF (L-ZCBF),which employs the approximated trajectory information of the external agents provided by the learned model but shrinks the safety boundary in case of an imminent safety violation using instantaneous sensory observations.It is shown that the proposed L-ZCBF assures the safety guarantees during learning and even in the face of inaccurate or simplified approximation of external agents,which is crucial in safety-critical applications in highly interactive environments.The efficacy of the proposed method is examined in a simulation of safe maneuver control of a vehicle in an urban area.

I.INTRODUCTION

TO deploy safety-critical systems in the real world,it is of vital importance to assure that their states evolve within a safe set under which satisfaction of their safety constraints is guaranteed.These safety constraints might be imposed either internally by physical limitations of the system (e.g.,actuator saturation) or by external environmental factors (e.g.,surrounding agents).Examples of environmental factors that affect the safety of a control system are a robot sharing its operational space with other robots in a factory and an autonomous car running in a shared road with other vehicles.Satisfaction of safety constraints is crucial and needs to be considered during the control design phase because their violation can have catastrophic consequences.Moreover,conflicts can always arise between safety and performance requirements,and,in a conflicting situation,safety objectives must always be prioritized to the performance.For example,in the adaptive cruise control system,the system’s performance level that can be achieved without safety violation in terms of reaching the desired speed depends on the traffic situation and assuring a safe maneuver (maintaining a safe distance from the vehicle ahead) must be prioritized to the performance.

Safe control methods based on control barrier functions(CBFs) have been successfully designed for a broad range of applications.This includes adaptive cruise control problem in[1],[2],safe control of robots [3],[4] and collision-free multiagents systems [5],[6].These methods generally integrate CBFs and control Lyapunov functions and solve a point-wise quadratic programming optimization problem to certify the safety and stability of a nominal controller.

CBFs are conceptually similar to Lyapunov functions and are used to ensure forward invariance of a specific set.However,these methods require complete knowledge of the system dynamics as well as the feasible set.Nevertheless,for the systems that operate in uncertain environments,the safe or feasible set is uncertain: safety criteria are affected by some external factors with possibly uncertain or unknown behaviors which are not known a priori.For example,in autonomous vehicles,the operation platform of vehicles is highly complicated and shared between autonomous,semi-autonomous,and human driving vehicles and pedestrians.Therefore,it is necessary to design a controller that can ensure the safety of the system despite the uncertainty in the feasible set due to the existence of unknown external agents while reaching as much performance as possible.

To account for uncertainties in designing safe controllers,several robust and adaptive approaches are presented.In [7],robustness of zeroing CBFs (ZCBFs) under model perturbation is investigated.It is shown that the existence of ZCBF ensures the input-to-state stability of the safe set under perturbations.However,external agents that affect the safety of the ego system cannot be modeled as perturbation.The fuzzy logic method is employed to model decentralized uncertain systems in [8].In [9],neural networks (NNs) are used to estimate the uncertain system,and a finite-time control design has ensured the boundedness of closed-loop signals.However,safety is not considered in [8] and [9].In [10],NNs are employed to approximate the system uncertainties,while integral barrier Lyapunov functions (BLFs) are employed to satisfy output constraints.In [11],time-varying integral BLF is employed to satisfy state constraints in a backstepping control design.In [12] and [13] NNs are used to adaptively compensate for the system uncertainty while barrier functions are used to satisfy state constraints.To deal with dynamic uncertainties in designing safe controllers,[4],[14] modeled uncertainties as a disturbance and learned it using a Gaussian process.The CBF is then formed and used to ensure safety for the worst-case disturbance.In [15],an adaptive CBF (aCBF)is proposed to ensure safety despite parametric uncertainty.To reduce conservatism,[16] proposed a robust aCBF (RaCBF),which guarantees forward invariance of a tightened set within the safe set.However,in both of these approaches,the invariance criterion needs to be satisfied for all possible values of the uncertain parameters that are not always known ahead of time.In addition,the effect of external dynamics in the environment shared with the ego-system can be completely modeled as neither parametric uncertainty nor disturbance.In [17],uncertainties impacting CBFs are learned to design a safe controller for a wider class of uncertainties.However,it is assumed that the CBF for the nominal system is a CBF for the uncertain system,which is not always applicable.

Safe reinforcement learning (RL) control design has also been recently considered in the literature for control of uncertain systems [3],[18].For instance,[3] proposed a safe RL framework for non-stationary dynamics using adaptive model learning and CBFs.However,although it is shown that the safe set is stable,strict safety might be violated because of non-stationarities.In [18],the utility function is augmented with CBF to plan for safety,and a safe off-policy algorithm is proposed.The approaches above are presented for singleagent systems.In [19],path planning in uncertain and dense obstacles environment is investigated in which a reachability set estimator of dynamic obstacles is employed to predict its threat.The CBF-based method,in contrast,ensures safety without the need for finding the reachability set,which is typically computationally demanding.Inverse RL is used in[20] to learn about the reward function and,consequently,the behavior of the human agent in control of human-robot systems.However,this line of work assumes that the human operators or external agents choose their course of actions based on a perfectly rational framework that makes optimal decisions with respect to a reward function,which might not coincide with reality and is also computationally expensive.

This paper presents a method for designing a learning-enabled safe controller for systems that must operate in environments that are shared with other agents with uncertain behaviors: The behaviors of surrounding agents affect the safe set and thus safe control design of the ego system,which are unknown and uncontrollable from the ego system’s perspective.This is in sharp contrast with existing safe control methods requiring complete knowledge of the safe set.The uncertainty of the safe set caused by the uncertain behaviors of surrounding agents makes safe control design much more challenging.Fast and sample-efficient learning of uncertainties is of vital importance to avoid an overly conservative control design (which can also result in infeasibility) or unsafe behavior.A slow model-learning approach also avoids proactive safe control design,which can jeopardize the performance.Moreover,and even more importantly,a naive model learning approach based on minimizing the modeling error cannot account for safety even if the expected estimation error decreases over time; This is because different models with the same modeling errors might have different characteristics in preserving the invariant behaviors of the actual system: Novel learning algorithms are required to avoid misrepresentation of the safe set as much as possible.

The interaction between agents is formulated using two sets of decoupled differential equations corresponding to the ego system and the risk-imposing external agent.A safety criterion is defined as a function of both subsystems’ states.This is in sharp contrast with the existing works,which only consider partial uncertainty in the system dynamics and define the safety criterion solely based on the ego-system’s states.The proposed framework is far more inclusive for safetycritical control scenarios where the agent operates in a cluttered uncertain environment shared with other agents.Since the trajectory information is required to form ZCBFs,the unknown external agent dynamics needs to be learned.To make less conservative decisions and avoid misrepresentation of the safe set,a safety-aware model-learning approach that leverages safety-aware loss functions and the experience replay method is presented to learn uncertain and unknown behavior of the external agent.More specifically,the loss function is defined based on the barrier function error,instead of the system model error,and is minimized for both current samples and past samples stored in the memory to assure a fast and generalizable learning algorithm for approximating the safe set.Moreover,it provides an easy-to-verify metric on collected data to assure learning of the actual safe set,allowing to make more informative control decisions.Then,a learning-enabled ZCBF (L-ZCBF) is presented that integrates the proposed safety-aware model learning and a novel ZCBF to assure the safety of the ego system in the presence of uncertainty in the behavior of its surrounding agents.Since ensuring forward invariance of the approximated safe set does not necessarily ensure forward invariance of the actual safe set and strict safety might be violated,L-ZCBF employs the approximated trajectory of external agent and also the trajectory of ego-system,but shrinks the boundary of the safe set in case of an imminent risk that can be predicted using observations of the states of the external agents.These observations can be acquired using embedded sensors such as light detection and ranging (LIDAR).Guaranteeing forward invariance of the intersection of the approximated safe set and the actual safe set assures safety during learning and automatically shrinks the boundary of the safe set to the extent that safety of the overall system is guaranteed despite uncertainty.As learning enhances,this set expands to the actual safe set.

In a nutshell,the contributions of the paper are as follows.

1) The problem of safe control design for systems operating in uncertain shared environments is formulated as two sets of decoupled dynamics with a safety criterion defined as a function of both ego and external agent’s states to have a more inclusive scheme for safety-critical systems operating in the cluttered environment.

2) A novel learning-enabled ZCBF is proposed,which is capable of safety guarantee during learning of unknown dynamics.

3) The safety-aware model learning is proposed for rapid convergence of the approximated safe set to the exact one.

A.Organization of the Paper

Section II provides the problem statement as well as preliminaries and background information.The main idea of learning-enabled ZCBFs for uncertain sets is presented in Section III.Section IV represents the overall control framework and the proposed algorithm.Case study,simulation results,and conclusion are given in Sections V–VII,respectively.

B.Notation

Script notation is used for denoting sets such as C .intC indicates the interior of the set C and ∂C stands for its boundary.X ⊂Rnis the state space and U ⊂Rmis the set of all admissible control inputs.C1denotes the set of all continuously differentiable functions.‖x‖ indicates the Euclidean norm ofx.

II.PROBLEM STATEMENT AND BACKGROUND

In this section,the safe control problem in the presence of external agents is stated,and some background information on ZCBFs and safe control design is provided.

A.Problem Statement

Consider the control system in the nonlinear affine form as

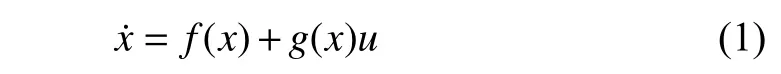
wherex∈X andu∈U are the states of the controlled system and the control input,respectively.f(x)∈Rnis its drift dynamics andg(x)∈Rn×mis its input dynamics.f(x) isC1andf(0)=0.It is assumed that the ego system is stab ilizable and Uis non-empty.

The goal is to ensure the safety of the control system (1) in a shared environment with external agents with uncertain and unknown behaviors.The dynamics of the external agents that affect the safety of (1) is given as

which is unknown and out of control of the ego system andz=[z1,...,zp2]is the state vector of external agents which can be measured in real-time by the ego system(e.g.,measuring the position of a leading vehicle using embedded sensors that measure the distance and relative steering) andf2∈Rp2is assumed to be locally Lipschitz.Note that (2) does not need to capture the complete dynamical behavior of external agents in the surrounding environment,as it might require high-dimensional dynamics,which makes their learning computationally intractable; rather,it concerns simplified dynamics that best captures the effect of external agents on the safety of the ego system.For example,in urban driving,distance to other agents and obstacles and how they are approaching the ego vehicle matter most when safety is the main concern.The safety of the ego system is then formulated as a function of bothxandz,which is uncertain due to unknown dynamics ofz.

It is desired to satisfy uncertain safety criteria which are impacted by states of the system (1) and the external dynamics(2) and achieve stability and performance specifications as long as it is safe.

Control Objectives:The following objectives must be achieved for the system (1).

1) Assuring safety by guaranteeing that the following safety conditions are satisfied all the time:

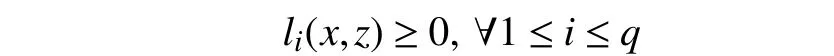
whereli(x,z)＞0 is theith element of the safety criteria which is a smooth function describing a constraint on the system,andqis the total number of constraints.

2) Guaranteeing stability of the controlled system,i.e.,x→0 ast→∞ in the case of no conflict with safety.

The safe set is formed as the intersection of all the sets,each satisfying a safety constraint.That is,the safe set is defined as

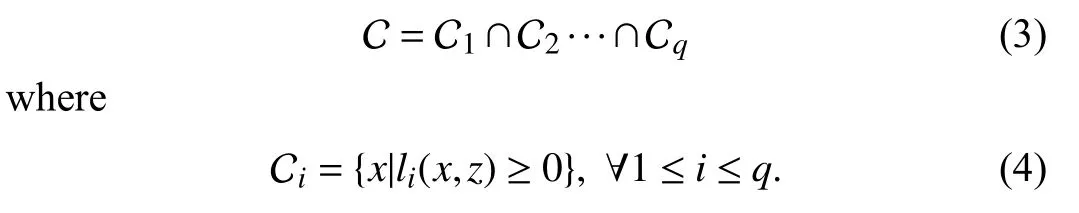
Safety imposes hard constraints on the control design,while performance is a soft constraint satisfied in the case of no conflict with safety.

Remark1:Note that two sets of dynamics are considered in this framework in which (1) represents the first one and is known,and (2) represents the second one and is assumed to be uncertain and unknown.The safety set is represented as a function of both dynamics’ states (4).Therefore,even when the dynamics of the ego system is partially available,this method is applicable since this unknown part is included in (2)which is learned.Therefore,this covers not only disturbances that can be learned by collecting data but also a more general class of uncertainties in the environment and the ego-system dynamics.

B.Control Barrier Functions

Guaranteeing positive invariance of a set of states has broad applications in control system design,such as control of constrained systems and region of attraction maximization.For a dynamical system,positive invariance of a set means that inclusion of states in a specific set at any time ensures the inclusion of states in that set in the future time.Extension of this notion to control systems is called controlled positive invariance of a set,which guarantees forward invariance of the set by designing a proper control input.One of the widely referred theorems in the characterization of positive invariant sets is the Nagumo’s theorem [21]–[23].This theorem is presented using the concept of the tangent cone of a set [23],[24].

Theorem 1: Nagumo’s Theorem

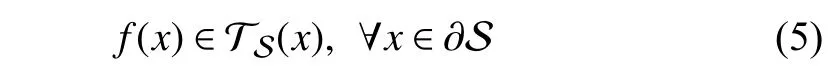
where ∂ S is the boundary of the set S and TS(x) is the tangent coneto S.

Proof:See Theorem 3.1 in [22] and Theorem 4.7 in [23].

Remark 2:The Nagumo’s theorem implies that to have a positive (forward) invariant set,x˙ should point inside the set at the boundary,or in the worst case,it should be tangent to the boundary.

CBFs are used to ensure forward invariance of a specific set in a control system.ZCBF is a positive function within a set and zero at its boundary and thus,having a zeroing derivative in the vicinity of the boundary prevents the states of the system from exceeding the limits.Theretofore,forward invariance of the set is ensured while handling unbounded functions are avoided [2].Based on the definition of classK function in [25],extended class K function is defined as follows.

Definition 1:A continuous functionα:(-b,a)→(-∞,∞)witha,b＞0 is an extended class K function,if it is strictly increasing and α (0)=0 (Definition 1 in [7]).

Definition 2: ZCBF Properties

For the control system (1) and a given setM ⊆D ⊂Rndefined as

theC1functionl:Rn→R is a ZCBF on the set D,if there exists an extended class K functionαsuch that

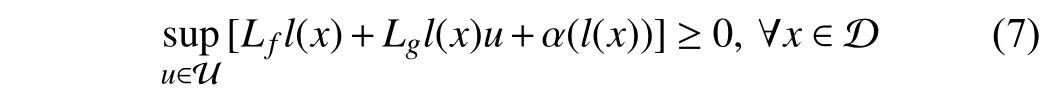
whereLfandLgare Lie derivatives ofl(x) alongfandg,respectively,and

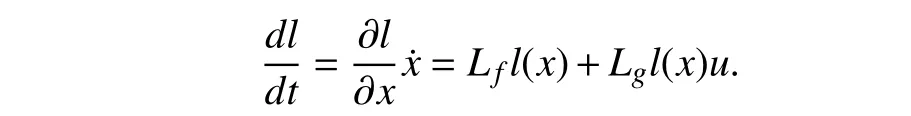
Then,the set of inputs that satisfy (7) is

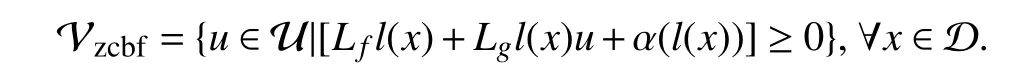
Lemma 1:For the given set M ⊆D ⊂Rnwith functionl; iflis a ZCBF on D,then,any Lipschitz continuous controlleru∈Vzcbffor the system (1) renders the set M forward invariant.

Proof:See Proposition 1 in [2].

In safety-critical control systems,the safe set is presented by M with a safety criterion expressed byl(x)≥0 as (6).By starting from a safe initial conditionx0∈M and selection of a control input that satisfies (7),the system never leaves M and thus guaranteeing safety.Despite the incredible power of ZCBFs in ensuring the safety of control systems,this method faces a couple of challenges.First of all,to ensure the satisfaction of (7),complete information about the dynamics of the system is needed.Second,the safety criteria and the safe set are assumed to be certain and known.However,in many real scenarios,the safe set is uncertain and affected by unknown external dynamics as described in (4).In the following section,the application of ZCBFs to guarantee safety under uncertain safety criteria in the presence of unknown external dynamics is investigated.

III.LEARNING-ENABLED ZCBF WITH UNCERTAIN SETS

The system is considered to be operating in an environment that is shared with other agents.These external agents impose safety consideration on the system,while their dynamics are unknown and uncontrollable.This results in uncertainty in the environment and designing a safe controller.Therefore,in this section,the L-ZCBF platform is presented to ensure safety despite uncertainty in the behavior of external agents.The influential unknown dynamics of the external agents are learned,and consequently,an L-ZCBF is formed that assures the forward invariance of a set that is contained in the safe set,and its size becomes closer to the size of the actual safe set as the learning progresses.

A.Learning Safe Set Despite Uncertain Behaviors of External Agents

In order to design a safe controller for (1) in the presence of uncertain external agents in the environment,first,influential dynamics of external agents need to be approximated.Considering the Lipschitz continuity assumption onf2and the fact that any smooth function within a compact set can be approximated by an NN [26],(2) is approximated as

whereis the estimated NN weights and Φ is its activation function.Then,considering (4),the approximated safe set is defined as

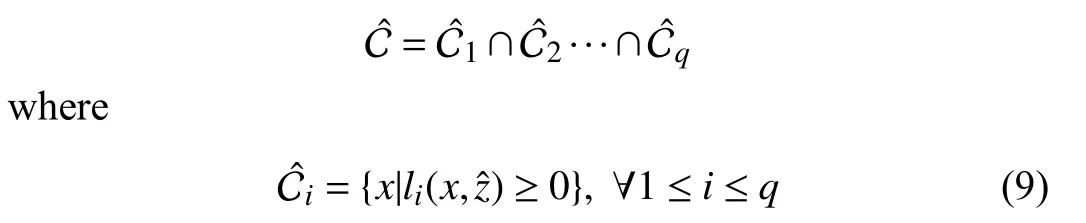
whereis the state of the approximated external dynamics represented in (8).Fig.1 shows an example with both the actual safe set and its approximated one for a specific time.As can be seen from Fig.1(a),designing a controller based on the ZCBF (7) to ensure the forward invariance of this approximated set does not guarantee the forward invariance of the actual safe set.On the other hand,while the actual safe set can be formed based on the real-time measurement of the state of the external agentz,its forward invariance requires knowing the entire trajectory of the external agent,which is not available,and it is impossible to design (7) to make the actual safe set forward invariant.However,as shown in Fig.1(b),if the control input is designed to assure the forward invariance of the intersection of the actual safe set and its approximation,which is contained in the actual safe set,the safety of the system is guaranteed.This shrinks the boundary of the approximated safe set to assure that it is contained in the actual safe set.Note that this set can be made forward invariant using (7) since the approximate knowledge of the state trajectory of the external agent is available through (8).As learning progresses and the external dynamics becomes more accurate,as shown in Fig.1(c),the approximated safe set becomes more accurate,and the system’s maneuverability improves.The faster the external dynamics converges,the faster the intersection of the approximated safe set and actual safe set expands.

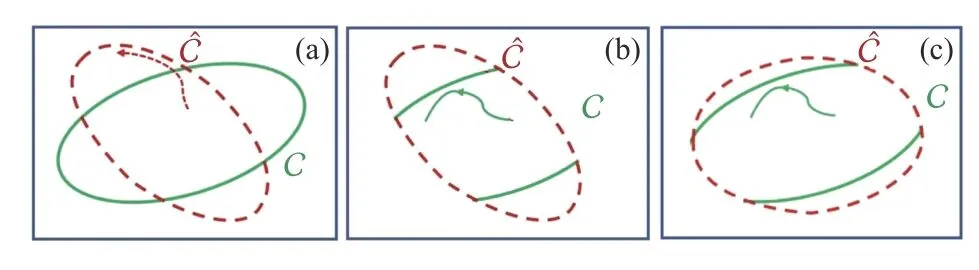
Fig.1.(a) With forward invariance of the ,strict safety boundary ofC might be violated.(b) Safety is ensured in common subset of and C.(c) By converging to C,more room of safe maneuver of the ego system is available.

In order to shrink the boundary of the approximated safe set and assure that it is contained in the actual safe set,the instantaneous sensory observations of the ego system fromzare used to form the actual safe set,and the intersection of the safe set and its approximation is derived accordingly.Ccis defined as the intersection of Cand

Before presenting the proposed approach,the following assumptions are made.

Assumption 1: Strict Interiority of the Initial Condition

The initial condition of the system (1) belongs to the interior of the safe set C.That is,

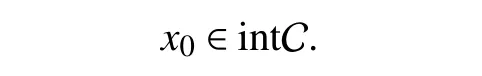
Assumption 2:The initial value of the approximated external dynamicssatisfies

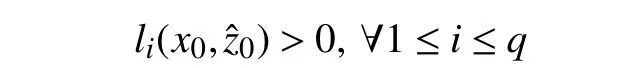
Remark 3:Considering (3) and (9),Assumptions 1 and 2 imply that Cc=∩C is non-empty.

Remark 4:Note that Assumptions 1 and 2 which state strict interiority of the initial condition and also its approximation,respectively,are mild and reasonable because if the initial condition is not safe,no controller can be designed to ensure safety in the future time.

Lemma 2:Consider Assumptions 1,2,and the setCldefined as

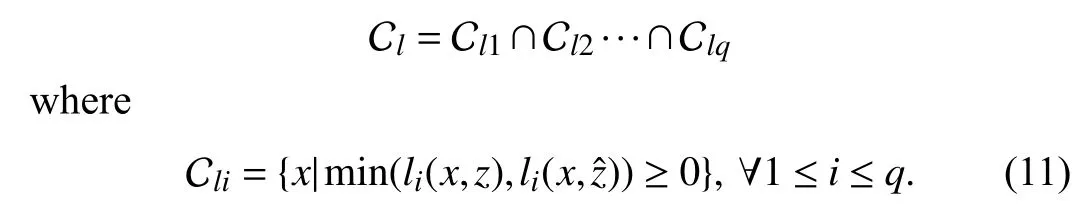
Then,Cl=Ccwhere Ccis defined in (10) as the intersection of sets Cand.

Proof:Given anyx∈X and 1 ≤i≤q,ifx∈Cl,from (11),one has

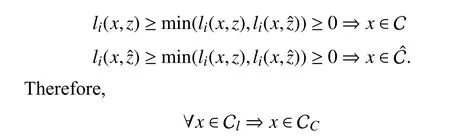
which means

On the other hands,ifx∈Cc

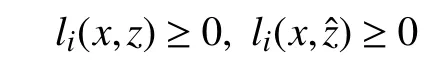
and therefore,

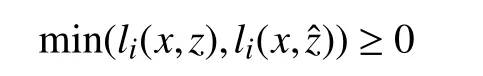
which implies

From (12) and (13),one has

The boundary of Ccis defined as

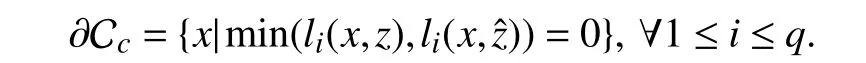
Definition 3:Given the control system (1),the smooth functionl=[l1,...,lq]∈C1is L-ZCBF for the set Ccif for each1 ≤i≤q

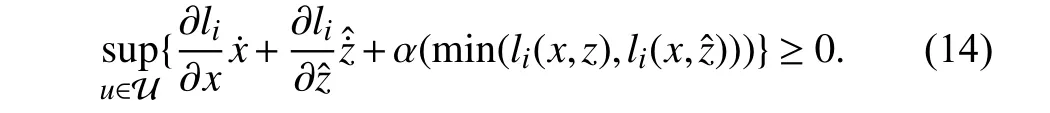
Moreover,the set of inputs that satisfy L-ZCBF condition is

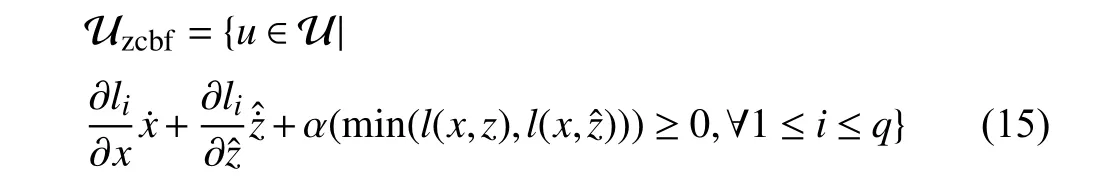
whereαis an extended class K funciton.

This definition is used to guarantee the safety of the system and forward invariance of Ccusing tangent cone of practical sets and the Nagumo’s theorem.

Definition 4: Practical Set (Definition 4.9 in [23])

Let O be an open set.Consider the set S1⊂O defined by a set of inequalities in the form of

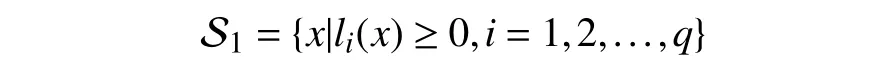
whereliis continuously differentiable function in O.The set S1is said to be a practical set if

1) For allx∈S1,there existsysuch that

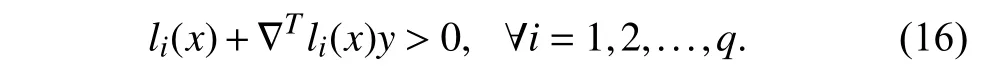
2) There exists a Lipschitz continuous vector field ψ (x) such that for allx∈∂S1(x),

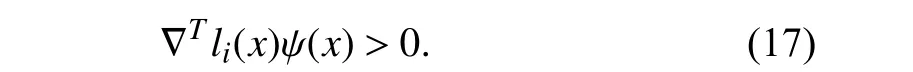
For allx∈∂S1,the tangent cone of the practical set is

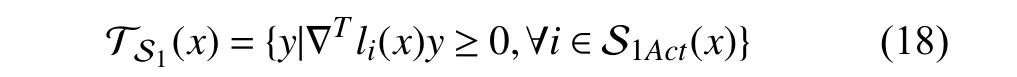
where S1Act(x) is the set of active constraints,which is defined as

For more details,see [23].

Theorem 2:Given the control system (1) and the setCc(10),any Lipschitz controlleru∈Uzcbfdefined in (15) ensures safety criteriali(x,z)≥0,∀1 ≤i≤q.

Proof:For each 1 ≤i≤q,ifli(x,z)≥li(x,),the L-ZCBF condition (14) becomes

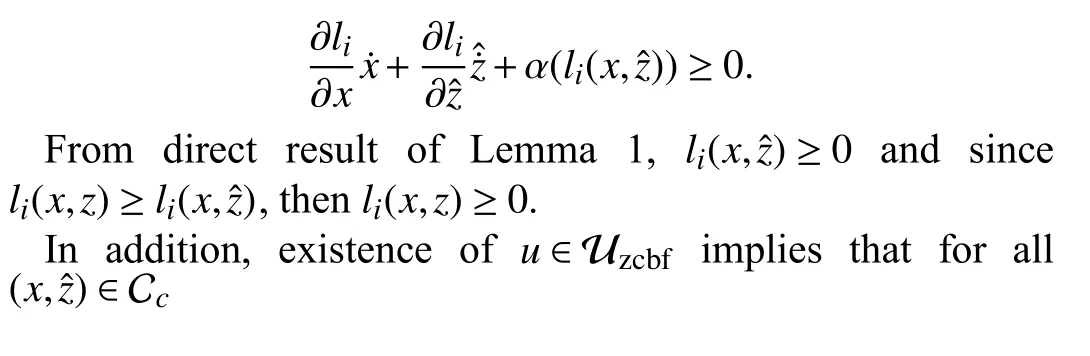
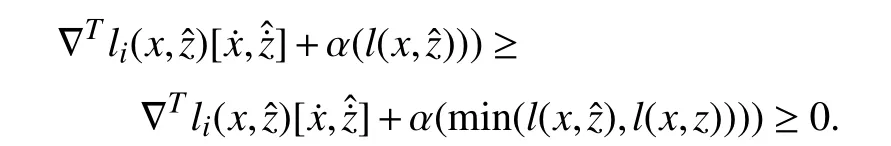
Therefore, (16) is satisfied.Ifli(x,z)＜li(x,), then L-ZCBF(14) turns to

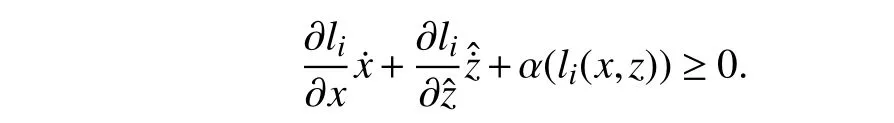
Thus, at the boundary of Ccin whichli(x,z)→0, one has

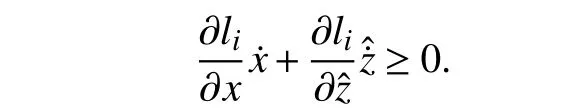
In other words,

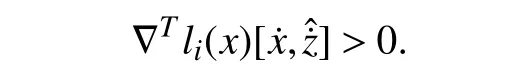
Therefore, (17) is satisfied for all (x,)∈∂Cc.Considering the definition of practical set and from (18), [] is within the tangent cone of Cc(11) as

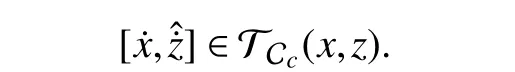
This implies that ifli(x,z)→0 , then () point inside the set at the boundary of Ccor in the worst case is tangent to the boundary.According to the Nagumo’s Theorem, Ccis forward invariant and since Cc⊂C, therefore, the approximated trajectories do not exceed the boundaryli(x,z)=0 implyingli(x,z)≥0 for allt＞0.Since this proof is valid for all 1 ≤i≤q, safety of the system is ensured.

Corollary 1:Given the control system (1), L-ZCBF introduced in (14) renders the intersection of the safe set and its approximation, Cc, forward invariant.

Proof:According to Theorem 2, boundary of the positive invariant set is shrunk to a more conservative value that provides a bigger margin to the safety boundary.According to Lemma 2, this forms the intersection of the safe set and its approximation.Therefore, the introduced L-ZCBF rendersCcinvariant indeed.■

Remark 5:The proposed L-ZCBF assures that at least a conservative safe set remains forward invariant, which guarantees safety.The conservativeness will be reduced next by presenting a fast and data-efficient learning approach for modeling the external agent.

Remark 6:It is shown that the external agent dynamics and,consequently, the unknown safe set are approximated using NNs.However, these approximations alone cannot be relied upon to ensure the forward invariance of the safe set.The reason is that the approximation might not be perfect and lead to exceeding the safety limits, which is not acceptable for safety-critical systems.Therefore, to design a more realistic and practical controller, the system observations and the approximated external agents dynamics are also combined with ZCBF.

Although the safety of the system can be guaranteed with an inaccurate model of the external dynamics, as learning enhances, the intersection set Ccexpands to the exact safe set Cand the system would be able to take less conservative control actions.In other words, employing a proper learning approach that suits the application boosts the control system’s performance.In the following subsection, the application of the experience replay method is demonstrated in this problem to identify the dynamical behaviors of external agents.This method provides a fast convergence of the network leading to the control system’s fast response, which is crucial in safetycritical applications.

B.External Dynamics Identifier

The motivation behind learning about the dynamics of external agents is to provide the ego system with a larger set of feasible actions and reduce the conservatism of the controller.In other words, enhancing the approximation of the safe set has higher importance compared to learning about the external agent states, and inspired by [27], an experience replay-based method is proposed which updates the identifier weights to reduce the set approximation error rather than the external state estimation error.Experience replay method uses recorded and stored data in the update law and provides fast convergence and an easy-to-check and verifiable the persistence of excitation (PE) condition, which is necessary to guarantee the convergence of the identifier weights.In contrast, online checking of this condition is generally difficult and even infeasible [27]–[30].

Considering (2) and (8), the external dynamics model is formulated into a filtered regressor form

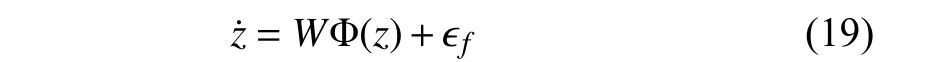
whereWand Φ are the weight matrix and the activation function, respectively.Also, ϵfis the model approximation error.

To convert the dynamics into the regressor form, letAzbe added to the both sides of (19), whereA=aIj×j,a＞0 selected basis functions.If the basis functions are chosen such that the unknown function dynamics is near the span of the basis functions, this error will be small.Note also that the boundedness of reconstruction error and its gradient are standard assumptions in neural network identification literature.Furthermore, using neural networks, the approximation guarantees are limited to a compact set.Since for safety-critical systems, the safe set is generally compact, and the system must not leave this set, therefore, approximation over a compact set is reasonable (Chapter 1 in [26]).

Lemma 3:Considering (20), (19) can be written as

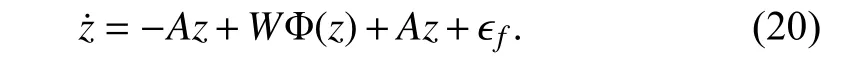
Assumption 3:There exists a constant 0 ＜ϵf*＜∞ such that

Note that ϵf*is unknown and depends on the quality of

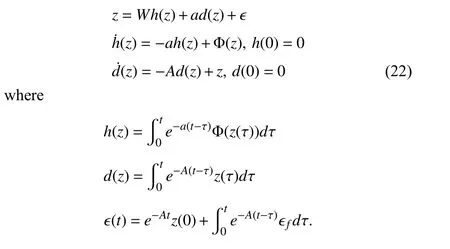
Proof:See Lemma 1 in [27].

Consider identifying weight estimator as

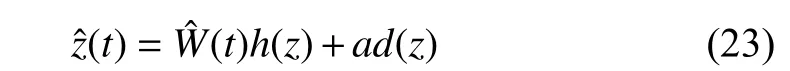
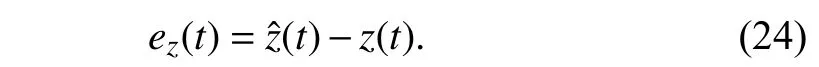
By considering (22)–(24),one has the state estimation error as

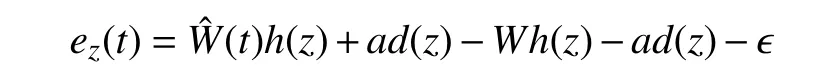
which is simplified to

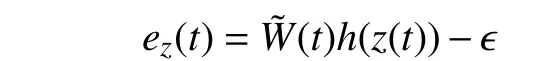
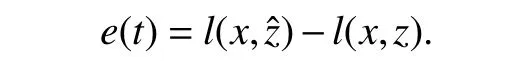
By using the Taylor expansion around (x,z) and some manipulations,one has

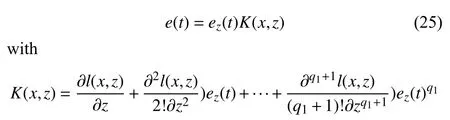
whereq1is the maximum degree ofzinl(x,z).The derivatives with the order of higher thanq1+1 are zero and eliminated from the Taylor expansion.

In experience replay method,recorded samples are used in the update law.Define the state estimation error using thekth sample as

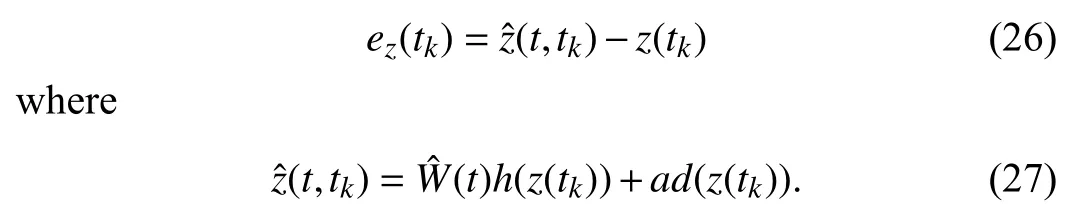
Using (22) and (27),the error defined in (26) becomes

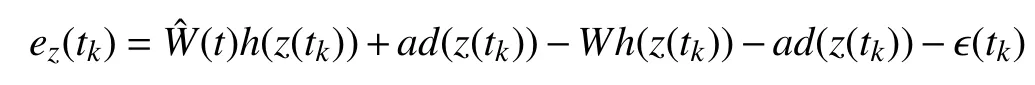
which further is simplified to

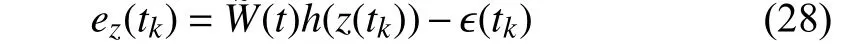
and the set estimation error at thekth sample is defined accordingly as

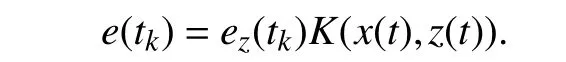
The update law is then given as

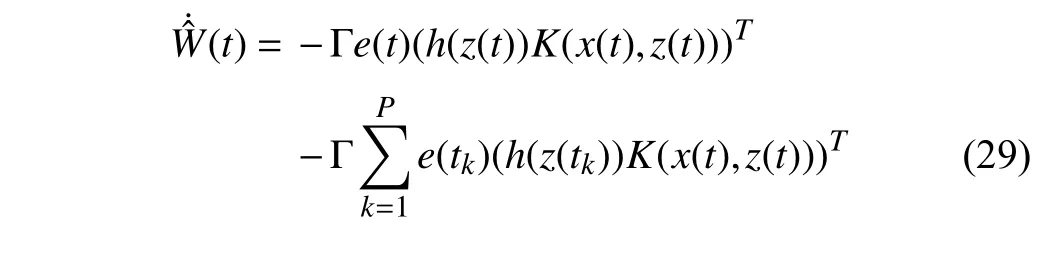
wherePis the overall number of stored data and Γ is a positive-definite matrix which determines the learning rate.Let the matrix of stored data be

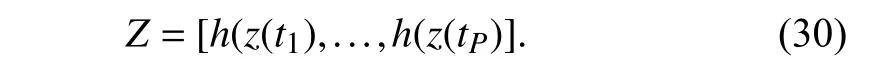
Then,the persistence of excitation condition is defined as

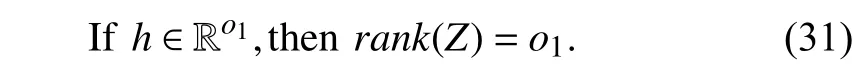
Remark 7:Using the history of data in the experience replay approach makes learning the safe set fast and data-efficient.This is of vital importance for safety-critical systems operating in an uncertain environment since the learning phase and operation phase in these systems are not separated.Therefore,control approaches with fast convergence capability in the learning process make control of safetycritical systems more practical.

Remark 8:Adaptive optimal control schemes require a PE condition to ensure the sufficient exploration of the state space.An exploratory signal consisting of sinusoids of varying frequencies can be added to the control input to ensure PE qualitatively.Note that the requirement of rank satisfaction is much less restrictive than the standard PE condition requirement and is much easier to verify online.The exploratory noise can be removed as soon as the rank condition is satisfied,which can be easily certified.

Theorem 3:Consider the model (19),the update law (29)and assume full rank of the matrixZin (30): 1) If there is no reconstruction error,i.e.,ϵf=0,then the set approximation error (28) converges to zero exponentially fast.2) If ϵf≠0,then the set estimation error is uniformly ultimately bounded(UUB),and the ultimate bound can be made small by recording rich data in the history stack.

Proof:Let the Lyapunov function on weight error be as

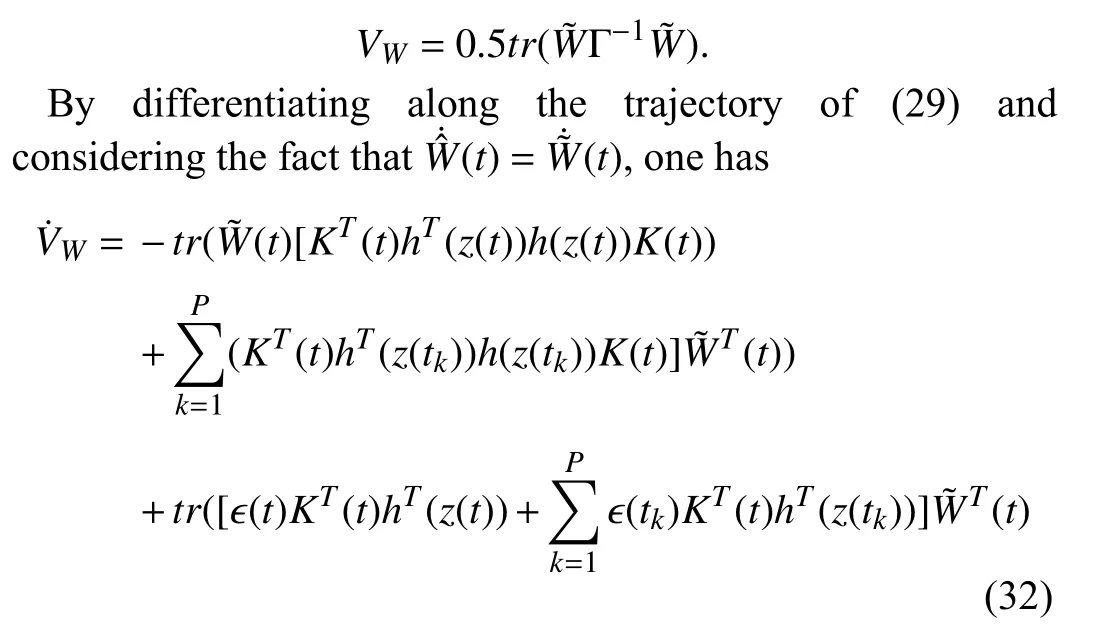
whereK(t) stands forK(x(t),z(t)).Equation (32) is simplified as

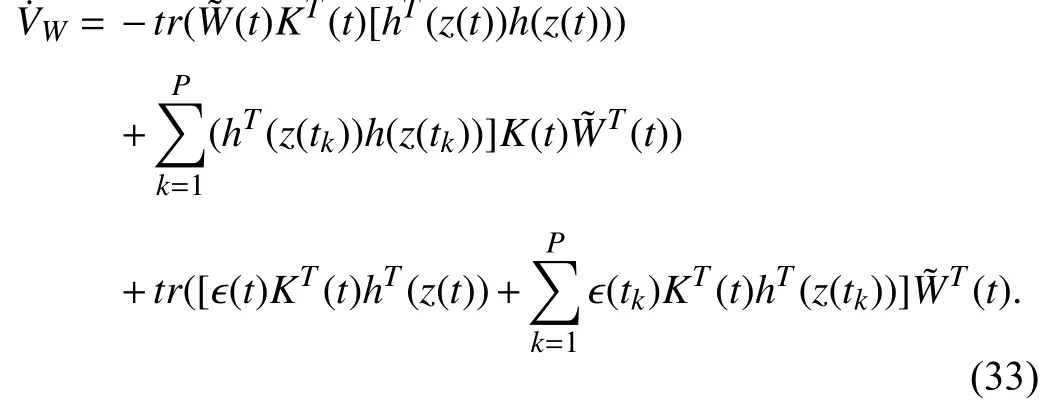
If the rank condition onZholds,then

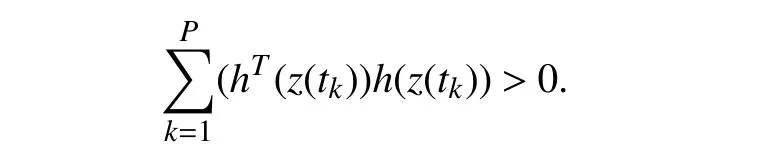
Therefore,for case of no reconstruction error,＜0 me ans thatexponentially convergesto0.This completes the first part of the proof.For the second part and under reconstruction error,assume

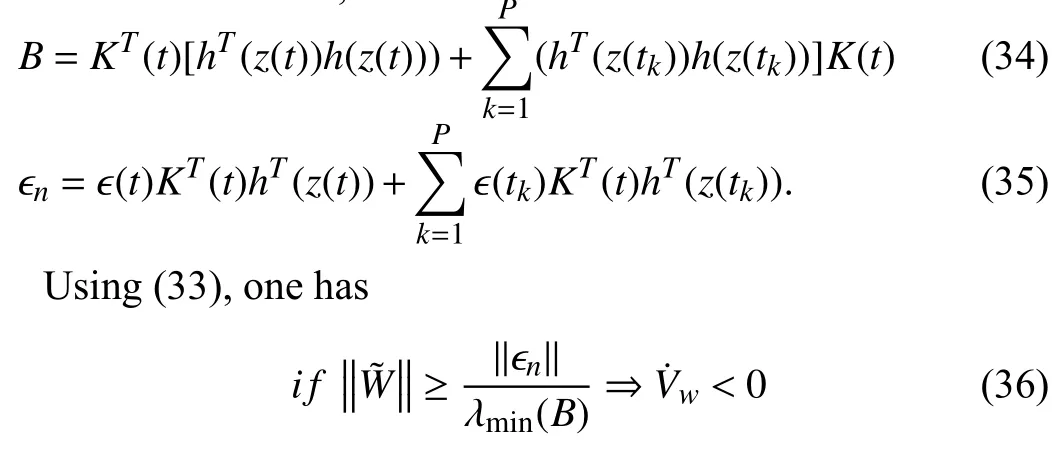
where λminis the small esteigen value ofBdefinedin(34).Therefore,if ϵf=o,W˜ converges to zeroexponentially fast and thuse(t) in (25) converges to zero exponentially fast.

According to (19),(21),(22),and (35),one has

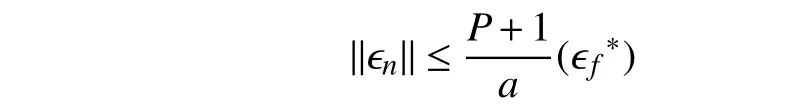
where by proper selection ofaas identifier design parameter,(36) is satisfied.For any value ofa,is negative outside of the following compact set:

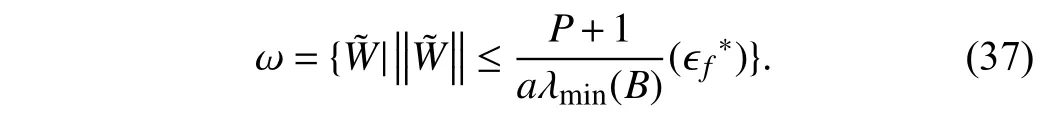
Basedon(25),e(t)will alsore main bounded,and this com pletes the proof of the second part of the theorem.

Remark 9:Note that the proposed set identification method provides exponential convergence of the set approximation error to zero.This implies that there are timest1,t2,...during learning that set approximation errore(tk)=l(x(tk),(tk))-l(x(tk),z(tk)) has decreased i.e.,e(tk+1)＜e(tk).Considering the approximated safe set at this sequence{x(tk)|l(x(tk),(tk))≥0} which is equivalent to the set{x(tk)|l(x(tk),z(tk))≥-e(tk)}reveals that by decreasing the error,the approximated set gets closer to the exact safety set C.Utilizing experience replay technique has at least two advantages: 1) it significantly improves the decay rate of the approximation error and thus reduces the conservatism,and 2) it provides the ego system with an easy-to-verifiable metric to check if the approximated safe set converges to the actual safe set.

Remark 10:Fast convergence of the model enables the control system to act in a less conservative manner leading to enhanced performance.Even in the case of an inaccurate model with a non-zero reconstruction error,this method provides an acceptable performance with a UUB weight estimation error.

IV.CONTROL FRAMEWORK

The proposed control framework is demonstrated in Fig.2.First,the control system gathers data,e.g.,distance from other agents in the environment collected by camera or LIDAR sensor,by observing its surrounding environment.The observed data are labeled as risky and safe,respectively.The safe data coming from the external agents that do not impose any risk on the control system are removed from the collected data.Then,the risky data representing external agents that can impose risk on the control system are applied to identifier blocks that approximate the dynamics of risky external agents using the modified experience replay method.Next,the state of the system and the output of identifier modules are injected into the CBF block to form L-ZCBF constraints according to the strict safety criterion.Finally,these L-ZCBF constraints govern the performance of the controller block,and control action must satisfy L-ZCBF constraints.The combination of identifier networks and the CBF block is called the guardian block.

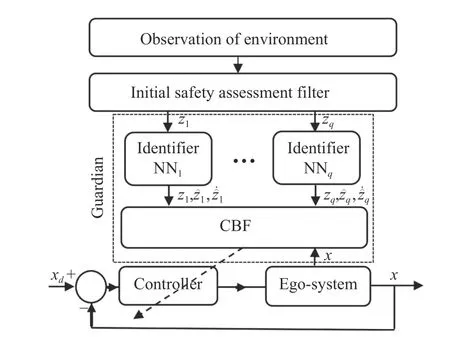
Fig.2.Control scheme.

The quadratic programming [1],[2] is employed to design the controller for this platform.The performance objective is formulated as a soft inequality constraint on derivative of the Lyapunov function.This constraint on the Lyapunov function and ZCBF constraint are unified by imposing them as constraints of quadratic programming problem,which aims to minimize a cost function.The cost function is a combination of the control inputuand the relaxation factorηwhich is considered in the performance objective to make it a soft constraint.As a result,the minimum value of the control input,which satisfies safety is obtained and the system gets close to desired performance as much as possible.ZCBFbased quadratic programming is formulated as

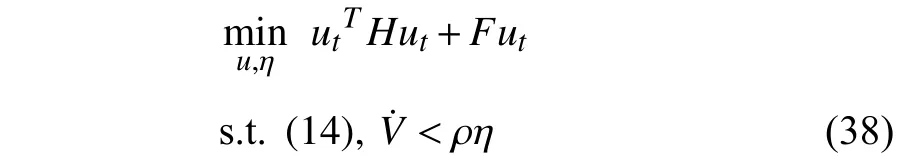
whereut=[u,η],HandFare the weight matrices,Vis the Lyapunov function andρis the coefficient of the relaxation factorη.

Remark 11:If optimal controlleru*for performance objective is available,such as linear quadratic regulator(LQR) solution in a linear control system,then,the Lyapunov inequality in (38) can be replaced by equalityu=u*+ρη.

The overall algorithm is as follows.

V.CASE STUDY

The effectiveness of the proposed approach is verified here by designing a safe maneuver controller for an autonomous vehicle in the presence of other vehicles on the road.

A.Control Scenario

Fig.3 shows a safety-critical maneuver for autonomous vehicles in an urban area.The ego vehicle,specified by its position (xe,ye),is traveling in the road,and the control objective is to reach a pre-defined destination,which is marked in Fig.3,in an optimal manner.However,the road is shared with other vehicles with uncertain behaviors,and their objectives might be in conflict with the ego vehicle desired objective.Vehicle (x1,y1) is traveling next to the ego vehicle;although it is very close,it looks safe.Vehicle (x2,y2) was not previously observable to the ego vehicle while it is now reaching the cross-section and might impose risk on the ego vehicle passing the crossroad.Vehicle (x3,y3) is farther but,it is moving in the same path as the ego vehicle and might impose risk on its maneuver in the future time.These types of maneuver scenarios are practically challenging but so common in everyday driving.This even becomes more challenging if instead of vehicles,bicycles or pedestrian are in the road which add more unpredictability and complexity to the control scenario.To elaborate on that,the effect of having an agent with a more complicated behavior instead of vehicle three is investigated as well.The following section mathematically formulates this scenario.

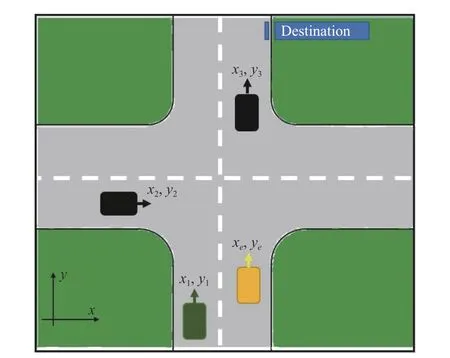
Fig.3.Control scenario.

B.Mathematical Representation

The simple mass point model for vehicles is used [20].

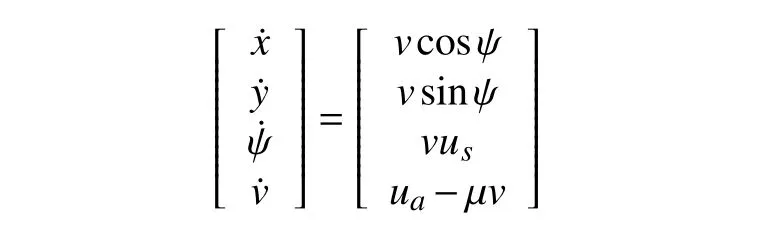
wherex,yare cartesian coordinate of the vehicle,vstands for vehicle’s velocity andψis the heading angle of the vehicle.usis the steering angle anduais acceleration.μis the friction coefficient.For simplicity,the state vector is presented byX=[x yψv].When moving in a straight line with zero friction coefficient,the dynamics of the ego vehicle and vehicles 1 and 3 are simplified as a double integrator

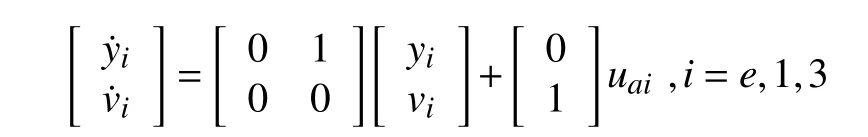
and the dynamic of vehicle 2 is given as

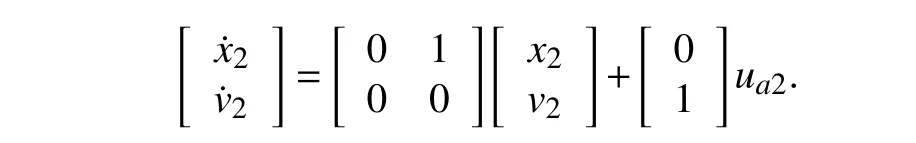
Note that although the open-loop system is unstable,its controllability matrix is,which is full rank.Therefore,the system satisfies the stabilizability assumption,and there is a control input to make the closed-loop system stable.As explained in Algorithm 1,after gathering observation data,an initial safety assessment is required.In this scenario,using distance to assess safety is not functional since vehicle one is close to the ego vehicle,but it is safe.However,other vehicles are far from the ego vehicle,but they might impose risk on it.Therefore,the minimum distance of surrounding agents to the center of the road that the ego vehicle is moving along is considered for initial safety assessment and is named as the minimum safe lateral distancermin.In this scenario,rminis inx-coordinate defined asxmin,which is defined to be the lane width here and can be modified based on the application.As a result,if surrounding agents are within this range,they will be considered risky.Therefore,vehicle one is safe and will not be included in the loop as long as its lateral distance is in the safe range.However,other agents are considered risky,and headway safety criteria are applied to the guardian block regarding them.Headway rule stated in [1],[31] is employed

whereveis the ego vehicle speed,andDis the distance between two vehicles.Then,the safety criteria for vehicles 2 and 3 in this scenario would be

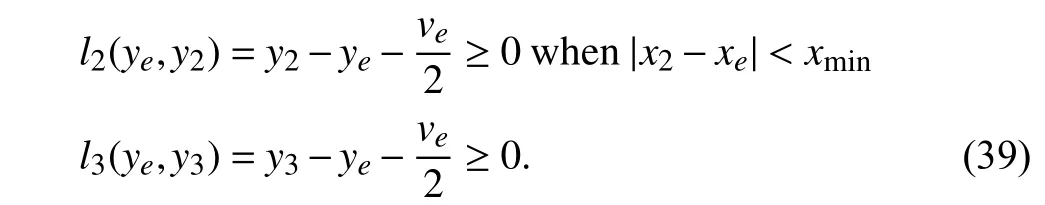
This formulation shows that if any vehicle gets very close to the lane that the ego vehicle is moving,then a minimum headway is required.Therefore,if the distance between the ego vehicle and any other vehicle gets shorter,the ego vehicle should decline its velocity to operate under these safety criteria.

The ego vehicle observes the identified external agents as black boxes in which only their current states are measurable.Thus,the identifier NNs for vehicles 2 and 3 are defined as

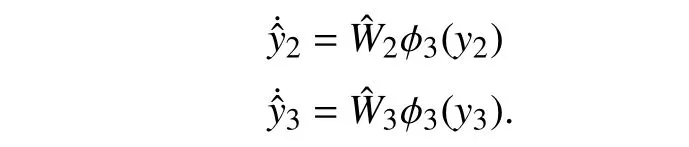
The ego vehicle identifies the dynamics of vehicle 2 only inycoordinate becausexis only needed for initial assessment,and it is not included in the headway criterion.

One of the advantages of the proposed approach is that safety is ensured even with inaccurate modeling of the external agents.Thus,to reduce computational cost and learning time,simple single layer perceptron with polynomial activation functions are employed as

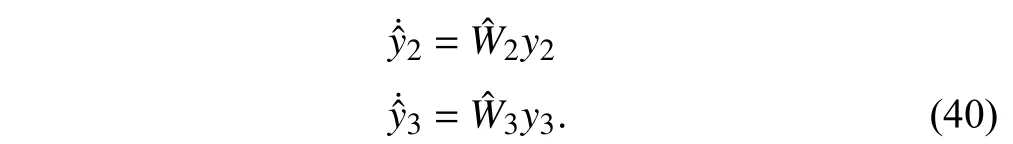
Remark 12:Since vehicle 2 is crossing the lane,the corresponding identifier is activated after it becomes observable for the ego vehicle.However,the corresponding LZCBF is formed and incorporated in quadratic programming when it reaches the lane that the ego vehicle is moving in.This setup can be adjusted based on the application.For example,one might decide to design a more conservative controller and incorporate the L-ZCBF at the time of observation.

L-ZCBFs are defined using (14) and (39) as

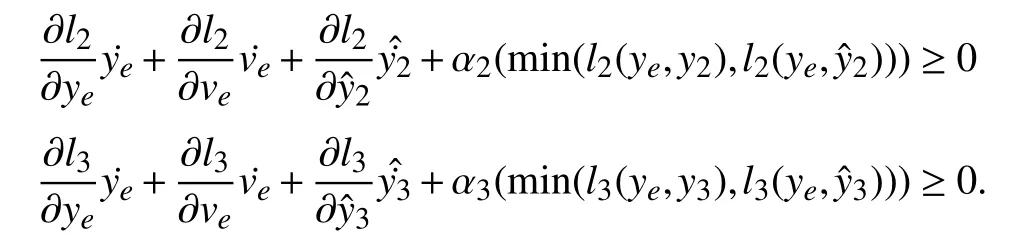
For the performance purposes,LQR problem is solved as mentioned in Remark 11.Then,the overall controller is performed using Algorithm 1.The values of parameters used in the simulation can be found in Table I.

TABLE ITHE VALUES OF PARAMETERS USED IN THE SIMULATION

VI.SIMULATION RESULTS

Simulation is performed for the aforementioned control scenario in three sub-scenarios.First,an accurate network model with zero reconstruction error is employed which can converge to the exact vehicle model.In the second subscenario,an inaccurate model is used,which cannot converge to the exact model.The third sub-scenario adds more complexity by considering an agent with a more complicated behavior in front of the ego vehicle,which the employed NN cannot accurately model.The purpose of using an inaccurate model is to demonstrate the strength of the proposed approach in guaranteeing safety in case of modeling error.

1) Zero Modeling Error Scenario:The network defined in(40) is assumed to be accurate without any reconstruction error,so after learning its weights,it converges to the exact model.Fig.4 shows the results,whereyas coordination of the ego vehicle and two risky vehicles 2 and 3 are demonstrated.Without loss of generality,the destination of the ego vehicle is assumed to be located at the origin.The ego vehicle starts from its initial position,but a crossing vehicle is reaching,so the ego vehicle slows down and proceeds in a smooth maneuver when the crossing vehicle passes.After passing the crossroad,the ego vehicle faces another slow-moving vehicle in front of it; as a result,it slows down to adapt to the flow of traffic.As can be seen in Fig.4,because of the presence of vehicle 3,the ego vehicle could not reach the destination; but,it reached as close as possible while safety is still ensured.Fig.5(a) shows the convergence of the weights of networks.The LQR performance of the system in lack of safety considerations is demonstrated in Fig.5(b).As can be seen in this figure,without safety consideration,the ego vehicle would crash with either vehicle 2 or vehicle 3.To further clarify the advantage of employing the proposed learning method,a simulation is conducted to compare the weight convergence with and without using the past stored data in the update law as depicted in Fig.6.As seen in this figure,the network weight has a fast and exponential convergence under the proposed method.

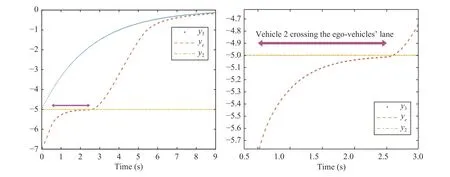
Fig.4.Position of vehicles in “y” coordinate (Scenario 1).

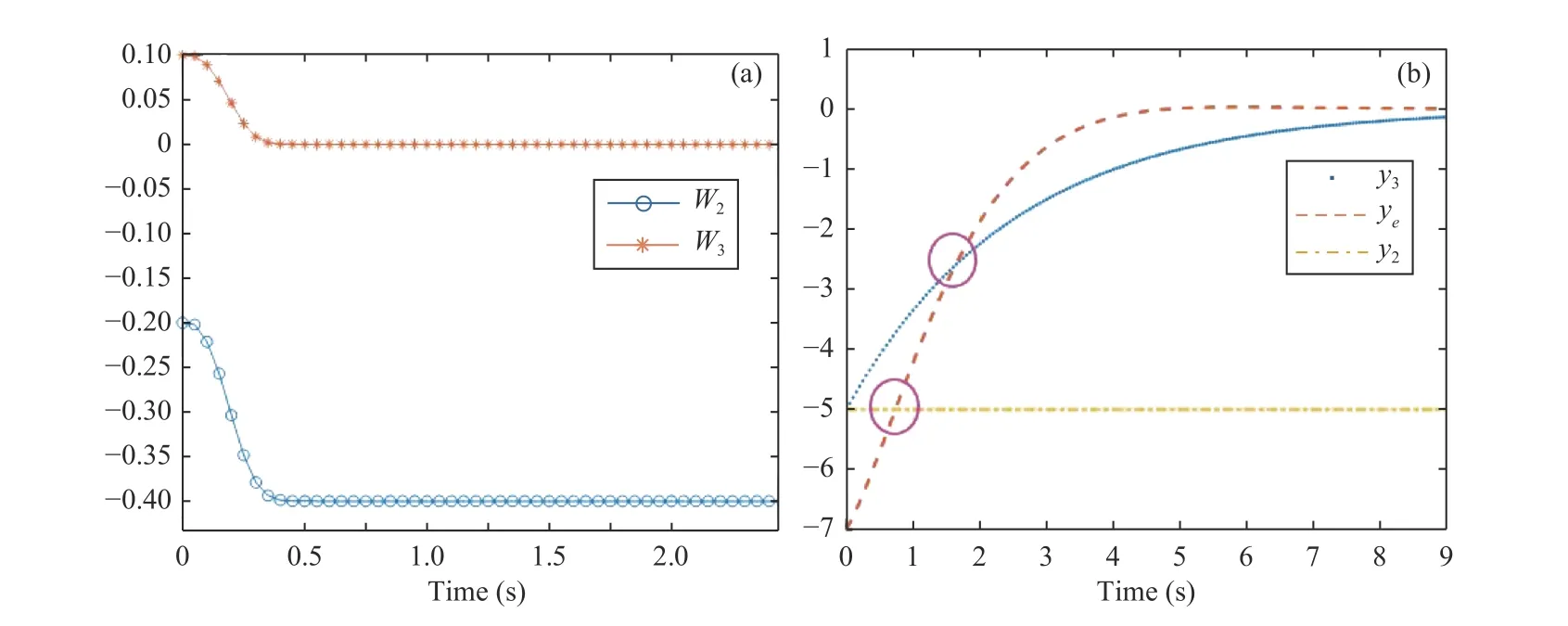
Fig.5.(a) NN weights (Scenario 1); (b) Optimal solution without safety consideration.

2) First Non-Zero Modeling Error Scenario:In this subscenario,the same network as (40) is employed while vehicle 3 demonstrates a different behavior as=a.In other words,the allocated network is not a proper one for modeling the dynamics of vehicle 3.Fig.7 shows the convergence of both networks’ weights.As can be seen,W3could not converge.Fig.8 shows the locations of the ego vehicle and vehicles 2 and 3 in this scenario.Despite inaccurate modeling,the safety of the system is ensured.The ego vehicle slows down to avoid crash with vehicle 2,and after that,it accelerates to reach the destination.However,it has faced vehicle 3 and has adjusted its velocity accordingly until it gets to the destination safely.

3) Second Non-Zero Modeling Error Scenario:One of the big challenges of safe urban driving is unpredicted and hardto-model dynamics such as the jump of an animal to the road or human behavior.The proposed method is functional in handling these unpredicted behaviors.To further analyze the result of employing this method,an agent with a more complicated dynamics is considered to be the only risky agent which is moving in front of the ego vehicle with dynamics of

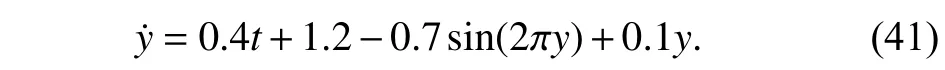
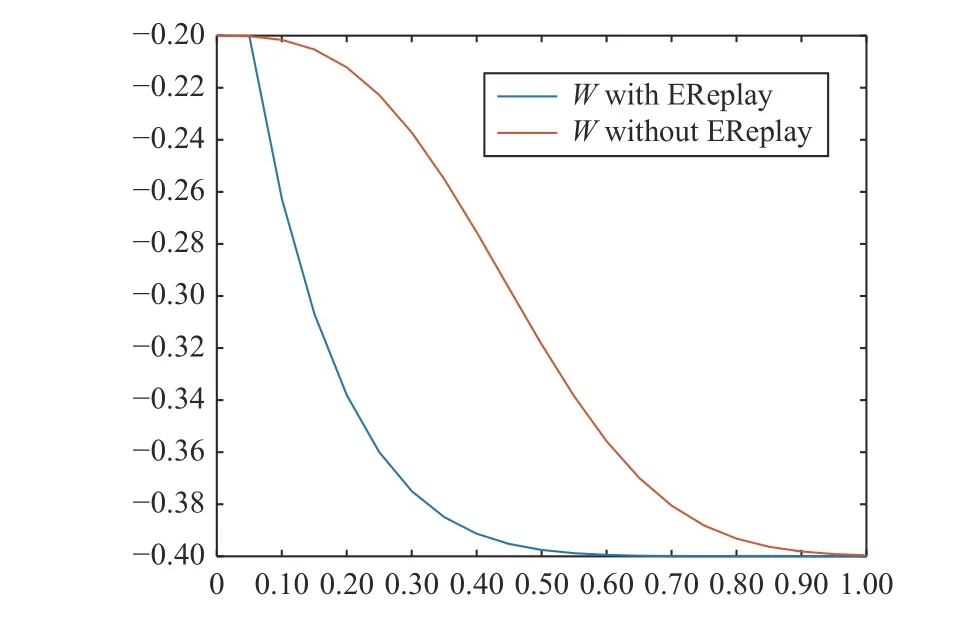
Fig.6.NN Weights with and without experience replay.

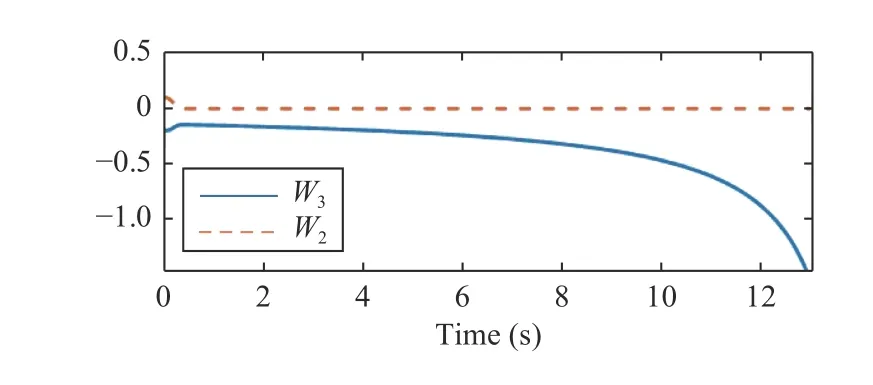
Fig.7.NN weights (Scenario 2).

The network (40) is employed for the identification of this dynamics,which has non-zero reconstruction error.The network weight update is shown in Fig.9 which could not converge.They-coordinate of both agents is shown in Fig.10.As can be seen in this figure,despite the complexity in the behavior of the external agent and the existence of reconstruction error,the ego vehicle has a safe maneuver.

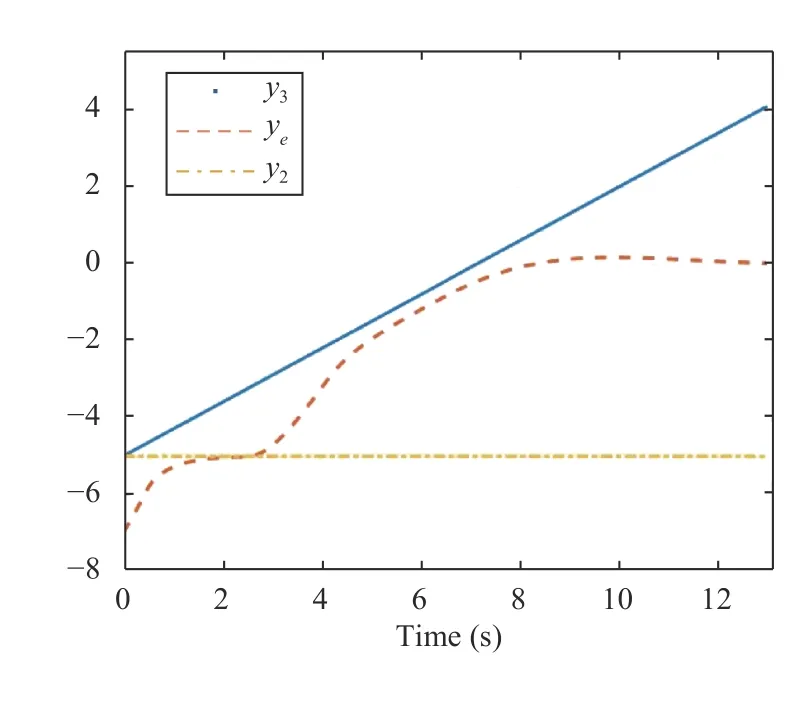
Fig.8.Position of vehicles in “y” coordinate (Scenario 2).

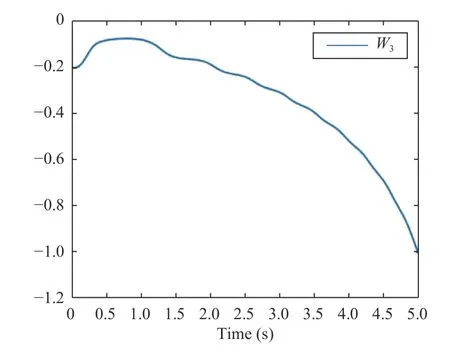
Fig.9.NN weight (Scenario 3).

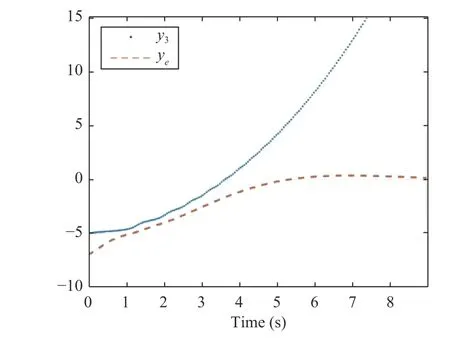
Fig.10.Position of agents in “y” coordinate (Scenario 3).

Remark 13:The purpose of this simulation is to demonstrate the capability of the method for guaranteeing safety in case of facing an agent whose dynamics cannot be modeled using predefined networks.

A.Discussion

The efficacy of the proposed method is examined in three different scenarios: 1) The assigned NN properly captures the dynamics of the external agent,but safety and performance are in conflict.It is shown that the agent has a safe maneuver during and after learning and gets close to its destination as far as it is safe.2) There exists a reconstruction error,and the assigned NN cannot fully capture the dynamics of the external agents.It is shown that despite this error,the ego-vehicle still maintains a safe maneuver.This is of significant applicability since,in many real applications having an NN that fully captures the unknown dynamics is not always possible or tractable therefore,usage of a simplified model is facilitated.3) A more complicated dynamical behavior in the presence of reconstruction error is considered in this scenario.It is shown that despite complex dynamics,still the safety of the egovehicle is ensured.

VII.CONCLUSION AND FUTURE WORK

In this paper,a learning-enabled ZCBF controller for safetycritical systems under uncertainty has been proposed.It has been proved that the proposed method is capable of ensuring safety in complicated and uncertain environments in the presence of external agents with unknown dynamics.It has been also demonstrated that safety during learning and even with inaccurate modeling of external agents is guaranteed.As a result,this approach has provided a practical method in control scenarios that accurate modeling needs a great number of data and computationally expensive learning schemes while still un-predicted objects are expected such as autonomous driving in an urban area.Meanwhile,having a better model has enabled the controller to take a less conservative action and has resulted in a better performance.To achieve this goal,a modified experience replay method has been proposed that identifies the external agents dynamic to minimize the difference between the safe set and its approximation.This method provides fast convergence and ensures a bounded error to the exact model even with inaccurate modeling which are both crucial in safety-critical control systems.Future work includes consideration of disturbance in the ego system’s dynamics and extension to a robust framework.Furthermore,the reciprocal behavior of agents in the environment can be considered.