Cubature Kalman Filter Under Minimum Error Entropy With Fiducial Points for INS/GPS Integration

Lujuan Dang,Badong Chen,,Yulong Huang,,Yonggang Zhang,,and Haiquan Zhao,

Abstract—Traditional cubature Kalman filter (CKF) is a preferable tool for the inertial navigation system (INS)/global positioning system (GPS) integration under Gaussian noises.The CKF,however,may provide a significantly biased estimate when the INS/GPS system suffers from complex non-Gaussian disturbances.To address this issue,a robust nonlinear Kalman filter referred to as cubature Kalman filter under minimum error entropy with fiducial points (MEEF-CKF) is proposed.The MEEF-CKF behaves a strong robustness against complex non-Gaussian noises by operating several major steps,i.e.,regression model construction,robust state estimation and free parameters optimization.More concretely,a regression model is constructed with the consideration of residual error caused by linearizing a nonlinear function at the first step.The MEEF-CKF is then developed by solving an optimization problem based on minimum error entropy with fiducial points (MEEF) under the framework of the regression model.In the MEEF-CKF,a novel optimization approach is provided for the purpose of determining free parameters adaptively.In addition,the computational complexity and convergence analyses of the MEEF-CKF are conducted for demonstrating the calculational burden and convergence characteristic.The enhanced robustness of the MEEF-CKF is demonstrated by Monte Carlo simulations on the application of a target tracking with INS/GPS integration under complex non-Gaussian noises.

I.INTRODUCTION

THE global positioning system (GPS) [1] and inertial navigation system (INS) [2],[3] provide the complementary function for position and attitude determination of moving objects.The integrated INS/GPS receives the increasing attention due to the availability and accuracy[4]–[7].At present,the INS/GPS integration is performed by the Kalman filters [8],[9] such as extended Kalman filter(EKF) [10]–[13],unscented Kalman filter (UKF) [14],[15],cubature Kalman filter (CKF) [16]–[22],etc.[23],[24].Especially,the CKF is a preferable filtering approach for nonlinear systems due to its higher precision than EKF and UKF and moderate computational cost [25].The aforementioned nonlinear Kalman filters are associated with the optimization of the minimum mean square error (MMSE) and provide potentially superior performance under Gaussian assumptions [26].

However,the integrated INS/GPS system in practice is often confronted with non-Gaussian noises,such as impulsive disturbances and multi-modal distribution,etc.,resulting in a much degraded performance of CKF [17]–[21],[24],[27]–[35].Robust methods are therefore recommended for nonlinear Kalman filtering under non-Gaussian noises such as the robust student’s t based Kalman filter (RSTKF) [28]–[30],Gaussian sum filter (GSF) [27],particle filter (PF) [24],cubature particle filter (CPF) [31],and improved cubature Kalman filter (ICKF) [32].In particular,the RSTKF utilizes a Student’s t distribution to model heavy-tailed non-Gaussian noises for yielding a robust posterior estimate [28].The GSF and PF employ a set of Gaussian mixture distributions and rule-based particles to approximate the posterior distribution,respectively [24],[27].The CPF combines the features of the CKF and PF [31].The ICKF adopts the novel sigma-points update method to improve the robustness of CKF [32].These Kalman filters can effectively reduce the adverse impact of non-Gaussian noise,but usually involve the calculation of multi-dimensional integrals.When faced with a more complicated distribution,these filters may be difficult to obtain an accurate approximation for posterior distribution and the estimation performance will not be further improved.

Apart from above filtering approaches,there exist nonlinear Kalman filters based on solving multi-dimensional optimization problem.Robust optimality criteria are therefore used in developing the robust CKFs for robustness improvement,which is more flexible and simpler than approximating the posterior distribution.For example,the Huber-based cubature Kalman filter (HCKF) [36] and its square-root version [37] are all derived by minimizing the piece-wise Huber function.Recently,the maximum correntropy criterion (MCC) [38]–[41] has also been applied in CKF and its square-root version,generating maximum correntropy cubature Kalman filter (MCCKF) [42] and maximum correntropy square root cubature Kalman filter(MCSRCKF) [25],respectively.Although the MCC-based CKFs exhibit improved filtering precision in comparison with the MMSE-based CKFs and even Huber-based CKFs [25],[41],the MCC-based CKFs still cannot perform well under more complex non-Gaussian noises especially characterized by a multi-modal distribution noise.

Compared with MCC,the minimum error entropy (MEE)criterion [43]–[45] exhibits better robustness due to the well modelling ability of the error entropy [26] under the framework of information theoretic learning (ITL).Recently,the MEE-based Kalman filter (MEE-KF) and MEE-based extended Kalman filter (MEE-EKF) have been derived for handling complex non-Gaussian noises like multi-modal distribution noises [46].However,there still exist issues to be solved in MEE-KF and MEE-EKF.For example,the MEEEKF has limited filtering accuracy for dynamic estimation of a nonlinear system since the MEE-EKF is derived by linearizing a nonlinear function.In addition,a bias may be required to remove the error mean in MEE-KF and MEE-EKF to locate an optimal solution [44].The MEE-based Kalman filters are all confronted with the choice of free parameters.To solve these issues,this paper aims to develop a robust nonlinear Kalman filter,called cubature Kalman filter under minimum error entropy with fiducial points (MEEF-CKF) to deal with the complex non-Gaussian noises such as large outliers and multimodal distribution noises.The contributions of this work are summarized as follows:

1) The MEEF-CKF is developed by applying the minimum error entropy with fiducial points (MEEF) to CKF,where the MEEF can automatically locate the peak of the error probability density function (PDF) at zero and is beneficial for robustness enhancement.

2) A novel optimization approach is presented for determining the free parameters of MEEF-CKF adaptively.

3) The complexity of MEEF-CKF is analyzed in detail,which indicates an acceptable burden in comparison with traditional Kalman filters.In addition,a sufficient condition is provided for ensuring the convergence of the fixed-point iteration in MEEF-CKF.

4) The novel MEEF-CKF is applied for target tracking with the INS/GPS integration under different non-Gaussian noises.Simulation results have demonstrated the robustness of MEEF-CKF and the effectiveness of parameter optimization.

The rest of the paper is organized as follows.In section II,we briefly review CKF and MEEF.Section III presents the proposed MEEF-CKF where multiple free parameters are chosen by a designed optimization method.Section IV provides the computational complexity and convergence analyses.Section V shows simulation results of target tracking with INS/GPS integration.The conclusion is given in Section VI.

II.RELATED WORK

A.Cubature Kalman Filter

Consider a nonlinear discrete-time dynamic system

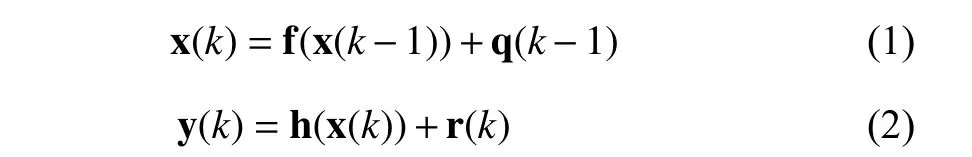
where x(k)∈Rnand y(k)∈Rmrepresent state and measurement vectors at discrete timek,respectively; f(·) and h(·)are state transition and measurement functions,respectively; q(k-1)∈Rnand r(k)∈Rmdenote zero mean process noise and measurement noise with covariance matrices Q(k-1) and R(k),respectively.Define the state estimation atk-1 by(k-1) and its corresponding error covariance matrix P(k-1)=S(k-1)ST(k-1) whereS(k-1)represents the Cholesky decomposition of P(k-1).The CKF is a preferable choice of dynamic estimation due to its desirable accuracy and moderate computational cost.The CKF performs the state estimation by two steps,i.e.,prediction step and update step.

1) Prediction Step:Calculate sample points ξi(k-1) by

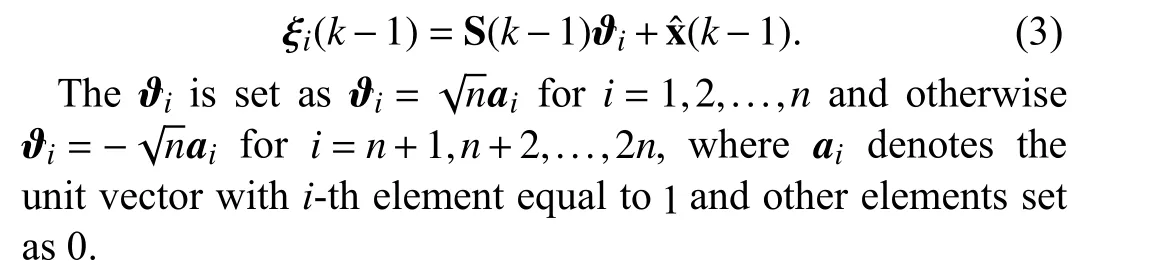
Compute the propagated cubature points

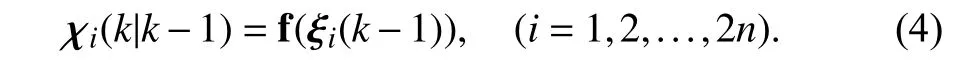
Calculate the predicted state(k|k-1) and its corresponding covariance matrixPxx(k|k-1)

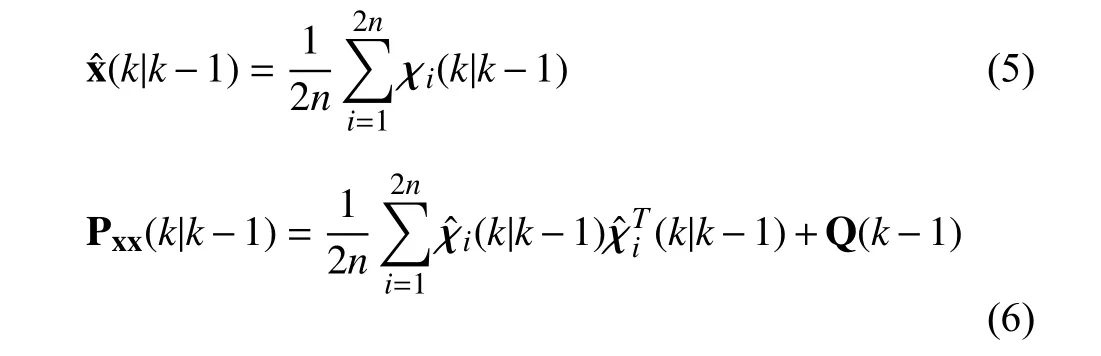
2) Update Step:Calculate sample points ξi(k|k-1) by

where S(k|k-1) is the Cholesky decomposition of Pxx(k|k-1).Calculate the transformed cubature pointsγi(k)by

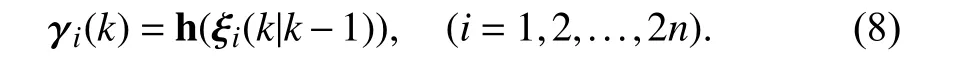
Calculate the predicted measurement(k|k-1),its corresponding covariance matrix Pyy(k|k-1) and the state-measurement cross-covariance matrix Pxy(k|k-1) by

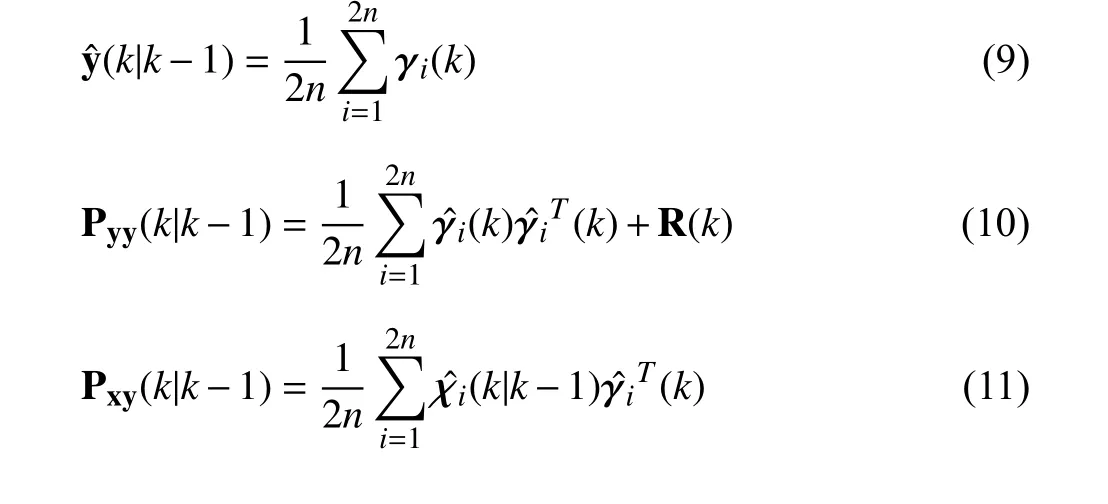
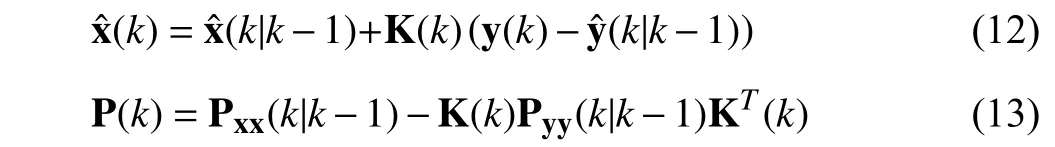
where the gain matrix K (k) is defined as

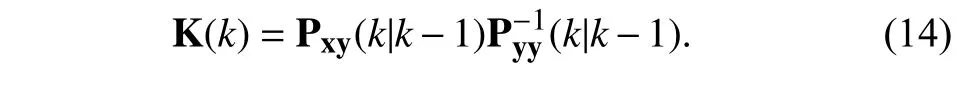
B.Minimum Error Entropy Criterion With Fiducial Points

In ITL,the entropy is a preferable tool for modelling error distribution.For the error variableewith the probability density function (PDF)pe(·),the Renyi’s quadratic entropy is defined by [44]

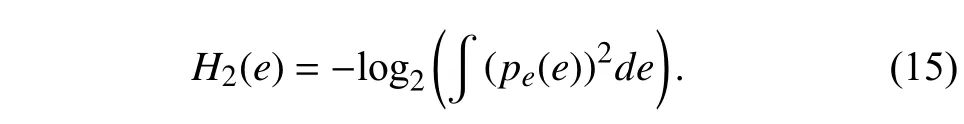
The MEE is derived by minimizing (15) which is equivalent to maximizing

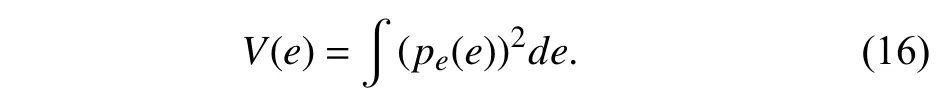
Since thepe(e) is unknown in practice,the Parzen’s estimator is used for estimating the PDF by using samples,i.e.,

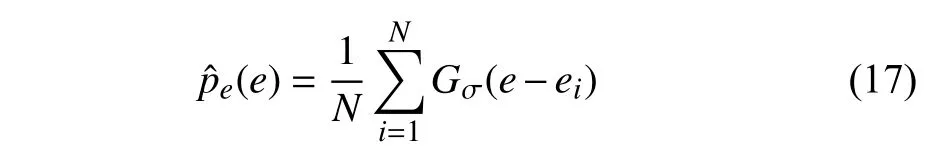
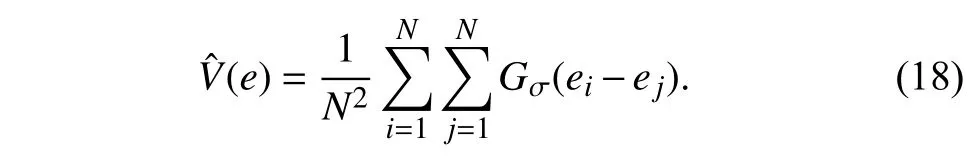
Since MEE in (18) only focuses on minimizing differences among errors,errors may not be located at zero after optimization.For solving this issue,the traditional method sets manually the bias for the model to yield zero mean error.Here,to automatically set the bias,one can construct an augmented error form asE[e0,e],wheree0=0 serves as a fiducial point and e=[e1,e2,...,eN] denotes the error samples[26],[47].When the augmented error is considered in (18),we obtain the minimum error entropy with a fiducial point at zero by maximizing

By neglecting constantsGσ(0) and 1/(N+1)2in (19),the MEEF is obtained by maximizing

Equation (20) indicates that incorporating the MCC (the first term) into MEE can also generate the fiducial points at zero.To make a balance between the correntropy and error entropy,(20) can be rewritten by

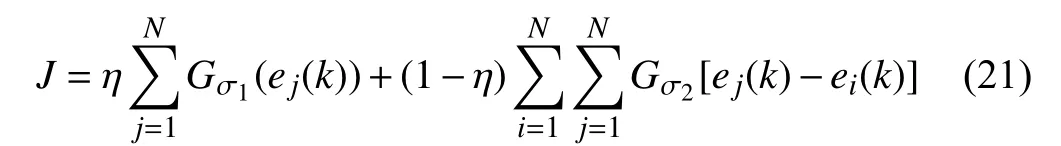
with the scaling factor η ∈[0,1] and kernel sizes σ1and σ2.Based on MEEF,the optimal solution can be obtained when the errors are impelled to move towards zero.The MEEF inherits the nature of the correntropy and error entropy,where the MEE term minimizes the error entropy and the MCC anchors the peak of the error PDF at zero,and the scaling factor indicates the proportion of fiducial points at zero [47].Therefore,MEEF can outperform MCC and MEE.

III.CUBATURE KALMAN FILTER UNDER MINIMUM ERROR ENTROPY WITH FIDUCIAL POINTS

In this section,a novel robust cubature Kalman filter under minimum error entropy with fiducial points is presented by constructing a batch regression model,determining free parameters and robust state estimation,respectively.

A.Regression Model

The batch regression model is required for augmenting the state prediction error together with the measurement.The state estimation is then transformed into performing MEEF over the constructed batch regression model.

Inspired by the nonlinear measurement function (2),a regression model involving measurement equation and state prediction error is constructed by

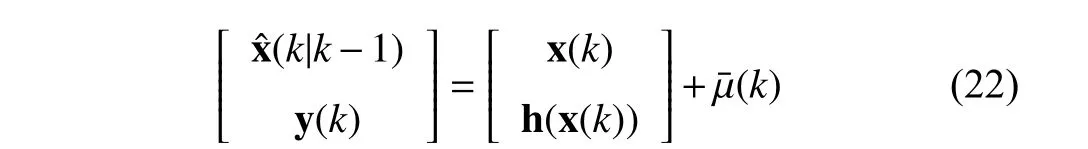
The statistical linearization in [48] is preferable for approximating a nonlinear function accurately.The properties of statistical linearization can be found in [48].Applying the statistical linearization into (2) yields a linearized measurement function

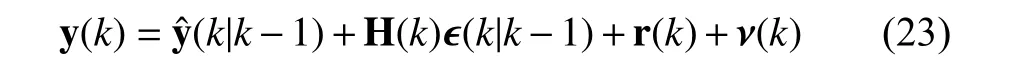
where the linearized matrix H(k) relates to the covariance matrix of the state estimation error Pxx(k|k-1) and crosscovariance matrix Pxy(k|k-1)

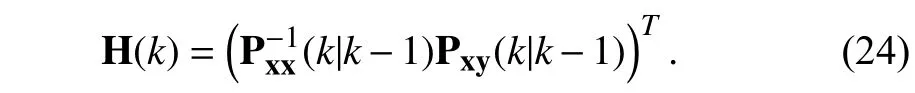
Apart from the linearized matrix H(k),the statistical linearization error ν(k) is a major difference in comparison with traditional linearization approach.The statistical linearization error ν(k) has an essential role in compensating the error caused by linearization and is therefore referred to as compensation factor.

Substituting the linearized measurement function in (23)into (22) yields a novel batch regression model:

whereIndenotes ann×nidentitymatrix and μ(k)=[-ϵT(k|k-1) rT(k)+νT(k)]T.The covariance matrix of μ (k) in (25) is therefore calculated by

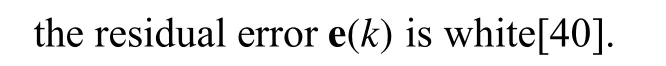
Remark 1:The statistical linearization in [48] is applied for yielding a linearized measurement function shown in (23).The traditional linearization technique may cause large residual errors for nonlinear systems with strong nonlinearity since the nonlinear function is approximated crudely by a lower-order Taylor series expansion.The high-order Taylor series expansion is not recommended since a high-order Jacobian matrix is hard to be calculated.By contrast,the statistical linearization includes a compensation factor or statistical linearization error ν (k) for improving approximation accuracy.Therefore,the statistical linearization can be applied to nonlinear systems with strong nonlinearity in comparison with tradition approaches.

B.Derivation of MEEF-CKF

The MEEF-CKF performs state estimation by performing minimum error entropy with fiducial point over the constructed batch regression model in (27).Substituting (30)into (21),one can obtain the loss function of MEEF-CKF:

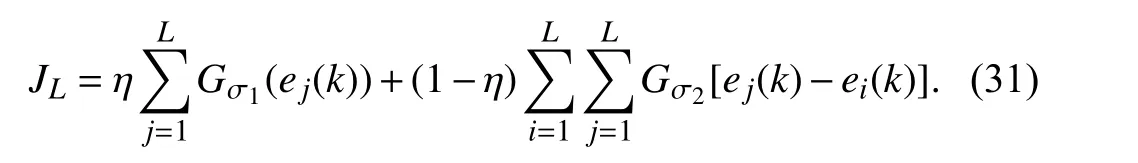
Taking the derivative of theJLwith respect to x (k) yields

Based on the matrix inversion lemma [46],(39) is rewritten as

Note that some extremely large outliers in the measurement may make the matrix Λ(k) singular such that the MEEF-CKF is confronted with numerical issue.We provide the following method to overcome this issue

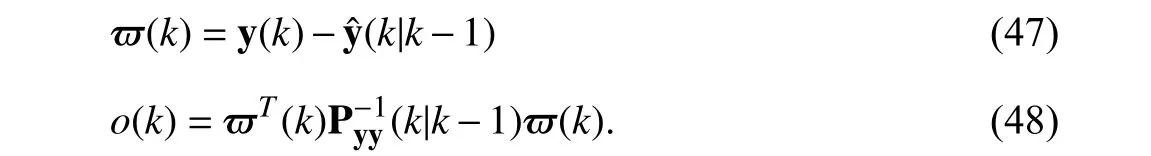
If |o(k)|＞othr,we update the state and covariance matrix by(k)=(k) and P(k)=Pck f(k),whereothris a pre-set threshold,ck f(k) and Pck f(k) are obtained by performing a standard CKF.If |o(k)|＜othr,the MEEF-CKF is performed.With above derivations,the MEEF-CKF is summarized as Algorithm 1.

Step 2: Use (4) and (8) to generate cubature points; use (5) and (6)to obtain(k|k-1) and P(k|k-1),respectively; use (9),(10) and (11)to compute(k|k-1) ,Pyy(k|k-1) and Pxy(k|k-1),respectively; use (24)to obtain the measurement slope matrix H(k); use (47) and (48) to calculate ϖ(k) ando(k),respectively; determine the extreme outliers and handle them; construct the regression model in (27).

Step 3: Use the Cholesky decomposition of Θ(k) to obtain Θp(k|k-1) and Θr(k); use (28) and (29) to obtain d(k) and W(k-1),respectively; substitute (30) into (21).

Remark 2:The thresholdothris essential in detecting extremely large outliers.However,the positive numberothris hard to be chosen sinceothris dependent on varying applications and the magnitude of measurements.An inner quartile range (IQR)-based approach can be used to solve this issue [49].For the sequence,the lower quartile,the second quartile,and the third quartilecan be obtained based on the IQR-based approach [49].When larger than+1.6(-),|o(k)| is regarded as an outlier [49].Therefore,thresholdothris chosen by+1.6(-).

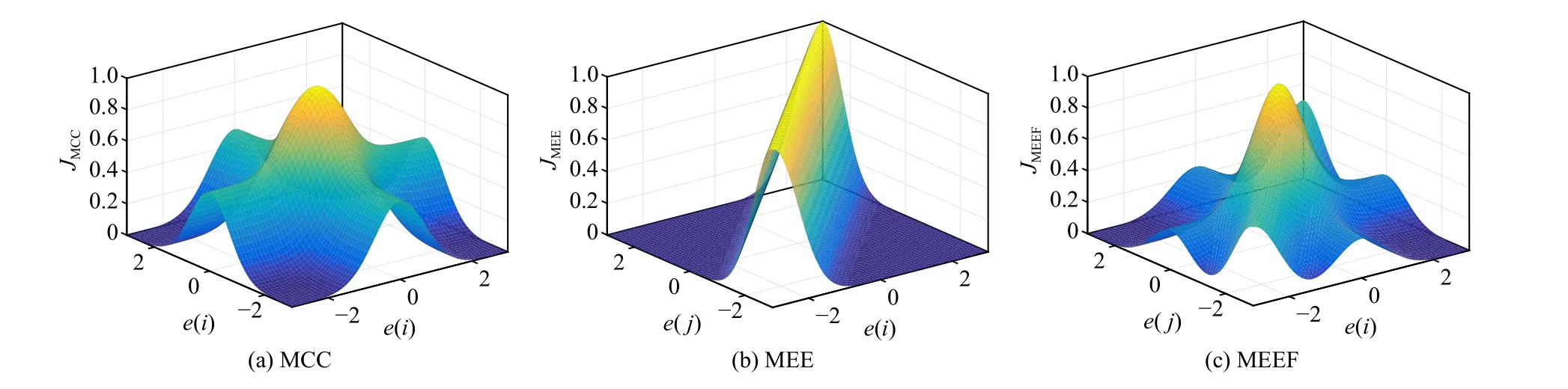
Fig.1.Surfaces of three loss functions in 3D space with N=2: (a) MCC; (b) MEE; (c) MEEF.

Remark 3:Fig.1 gives the surfaces of the loss functions MCC,MEE and MEEF in 3D space.As illustrated in Fig.1,the loss function of MCC not only constrains the location of peak as zero but also influences the shape of loss function for MEEF [47].Thus,all residual errors will identically be close to the peak of loss function,making MEEF-CKF reach an optimal solution [43].

Remark 4:The MEEF-CKF actually retains all merits of the correntropy and error entropy in dealing with multi-modal distribution noises and large outliers.Through the Parzen’s PDF estimator and the Gaussian kernel function,the error entropy behaves strong modeling ability for error distributions especially for multi-modal distributions.Although large outliers may result in abnormale(i) andd(i) in Ξ2,the state posterior estimate(k) in (33) is still robust with the help of correntropy and error entropy.In correntropy,the Gaussian kernel functionGσ1(ej(k))is used to suppress outliers.Similarly,error entropy also exhibits strong robustness through the Gaussian kernel functionGσ2[ej(k)-ei(k)],which degrades the effects of outliers ind(i)or/andd(j).

C.Optimization of the Free Parameters in MEEF-CKF

The estimation accuracy of MEEF-CKF is greatly affected by parametersη,σ1and σ2.For example,the parameterηis utilized for balancing correntropy and error entropy.More concretely,the correntropy or error entropy is switched off by setting η=0 or η=1.In addition,the MEEF-CKF will reduce to the traditional CKF by setting η =1 and σ1→∞.

In this section,an effective optimization method is proposed for determining these parameters.In MEEF,the information potential (IP) with a fiducial point can be divided into three terms:

whereVc=[Gσ1(e)]is the correntropy,Ve=E[p(e)]isthe quadratic Renyi’s in for mation potential,andU(η,σ1,σ2)takes the form:

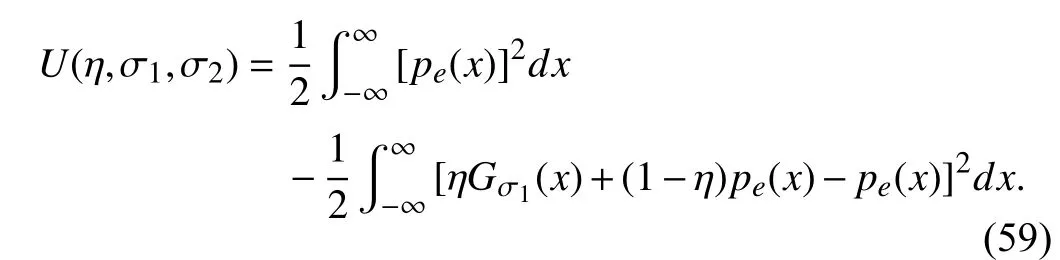
Since the first term in (58) is independent of the error model for givenη,σ1and σ2,the maximization of (58) can be regarded as maximizing (59) [50],[51].For given a model,we can solve the parameters by maximizing

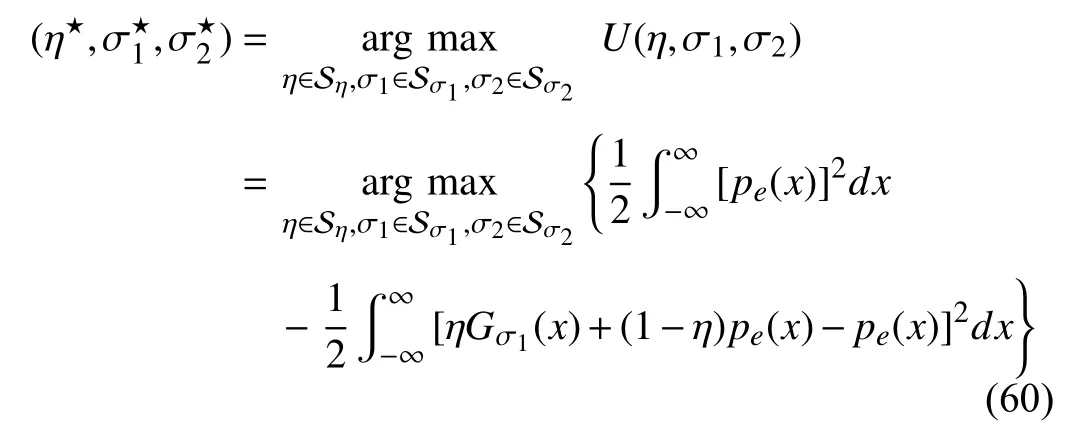
whereSη,Sσ1andSσ2denote the adm issible sets of parametersη,σ1andσ2.When thePDF of errors is fixed at discrete timek,the optimal parameters are determined by

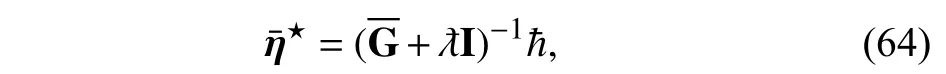
Remark 5:Generally,one can search the optimal parameters from the given finite sets via cross-validation [26].To reduce the computational complexity,the free parameters are jointly optimized by minimizing the function (65).Kernel sizesσ1andσ2canbeoptimized alternately on finite sets Sσ1and Sσ2.Specifically,given predesignedSσ1andSσ2,onecan optimize each kernel size one by one,and repeat the process S times.Theoretically,a much more smaller or larger kernel parameter is not beneficial for Kalman filters performing dynamic estimation.For example,a greatly small kernel size may cause numerical stability problems (See convergence analysis in Section IV).In contrast,a much more larger kernel size weakens the robustness of MEEF-CKF because outliers are not be detected.The specific guidelines for range of kernel size can be found in reference [26],which provides the reference to determine Sσ1and Sσ2.

IV.PERFORMANCE ANALYSIS

A.Computational Complexity Analysis

Table I analyzes the computational complexity of MEEFCKF at each step of Algorithm 1.Notationsnandmrepresent the dimensions of the state x(k) and measurement y(k),respectively.The overall cost is calculated by considering the highest order of magnitude withm＜n.CfandChdenote the computational complexity of evaluation of f and h on sample points ξi(k-1) and ξi(k|k-1),respectively.Cesymbolizes the calculational burden of an exponential function on a scalar.From Table I,the estimated computational complexity of every variable in MEEF-CKF does not exceedO(4n3).As a result,the computational cost of MEEF-CKF is three order of magnitude per iteration.These results are the same as the traditional CKF.

where scalar τ is an average fixed-point iteration number which is in general small [40].Since the scale of measurements is in general far smaller than that of the state,i.e.,m＜＜n,(66) in fact can be further simplified as

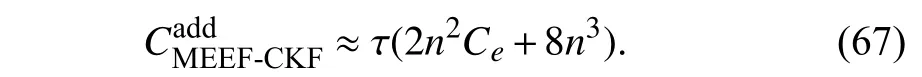
The proposed MEEF-CKF therefore generates extra τ(2n2Ce+8n3)computational burden in comparison with the CKF.

B.Convergence Issues

A sufficient convergence condition about the fixed-point iteration update is provided in this section where the proofs is based on [39],[45].For simplification,we assume that kernel sizes satisfy σ1=cσ2with nonnegative constantc.

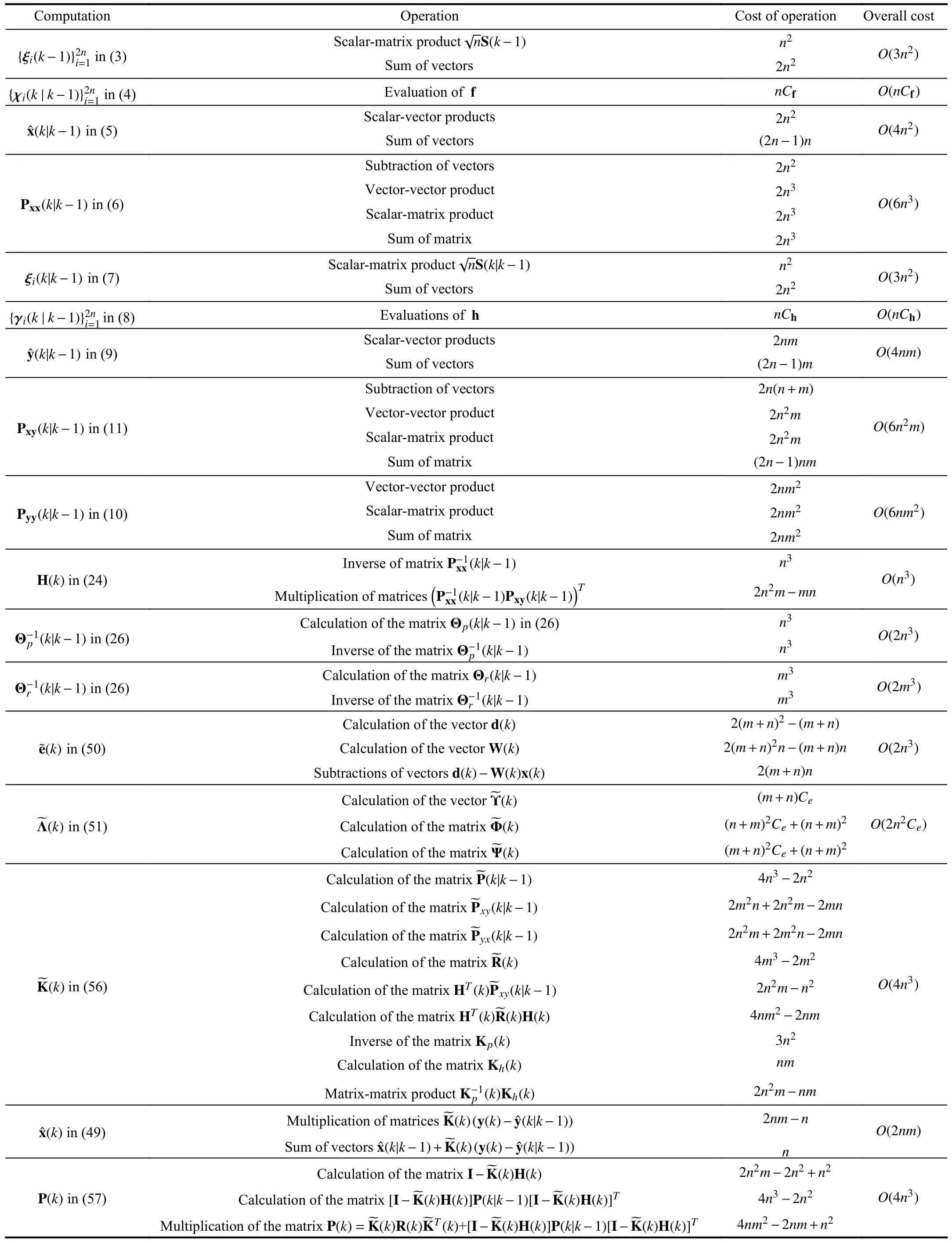
TABLE ICOMPUTATIONAL COMPLEXITY OF CUBATURE KALMAN FILTER UNDER MINIMUM ERROR ENTROPY WITH FIDUCIAL POINTS

Therefore,the following T heorem 1 holds.

Theorem 1:If the kernel size satisfiesσ2≥max{σ†1,σ†2}and

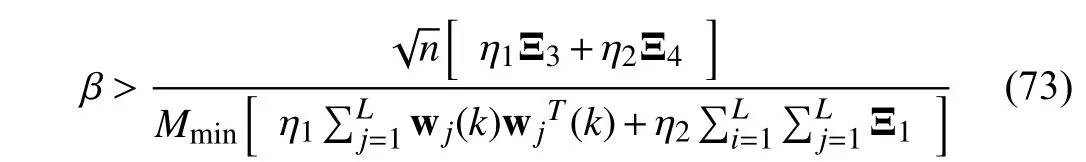
where σ†1and σ†2are the solutions of φ1(σ2) and φ2(σ2),we have

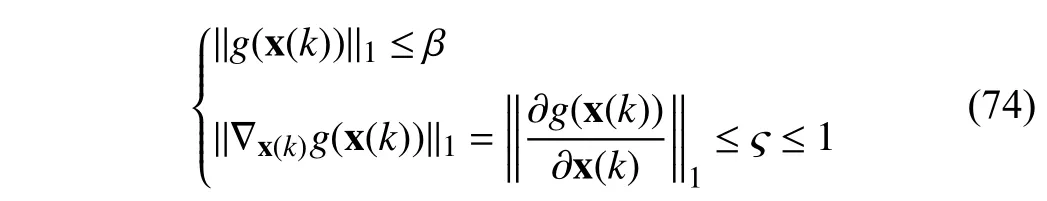
where ς=φ2(σ2).The proof of Theorem 1 is omitted because it is an extension of the proofs in [39] and [45].

According to [39],[45],if σ2≥max{σ†1,σ†2} and||x(k)0||1≤β,x(k) converges to a unique fixed-point in the range x (k)∈{||x(k)||1≤β} can be ensured.

V.ESTIMATION RESULTS

The filtering performance of the proposed algorithm is tested by target tracking with INS/GPS integrated system,and Fig.2 shows the trajectory of aircraft.Define the INS body frame (Right-Forth-Up) byb-frame,the navigation frame(East-North-Up,ENU) byt-frame,the computed reference navigation frame byt′-frame,the earth-centered,earth-fixed(ECEF) bye-frame (WGS84),the geocentric inertial coordinate frame byi-frame (J2000) [22].Denote the target

Fig.2.True trajectory of aircraft.

where x(k)=[φT,ΔvT,ΔpT,δζT,δaT]Tand the function f(·) is obtained by (75).The process noise covariance matrix takes the form of Q(k)=diag(01×9,Qg,Qa) withQg=[Qge,Qgn,Qgu] and Qa=[Qae,Qan,Qau].Subtracting the position of GPS from INS,we have the measurement equation:

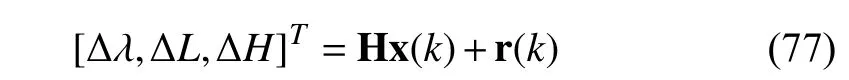
whereΔλ=λINS-λGPS,ΔL=LINS-LGPS,ΔH=HINSHGPS;H=[03×6,I3×3,03×6]; r(k)=[r1(k),r2(k),r3(k)]Tdenotes the measurement noise.Here,the frequencies of INS and GPS are 10 Hz and 1 00 Hz,respectively.The random errors in gyro and accelerometer are 0.03°/h and 100 μg m/s2.The gyro and accelerometer error drift correlation time are τg=300 s and τa=1000 s,respectively.The positioning error of the GPS system is 1 0 m-100 m.

The robustness of MEEF-CKF is compared with that of nonlinear Kalman filters including the EKF,UKF,CKF,MCCKF [42],minimum error entropy extended Kalman filter(MEE-EKF) [46],stochastic integration student’s t filter(SISTF) [29],robust student’s t based stochastic cubature filter (RSTSCF) [30].In addition,key parameters includingη,σ1and σ2are vital for improving filtering accuracy.Therefore,different methods for choosing parameters of MEEF-CKF are considered.The MEEF-CKF (trial) represents that MEEF-CKF performs target tracking with free parameters chosen by numerous trials.This approach is a hard manner for finding unknown parameters where parameters are predesigned and not adaptive.A soft manner,i.e.,MEEF-CKF(optimization) is therefore presented for avoiding this issue.In MEEF-CKF (optimization),those free parameters are adaptively updated as shown in Algorithm 2.

Several performance metrics including root mean square error (RMSE) [30],[52] and root time averaged MSE(RTAMSE) [30],[52] are utilized for evaluating the filtering precision in complex non-Gaussian noises.Note that position variablesλ(latitude) andL(longitude) have units degree (°) in Kalman filtering.The unit is converted into meter (m) in calculating the corresponding RMSE and RTAMSE.Rewrite the position p=[λ,L,H]Tas p=[p1,p2,p3]Twith the unit meter (m).The RMSE of position at discrete timekover Monte Carlo runs is defined by

whereNdenotes the number of samples.Similarly to the RMSE and RTAMSE of position,we can also define the RMSE and RTAMSE of velocity.In all simulations,results are averaged over 300 independent runs.In order to make a fair comparison,all nonlinear Kalman filters are run under similar initial conditions.In particular,observable state,i.e.,xo(k) is initialized by measurements for all nonlinear Kalman filters.As for the hidden state xu(k),all nonlinear Kalman filters are initialized by zero value.The initial covariance matrix of estimated error P(0) is set as an identity matrix.The process noise is a zero mean Gaussian distribution with the covariance matrix Q(k) determined from the stochastic error of inertial sensors,and set asQ(k)=diag[01×9,(0.03°/h)2,(0.03°/h)2,(0.03°/h)2,(100 μg m/s2)2,(100 μg m/s2)2,(100 μg m/s2)2].Notation h denotes 1 h,andg=9.78 m/s2represents the gravitational acceleration.The measurement noise matrix R(k) is determined by the GPS’s stochastic measurement error.In this section,different measurement noises including three types of synthetic noises and one realworld noise are considered.

A.Gaussian Noise With Outliers

In this scenario,measurement noises are modelled by Gaussian noise with outliers and described by

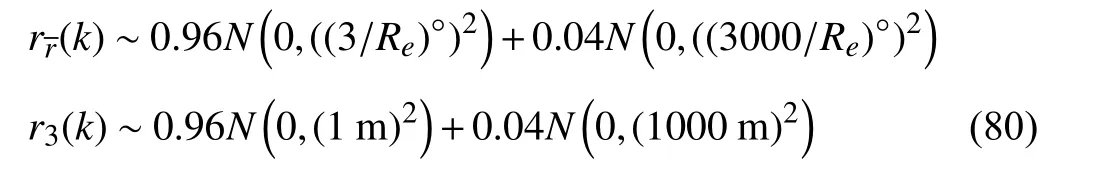
Apart from the RTAMSE shown in Fig.3 and Table II,RMSEs of position and velocity for all nonlinear Kalman filters are studied in Fig.4.From Fig.4,the MCCKF,MEEEKF,SISTF,RSTSCF and MEEF-CKF all have improved robustness in comparison with the EKF,UKF and CKF.In addition,the proposed MEEF-CKF (optimization) and MEEFCKF (trial) behave enhanced robustness against non-Gaussian noises in comparison with other Kalman filters.It is also necessary to note that the MEEF-CKF (optimization) has slightly higher estimation precision than the MEEF-CKF(trial).

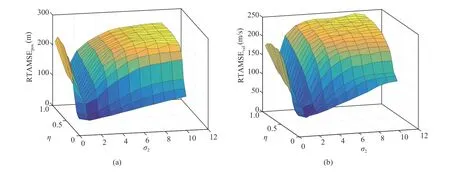
Fig.3.RTAMSEs of MEEF-CKF versus σ 2 and η under Gaussian noise with large outliers: (a) Position; (b) Velocity.

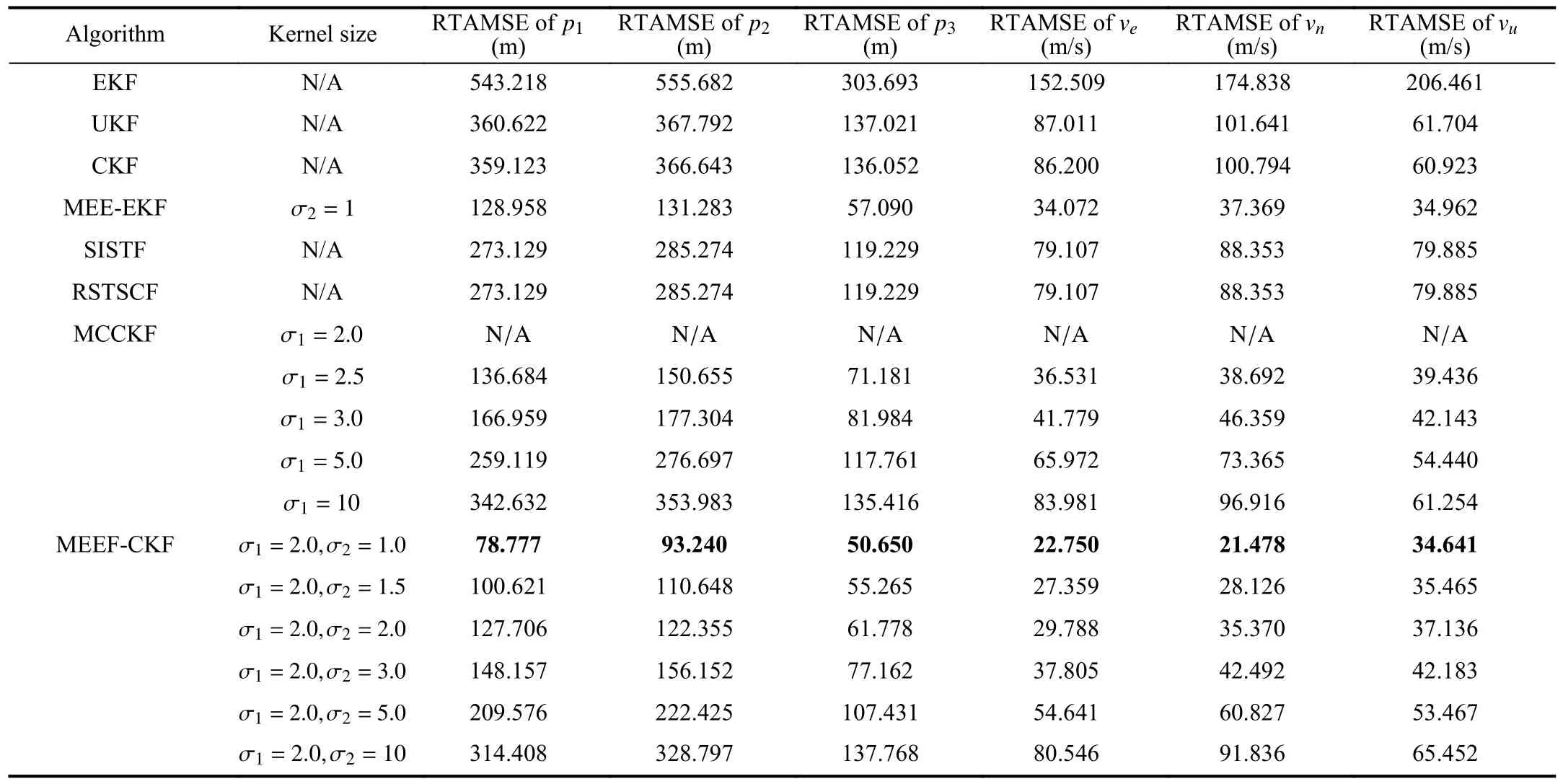
TABLE IIRTAMSES OF DIFFERENT ALGORITHMS UNDER GAUSSIAN NOISE WITH LARGE OUTLIERS

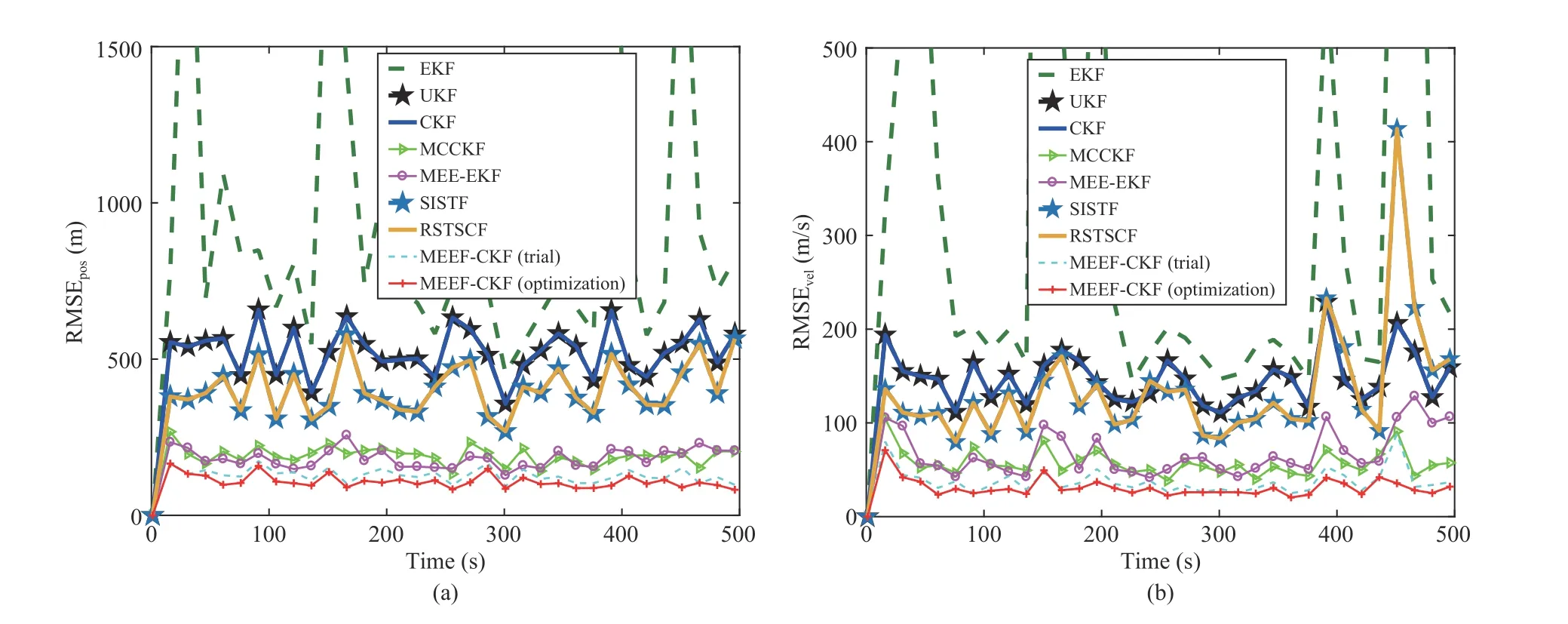
Fig.4.RMSEs of different algorithms under Gaussian noise with outliers: (a) Position; (b) Velocity.

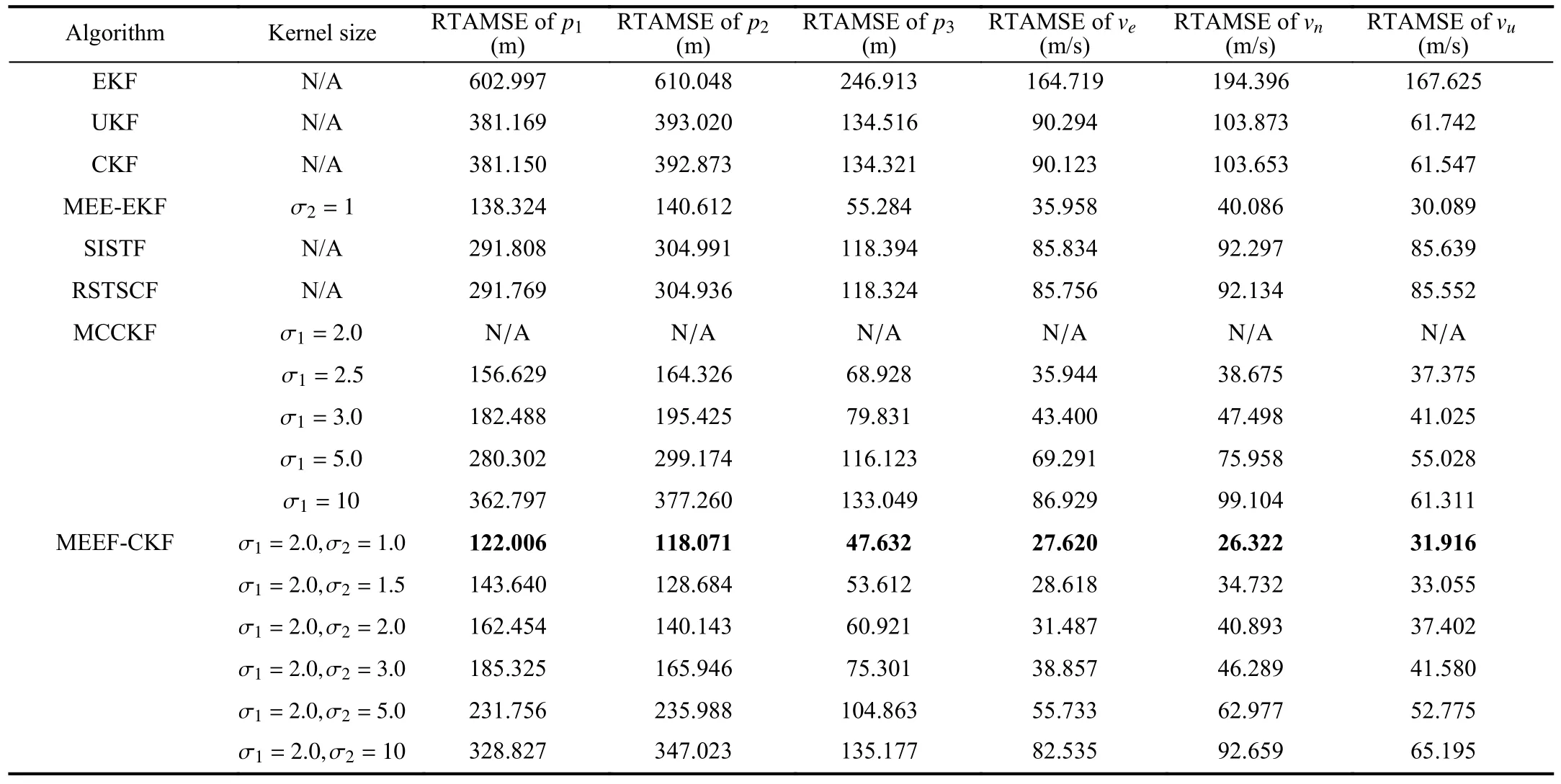
TABLE IIIRTAMSES OF DIFFERENT ALGORITHMS UNDER BIMODAL GAUSSIAN MIXTURE NOISES

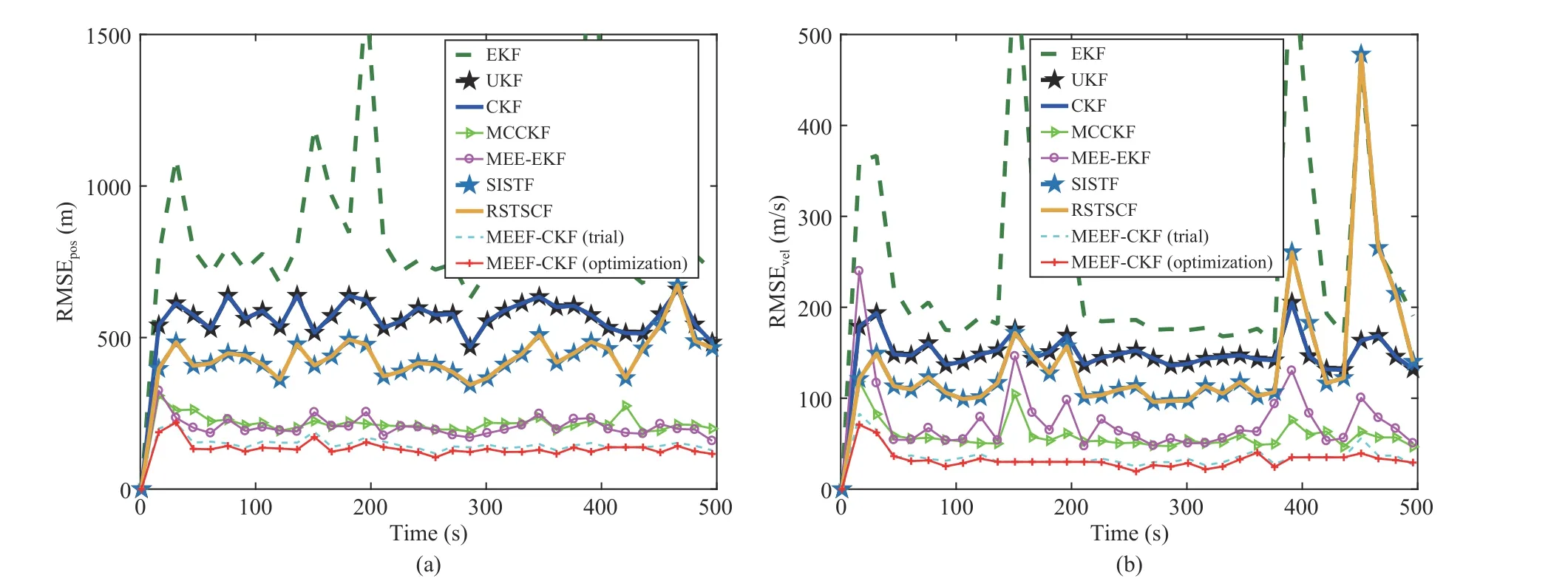
Fig.5.RMSEs of different algorithms under bimodal Gaussian mixture noises: (a) Position; (b) Velocity.

B.Bimodal Gaussian Mixture Noises

Apart from above Gaussian distribution with outliers,the bimodal Gaussian mixture noises are further considered here which are described by

The DoF parameters of SISTF and RSTSCF and scaling factor of MEEF-EKF (trial) are the same as those in Case A.Table III shows RTAMSEs of different algorithms under bimodal Gaussian mixture noises.From Table III,the filtering accuracy of the MCCKF is degraded greatly by much smaller kernel size.By contrast,the MEEF-CKF always achieves the best estimate performance among all Kalman filters under the appropriate choice of kernel sizes and scaling factor.Fig.5 presents the RMSEs of position and velocity for different Kalman filters.From Fig.5,the MEEF-CKF behaves superior filtering performance in comparison with other Kalman filters.In addition,the MEEF-CKF (optimization) performs better than the MEEF-CKF (trial) in dealing with non-Gaussian noises.

C.Bimodal Gaussian Mixture Noises With Outliers

At this scenario,we consider the bimodal Gaussian mixturenoises with outliers which are modelled by combing the Gaussian noise with outliers and bimodal Gaussian mixture noises.

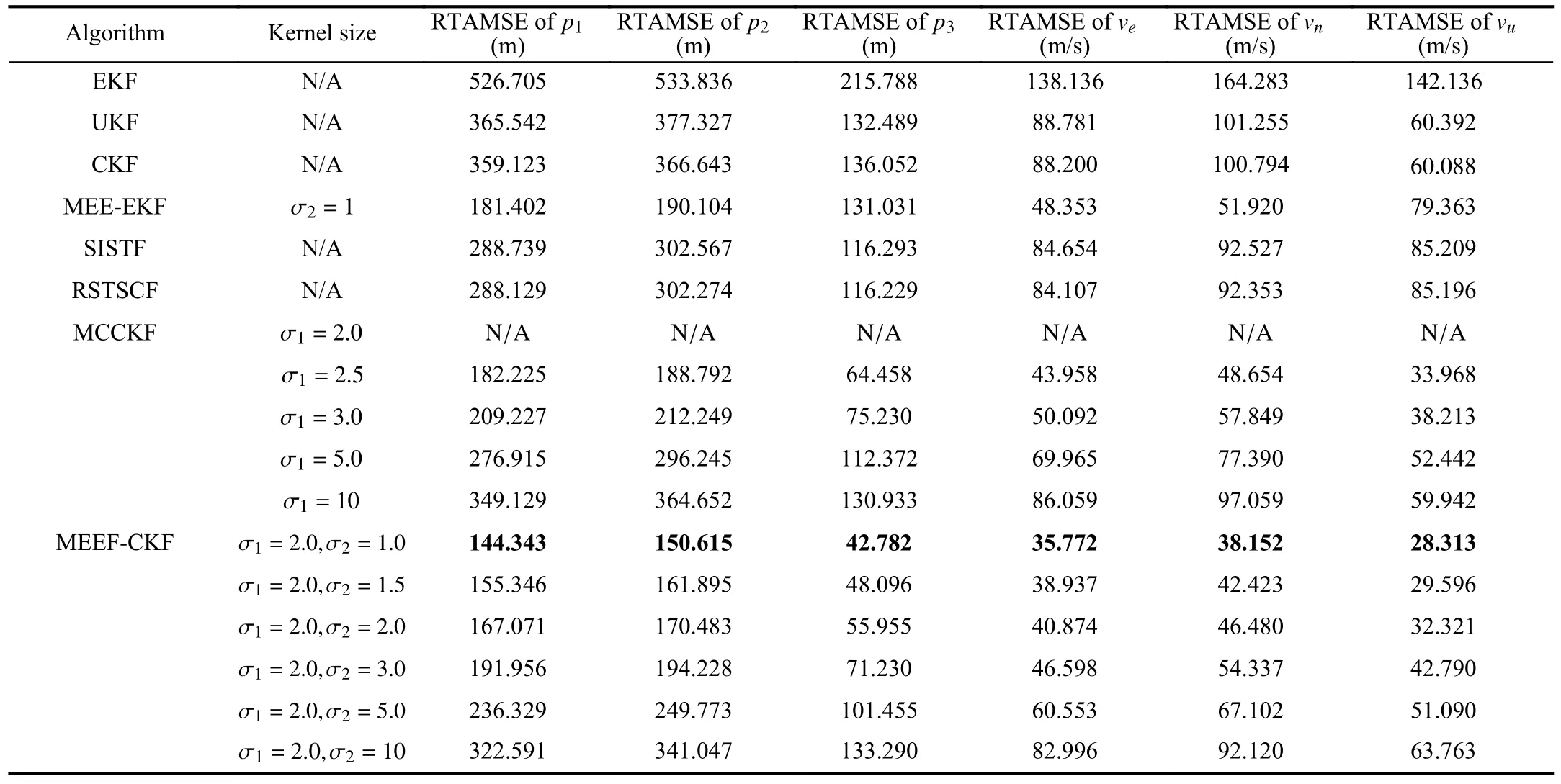
TABLE IVRTAMSES OF DIFFERENT ALGORITHMS UNDER BIMODAL GAUSSIAN MIXTURE NOISES WITH OUTLIERS

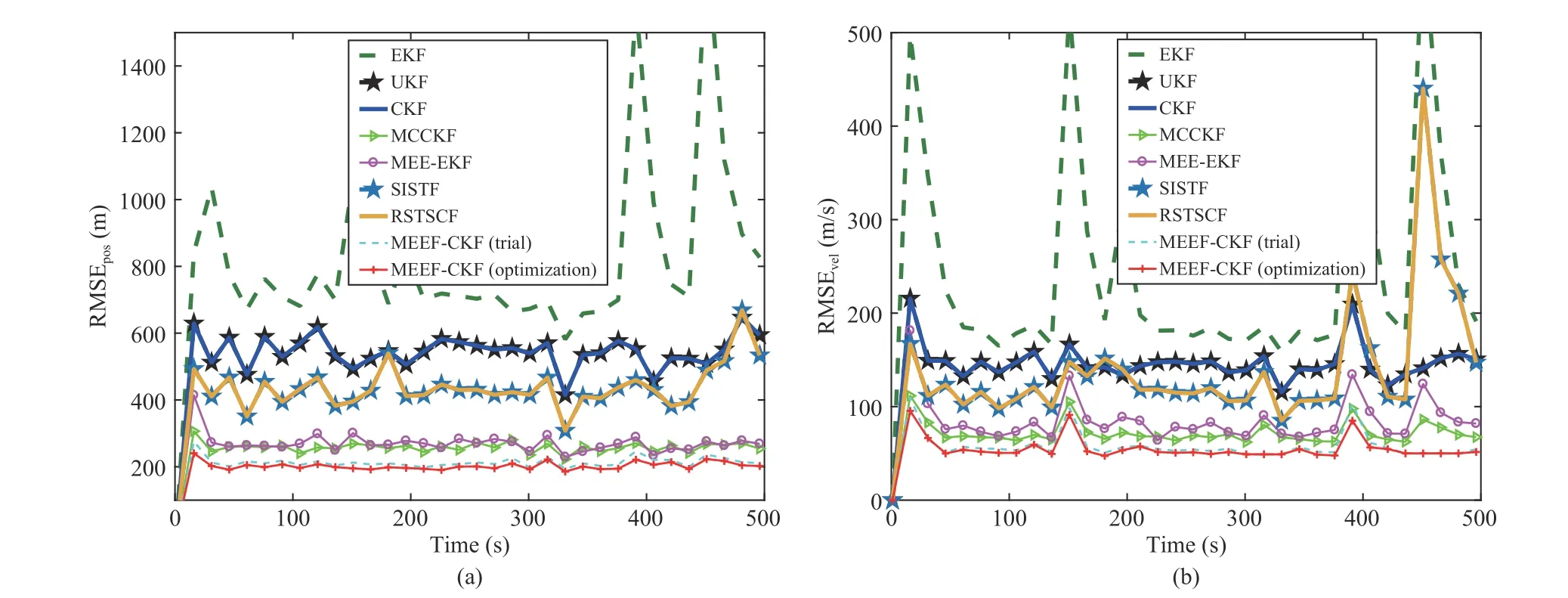
Fig.6.RMSEs of different algorithms under bimodal Gaussian mixture noises with outliers: (a) Position; (b) Velocity.

The DoF parameters of SISTF and RSTSCF and scaling factor of the MEEF-EKF (trial) are the same as those in Case A.Table IV shows RTAMSEs of different Kalman filters under bimodal Gaussian mixture noises with outliers.Fig.6 presents the RMSEs of position and velocity for different algorithms.From Table IV and Fig.6,the same conclusions as those in case B are obtained.

D.Real-World Noise

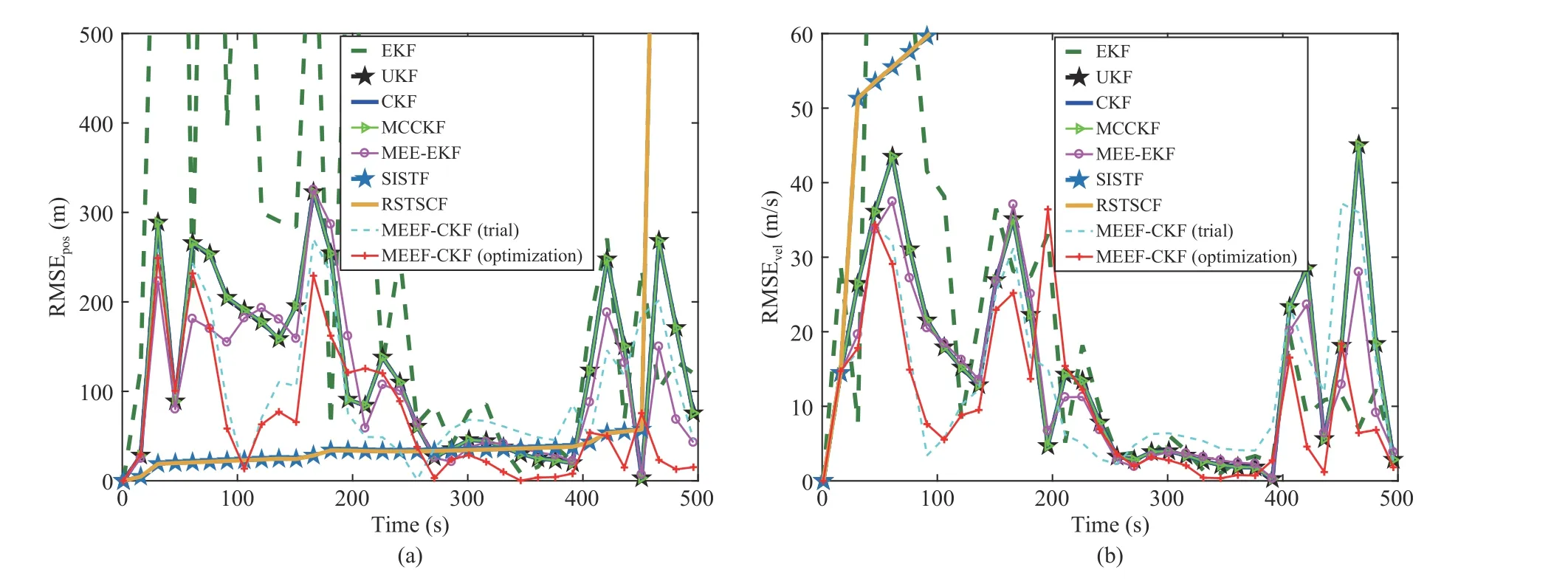
Fig.7.RMSEs of different algorithms under real-world noise: (a) Position; (b) Velocity.

The measurement noise in real-world is in fact much more complex than noises in Sections V-A,V-B and V-C.Apart from different noises studied in Sections V-A,V-B and V-C,the filtering robustness of MEEF-CKF is therefore further demonstrated in real-world noises.At this scenario,the process noise covariance matrix Q (k) is set by using the errors of the gyro and accelerometer.The measurement noise covariancematrixR(k)=diag((1.52×10-2)°,(1.60×10-2)°,6.90×101m)2isset by using theGPS’s stochastic measurement error.The DoF parameters in SISTF and RSTSCF are all set as 0.005,and the scaling factor in MEEFEKF (trial) is 0.85.Fig.7 presents the RMSEs of the position and velocity for different algorithms.From Fig.7,we observe that the SISTF and RSTSCF achieve higher filtering accuracy than other filters in terms of position estimation in the early stage but diverge at the late stage.Similar conclusion can also be obtained for velocity estimation.As for the MEEF-CKF,the filtering performance of MEEF-CKF is superior to that of other algorithms in complicated noises.Although the MEEFCKF performs worse than other filters at small noises,all Kalman filters achieve desirable filtering precision.In addition,the MEEF-CKF (optimization) in general behaves better than the MEEF-CKF (trial).From aspect of computational complexity,the average computing time of the UKF,CKF,MCCKF,MEEF-CKF(trial)andMEEF-CKF(optimization)is2.40×10-4s,1.120×10-4s,3.39×10-4s,6.62×10-4s and 7.12×10-4s,respectively.As the MEEFCKF needs to calculate more matrices in (66),the MEEF-CKF requires more but completely acceptable computing time.It is also necessary to note that the computing time of all filters has no significant difference in terms of order of magnitude.

VI.CONCLUSIONS

In this paper,a novel robust nonlinear Kalman filter called cubature Kalman filter under minimum error entropy with fiducial points (MEEF-CKF) is proposed for handling large outliers and multimodal distribution noises.The MEEF-CKF inherits the merits of the minimum error entropy (MEE) and maximum correntropy criterion (MCC),and therefore outperforms the MEE-based and MCC-based Kalman filters.In addition,the free parameters in MEEF-CKF are jointly optimized by minimizing the objective function.The computational complexity and convergence analyses of the MEEF-CKF are provided for demonstrating calculational burden and stability.The improved robustness of MEEF-CKF and effectiveness of parameter optimization have been demonstrated in the application of target tracking with INS/GPS integration disturbed by non-Gaussian noises.

APPENDIX

From (23),we obtain