锈蚀钢筋混凝土柱等效塑性铰长度计算方法
郑跃,郑山锁,董立国,张艺欣,杨松
(1.西安建筑科技大学土木工程学院,陕西西安,710055;2.西安建筑科技大学结构工程与抗震教育部重点实验室,陕西西安,710055)
随着服役龄期增长,钢筋混凝土(concrete column,RC)结构暴露出耐久性问题,其中钢筋锈蚀造成的RC结构损伤最严重,在实际工程中也最常见[1]。RC 柱作为结构的主要竖向承重和抗侧力构件,确定其塑性转动能力和极限位移是研究结构整体性能和抗倒塌性能的关键。在强烈地震作用下,RC柱两端易进入塑性状态,为此,国外学者引入“等效塑性铰”概念,通过确定等效塑性铰长度Lp及相应的塑性铰转动能力,简化计算RC柱的塑形转角和极限位移。然而,RC柱中钢筋锈蚀会造成纵向受力钢筋的有效截面面积减小和力学性能降低,减小箍筋对核心区混凝土的约束作用[2],进而影响其承载力和变形能力。因此,有必要研究锈蚀RC柱的等效塑性铰长度和相应的塑性铰转动能力,确定其塑形转角和极限位移。
假定等效塑性铰长度范围内的塑性曲率为常数,通过等效塑性铰长度Lp、柱高、柱底截面屈服曲率以及极限曲率可计算柱底塑性铰转动能力和柱顶极限位移,因此,Lp取值合理性直接决定了等效塑性铰模型的准确性。目前,国内外学者大量研究了RC 柱的等效塑性铰长度计算方法。PRIESTLEY 等[3]基于钢筋混凝土桥墩柱的拟静力试验结果和理论分析,建立了包含柱高和纵筋直径等参数的等效塑性铰长度计算公式。PAULAY等[4]研究了纵筋强度等级对等效塑性铰长度的影响,并结合试验结果修正了PRIESTLEY 等[3]建立的等效塑性铰长度计算公式。孙治国等[5]在大量钢筋混凝土墩柱试验基础上,对比了各国主要等效塑性铰长度计算公式,讨论了影响墩柱等效塑性铰长度的主要因素,并通过回归分析建立了等效塑性铰长度计算公式。李贵乾等[6]建立了圆形桥墩极限位移三分量模型,研究了弯曲、剪切和纵筋滑移变形对桥墩塑性转角及柱顶位移的影响,并基于试验数据建立了桥墩等效塑性铰长度理论及经验计算公式。上述研究虽已建立了大量RC柱等效塑性铰长度计算公式,得出影响等效塑性铰长度的因素主要有柱高、纵筋直径、屈服强度、混凝土抗压强度、截面宽度和塑性铰区箍筋约束等,但需要指出的是,目前研究均未考虑钢筋锈蚀对等效塑性铰长度及转动能力的影响。
鉴于此,本文基于前期试验结果,首先深入分析地震作用下锈蚀RC 柱的破坏机理及变形特点,并考虑锈蚀对钢筋、混凝土以及钢筋与混凝土间黏结性能的影响,建立了包含弯曲效应和应变渗透效应的锈蚀RC 柱等效塑性铰长度计算模型;其次,通过理论分析与推导,标定了模型参数,最终建立了考虑锈蚀率、配筋率、柱高和材料特性参数的锈蚀RC 柱等效塑性铰长度计算公式;最终,与试验结果进行对比,验证其准确性。
1 破坏过程分析
为研究锈蚀RC 柱等效塑性铰长度计算方法,首先需要充分了解其锈蚀损伤形态和破坏机理。本文根据课题组前期所进行的锈蚀RC柱拟静力试验[7],深入分析氯盐侵蚀作用下锈蚀RC 柱的破坏过程。
1.1 锈蚀形态
RC 柱典型锈蚀损伤形态如图1所示。由图1可见:试件红褐色锈蚀产物透过混凝土保护层微细孔渗出,并部分黏附在试件表面;试件表面出现明显锈胀裂缝,且多集中于试件角部并沿纵筋方向分布。根据RC柱锈蚀损伤形态可知,混凝土保护层锈胀开裂将致使其强度降低,纵筋锈蚀将导致其截面面积减小以及屈服强度降低,纵筋锈蚀产物将劣化其与混凝土间黏结性能,箍筋锈蚀导致其对核心区混凝土的约束程度降低,因此,在建立锈蚀RC柱等效塑性铰长度计算模型时应充分考虑上述因素的影响。

图1 试件表面锈胀裂缝形态[7]Fig.1 Corrosion crack distributions on corroded specimens surface[7]
1.2 加载破坏过程
锈蚀RC 柱典型破坏形态如图2所示。试件破坏时在柱底形成塑性区,并伴随明显塑性变形,整个加载过程可以分为3个阶段。

图2 试件破坏形态Fig.2 Failure patterns of specimens
1)加载初期,柱底混凝土首先出现水平裂缝,数量不断增加、宽度不断加宽。此时截面整体刚度基本不变,试件尚处于弹性阶段,柱底无塑性区形成。
2)随着荷载或位移增加,水平裂缝逐渐向内延伸,由于锈胀裂缝的存在,受压侧保护层混凝土较早脱落,随后受拉纵筋屈服;纵筋屈服后其应变急剧增加,导致柱底部产生塑性弯曲变形,并且由于基底锚固区内混凝土与纵筋变形不协调,会在一定长度内发生纵筋应变渗透效应,使柱身产生滑移塑性变形,这一阶段柱底部开始出现塑性铰区。
3)伴随着荷载或位移进一步增加,柱底受压侧混凝土出现竖向裂缝,受压区混凝土破碎面积逐渐增大,塑性区高度不断向上扩展。由于锈蚀导致箍筋截面积减小,部分试件最终破坏时箍筋断裂。在整个加载过程中几乎未出现剪切斜裂缝,各试件均呈现典型弯曲破坏特征。
通过锈蚀RC柱加载破坏过程可知,钢筋锈蚀将导致纵筋及箍筋截面积减小,箍筋对核心区混凝土约束程度降低,纵筋与混凝土间黏结性能劣化等。张勤等[8−9]的研究表明,纵筋应变渗透效应对锈蚀RC柱顶位移贡献较大,并且对于弯曲及弯剪型破坏RC柱,其破坏时柱底剪切斜裂缝开展并不充分,剪切变形占整体变形比例极小,可以忽略。因此,在建立锈蚀RC柱塑性铰长度计算模型时需包含弯曲变形和纵筋滑移变形,并考虑钢筋锈蚀对混凝土、钢筋力学性能及混凝土与钢筋间黏结性能的影响。
2 等效塑性铰长度定义
PRIESTLEY 等[3]提出了等效塑性铰长度的概念,如图3所示。将图3中实际曲率分布简化为沿柱高L线性分布的屈服曲率φy和在塑性铰长度Lp范围内均匀分布的塑性曲率φp,并假定柱顶塑性转动集中于等效塑性铰区内。
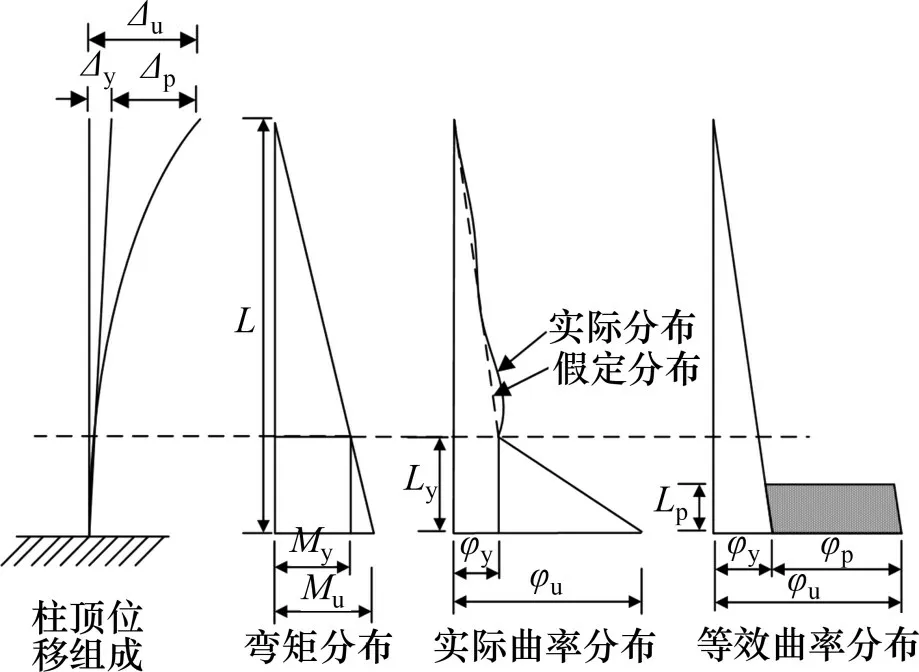
图3 等效塑性铰长度定义Fig.3 Definition of equivalent plastic hinge length
简化曲率沿柱高的分布,运用曲率积分原理可得到柱顶极限位移计算公式:

式中:Δy,Δp和Δu分别为柱顶屈服位移、塑性位移和极限位移;φy,φp和φu分别为屈服曲率、塑性曲率和极限曲率;L为柱高;Lp为等效塑性铰长度。
由等效塑性铰长度定义可知,通过平均塑性曲率与等效塑性铰长度乘积可获得RC柱底塑形转角,并进一步计算得到柱顶极限位移。平均塑性曲率可通过截面P−M−φ分析确定,但对P−M−φ分析一般仅能得到截面弯曲曲率,而不能考虑柱底纵筋滑移效应。本文基于P−M−φ获得柱底塑性曲率,计算柱顶极限位移时需在等效塑性铰长度Lp中考虑柱底纵筋滑移效应。
3 计算模型
3.1 考虑钢筋锈蚀影响的塑性曲率
根据梁兴文等[10]的研究,取RC 柱截面受拉区纵向钢筋应变达到屈服应变εy时的曲率作为截面的屈服曲率φy,取受压区边缘约束混凝土应变达到极限应变εccu时的曲率作为截面的极限曲率φu。结合平截面假定与钢筋、混凝土本构关系,采用截面P−M−φ分析,求解RC柱截面各特征点曲率φ。
考虑钢筋锈蚀损伤影响,定义保护层以及核心区混凝土的本构关系,如图4所示。

图4 混凝土本构关系Fig.4 Constitutive relation of concrete
1)保护层混凝土。保护层混凝土本构关系采用KENT-SCOTT-PARK 模型[11],并参考文献[12−13],考虑保护层混凝土锈胀开裂的影响,确定保护层混凝土峰值应力f′cC,计算公式如下:
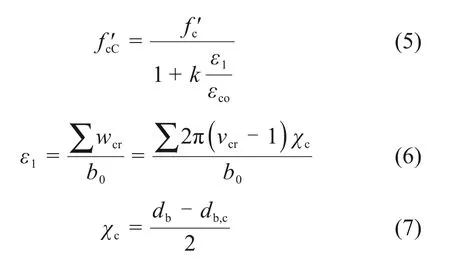
式中:k为与钢筋直径和表面粗糙度有关的系数,按文献[12],k=0.1;b0为柱截面周长;wcr为锈胀裂缝宽度;νcr为锈蚀钢筋的体积膨胀比,MOLINA等[13]建议取2;χc为锈蚀深度;db,c为锈蚀钢筋直径。
2)核心区混凝土。核心区混凝土本构关系采用MANDER 模型[14],考虑箍筋锈蚀对核心区混凝土约束作用的降低,参考文献[15],确定锈蚀箍筋约束混凝土本构模型参数,计算公式如下:
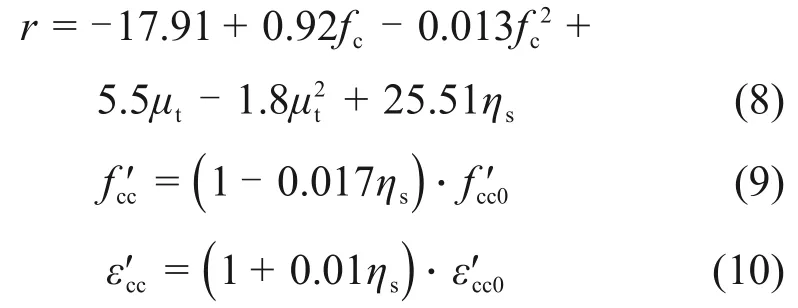
式中:r为形状系数;fc为混凝土强度;μt为配箍率;ηs为箍筋锈蚀率;f′cc0和ε′cc0分别为约束混凝土的峰值应力和峰值应变。
3.2 弯曲塑性变形
RC 柱底的弯曲塑形转角可通过塑性曲率沿塑性区积分确定,在侧向力作用下,柱底进入塑性状态时的截面弯矩及曲率沿柱高分布如图5所示。
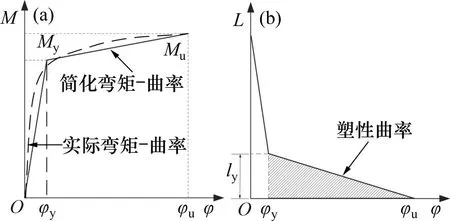
图5 弯矩及曲率沿柱高分布Fig.5 Bending moment and curvature distributions
当柱底截面弯矩大于屈服弯矩My后,认为截面进入塑性阶段,开始出现“塑性铰”,因此,柱底塑性区长度ly为
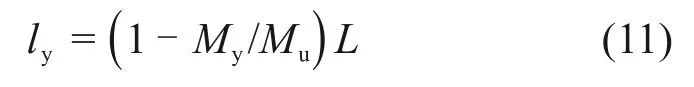
相应的弯曲塑性转角θflex为

式中:L为柱高;ly为柱底塑性区长度;My和Mu为分别为柱截面屈服弯矩与极限弯矩。
3.3 纵筋滑移变形
3.3.1 锈蚀钢筋混凝土黏结滑移模型
随着侧向力增加,柱底纵筋应力和应变不断增大,当钢筋应力达到纵筋与混凝土的黏结强度时,纵筋与柱底锚固区混凝土将产生相对滑移,引起柱底区域附加转动θslip(见式(13))以及柱顶滑移变形,如图6所示。
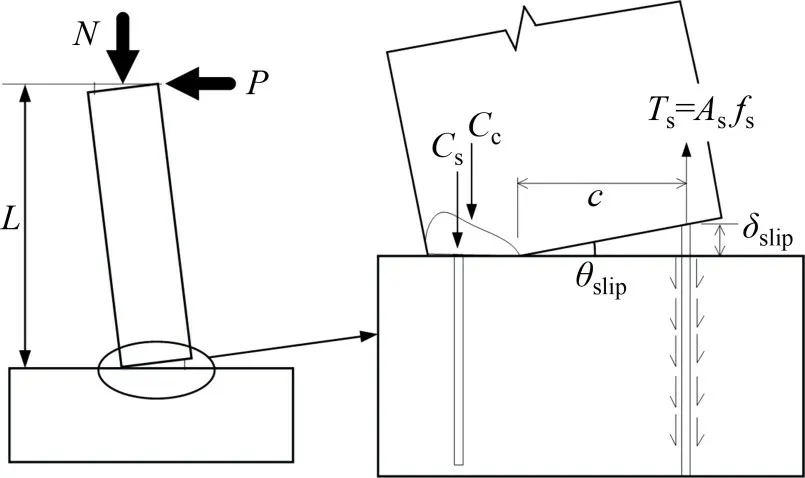
图6 纵筋滑移变形Fig.6 Deformation due to longitudinal bar slip

式中:δslip为柱底纵筋与混凝土相对滑移;c为柱底截面受拉区高度。
钢筋锈蚀将劣化钢筋与混凝土间黏结性能,本文在两段式黏结应力分布简化模型[16]基础上,参考文献[17],建立锈蚀钢筋混凝土黏结滑移模型,计算柱底钢筋与混凝土间相对滑移δslip,模型示意如图7所示。
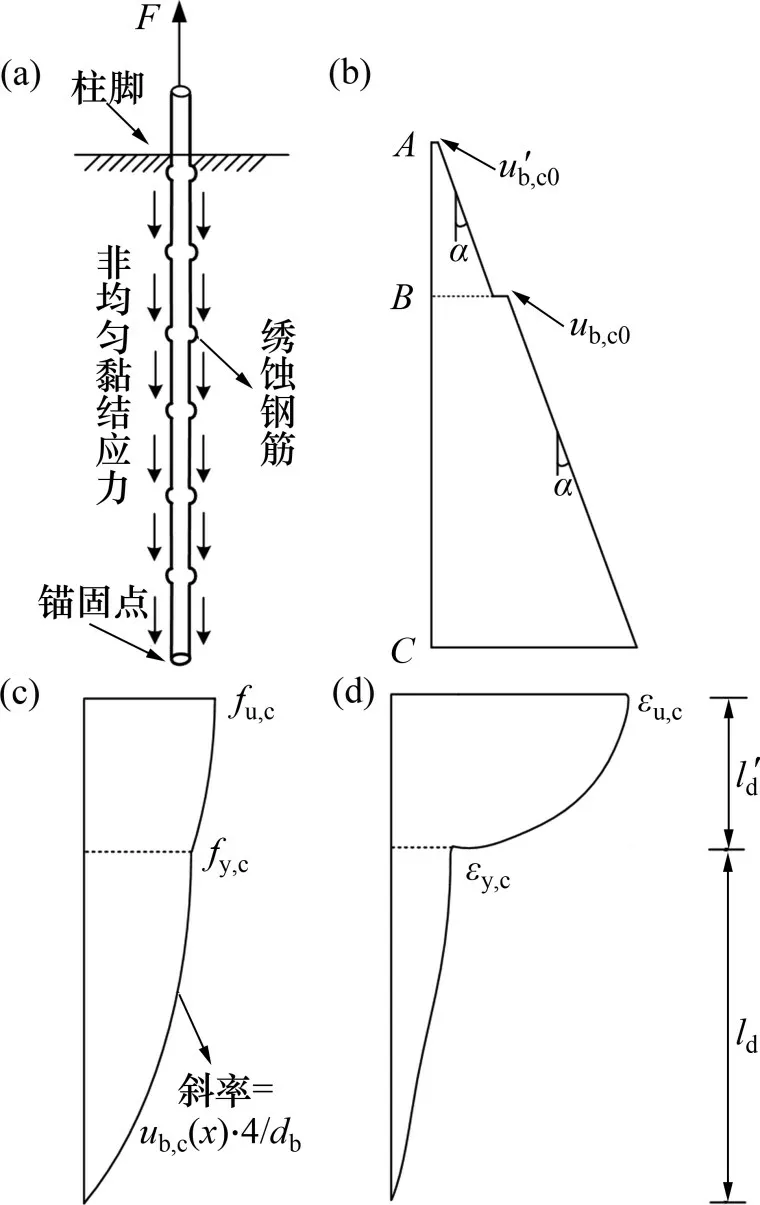
图7 锈蚀钢筋混凝土黏结滑移模型示意图Fig.7 Schematic of bonded slip model of corroded reinforced concrete
在该模型中,假设黏结应力沿锚固长度线性增加,根据文献[18−19],取单位长度黏结应力增量α为0.01,纵筋滑移弹性发展长度为ld,塑性发展长度为l′d。考虑钢筋锈蚀的影响,参考文献[20],定义初始黏结强度ub,c0为

基于黏结滑移试验层面验证本文提出的模型,参考文献[21],在分级加载的拉拔试验中测量了锈蚀钢筋应变沿锚固长度分布的情况,从而根据钢筋本构关系计算出钢筋应力的分布情况,得到沿锚固各区间的局部黏结应力。
图8所示为RC1-3试件不同荷载下钢筋应力分布对比图。由图8可见,采用该黏结滑移模型计算出的钢筋应力分布与试验测得的钢筋应力分布基本一致,二者与横轴所包围面积相差均不超过10%,且计算所得钢筋应力衰减至0 MPa所需的黏结长度相近,即说明计算钢筋应变分布符合较好,该模型可简化计算锈蚀钢筋与混凝土间黏结滑移效应。
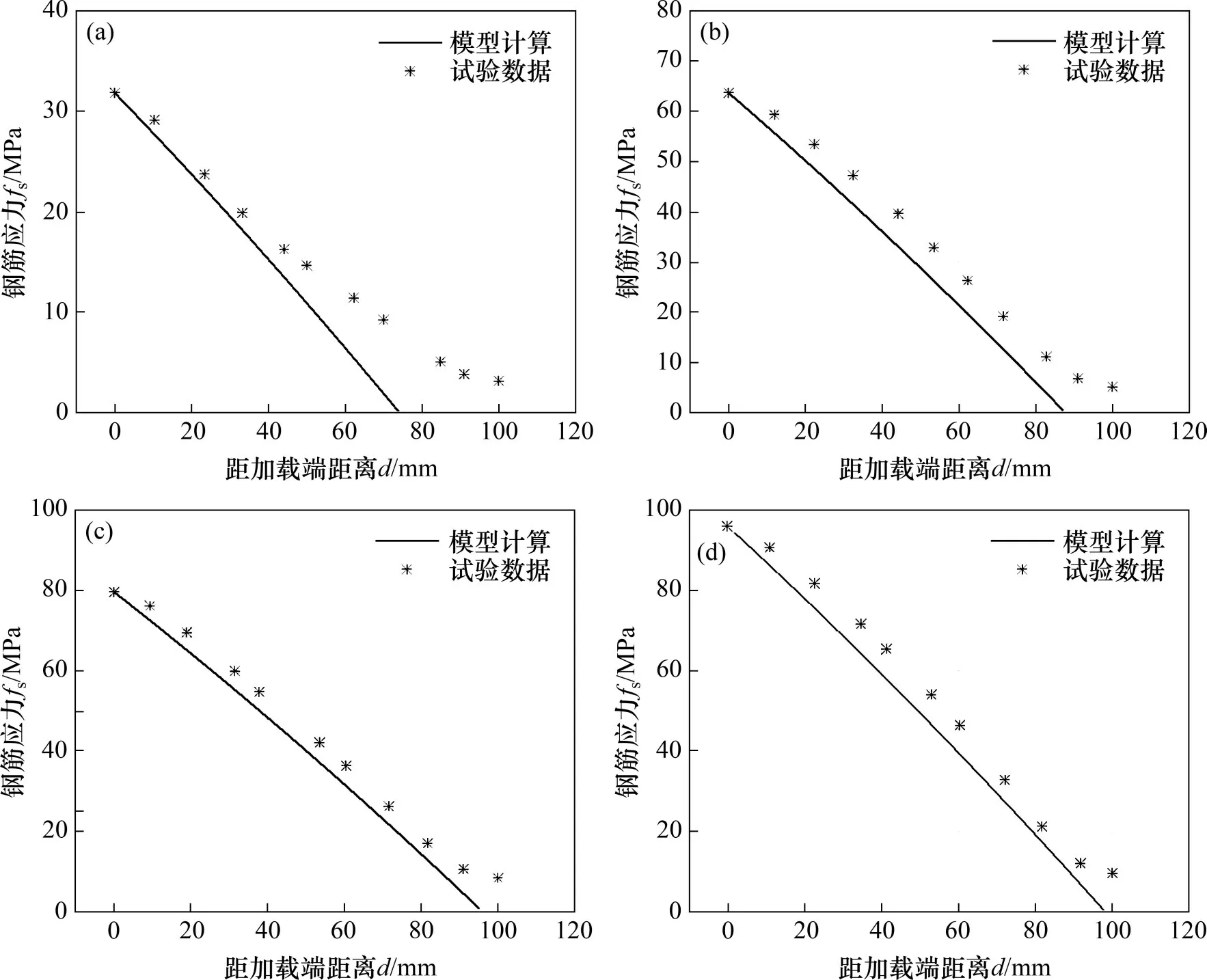
图8 RC1-3试件不同荷载下钢筋应力分布对比图[21]Fig.8 Comparison of stress distribution of steel bars under different load values of RC1-3 specimens[21]
3.3.2 纵筋滑移变形
RC 柱处于极限状态时,纵向钢筋已进入强化阶段,此时应按钢筋屈服应力将锚固长度划分为纵筋屈服前部分和屈服后部分,并分别计算2个部分滑移量,两者之和即为极限状态时纵筋与混凝土的相对滑移δslip。

式中:δslip,y为纵筋屈服前部分滑移量;δslip,u为纵筋屈服后部分滑移量。
纵筋屈服前部分(图7中BC段):根据B点钢筋荷载与沿BC段黏结力平衡的原则,计算钢筋屈服前锚固长度ld。

式中:fy为钢筋屈服强度;As,c为锈蚀钢筋截面面积;db为钢筋直径。
单位长度钢筋应力的变化量即为黏结力,由此可得
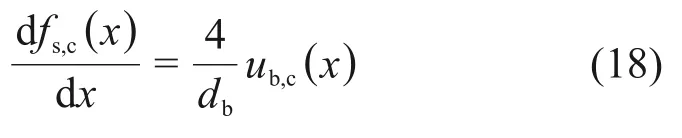
式中:fs,c(x)为BC段钢筋应力分布;ub,c(x)为BC段任意一点黏结应力。
以C为原点,考虑边界条件,对式(18)进行积分可得
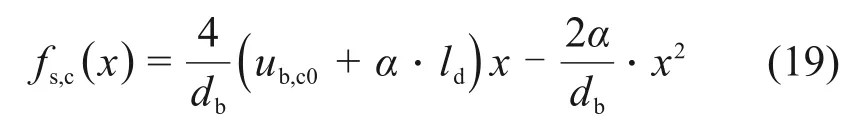
对式(19)进行积分,可以得到BC段钢筋的变形,即屈服前部分纵筋与混凝土的相对滑移δslip,y:
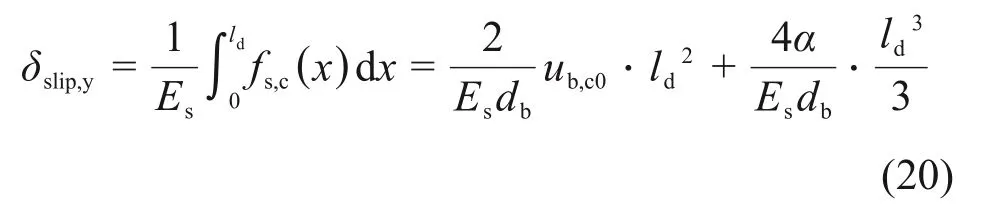
纵筋屈服后部分(图7中AB段):纵筋达到抗拉强度时,由A点和B点钢筋荷载与沿AB段黏结力平衡关系计算钢筋屈服后锚固长度l′d,计算公式如下:
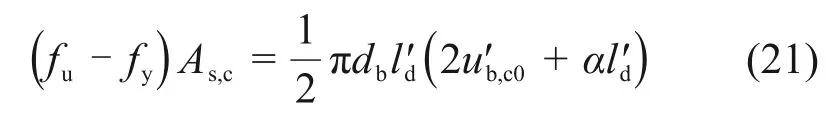
单位长度钢筋应力的变化量即为黏结力,由此可得
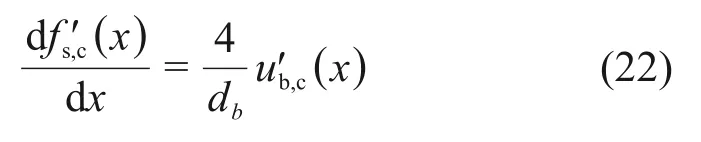
式中:f′s,c(x)为AB段钢筋应力分布;u′b,c(x)为AB段任意一点黏结应力。
以B为原点,考虑边界条件,对式(22)进行积分可得

进一步对式(23)进行积分,可以得到BC段钢筋变形即屈服后部分纵筋与混凝土的相对滑移为
式中:Esh为钢筋应变强化阶段弹性模量,取Esh=0.01Es。
3.4 等效塑性铰长度计算公式标定
根据曲率积分原理计算锈蚀RC柱的塑性转动能力,计算公式如下:
式中:θp为塑形转角。
根据前述分析与推导,得到考虑弯曲效应和纵筋滑移效应的锈蚀RC柱塑形转角θp为
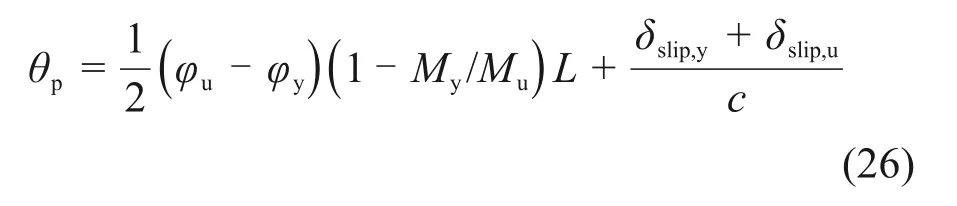
式中:c为截面受拉区高度,见图6。
对比式(25)与(26),代入式(20)与式(24),并考虑到εy/c等于屈服曲率φy,εu/c等于极限曲率φu,得到锈蚀RC柱等效塑性铰长度计算公式如下:


观察式(27)可知,式中除My/Mu外,其余参数均可根据试件设计参数及材料特性参数确定。PAULAY 等[4]指出,弯矩超强系数Mu/My的主要控制因素为纵筋配筋率ρl,故(1-My/Mu)与纵筋配筋率ρl相关性较强。本文以郑山锁等[7]使用的C-4试件为基准,设计不同纵筋配筋率截面,通过截面P−M−φ分析,分别以截面受拉侧纵筋屈服和承载力降至峰值承载力85%时定义截面屈服弯矩My和极限弯矩Mu,并将纵筋锈蚀简化为纵筋截面积削减,得到(1-My/Mu)拟合公式:

式中:λcorr为纵筋锈蚀率;ρl为纵筋配筋率。
为保守估计柱底附加转动,并进一步简化等效塑性铰长度表达式,将fu/fy近似取1.5,将ub,c0+近似取ub,c0+⋅ld,将u′b,c0+⋅ld′ 近似取u′b,c0+⋅ld′,同时将式(16),(21)和(28)代入式(27),最终得到锈蚀RC 柱等效塑性铰长度计算公式:
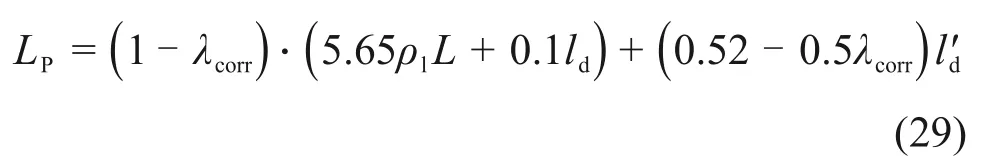
式中:ld为纵筋滑移弹性发展长度,根据式(16)确定;l′d为纵筋塑性发展长度,根据式(21)确定。
4 试验验证
基于文献[7]中的7榀锈蚀RC柱拟静力试验结果,对本文所建立的锈蚀RC柱等效塑性铰长度计算公式进行验证,表1所示为文献[7]中各试件主要设计参数。
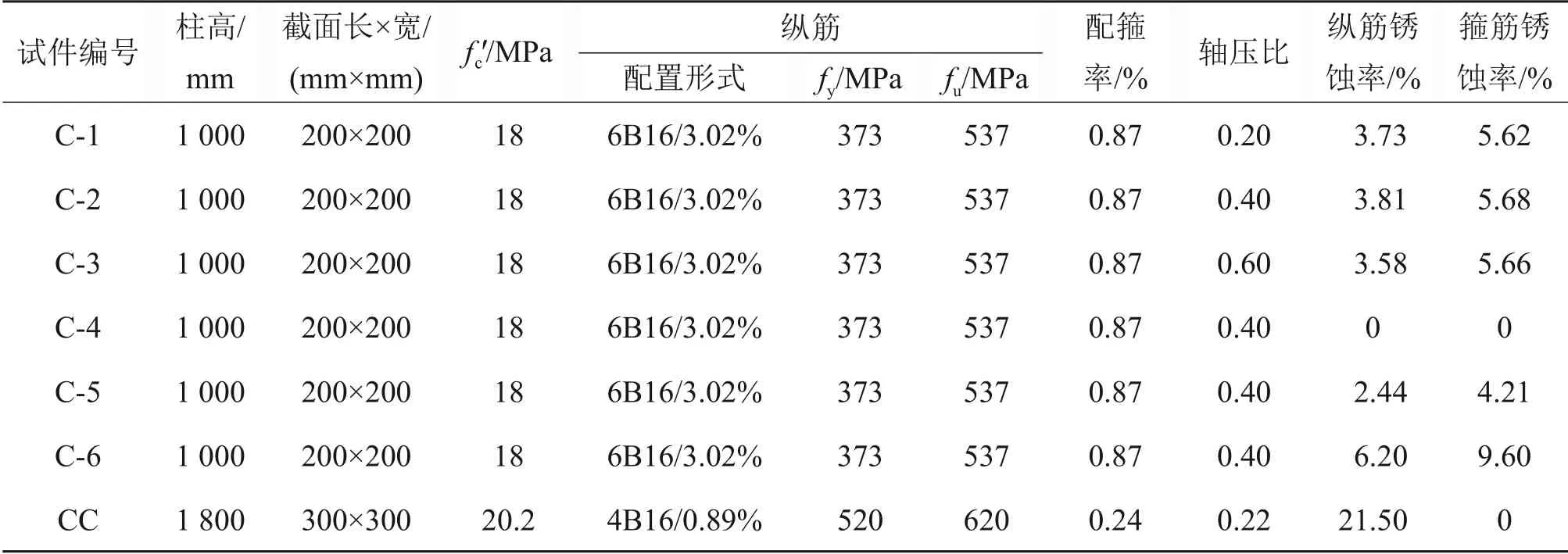
表1 RC柱主要设计参数Table 1 Main parameters of RC columns
4.1 等效塑性铰长度计算值与试验值验证
在式(3)基础上推导锈蚀RC柱试验等效塑性铰长度,其计算公式如下:
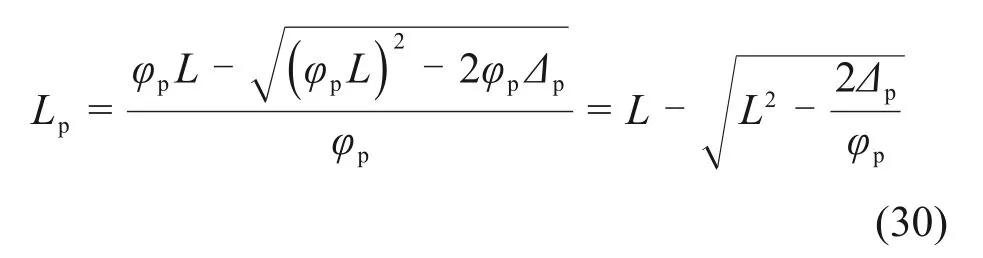
根据式(30)可以看出,若已知柱高L、柱顶塑性位移Δp和塑性曲率φp,则可得到相应的试验等效塑性铰长度。
1)确定塑性曲率φp。目前试验中采用位移法量测的截面平均塑性曲率包含弯曲效应以及纵筋滑移效应,而根据塑性铰长度定义可知,柱体弯曲效应与纵筋滑移效应已在塑性铰长度计算公式中考虑,本文在推算试验塑性铰长度时,假定与之匹配的是纯弯曲曲率,故塑性曲率通过截面P−M−φ分析获取。
2)确定塑性位移Δp。需先确定柱顶极限位移Δu与屈服位移Δy。极限位移Δu取柱顶荷载−位移骨架曲线下降段中侧向力降至峰值承载力的85%时对应的位移;为与塑性曲率φp相匹配,屈服位移根据截面P−M−φ分析所确定的φy计算得到,即Δy=φyL2/3。
图9所示为等效塑性铰长度计算值与试验值的对比。从图9可见:等效塑性铰长度计算值与试验值相对误差基本不超过20%,两者间线性相关系数高达0.96,这表明采用本文建议公式所得锈蚀RC 柱等效塑性铰长度计算值与试验值吻合程度较好。

图9 Lp计算值与试验值对比Fig.9 Comparisons between calculated and test values of Lp
4.2 柱顶侧向力−位移关系验证
定义等效塑性铰长度是准确估计锈蚀RC柱在地震荷载作用下的塑性变形能力的基础,其计算结果的准确性也应通过试验结果进行验证。基于等效塑性铰长度的柱顶荷载−位移计算方法进行如下假设:
1)柱底屈服前其整体处于弹性变形阶段,根据式(31)计算柱顶位移;
2)柱底屈服后即出现塑性铰,并假定塑性铰长度保持不变,根据式(31)计算柱顶位移;
3)考虑P−Δ效应,通过式(32)计算不同柱顶位移Δ对应的柱顶荷载,即可得到RC 柱侧向力−位移计算曲线。
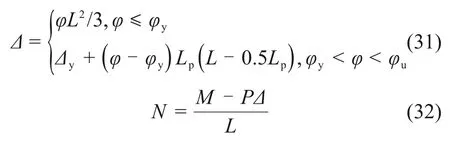
式中:P为轴压力。
可以看出,计算结果与试验结果吻合较好,进一步说明本文所建立的锈蚀RC柱等效塑性铰长度计算公式能够准确反映构件塑性变形能力,并结合柱顶荷载−位移计算方法,可较准确预测构件在水平荷载作用下的侧向力−位移骨架曲线。
5 结论

图10 柱顶荷载−位移曲线计算值与试验值对比Fig.10 Comparisons between calculated values and test values of force−displacement curves
1)钢筋锈蚀将导致保护层开裂、箍筋约束能力降低,并劣化钢筋与混凝土间黏结性能。计算弯曲破坏锈蚀RC柱等效塑性铰长度时应考虑弯曲变形和纵筋滑移变形,并考虑钢筋锈蚀对混凝土、钢筋力学性能及混凝土与钢筋间黏结性能的影响。
2)定义了钢筋屈服前和屈服后的锈蚀黏结强度,并基于两段式黏结应力分布简化模型建立了锈蚀钢筋混凝土黏结滑移模型。
3)基于曲率积分原理建立了包含锈蚀程度、柱高、纵筋配筋率与材料特性等参数的锈蚀RC柱等效塑性铰长度计算公式,并在等效塑性铰长度与柱顶侧向力−位移关系2 个方面验证了计算公式的准确性。

