重点目标防空作战中多预警机协同探测空域配置 *

祁 炜，蒋 伟，武 文，程东升

(空军预警学院 防空预警装备系， 湖北 武汉 430019)

针对重点目标进行防空作战时，多预警机协同探测可提供充足的对空抗击作战组织时间和引导战机对敌实施空中拦截[1-6]，而预警机属于较为稀缺的重要作战力量，因此如何在有效遂行防空作战任务的前提下，合理筹划空域配置和出动兵力已成为急需解决的预警机任务规划核心问题。

相关文献对预警机的探测性能进行研究，如文献[7]分析了单架预警机在不同巡逻航线下的探测性能参数，并针对不同环境条件的特点，给出了预警机巡逻航线的建议，但未涉及预警机与重点目标之间的位置关系；文献[8]以某岛礁要地作战为仿真背景，构建了多预警机最大和最小前出距离的仿真模型，为预警机前出距离的选择提供理论依据，但无法满足威胁角较大时多预警机如何协同的问题；文献[9]从战术层面，构建了一套预警机巡逻策略制定系统，为指挥员在遇到上级任务命令时，制定巡逻策略提供案例依据，但未给出预警机在巡逻空域的量化估算模型。文献[10]从动态和静态两个层面，构建了多预警机雷达效能评估模型，为战时任务规划提供指导依据。上述文献均未涉及多预警机协同探测时并立航线和串接航线如何转换，最少出动兵力如何确定等问题。

本文首先明确了重点目标预警线划分方法，根据预警机防空作战的具体任务，构建其阵位选择量化模型，并以此为基础在确保自身安全且充分发挥预警机固有探测威力的前提下，提出了一种多预警机并立航线和串接航线空域配置量化模型，可为预警机作战部队日常训练、演习演练和对空抗击作战提供空域配置的理论依据。

1 问题描述

1.1 预警线划分

预警机在进行空域作战时，可以以重点目标为圆心，以相对应的防空预警线为半径画圆弧，三条圆弧可设定为三条防空预警线，三条预警线之间以及预警线与直径围成的区域分别为相应的内层防空预警区、中层防空预警区和外层防空预警区[11-13]，防空预警区域划分如图1所示。

图1 防空预警区域划分图Fig.1 Division of air defense early warning area

内层防空预警区是指内层防空预警线与直径组成的区域，其主要由导弹拦截区和交叉区组成，该区的主要任务是由各种导弹发射平台在我方各类侦察设备的指引下对敌方导弹进行拦截；中层防空预警区是指内层防空预警线与中层防空预警线之间的区域，其主要由探测跟踪区与战斗机交战区组成，主要任务是由我方预警机对敌方装备进行探测与跟踪，并指引我方战斗机进行空中拦截与交战；外层防空预警区是指中层防空预警线与外层防空预警线之间的区域，该区主要依靠卫星等其他传感器进行情报协同[14-16]。

1.2 中层预警线计算模型

由于中层防空预警区的空情保障任务主要由预警机执行，因此确定预警机阵位，就要首先估算中层防空预警线与重点目标之间的距离Dzz。图2为威胁角防空区域图，由图2可知，Dzz的估算公式为：

Dzz=Dzx+dyx+dtg

(1)

式中：Dzx是重点目标到一次拦截近界的距离；dyx是巡逻机拦截线和一次拦截近界的距离；dtg是中层防空预警线和巡航机拦截线的距离。为了提供尽可能多的预警时间，Dzx取最大前置距离：

Dzx=V(txh-tcb-txs)/2

(2)

式中：V是战斗机巡逻速度；txh是战斗机平均续航时间；tcb是战斗机准备时间；txs是指挥机构要求的战斗机巡逻飞行时间。

图2 威胁角防空区域图Fig.2 Threat angle of air defense area

在敌战斗机进入内层防空预警线前，上级指挥机构要求战斗机必须进行一次以上的空中拦截，因此Dzx必须满足如式(3)所示的约束条件。

(3)

其中：Dnc是内层防空预警线距离；Dd1是导弹拦截线距离；djc是交叉区覆盖距离；Djq是导弹防御线半径；djk是导弹最大射程；dkd是敌方战斗机最大攻击距离；t1是预警机与己方远程警戒雷达目标探测交接时间；t2是远程警戒雷达与目标指示雷达目标探测交接时间；t3是目标指示雷达与制导雷达之间的交接时间；t4是制导雷达捕获、跟踪目标所需时间；t5是面对空导弹发射准备时间；t6是导弹空中飞行时间；t6=djk/vjk，vjk是导弹平均飞行速度；t7是误入交叉区的战斗机撤出时间。

为有效引导己方战斗机对敌战斗机进行拦截，上级要求己方预警机必须具有一定的提前预警距离，即

(4)

式中：VT是敌方战斗机巡航速度；t8是目标从探测到跟踪所需时间；t9是上级下达己方战斗机进行空中拦截所需时间。

将式(2)、式(4)代入式(1)可得：

(5)

2 阵位线选择

预警机在阵位选择时应遵循的基本原则是：在确保自身安全的前提下，充分发挥其最大探测性能。因此，预警机必须处于敌战斗机最大射程区域之外。假设敌战斗机最大攻击距离为djkk，预警机接到命令撤回到Dd1-djkk所需间隔距离为dg1，则预警机阵位D′zy可由下式确定：

(6)

所需间隔距离dg1应以可能遇到的最极端情况进行考虑，即当预警机直飞航线与威胁轴处于重合时，敌战斗机通过一次拦截近界，dg1可用估算公式表示为：

(7)

式中，WY定义为转弯直径。

(8)

式中，βY是预警机最大转弯角度，g是重力加速度。

将式(7)和式(8)代入式(6)可得：

(9)

预警机实际阵位Dzy最终可表示为：

(10)

3 兵力估算与部署间隔

3.1 并立航线

预警机在采用双平行线形或横8形巡逻航线样式时，实时探测覆盖范围相同[17]。因此，本节以双平行线形为例，构建数学模型，所建模型可应用于横8形巡逻航线样式。

多预警机拱形任务线协同覆盖情况如图3所示，不失一般性，令多预警机协同遂行预警探测任务，第i架预警机巡逻直飞航线四个端点分别为AYi、BYi、CYi和DYi，且直飞航线长度|AYiBYi|=|CYiDYi|=LYi=2ai、转弯直径|AYiCYi|=|BYiDYi|=WYi=2bi。当多预警机采用并立航线对任务扇面角αtx遂行协同预警探测任务时，均以Ei-1为坐标系原点，且Y轴垂直于预警机巡逻直飞航线，而构建XEi-1Y直角坐标系。

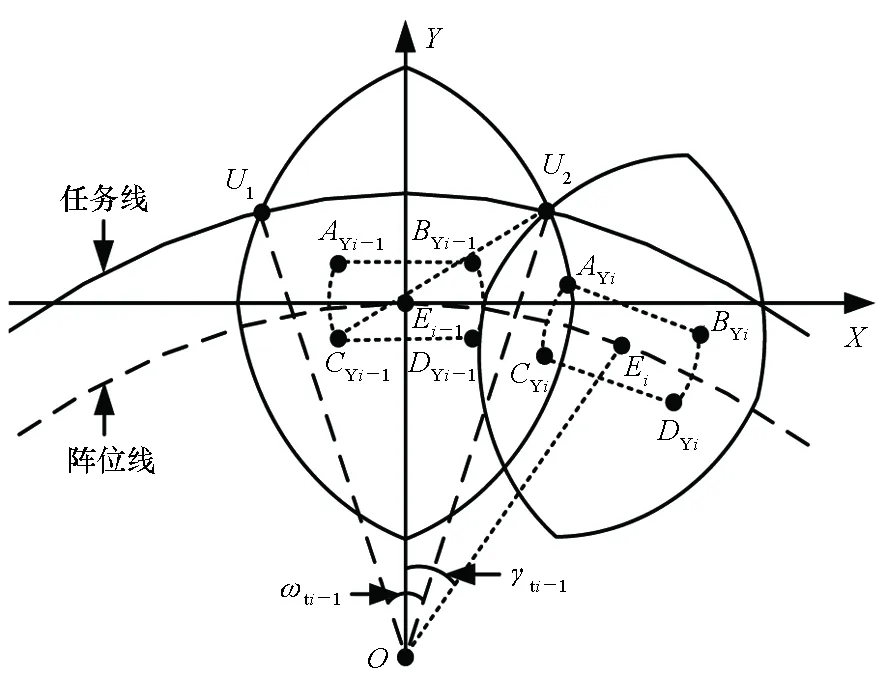
图3 多预警机拱形任务线协同覆盖示意图Fig.3 Cooperative coverage diagram of arched mission lines of multiple early warning aircraft

多预警机协同空域配置态势如图3所示，U1是以DY(i-1)为圆心、以Rmax(i-1)为半径的实时探测边界和任务线的交点，U2是分别以CY(i-1)和DYi为圆心、以Rmax(i-1)和Rmax为半径的实时探测边界交点，且与任务线重合，则∠U1OU2=ωt(i-1)，∠Ei-1OEi=γt(i-1)，显然|OU1|=|OU2|=Rtx、|OEi-1|=|OEi|=dtx，联立方程组：

(11)

可求得U2点坐标(xU2,yU2)，则第i-1架预警机单独覆盖任务线对应O点角度ωt(i-1)和第i-1与i架预警机之间空域配置角γt(i-1)为：

(12)

因此，当任务扇面角为αtx时，所需预警机同时出动架数n的约束条件为：

(13)

3.2 串接航线

当重点目标威胁角过大或全方位受到威胁时，预警机可根据具体情况选择圆形串接巡逻航线样式遂行情报保障任务。当预警机与目标接近时，由于要立马回撤，需要较大的转弯半径，会造成转弯盲区；当预警机与目标之间的距离较远时，单架预警机无法完成指定任务，需要在航线上部署多架预警机进行系统探测[18]。单架预警机防空区域如图4所示，不失一般性，令作战性能相同的多架预警机协同遂行防空作战任务，其相同高度层探测距离均为Rmax。以重点目标O为圆心，预警机阵位线到重点目标距离为Dzy。以重点目标O为坐标系圆点，令某一时刻第一架预警机阵位A1与坐标圆点连线为X轴，过O点垂直于X轴的坐标轴为Y轴，建立XOY直角坐标系。

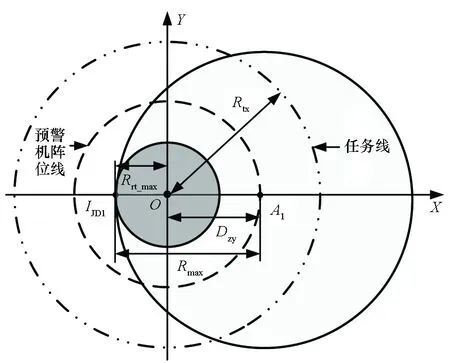
图4 单架预警机防空区域图Fig.4 Air defense area diagram of single early warning aircraft

令预警机阵位线上有N架预警机同时遂行防空作战任务，则实时探测区外边界和内边界到O点距离分别为Rrt_max和Rrt_min，其估算模型可分为N=1和N≠1两种情况进行讨论。

对实时探测区外边界Rrt_max进行讨论：单架预警机(N=1)遂行防空作战任务时，如图4所示，Rrt_max为：

(14)

多架预警机(N≠1)协同作战时的防空区域如图5所示。为获得最大实时探测区域，令N架预警机两两相邻等间隔部署在预警机阵位线上，则相邻预警机与O点连线的夹角为：

β=2π/N

(15)

图5 多预警机协同防空区域图Fig.5 Cooperative air defense area diagram of multiple early warning aircraft

不妨令第一架预警机阵位点坐标为(Dzy,0)，则第二架预警机阵位点坐标为(Dzycosβ,Dzysinβ)。多预警机串接协同探测时，令以A1为圆心、以Rmax为半径的第一架预警机探测范围与以A2为圆心、以Rmax为半径的第二架预警机探测范围交于(x,y)。则可得方程组：

(16)

相邻两预警机存在实时探测区的约束条件为：

(17)

通过式(16)可解得IJD1(x1,y1)，IJD2(x2,y2)交点坐标为：

(18)

则N架预警机协同的实时探测区外边界Rrt_max为：

(19)

而实时探测区内边界Rrt_min需进一步讨论。如图5所示，显然，当预警机架数N=1,2且Dzy>Rmax时，不存在实时探测区内边界，只存在无实时探测区的情况；当N≥3时，由于预警机阵位距离重点目标较远，使得IJD2处于预警机阵位与重点目标之间，致使重点近距离存在半径为Rrt_min的圆形实时探测盲区。

(20)

此时需通过其他情报感知力量对以O点为圆心，Rrt_min为半径的圆形区域进行协同补盲，以确保有效遂行任务线内空域的空情保障任务。

综合式(14)、式(17)～(20)可得：

(21)

(22)

因此，当预警机遂行任务线半径为Rtx的空情保障任务时，至少需要同时出动N架预警机的约束条件为：

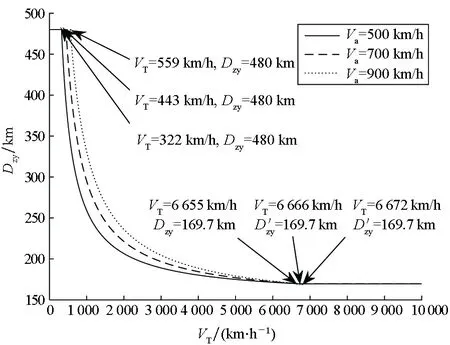
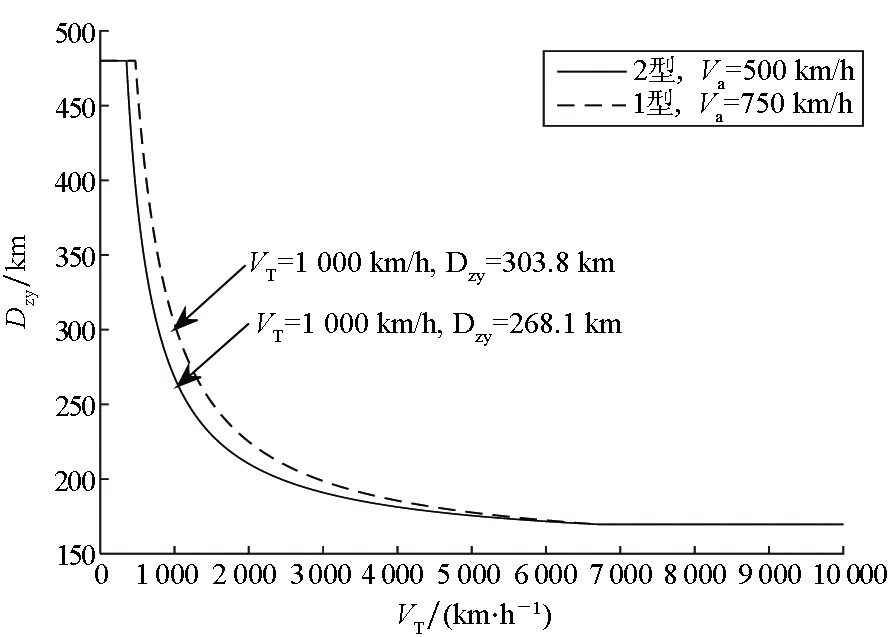
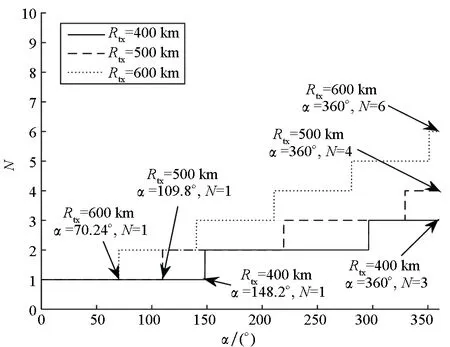
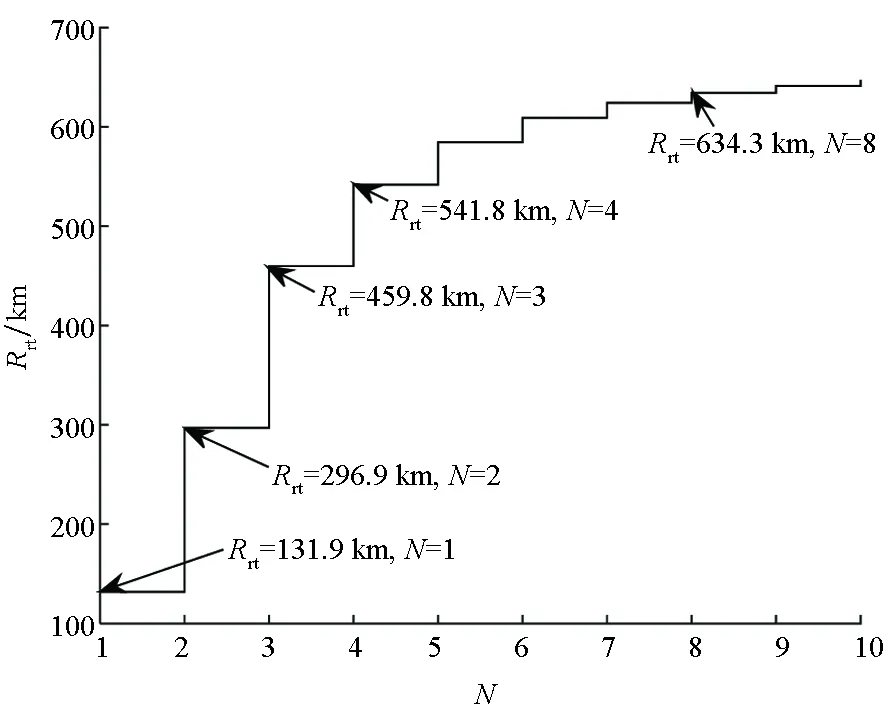
Rrt_maxN-1

(23)

4 仿真分析

本节主要从预警机阵位对比和架数选择两个方面进行分析，合理设定攻防双方具体参数的前提下，分别对第2节与第3节得出的重要结论进行仿真验证。

攻防双方参战飞机及其配属装备、导弹性能参数和各作战流程消耗时间等如表1所示[19]。

表1 重点目标防空作战相关参数设置

4.1 阵位对比分析

根据国外几种典型预警机的相关数据，令Va={500,700,900}km/h，且设敌战斗机飞行速度VT∈[1,10 000]km/h，则可得图6所示的VT与Dzy之间的关系曲线。由图6可得以下结论：

1)VT≤{322,443,559}km/h时，Dzy=Dzx=480 km，即此时预警机阵位可前伸至巡逻战斗机的阵位，且Va越大预警机实际阵位开始后置于巡逻战斗机阵位时的VT越大；

2)169.7 km

3)VT≥{6 655,6 666,6 672}km/h时，Dzy=Ddl-djkk=169.7 km，即此时按式(2)～(4)计算预警机阵位已处于Ddl-djkk之内，为了充分发挥实时探测区的效能，预警机可停留在Ddl-djkk处，从而Dzy达到最小值。

图6 VT与Dzy关系曲线Fig.6 Relation of VT and Dzy

4.2 部署架数对比分析

假设某1型和2型预警机相关参数如表2所示，其余参数同表1。

表2 1型和2型预警机参数

其中，Rmax1、Rmax2分别是预警机正常模式与增程模式时的探测距离。两型预警机VT与Dzy关系曲线如图7所示，当敌机飞行速度VT=1 000 km/h时，两型预警机的阵位距离分别为303.8 km和268.1 km。

图7 两型预警机VT与Dzy关系曲线Fig.7 Relation of VT and Dzy of two early warning aircrafts

4.2.1 并立巡逻航线架数分析

令Dzy=268.1 km、Rtx∈{400,500,600}km、威胁角α∈[0°,360°]，且环境因素、预警机的探测能力以及预警机航线样式均保持与上述相同，则完成指定探测任务所需的预警机架数N与威胁角α的关系如图8所示。

分析图8可知:

1)当任务线Rtx=500 km时，单架预警机在正常模式和增程模式覆盖α角度分别为87.81°和109.8°。这说明在相应工作模式下当α≤87.81°和α≤109.8°时，单架预警机就可独立完成空域探测任务，无须和其他预警机进行协同；预警机使用增程模式覆盖α角度远大于正常模式。因此，在预警机资源紧张且威胁角α较大时，正常模式中单预警机无法有效完成作战任务，可改变工作模式。

2)当任务线Rtx=600 km且覆盖角度α=360°时，正常模式需要9架预警机，而增程模式只需要6架，可比前者节约3架预警机资源。但使用增程模式将导致数据率降低，增加预警机跟踪探测敌机的时间，此时指挥员需权衡探测距离与跟踪探测时间对作战任务的影响。

3)分析图8(a)可知，正常模式中当Rtx={400,500,600}km时，部署架数N={3,5,9}；同时分析图8(b)可知，增程模式中当Rtx={400,500,600}km时，部署架数N={3,4,6}。对比两种工作模式所需预警机架数，随着任务线Rtx增大，增程模式比正常模式节约预警机资源的效果越明显。

4)由8(a)可知，当任务线Rtx=500 km且威胁角在351.3°<α≤360°时，第5架预警机与第1架预警机之间已可通过相互协同有效遂行作战任务；当任务线变化时，协同作用仍然成立。

(a) 正常模式α与N的关系(a) Relation of α and N under the normal mode

(b) 增程模式α与N的关系(b) Relation of α and N under the extended mode图8 α与N的关系Fig.8 Relation of α and N

4.2.2 串接巡逻航线架数分析

令Rmax=400 km、Dzy=268.1 km，ΔRrt_add=Rrt_maxi-Rrt_maxi-1，ΔRrt_add是多增加一架预警机获得实时探测区外边界的增加距离值，可用于评估多增加一架预警机所获得的收益。且环境因素、预警机的探测能力以及预警机航线样式均保持与上述相同，则预警机实时探测距离Rrt的关系对比如图9所示。

(a) N与Rrt关系曲线(a) Relation of N and Rrt

(b) N与ΔRrt-add关系曲线(b) Relation of N and ΔRrt-add图9 串接巡逻航线Rrt关系对比Fig.9 Contrast relation of Rrt in tandem patrol route

根据仿真结果可以得出以下几点结论：

1)分析图9(a)可知，当1架、2架、3架、4架预警机遂行作战任务时，以重点目标为圆心，预警机构筑的实时探测预警圈半径分别为Rrt1=131.9 km，Rrt2=296.9 km，Rrt3=459.8 km，Rrt4=541.8 km；此时令敌方战斗机飞行速度为1 000 km/h，则为我方提供的防空作战准备时间分别为7.91 min、17.81 min、27.58 min、32.5 min，因为预警机是防空作战中重要的稀缺资源，所以在有效遂行防空作战任务的前提下，尽量减少预警机同时升空架数，可有效保存守方预警机力量。因此，进一步加强地面人员之间的配合程度或提升武器装备性能、缩短反应时间，是一个行之有效的方法。

2)分析图9(b)可知，预警机架数N与实时探测距离Rrt的关系呈先递增后递减的趋势。当预警机架数为2时，此时实时探测距离增值取得最大值，即ΔRrt_add_max=165 km，此时增加预警机架数的收益最大。

3)综合图9(a)、(b)可知，随着任务线Rtx增加，所需预警机架数呈指数上升趋势，此时采用串接巡逻航线对预警机资源占用巨大，当预警机架数超过4时所获得的收益非常小。

4)比较图8(a)和图9(a)可知，以预警半径为500 km时为例，当威胁角263.4°≤α≤351.2°时，采用并立航线所需的预警机架数为4，当威胁角351.2°<α≤360°时，采用并立航线所需的预警机架数为5；而采用串接航线时，它是360°全覆盖的，所需的预警机架数为4。因此当威胁角α≥263.4°时，采用串接航线。以预警半径为500 km时为例，当威胁角α<263.4°时，采用并立航线所需的预警机架数≤3；而采用串接航线时，它是360°全覆盖的，所需的预警机架数为4。因此当威胁角α<263.4°时，采用并立航线。

5 结论

本文构建了预警机阵位选择量化模型，在此基础上，提出了预警机不同巡逻航线样式的空域配置量化决策模型，所得结论主要有以下几点：

1)当威胁角大于等于某一角度时，并立航线与圆形串接同时升空预警机架数相同，此时应选择圆形串接航线，以获得更加良好的战场适应性；当威胁角小于这一角度时，采用圆形串接航线所消耗的预警机资源大于并立航线，因此在该情况下应选择并立航线进行协同探测。

2)当守方空中预警机资源有限，且预警线距离重点目标较远时，可将预警机工作模式切换到增程对空探测模式，但也会导致预警机数据率降低。

3)当采用圆形串接航线时，预警机实时探测距离随着预警机数量增加而增加，但当预警机数量增加到一定数量时，此时所获得的实时探测距离增益越来越小。因此，在对预警机架数进行选择时，应充分考虑每增加一架预警机所获得的收益。