航空集群机载网络Failure-Oblivious路由策略 *
吕 娜,潘 颖,朱梦圆,陈 坤,方 宇
(空军工程大学 信息与导航学院, 陕西 西安 710077)
随着网络化集群作战[1]理念在航空作战领域的深入,受生物集群[2]启发,航空集群[3]作为一种全新的航空作战力量体系应运而生。航空集群在引发未来空战样式深刻革命[4]的同时,也给保障集群成员间通信的机载网络[5]带来诸多技术难题。
如图1所示,航空集群机载网络采用无线通信技术连接不同类型、功能各异的有人或无人空中平台,实现了作战平台、指控平台、传感器平台、武器平台等各类平台战术信息资源网络化,本质上是一种大规模异构数据链网络[6]。由于空中平台通信半径有限,集群成员间通信需经过多跳转发完成,因此路由策略是值得研究的问题。

图1 航空集群机载网络Fig.1 Airborne network for aeronautic swarm
航空集群机载网络的特殊性给路由策略的研究带来挑战。其路由策略除了要适应多跳、自组织等机载网络普遍特征外,还应关注航空集群机载网络的以下特点:
1)编队拓扑变化具有不确定性。航空集群作战能力的涌现依赖于面向作战任务的构型控制及演化[7],即根据实际作战任务需求临时组建任务编队。由于作战任务突发性强,航空集群机载网络拓扑结构变化并无明显规律。
2)通信连通状态具有不确定性。航空集群机载网络节点机动性强,高速移动过程中极易超出邻居节点电波通信覆盖范围,通信暂盲[8]现象时有发生。
3)链路通信质量具有不确定性。拒止空间复杂电磁对抗环境下,“战争迷雾”的存在使得航空集群机载网络中每条链路均有可能受到敌方干扰机不同程度的干扰,链路通信质量波动较大。
上述不确定性使得路由失效成为航空集群机载网络路由策略必须面对的挑战之一。
为应对路由失效问题,近年来已有学者提出通过移动位置预测[9-10]及干扰感知检测[11]等技术手段,获取更多网络状态信息,提高路由策略的可靠性。但由于获取信息需要一定的时间,并不能很好地保证路由策略的时效性。此外,航空集群机载网络中存在诸多不确定性因素,网络状态信息难以被准确预测和精确感知,给上述方案的实际应用带来困难。现有路由策略无法完全满足航空集群机载网络严苛的性能需求,如何在信息受限的不确定环境下兼顾信息传输实时性与可靠性,是航空集群机载网络路由策略亟须解决的问题。
软件定义航空集群机载网络[12]的提出,给路由策略的研究带来机遇。利用其集中控制功能和全网统一视图,有助于路由策略摆脱传统网络分层协议栈的束缚[13],使得全局最优路由策略的实现成为可能。从现有文献来看,对软件定义航空集群机载网络路由策略的研究多集中于网络更新[14]方面,对路由选择算法的研究不够充分。
基于此,在软件定义网络架构下,从路由选择算法的角度,为航空集群机载网络设计一种能兼顾实时性与可靠性的Failure-Oblivious路由策略。该策略根据控制平面提供的网络拓扑图为各节点对计算多条随机路由,即使其中部分路由失效,其余未失效路由仍能保障正常通信。
1 相关研究
路由策略的关键在于路由选择算法的设计[15],路由选择算法计算生成路由质量直接影响网络端到端的通信质量[16]。依据路由策略所采用路由选择算法的不同,常见的多路径路由策略主要有以下三种:
1)最短路由策略。最短路由策略采用K条最短路由(K-Shortest Paths, KSP)[17]选择算法进行路由决策。值得注意的是,这里的最短并不一定指实际通信距离最短,而是通信代价最低[18],即通过定义链路代价函数确定拓扑图中各边权值,反映通信距离、跳数、时延[19]、流量[20]、拥塞程度[21]等开销,将路由求解转化为一个最优化问题。
此类路由策略可使某些性能指标达到最优化,但由于最优解会随网络参数的变化而改变,对于动态变化的网络,路由算法往往不能及时收敛。此外,对于链路资源有限的网络,采用最短路由策略会使流量相对集中地分布于最短路由“瓶颈”上,导致网络中某些链路负载过重,存在加剧通信故障的风险。
2)不相交路由策略。不相交路由策略采用边不相交路由(Edge-Disjoint Paths, EDP)[22]选择算法或点不相交路由(Vertex-Disjoint Paths, VDP)[23]选择算法进行路由决策。边不相交路由选择算法可以降低链路失效风险[24],点不相交路由选择算法可以减少单点故障的影响。
此类路由策略鲁棒性较强,但严格不相交的约束条件提高了路由的代价下限。同时,对于某些网络拓扑而言,并不一定能够寻找到完全不相交的多条路由。
3)Oblivious路由策略。Oblivious路由策略也称Demand-Oblivious路由策略[25],采用Oblivious路由选择算法计算路由。Oblivious路由选择算法可在通信流量需求产生之前完成路由决策,并为网络各节点对间规划出多条随机路由,具有灵活、简洁等优势。Oblivious路由选择算法设计之初旨在实现负载均衡性能,其主要思想是在无法精确掌握节点间流量需求的情况下,从博弈论的层面给出能够应对随机突发流量的路由策略。主要分为以下两类:
一是由Valiant等[26]提出的Valiant负载均衡(Valiant Load-Balancing, VLB)路由选择算法。主要思想是在待通信节点对之间增设一个在全网范围内随机选取的中间节点,分两步进行路由:先选择一条以中间节点为目的节点的随机路由,再选出从该中间节点到目的节点的随机路由。该算法巧妙利用随机选取的中间节点分散负载压力,从而降低网络拥塞[27];但缺点是路由代价不可控,且只适用于超立方体网络、Mesh网络、骨干网[28]等特定结构的网络拓扑。
二是Räcke于2002年首次提出基于层次分解树的Oblivious路由策略[29],可用于任意网络拓扑结构。但其算法的求解属于NP难度问题,无法在多项式时间内求解路由;2004年,Azar等[30]和Räcke给出了一种能够在多项式时间内求解最佳路由的算法,但此算法需要借助椭圆算法,处理数量无穷大的约束条件方程,复杂度仍较高;2008年,Räcke[31]指出利用FRT(Fakcharoenphol, Rao and Talwar)图嵌入算法[32]等近似算法能够快速、高效生成随机层次分解树;2020年,Czerner和Räcke提出了一种能够节约路由表存储空间、具有高性能比的Oblivious路由策略[33]。
基于上述两类经典Oblivious路由选择算法,其他相关研究人员沿袭Valiant和Räcke等的研究思路,对Oblivious路由策略进行了一系列的优化改进和创新。例如,文献[34]提出基于VLB的两阶段路由,为任意拓扑结构的网络提供了通用Oblivious路由方案;Harrelson等[35]提出了一种改进的图分割算法,可在多项式时间内获取具有近乎等价通信特性的路由树;Applegate等则提出可用有限变量线性规划方程求解的最优化路由算法[36],与椭圆算法相比,其运算时间、空间复杂度大大降低。
当然,Oblivious路由策略也存在一些固有缺陷。由于其不考虑路由代价,在进行路由选择时具有一定盲目性,对于性能要求严苛的网络并不适用;由于其具有较强随机性,Oblivious路由选择算法在运行过程中会出现路由不连通等问题,致使路由选择算法有时会因此停滞,不得不返回上一步循环来寻找连通路径。
新的研究表明,将流量工程与Oblivious路由策略相结合,二者优势互补设计Semi-Oblivious路由策略,不仅可有效均衡负载[37],还可以低开销获得近乎最佳的网络性能,且能够应对突发流量和意外的链路故障[38]。文献[39]则通过深入的仿真和在SDN硬件上的部署,进一步验证了Semi-Oblivious路由策略具有可与SWAN[40]等先进流量工程路由策略相比拟的性能。
受此启发,既然Demand-Oblivious路由策略可以在不掌握流量需求的情况下应对随机突发流量,那么是否也存在Failure-Oblivious路由策略,可在链路通断不确定条件下应对路由失效问题?在此问题驱动下,将最短路由策略与Oblivious路由策略相结合,设计航空集群机载网络Failure-Oblivious路由策略,以期兼顾通信实时性与可靠性。
2 Failure-Oblivious路由策略
2.1 基本思想
采用数学语言,对Failure-Oblivious路由策略(以下简称FOR路由策略)基本思想描述如下:
如图2所示,对于航空集群机载网络,若将集群成员及其间通信链路分别对应节点集合V和边的集合E,则航空集群机载网络可以用图G(V,E)表示。记图G中节点数目|V|=n,边的数目|E|=m。以航空集群机载网络中各节点为圆心、节点最大通信距离r为半径作圆,若两个节点vi、vj间存在可行通信链路,则以两节点为端点的边e存在。将边e的权值定义为两个端点间的通信距离x,据此抽象出航空集群机载网络对应赋权连通图G(V,E)。

图2 网络模型Fig.2 Network model
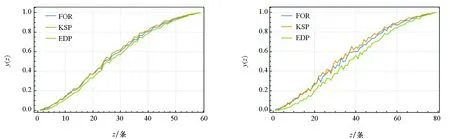
FOR路由策略旨在为航空集群机载网络拓扑图G(V,E)中每个源-目的节点对(s,t)规划k条(k>1且k∈Z+)可行路由pi。记节点对(s,t)之间所有可行路由{p1,p2,p3,…,pk}构成路由集合Ps,t。假设Ps,t中每条路由的失效概率均为q(0 S=(1-qk)×100% (1) 显然,当路由数量k增加时,通信成功概率S也将增大,通信可靠性随之提高。 现假设每条路由平均失效概率q=0.5,若要求节点对间通信成功概率S>90%,由式(1)计算知,需k≥4。因此,当输出路由数量取k=4时,理论上可保证平台间平均通信成功率在90%以上。 以图3所示节点对(s,t)为例,路由策略为该节点对之间规划的路由集合Ps,t,共含4条可行路由。值得注意的是,上述通信成功率的理论推导建立在各条路由失效为相互独立事件的基础上,若想实现通信成功概率在90%以上的可靠通信,路由策略需为节点对(s,t)间规划出互不相交的4条路由。然而,可靠性与实时性之间存在矛盾,严格不相交的约束将不可避免地增加路由长度,因此不相交路由策略可靠性的实现是以牺牲实时性为代价换取的,并不适合应用于对实时性、可靠性要求均较高的航空集群机载网络中。为兼顾通信实时性、可靠性,不妨将“严格”不相交的约束去掉,寻找长度较短且尽可能不相交的多样化路由。 图3 k=4路由策略示例Fig.3 An example of k=4 routing strategy 依据2.1节所述基本思想,设计一种满足航空集群机载网络高实时性、高可靠性要求的路由策略——FOR路由策略。该策略算法实现分为三个阶段: 阶段1:采用FRT算法,将高维度的航空集群机载网络拓扑图G(V,E)嵌入低维度的树形度量空间中,并使用树形图TG(Vt,Et)反映各节点间距离关系以及图上最短路由等特征。 阶段2:构建G(V,E)与TG(Vt,Et)的路由映射,据此为待通信节点对生成一条随机路由。 阶段3:多次重复阶段1、阶段2,得到多条随机路由,从中筛选出相对最优的k条路由。 2.2.1 FRT图嵌入 由于航空集群机载网络规模较大,其拓扑图属于复杂的高维空间,给路由的计算带来困难。通过FRT图嵌入算法,利用更为“简单”的低维树形度量空间近似表示高维网络拓扑空间,并使用树形图TG(Vt,Et)反映图G各节点间距离关系以及图上最短路由等特征,有助于快速存储、计算路由。 定义1用有序对(V,d)表示图G中两点i,j间图上距离(最短路由长度)形成的度量空间,其中d:V×V→R+,满足 1)∀i∈V,d(i,i)=0; 2)∀i,j∈V,d(i,j)=d(j,i); 3)∀i,j,k∈V,d(i,j)≤d(i,k)+d(k,j)(三角不等式); 4)当i≠j时, ∀i,j∈V,d(i,j)>0。 定义2若一个度量空间可以用赋权树形图表示,则称度量空间(V,d)为树形空间。 定义3若存在映射f:V→V2使得以下公式恒成立,则称度量空间(V2,d2)是度量空间(V,d)的一个失真度为γ的嵌入。 (2) 能够将任意拓扑图以低失真度嵌入树形空间中的算法通常为NP难度。Fakcharoenphol等[32]提出一种近似算法,即FRT图嵌入算法。FRT算法利用随机性,能够将任意一个含有n个节点的网络拓扑空间G(V,d)嵌入平均失真度为O(log2n)的一簇树形空间T(Vt,dt)中。 图4展示了采用FRT图嵌入算法将图G(V,d)随机嵌入树形空间T(Vt,dt) 的一个示例。值得注意的是,FRT算法设计之初并非针对路由问题而设,其在对点集V进行层次聚类时是基于空间距离关系,并未关注各点间实际路由连通性关系。因此,FRT算法并不能直接应用于航空集群机载网络路由策略中。为此,对原算法进行调整,使之拓展至图上最短路由长度所张成的度量空间上。调整后的FRT算法用伪代码描述,如算法1所示。 图4 FRT图嵌入Fig.4 FRT graph embedding 算法1 调整后的FRT算法 图5给出了算法1的一个运行结果示例。进一步分析知,输出树形图T根节点代表图G节点全集{V},叶子节点与单元素子集{vi}存在一一对应关系。逐层迭代嵌入实质上是将图G中节点依据两点间图上最短路由长度进行层次聚类,且总是以父节点对应节点集合中编号最小的点为聚类中心,下一层聚类半径最大值为上一层半径的1/2,各层最大半径依次为{2δ,U2δ-2,…,U20},因此位于第i层同一节点集合中任意两点间图上最短路由长度不会超过2i。考虑通信实时性要求,由点u到点v的路由应从同时包含u、v两点的最小公共祖先(Least Common Ancestor, LCA)对应节点集合中选取。 图5 算法1运行示例Fig.5 An example of Algorithm 1 2.2.2 路由映射 在阶段1求得树形图T的基础上,为确定任意两点间的实际路由,需进行路由映射,即:通过构建树形图TG(Vt,Et)与图G(V,E)中实际路由的映射关系,据此指导待通信节点对(s,t)间路由生成。为避免传统Oblivious路由策略采用随机算法进行路由映射所导致的路由不连通、代价不可控等问题,FOR路由策略中采用确定性路由映射,具体步骤如下: 步骤1:点的映射mV。Vt→V将树形图TG节点vt映射到图G中相应节点vi。映射mV(vt)结果为vt所表示点集中编号最小的节点(即该集合的聚类中心节点)对应原图G中相应节点。注意:经过FRT图嵌入后图G节点编号被打乱重排,进行映射时应还原节点自身编号。图6给出了点的映射示例。 图6 点的映射示例Fig.6 An example of node mapping 步骤2:构造路由生成树RT。经过步骤1点的映射后,将映射结果相同的点合并为一个点,即若mV(vt)=mV(ut)=vi,则将vt、ut合并,记作点vi,得到路由生成树RT。图7给出了路由生成树构造示例。 图7 路由生成树构造示例Fig.7 An example of routing tree construction 步骤3:边的映射mE。Ert→E*将树形图RT的边ert(vi,vj)映射到图G中对应的路由。定义映射mE(ert)结果为该边两个端节点在图G中的最短路由,并用最短路由所经过边的序列E*表示。图8给出了边的映射示例。 图8 边的映射示例Fig.8 An example of edge mapping 步骤4:确定路由。根据路由生成树RT,确定源节点s到目的节点t在图G中的路由。首先找到节点s、t在树形图RT中对应的路径,然后将该路径经过边的序列Ert按照mE映射到图G中的相应路由,最后删去路由中的冗余环路部分,输出源节点s到目的节点t的路由。图9给出了确定路由的一个示例。 图9 确定路由示例Fig.9 An example of route ascertainment 根据上述步骤,可为图G中任意两点确定一条无环路的连通路由。 2.2.3 筛选优质路由 对于阶段1输出的每个树形图TG,经阶段2路由映射可得一例路由生成树RT,从而据此确定图G中任意两点间路由。事实上,由于算法1中随机置换序列π和随机数U的不同会导致输出树形图TG不同,对应路由生成树RT也不同。通过多次循环阶段1、阶段2,得到多例不尽相同的RT,形成一簇RTs,据此为航空集群机载网络各节点对间筛选出长度较短且尽量不相交的k条优质路由。 假设由RTs为航空集群机载网络中节点对(s,t)规划出k′条不同的路由(k′>k),按路由长度由小到大依次排列,形成{p′1,p′2,p′3,…,p′k′},记作路由集合P′s,t。然后根据下述方程从中筛选出k条优质路由: MinimizeEdge_num{p1∩p2∩p3∩…∩pk} s.t.p1,p2,p3,…,pk∈P′s,t 其中,MinimizeEdge_num{p1∩p2∩p3∩…∩pk}表示在满足约束条件s.t.p1,p2,p3,…,pk∈P′s,t时,使得k条路由相交链路数目这一目标函数最小化。这样,由上述方程可确定k条长度较短且尽量不相交的路由,构成节点对(s,t)的路由集合Ps,t={p1,p2,p3,…,pk}。 基于以上对航空集群机载网络路由策略基本思想和算法步骤的阐述,FOR路由策略与经典Oblivious路由策略相比,创新之处在于: 1)经典Oblivious路由策略中,各边权重表示链路带宽,以实现负载均衡性能;FOR策略中,各边权重反映节点间通信距离,旨在保证通信时效性。 2)经典Oblivious路由策略采用随机算法进行路由映射,会导致生成路由不连通且路由长度不可控;FOR路由策略根据树形图所对应最短路由进行确定性路由映射,以减少迂回路由并确保路由的连通性。 3)经典Oblivious路由策略中,生成路由即被固定,不够灵活;FOR路由策略增设优质路由筛选机制,可根据实际需求调整输出路由,能够适应复杂多变的战场环境,具有较强的灵活性、可扩展性。 此外,尽管FOR路由策略具有一定的随机性,导致为航空集群机载网络各节点对(s,t)间规划的路由不一定为图上最短路由,但可以证明,该路由策略时效性代价是存在上界的。 对于航空集群机载网络,端到端时延反映其通信时效性,包括处理时延、排队时延、传输时延和传播时延等。其中,传播时延是指信息在飞机间的无线空间信道上传播所需的时间,与路由长度成正比。基于此,定量分析路由策略对传播时延的影响,以此衡量航空集群机载网络FOR路由策略的时效性。 3.1.1 概率分析 事实上,由于FOR路由策略在选取聚类中心节点时具有随机性,网络拓扑图G中任意节点都有可能出现在节点对(s,t)所对应的随机路由中。现通过概率分析证明,对于航空集群机载网络中节点对(s,t)之间的通信路由,距离两个节点较近的节点更容易出现在FOR路由策略的随机路由中。 定理1长度较长的路由出现的概率低于长度较短的路由。 证明:任取图G中两个节点a、b,设节点a、节点b与节点对(s,t)最短路由中点的距离分别为α、β(α<β)。现证明节点a具有更高的概率成为其最小共同祖先节点相应聚类中心节点。 若节点为节点对(s,t)最小共同祖先节点相应聚类中心节点,则聚类半径需恰好使得节点对(s,t)两个端点分离。如图10所示,图中红色区域表示图G中节点对(s,t)间最短路由长度为τ,则以聚类中心节点为端点,长度为聚类半径的线段的另一端点应落在红色区域内。 图10 聚类中心节点条件分析Fig.10 Analysis of clustering center node condition 算法1中聚类半径受到随机数U的影响。如图11所示,由于随机数U在区间[1,2)内等概率选取,当距离为d的节点向目标节点对(s,t) 瞄准时,线段的另一端点将均匀且随机地分布于区间[d,2d)内。故落在红色区域内的概率为: (3) 图11 随机数的影响分析Fig.11 Analysis of influence of random number 考虑任意两个节点a、b,有: (4) 由于α<β,故有Pa>Pb。因此,距离较近的节点具有更高的概率出现在两个通信节点所对应的随机路由中。 □ 3.1.2 竞争比分析 随着网络节点数目的增加,FOR路由策略生成随机路由长度具有较强的不确定性,从而影响该策略的时效性。为检验该路由策略的时效性,采用竞争比分析方法,以路由长度所引起的传播时延为影响因子,定量评估路由策略的时效性。 如图12所示,设基于最短路由算法生成的路由长度为l,依据FOR路由策略生成的k条路由平均长度为L,定义时延因子为: (5) 显然,总有l≤L,故γ≥1恒成立。由于输出路由具有随机性,考虑网络中任意两个节点间的路由长度,时延因子γ可视为一随机变量。整个网络中所有节点间路由时延因子的平均期望值E(γ)越小,即其值越接近于1,时效性越强。现计算路由策略时延因子γ的平均期望理论上界。 图12 时延因子示意Fig.12 Schematic diagram of delay factor 设网络拓扑图G中任意两点u、v间图上最短路由长度为dG(u,v),故: l=dG(u,v) (6) 设经图嵌入后,树形图上两点u、v间距离为dT(u、v)。则u,v两点间路由平均长度满足: L≤dT(u,v) (7) 因此,时延因子满足: (8) 由式(8)可计算时延因子上界值。 引理1在随机嵌入每一个树形图T的过程中, 图G中u、v两点嵌入dT(u,v)的聚类中心节点w存在且唯一。 证明:假设u、v两点之间随机嵌入的聚类中心节点w位于树形图的第iw层(iw≥2)。 1)存在性。节点对(u,v)与点w的距离关系如图13所示。由图13知,当且仅当dG(w,u)≤βiw (9) 图13 节点对(u,v)与点w距离关系图Fig.13 Distance between node w and node pair (u,v) 2)唯一性。假设存在两个不同层级聚类中心节点,这就意味着相邻两层节点集合完全相同,但相邻两层半径之差必定大于等于2,而图G中边长最小值为2,这显然是矛盾的。故缩小为原半径的1/2后必将产生新的集合,相邻两层节点集合不可能完全相同,点w唯一。 □ 引理2若生成节点对(u,v)之间路由的点w位于树形图中第i层,则必有dT(u,v)<2i+3。 证明:树形图中同时包含u、v两点的集合中层数最低的节点集合为最小共同祖先节点。如图14所示,假设同时包含u、v两点的最小共同祖先节点位于第i+1层,边(u,v)在树形图中所对应的路径,其实仅和u、v两点距离2i-1U以内的点有关。又因为1≤U<2,累加可得: (10) 图14 节点对(u,v)与第i层某点距离关系图Fig.14 Distance between node pair(u,v) and level i 基于上述引理,计算时延因子的平均期望值。值得注意的是,点w得以截断节点对(u,v)的前提是:点w的标号足够小,使得在其他距离节点对(u,v)较近的那些点之前率先掌握对于(u,v)的优先截断权。设比点w距离(u,v)更近的点共有s-1个,也就是说,按照与(u,v)图上距离从近到远排序,点w排在第s名。 则有: (11) 由三角不等式,dG(w,v)-dG(w,u)≤dG(u,v),因此: (12) 则期望值满足: (13) 右边分式约去公约数后,得: (14) 由调和级数展开式,得: (15) 知其与log2n同阶,故: (16) 对于任意节点数目为n的网络,时延因子平均上界存在,且理论期望为O(log2n)。 □ 综上所述,随着网络节点数目增加,时延因子并不是呈指数上升,而是呈对数级增长,这说明网络规模的增大并不会导致时延指数爆炸式增长。 为进一步论证FOR路由策略时效性,评估路由策略在不同规模网络下的实际效果,通过仿真实验研究该策略时延因子随网络规模增大的变化趋势,并在相同条件下进行时延因子变化对照实验,将FOR路由策略与KSP、EDP路由策略相比较。 实验在一台CPU为Intel Core i5、主频2.40 GHz、内存16 GB、64位操作系统的PC机上进行,算法编译采用科学计算软件Mathematica 12.0。利用Mathematica软件内置函数生成节点数目为3~100的网络,模拟不同规模的航空集群机载网络,并分别计算三种路由策略在不同规模网络中各节点对间路由时延因子平均值,绘制时延因子γ随网络节点数目n增大时的实际变化曲线,实验结果如图15所示。 图15 时延因子变化曲线图Fig.15 Delay factor curve 对比图15中三种路由策略在不同规模网络下的实验结果,可知: 1) 从变化趋势来看,随着节点数目n的增加,FOR路由策略时延因子缓慢增大,但增长速率逐渐趋缓,呈现对数级增长趋势,这说明网络规模的增大不会引发FOR路由策略时延因子呈指数爆炸性增长,这与3.1.2节中时延因子理论变化趋势相符;KSP路由策略时延因子的变化速率近似等于0,这说明KSP路由策略受网络规模增大影响不大;EDP路由策略的时延因子则随网络规模增大无明显变化规律。 2) 从波动幅度来看,本实验中FOR路由策略时延因子的最大值小于2,波动范围较小;KSP路由策略时延因子波动幅度并不大,基本维持在γ=1.25这一水平线上;而形成鲜明对比的是,EDP路由策略时延因子最大值超过3,随网络节点数目的改变有较大幅度的波动。 3) 对于同样规模的网络,当网络节点数目较小时,FOR路由策略时延因子大小与KSP路由策略较为接近;当网络节点数目较大时,FOR路由策略与EDP路由策略较为接近。因此可以推断,FOR路由策略的时效性能介于KSP路由策略与EDP路由策略之间。 4)本实验中时延因子最小值γ=1由FOR路由策略取得,这是因为存在一定的概率使得FOR路由策略生成的随机路由恰好与最短路由相同;KSP路由策略选取节点对间前K条最短路由,这K条不同的路由中必然存在非最短路由,故KSP路由策略时延因子恒大于1;图中EDP路由策略时延因子存在最低下限,则是由于其严格不相交的约束条件所导致的。 综上所述,尽管FOR路由策略的时效性略差于KSP路由策略,但显著优于EDP路由策略,且时延因子随网络规模的增大不会呈爆炸性增长,而是呈对数级缓慢增长,故FOR路由策略所引起的传播时延代价上界可控。 对于航空集群机载网络,一般情况下节点失效概率远小于链路失效概率。当航空集群机载网络编队拓扑随作战任务改变、通信连通状态变化或通信链路质量波动时,均可能导致其链路失效,从而引发路由失效。由于航空集群机载网络面临诸多不确定性因素,链路失效在整个网络中分布将呈现随机性。 若将链路随机失效视为路由策略进行路由选择的对手,为保证航空集群成员间通信可靠性,路由策略在进行路由选择时需与之展开一场博弈。在这场博弈中,路由策略应尽可能降低所选路由集合Pu,v中各路由失效风险,以提高路由策略鲁棒性,从而保障待通信节点对间通信可靠性。 现定义路由失效函数y(z)定量评估路由策略鲁棒性。对于边数为m的网络,该函数定义域为{z|0≤z≤m}。函数值y(z)表示随机删除网络拓扑中的z条边后,对应路由失效比例,即: (17) 式中,R表示路由策略为网络中所有待通信节点对(u,v)规划的路由集合Pu,v总数,r表示所有待通信节点对间失效路由集合Pu,v的数目。故函数值y(z)反映z条链路随机失效后,因路由失效导致节点对间通信中断数占所有待通信节点对数量的百分比。该比例越高,则整个网络中节点对之间通信连通率越低,通信可靠性越差。从理论上讲,函数值y(z)将随自变量z的增加而呈增长趋势。 对于任意给定的网络拓扑图G(V,E),在相同通信流量需求下,通过分别绘制采用不同路由策略时路由失效函数y(z) 实际曲线,比较相同z值时函数值大小,可评估路由策略的鲁棒性。若路由策略A对应曲线图像恒位于路由策略B所对应曲线下方,则路由策略A相较于路由策略B鲁棒性更强。 特别地,由于EDP路由策略能够为各节点对间规划出完全不相交的多条路由,失效概率最低,故理论上EDP路由策略鲁棒性最高,可将EDP路由失效曲线作为下界参考曲线,其他路由策略对应路由失效曲线应恒位于该参考曲线上方。一般而言,路由策略所对应路由失效曲线与EDP路由失效曲线越接近,鲁棒性越强。 为进一步论证航空集群机载网络FOR路由策略保障节点对间通信可靠性,评估其应对路由随机失效能力,通过仿真实验研究该策略的鲁棒性。实验中,采用Barabasi-Albert网络模拟航空集群机载网络复杂网络特征[41],通过随机删除网络拓扑图中的通信链路,模拟航空集群机载网络链路随机失效的不确定性,并进行100次重复实验,统计路由失效函数值y(z)的平均值,绘制其随失效链路数目增加变化曲线,并在相同条件下与KSP路由策略、EDP路由策略变化曲线相比较,检验FOR路由策略的可靠性。实验设定三种多路径路由算法为各节点对间规划路由数量k=|Pu,v|=2,结果如图16所示。 (a) n=11、m=19 (b) n=21、m=39 (c) n=31、m=59 (d) n=41、m=79 (e) n=51、m=99 (f) n=61、m=119 (g) n=71、m=139 (h) n=81、m=159 (i) n=91、m=179 (j) n=101、m=199图16 不同规模网络下三种路由策略仿真曲线Fig.16 Simulation curves of three routing strategy in different network scales 观察图16中不同规模网络下各路由策略仿真曲线,可得出以下结论: 1)随着删除边数的增加,三种路由策略的路由失效比例大致呈线性增长趋势,与4.1节中对路由失效函数y(z)的理论分析趋势相符。 2)当随机删除边数大于网络中总边数的50%时,FOR路由策略路由失效函数仿真曲线向EDP路由策略靠拢,此时FOR路由策略能够达到可与EDP路由策略相比拟的鲁棒性能,这说明FOR路由策略特别适合应用于易出现链路大规模失效的航空集群机载网络中。 3)尽管FOR路由策略的仿真曲线有时位于KSP路由策略曲线之上,但在大多数情况下,相比KSP路由策略,FOR路由策略具有更低的路由失效概率,反映出FOR路由策略应对链路故障鲁棒性强于KSP路由策略。 4)各仿真图中,EDP路由策略对应路由失效曲线恒位于其余两种路由策略对应路由失效曲线下方,这与理论预计结果相符,同时也验证了实验所得数据的真实性和可信度。 综上所述,与传统最短路由策略相比,FOR路由策略能够有效降低路由失效风险,提升航空集群机载网络路由鲁棒性;与EDP路由策略相比,FOR路由策略并没有通过刻意规避链路相交来提升鲁棒性,而是利用随机算法,巧妙地减少了各路由间的链路交叉概率。 针对航空集群机载网络路由失效问题,考虑到航空集群机载网络具有较强不确定性,提出一种可满足集群成员间信息传输实时性与可靠性需求的FOR路由策略。通过概率分析、竞争比分析等理论推导,以及时效性、鲁棒性仿真检验,结果表明:该策略能够有效降低航空集群机载网络路由失效风险,且时延代价上界存在,在航空集群机载网络中具有一定应用价值。此外,应该指出的是,由于FOR路由策略建立在随机算法的基础上,性能不太稳定,仍存在进一步改进空间。
2.2 算法实现








2.3 主要创新
3 路由策略时效性分析
3.1 理论分析






3.2 仿真分析

4 路由策略鲁棒性分析
4.1 理论分析
4.2 仿真分析




5 结论

