微通道内气泡和液滴自组织行为的研究进展

张志伟，朱春英，马友光，付涛涛

（天津大学化工学院，化学工程联合国家重点实验室，天津 300072）

引 言

有序的自组织现象受到人们长期的关注[1-7]，此种现象涉及自然界内多个领域，如果得到利用，将会为工程问题提供新的解决方案[8]。从21 世纪开始，微流体装置为在不同几何限制条件下受控产生液滴或气泡提供了一种强大的工具[9-18]。微流体中的两相流为非平衡系统的自组织现象或“耗散结构”的研究提供了一个简单的平台。在这个系统中，多相流相间相互作用导致了有序的自组织行为的出现[19-23]。乳剂、气泡和胶体长期以来一直被用作晶体模型，用于研究晶体界面、位错、塑性、其他材料科学和固体力学的核心过程[24-25]，而具有高体积分数的单分散乳化液滴形成的晶体相可以作为可调节的光蚀刻掩膜[26]。到目前为止，大多数研究工作都集中在简单通道几何形状的稀释乳剂或泡沫上。

近年来，微流控技术迅猛发展，各种构型的微流体装置都具备生产高度有序乳剂的能力，生成的液滴群或气泡群为高度有序、均匀排列的晶体结构的流动集合[26-31]。这种颗粒群的演化行为最初定义为泡沫自组织行为，这种行为取决于颗粒的制备和流体流动特性，既是微流体多相流研究的一个分支，也是微流体与多相流研究的一个应用方向。通过自组织行为演化得到的具有几何排列特征的气泡群或液滴群，为软流动晶体（soft flowing crystals，SFCs）[32-34]，是气泡群或液滴群自组织行为结果的体现。软流动晶体除了作为一种特殊的复杂流动物质的流动特征外，还有许多潜在的应用，如支架结构的组织过程或高度规则的催化多孔材料的组装过程[35-37]。国内外学者探索了微通道受限空间内气泡群的自组装行为及动力学反馈效应。研究发现，具有几何排列特点的微气泡或微液滴通过固化措施，可组装成新的固体超材料[38-39]，在声子晶体、光子学和过滤等领域具有潜在的应用价值。几种基于液滴的微流体芯片已成功地用于生产软流动晶体[40-43]。Fan 等[43]利用微流控技术的液滴自组织行为合成了多面水凝胶微粒，利用液滴在微流体装置中的自组织行为成功制备了三维排列的有序大孔膜。在此背景下，颗粒形态的规律性是表征软流动晶体的关键因素。本文主要针对液滴和气泡颗粒的自组织行为的研究进展进行综述，分析微通道构型和颗粒体积分数等变量对自组织行为的影响，为气泡或液滴自组织行为的进一步研究提供参考。

1 软流动晶体的流动特征

气泡和液滴在微流体装置内可以产生复杂的、有序的排列模式，因为它远离热力学平衡且连续运行[19]。微流体系统的流动通常很简单，低Reynolds数导致层流。气泡和液滴群的自组装模式取决于通道的几何形状和流体压力[20]，从而能够产生从单分散液滴到螺旋和条带的各种图案。两种具有流动界面的非均相流体的分散体系呈现出丰富的自组织结构。然而，单分散气泡或液滴微粒与纳米多孔材料的分子自组装不同，只能形成封闭的结构。因此，单分散气泡和液滴的自组装晶格结构的调控面临挑战，是研究的焦点。

1.1 自组织晶格形状

1933 年，Mann 等[44]的开创性工作中，描述了在压力作用下玻璃管内一系列油泡的显著规律性和稳定性。由此产生的图案被命名为“蜂窝”结构，它的特征是几何约束的函数，取决于管径。在接下来的几十年里，一些研究报道了各种泡沫的结构存在边界[45]。在传统的矩形微通道内，液滴群的自组织形状与通道构型相关[19]。利用液滴自组装行为可以控制三维晶格结构的有序大孔材料的合成，相较于传统的自上而下的图形化工艺，自组装工艺直接制作的3D多孔材料的成本降低。在矩形微通道内，当通道的尺寸远大于生成的气泡或液滴尺寸时，通道不限制气泡或液滴颗粒的运动，生成的气泡或液滴颗粒的自组织排列方式随着连续相体积分数的变化趋势相同。当微通道内液体体积分数大于0.12 时[46-47]，液体在气泡之间连续流动，称之为湿泡沫[48-49]。湿泡沫颗粒之间的挤压作用不明显，导致气泡为较为规整的球体形状，颗粒之间松散杂乱，呈现出无序的晶格排列方式，如图1(a)所示。当微通道内的液体体积分数接近于0 时，液体在气泡之间的流动较差，称之为干泡沫[50]。干泡沫颗粒之间的挤压作用明显，颗粒呈现出多边形的形状特征。与湿泡沫相异的是，干泡沫之间的排列方式呈现出无序和有序的晶格排列方式。有序的晶格排列方式出现在泡沫颗粒尺寸的均一性极好的条件下，气泡的相交边界的连线为规整的六边形[46]，三个气泡相交于一点，夹角为120°[51]，如图1(b)所示。无序排列的方式发生在气泡尺寸相差较大的情况下，此时，气泡的形状各异，多为不规整的多边形[51]，如图1(c)所示。

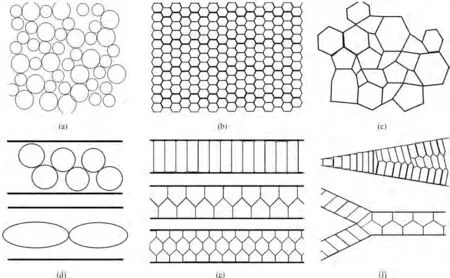
图1 湿泡沫中的无序晶格排列方式（a）；干泡沫中的有序晶格排列方式（b）；干泡沫中的无序晶格排列方式（c）；受限矩形微通道内的无序晶格排列方式（d）；受限矩形微通道内的有序晶格排列方式（e）；不规则受限微通道中的晶格排列方式（f）Fig.1 Disordered lattice arrangement in wet foam(a);Ordered lattice arrangement in dry foam(b);Disordered lattice arrangement in dry foam(c);Disordered lattice arrangement in restricted rectangular microchannels (d);Ordered lattice arrangement in restricted rectangular microchannels(e);Lattice arrangement in irregular restricted microchannels(f)

当气泡或液滴颗粒的收集通道的尺寸与生成的气泡或液滴尺寸相近时，通道会限制气泡或液滴颗粒的流动，生成的气泡或液滴颗粒的自组织排列方式会随着连续相体积分数的变化呈现相同的变化趋势。当微通道内的液体体积分数较大时，气泡之间的挤压作用不明显，但受通道尺寸的限制，气泡多会呈现出不规整的球体，此时气泡呈现出不紧密的单排和多排的排列方式[19]，如图1(d)所示。当微通道内的液相体积分数接近0 时，此时微通道内的气泡排列方式较为复杂。一般认为，变异系数小于或等于5%时，气泡的单分散性较好[28]，即均匀性好。当气泡的单分散性好，并且为单层的多行排列时，气泡为有序的六边形晶格排列方式[38]。当气泡的尺寸十分均一，并且为单层的两行排列时，气泡为有序的五边形排列方式，五边形的规整程度与气泡的流速相关[38,52]。当气泡的尺寸均一，并且为单层的单行排列时，气泡呈现出单层排列的不规整的四边形排列方式[38]，如图1(e)所示。然而，当气泡的尺寸差异较大时，气泡为无序的多边形晶格排列方式[35,53]，与上文所述的结果相类似。

在不规整的矩形微通道内，气泡和液滴颗粒的排列方式随着通道结构的变化而变化[54-55]。当微通道为高度不变的渐扩式矩形微通道时，随着微通道宽度的增大，气泡和液滴颗粒的排列方式会由单行转变为两行，进而转变为三行乃至多行[55]。其中单行（T1）排列方式依然为四边形晶格排列方式；两行（T2）排列方式为五边形晶格排列方式；三行（T3）排列方式为六边形和五边形同时存在的晶格排列方式，中间的气泡或液滴为六边形，靠近通道壁的两行气泡或液滴为五边形，如图1(f)所示。这种演变行为是可逆的，随着通道宽度的减小，颗粒的排列方式会呈现出逐行递减的趋势[55]。气泡或液滴在微通道内的自组织行为由自身尺寸和通道尺寸共同控制。分叉式微通道内的气泡或液滴排列方式的演化行为与渐扩式矩形微通道相类似，气泡或液滴由分支微通道汇入主通道时，泡沫颗粒由T1排列方式转变为T2 排列方式[55]，如图1(f)所示。在高度减小的渐进式矩形微通道内，圆盘或球缺式的气泡或液滴会沿平行于流动的方向拉长[38]，然后转变为六边形。这是由于在装置的限制下，气泡或液滴受到挤压变形将周围的连续相液体排开导致的结果。

1.2 周期性演化特征

张志伟等[56]发现，在受限微通道内，软流动晶格具有周期性演化特征。他们依据气泡群的几何排列特征，将气泡群划分为无序的三角晶格、有序的行三角晶格和有序的列三角晶格，如图2(a)所示。在恒定的操作条件下，三种排列的泡沫晶格会随着时间推移进行周期性的演化[13]，如图2(b)所示。这在泡沫流动中是一个意想不到的效应。Raven 等[57]也发现在一定操作条件下，气体流量和气泡体积都表现出较大的周期振荡，导致气泡会在微通道内由T1 晶格转变为T2 晶格，如图2(c)所示。通过在泡沫拓扑学和流变学之间建立联系解释泡沫晶格周期性变化的特征。气泡生成的驱动压力Pg与通道流动阻力和气泡流动速度v相关，气泡流动速度在恒定驱动压力下振荡，因此通道阻力也必须振荡。通道中泡沫流压力损耗的主要来源是通道壁与气泡之间的液膜滑动[58-59]，通道阻力与通道中泡沫薄膜的总长度成线性比例。因此，这种阻力取决于下游气泡的体积和泡沫的拓扑结构。

图2 泡沫晶格排列方式[56]（a）；泡沫晶格的排列方式的周期性演化图[13]（b）；周期性振荡泡沫发生器[57]（c）；复杂流动结构的排序[60]（d）Fig.2 Foam lattice arrangement[56](a)；The evolution of the arrangement of the foam lattice[13](b)；A periodically oscillating foam generator[57](c)；Ordering of the complex flow structures[60](d)

将新形成的气泡的大小与泡沫在通道中流动的阻力联系起来解释该现象，如式(1)[57]所示。

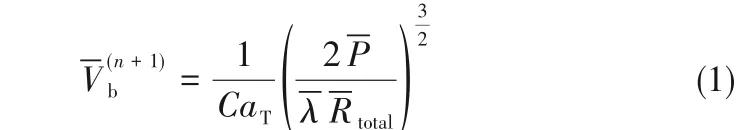
式中，-Vb为气泡的无量纲体积；CaT为泡沫流的毛细数；-P为通道的无量纲压降；-Rtotal为无量纲化的全部气泡的阻力值；-λ为数值常数。

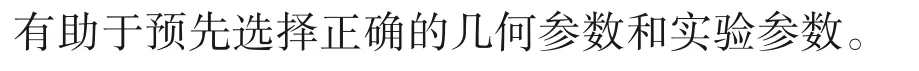
Raven 等[60]基于不同晶格结构的摩擦效应的差异，对这种周期性的自我调节机制进行了阐释，发现通道内的泡沫排列的晶格结构会影响总流阻Rtotal，如式(2)[60]所示。这个量将泡沫速度与施加的压力联系起来，如式（3）[60]所示。

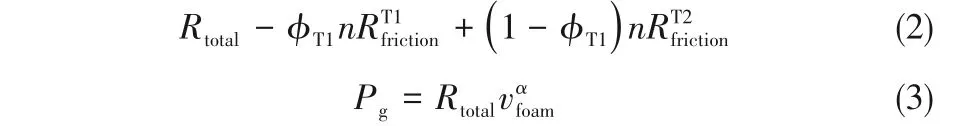
其中，φT1为微通道内T1 晶格的体积分数。可知，微通道内晶格的排列方式会影响微通道内的阻力大小。泡沫晶格的演化行为取决于气泡流动速度vfoam与T1 晶格的流动速度-vT1。如图2（d）所示，当气泡流动速度vfoam等于T1 晶格的流动速度-vT1时，通道内T1 晶格与T2 晶格共存；当vfoam>-vT1时，通道内气泡群为对流不稳定性流动；当vfoam<-vT1时，通道内泡沫晶格呈现出周期性演化的特征。

2 软流动晶体的自组装的影响因素

气泡群和液滴群的自组织行为和自组织结构特征变化趋势相似。研究表明，通道构型、气泡或液滴体积分数和颗粒尺寸都会影响液滴或气泡流动的晶格排布[54,61]。

2.1 气泡或液滴的体积分数

气泡或液滴颗粒的体积分数是自组织行为的重要影响因素。用气泡占据的通道底部面积的比例来近似计算气泡的体积分数φ。Garstecki 等[32]发现在φ值较低时，气泡无序地流动，在无界平面上气泡群的最大体积分数为φmax= π/(2 3 ) ≈0.91。当边界存在墙体时，最大值变小，其值取决于气泡有效尺寸与微通道宽度的比值（d/w）。当泡沫晶格处于φ=φmax的装填时，气泡保持圆盘形[32]。这些结构是由它们之间的弹性形状恢复作用决定的，同时是由于局部能量的最小值导致的。当φ≈1 时，气泡变得明显扭曲，界面动力学以惯性效应为主，典型的气液界面重排速度为ur=(γ/ρl)1/2，大约在1 m·s-1的量级，相关的时间尺度为l/ur约在100 μs，这两个值取决于通道的结构尺寸。系统的能量壁垒控制了结构弛豫的动力学，这一观察结果与一般认为泡沫结构的松弛是一个复杂而缓慢的过程[62]是一致的。

2.2 气泡或液滴的体积

张志伟等[56]发现当空腔内气泡群紧密排列时，气泡尺寸是决定气泡自组装路径的关键因素。如图3所示，气泡Ⅰ的尺寸大于其受力两侧的气泡，气泡的前端超出两侧气泡，使得气泡Ⅰ在气泡群挤压运动的过程中，前后两端受到不平衡的挤压力，后端的挤压力远大于前端的挤压力，气泡Ⅰ被挤出。当气泡受力两侧的气泡尺寸差异不大时，气泡呈现出有序的排列方式，即有序的行三角晶格、列三角晶格；当气泡与受力两侧的气泡尺寸差别较大时，气泡受周边不平衡的挤压力，使其找寻能够与自身形成局部最小界面能的位置，即受力两侧气泡尺寸相近的位置。气泡在非平衡力作用下移动过程使其周围呈现出无序的三角晶格。Garstecki 等[32]发现不同晶格排列方式的界面能存在差异，T3 晶格的界面能最低，T2 排第十五，而T1 则排在第31 位，它的界面能最高[32]。在低流速下，以较低的界面能值为特征的结构，而在较高的流速下，系统产生的晶格通常对应于较高的能量。

图3 收集腔内气泡路径演化图[56]Fig.3 Bubble path in the collection cavity[56]

2.3 通道构型

多种构型的微通道装置都可以用于生产软流动晶体，例如T型、同轴型、流体聚焦型和台阶式等，如图4(a)所示。研究发现，液滴群的重组依赖于液滴在空间约束下通过弯曲时被迫移动的路径长度[54]。Surenjav 等[63]研究了受限凝胶乳状液中液滴流过微通道弯道时的重组现象。如果弯曲角足够大，液滴将改变它们与周围液滴的邻接关系。这里研究的弯曲通道是在两个直线通道以特定的角度β相遇时形成的，随着弯曲角β的增加，液滴的易位数也会增加，是由于不同液滴阵列流过微通道弯曲处的路径长度不同。当β=20°时，没有观察到液滴的移位；当β=60°时，内排液滴（白色）比外排液滴（黑色）多移动了一个位置；随着弯曲角β的增大，液滴移位的数量增加到两个或更多；而当β=140°时，液滴会停留在弯曲处，如图4(b)所示。液滴移位的数量可以通过考虑液滴通过弯道的不同路径长度来解释，且与流速无关[54,63]。液滴的移位数如式（4）所示。

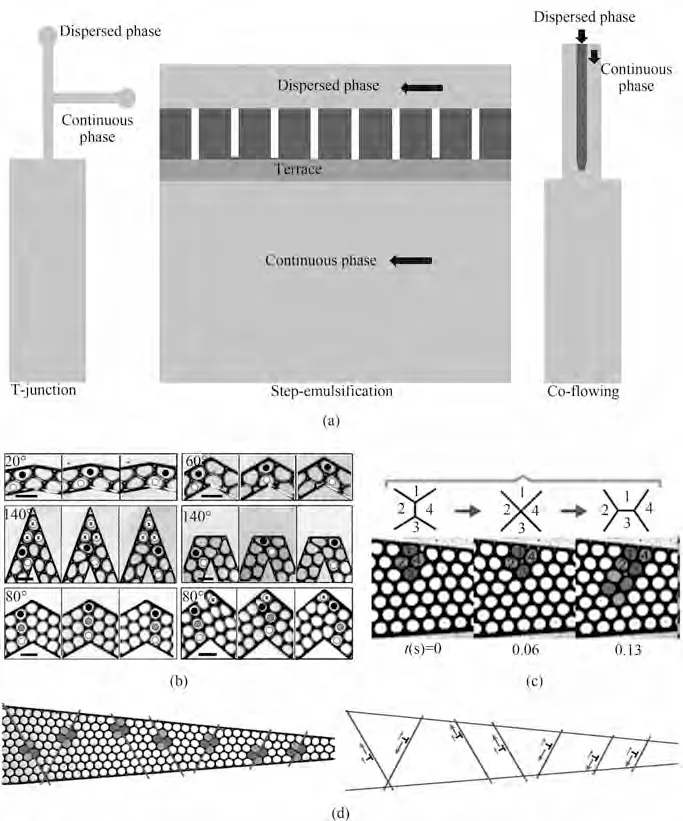
图4 用于生产软流动晶格的微装置构型图（a）；液滴排列沿弯角流动的时间序列[54]（b）；液滴群的重排过程[1]（c）；位错和滑移面在整个通道中的空间分布[1]（d）Fig.4 The configuration diagram of the microdevice used to produce the SFCs(a)；Time series of droplet arrangements flowing around angular bends[54](b)；The rearrangement process of the droplet swarm[1](c)；Spatial distribution of dislocations and slip planes throughout the channel[1](d)

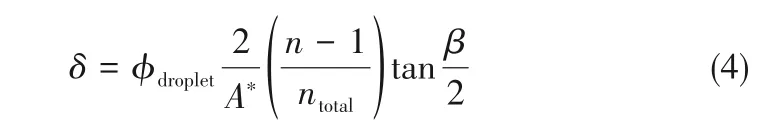
式中，ntotal为排列中的液滴行数；φdroplet为液滴的体积分数；A*=A/w2，为无量纲化的液滴的二维体积。

渐缩通道内存在液滴或气泡的重排现象[1]，如图4（c）、（d）所示，四个液滴之间的排列方式发生变化[64-65]，其中一个是发散的液滴（液滴2和4），另一个是会聚的液滴（液滴1 和3）[66]。从位错速度预测位错运动的时间周期T，考虑一个重排区域，其中液滴的行数从N减少到N-1。在稳态时，体积流量Q是恒定的，则

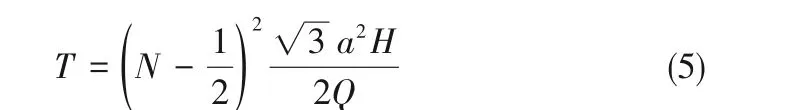
其中，H为通道宽度。

2.4 颗粒聚并效应的影响

气泡或液滴的聚并效应会导致大颗粒的生成，影响气泡或液滴的自组织行为[67-68]，如图5所示。在具有平滑横向边界的Hele Shaw单元中，单分散气泡在压力梯度作用下产生简单的塞状流[69]。相反，在多分散气泡的情况下，塞状流在临界速度阈值时经历一个急剧的动态转变，较大的气泡更快地通过泡沫，一旦充分发展，这种不稳定性会引起强烈的空间压力波动，导致薄膜破裂，对气泡的流动产生较大的影响，这种现象不能用准静态的观点来解释[70]。事实上，与剪切流不同的是，没有外部约束强制气泡重组，泡沫结构的变化本质上与耗散过程有关。大气泡产生较小的局部膜密度，因此，在介观尺度上的平均有效黏度较低。Cantat 等[69]在有序泡沫中嵌入单个大泡的情况下，得到大泡失稳阈值和大泡渐近速度相似的定律，流动速度的阈值表达式为

图5 大气泡周围的泡沫晶格排列Fig.5 Foam lattice arrangement around large bubbles

式中，D为大气泡的尺寸；vc为泡沫的临界流动速度；γ为气液界面张力；η为恒定的整体迁移率参数。

3 结 论

本文对非受限和受限空间内包含气泡和液滴的流动自组织行为的研究进行了综述，总结如下。

（1）气泡和液滴的自组织晶格存在两大类；有序的晶格和无序的晶格。其中有序的晶格多出现在分散相颗粒体积分数较大、颗粒尺寸均一和通道构型规整的条件下。在有序的晶格中也存在多种几何排列方式，如T1 晶格，为竹子节排列方式，T2为锯齿形排列方式。无序的晶格排列方式多发生在分散相颗粒体积分数较小、颗粒尺寸不均一和通道构型不规整的条件下。气泡或液滴的自组织行为在特定的条件下具有周期性演化的特征。

（2）通道构型、气泡或液滴体积分数、气泡或液滴尺寸、流动速度和聚并效应都会影响流动晶格的排布。不规整的通道构型会引发颗粒发生重排移位，体积分数会影响颗粒的流动状态，气泡或液滴尺寸的差异决定了自组织路径，气泡或液滴颗粒的流动速度会影响晶格的排列方式的转化，聚并效应会引起气泡或液滴晶格排列混乱。

气泡和液滴的自组织行为在三维复杂材料制备等领域具有巨大的应用前景，显然，要生产出优于传统自上而下装置的乳化自组装功能系统，还有很长的路要走。第一，高聚物材料的制备涉及非牛顿流体流动特性的研究，而非牛顿流体乳液的自组织行为未见报道，因此，非牛顿流体体系的自组织行为的研究是未来的重点研究方向。第二，气泡群和液滴群的自组织行为和自组织结构特征变化趋势相似，以往的研究中对于二者的区分不是特别清晰，但由于气泡与液滴在界面张力、密度和可压缩性方面的差异，这种物理性质的差异会影响两者自组织行为对于操控变量的灵敏程度，这不仅涉及长度尺度和时间尺度的问题，而且还有如何将许多不同的气泡或液滴含量、装置构型和物性参数共同耦合控制自组织行为的问题。因此，探究二者的异同点以及量化处理二者随操控变量的演化行为，将是下一步工作的研究重点。

符 号 说 明

A——泡沫表面积，m2

A*——无量纲化的气泡或液滴的二维尺寸

D——大气泡的尺寸，m

l——通道长度，m

n——气泡或液滴晶格的行数

P——压力，Pa

Q——流体的体积流量，m3•s-1

R——通道阻力，Pa·s·m-3

t——时间，s

u——流体流速，m·s-1

V——气泡或液滴体积，m3

v——气泡或液滴移动流速，m·s-1

w——通道宽度，m

α——幂律指数

β——通道弯曲角度，(°)

γ——气液表面张力，N•m-1

δ——液滴的移位数

η——恒定的整体迁移率参数

μ——流体剪切黏度，Pa•s

ρ——流体密度，kg·m-3

φ——气泡或液滴占微通道的体积分数

下角标

c——临界

droplet——液滴

foam——泡沫

g——气体

max——最大值

r——重排

total——全部