一类周期演化域上疟疾模型的动力学
宋小飞, 朱 敏, 刘梦丽
(安徽师范大学数学与统计学院, 安徽 芜湖 241000)
疟疾是由寄生虫引起的一种致命疾病, 通过受感染的雌性按蚊叮咬传播给人类.疟疾的传播取决于蚊虫的数量、蚊虫的叮咬率, 仅2017年全球就有约2.19亿疟疾病例和高达43.5万的死亡病例, 超过30亿美元用于控制和治疗疟疾[1], 这给世界的经济发展和公共医疗带来了沉重的负担, 因此研究疟疾的传播机制,预测它的变化具有重要意义.近些年, 运用数学模型研究传染病的特征逐渐受到人们的重视.Dembele等[2]在一维系统中引入周期系数, 给出了蚊虫出生率和死亡率的季节变化对疟疾传播的影响; Lou等[3]研究固定区域上非局部时滞反应扩散模型, 获得了保证疾病稳定在正稳态的充分条件; Safan等[4]根据疟疾的传播机制构建无量纲化后的常微分模型
其中Sh,Sv分别表示总人口中易感人群的比例和蚊虫种群中易感蚊虫的比例;Ih,Iv分别是总人口中已感人群的比例和蚊虫种群中已感蚊虫的比例;Cvh和Chv分别代表已感蚊虫传给易感人的比例和已感人传给易感蚊虫的比例;βh与βv分别是人口出生率和蚊虫的出生率;γh是感染状态下人的非自然死亡率;c表示人因病致死率, 故0≤c<1.针对模型(1), 作者假设Sh+Ih=1和Sv+Iv=1, 并将模型(1)简化为

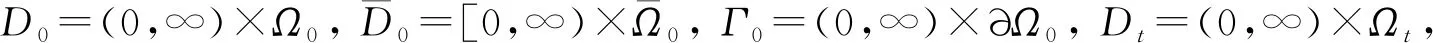
1 模型建立
对于任意的x(t)∈Ωt,Ih(t,x(t))和Iv(t,x(t))表示t时刻x(t)处被感染的人和蚊虫的比例[7].同时, 区域的变化会产生流速, 从而造成变量Ih和Iv产生对流项和稀释项, 其中对流项为a·Ih和a·Iv, 由质点以一定速度a在Ωt内移动产生, 且稀释项为Ih(·a)和Iv(·a), 由区域Ωt局部体积变化产生.因此, 根据质量守恒原理和Reynolds输运定理[8]将上述模型扩展为
(3)
并伴随Dirichlet边界条件
Ih(t,x(t))=Iv(t,x(t))=0,x(t)∈∂Ωt,
(4)
初始条件
(Ih(0,x),Iv(0,x))=(Ih,0,Iv,0)(x),x∈Ω0,
(5)
其中Ih,0(x)和Iv,0(x)是正的有界连续函数,dh(t,x)和dv(t,x)分别表示人和蚊虫的扩散系数, 并假设dh(t,x),dv(t,x),Cvh(t,x),Chv(t,x),βh(t,x),βv(t,x),γh(t,x)和c(t,x)都以T为周期非负且充分光滑的函数.
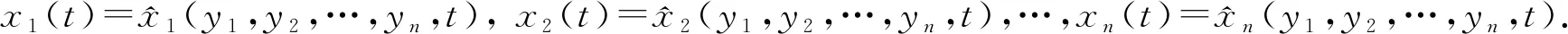
(6)
故演化区域Ωt上的问题(3)~(5)转化成固定区域Ω0上的问题(6).
2 基本再生数
基本再生数通常用来评估疾病传播的风险.对于反应扩散系统, 通常使用下一代感染算子的谱半径[10]以及相应的主特征值问题来分析基本再生数[11].
因(0,0)是方程(6)的无病平衡点, 故可将方程(6)在(0,0)点处线性化,得
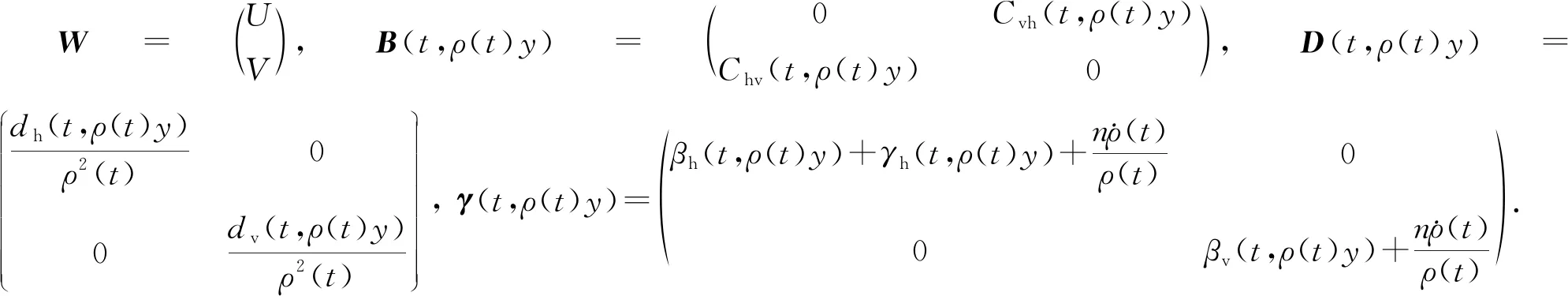

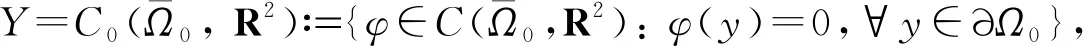
由文献[12]中定理2.7(ii)和文献[13]中定理3.7可得下面引理的两个结论.
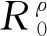
(7)
的主特征值, 其中(φ,ψ)∈CT×CT都是Ω0上正的特征函数对.

的主特征值, 其中(φ,ψ)如i)中定义.
定理2下列命题成立.
i) 问题(6)的基本再生数满足
ii) 如果g(t,ρ(t)y)=g(t)仅与t有关, 式中g≡Cvh,Chv,βh,βv,dh,dv,γh, 则
iii) 如果g(t,ρ(t)y)=g为常数, 这里g≡Cvh,Chv,βh,βv,dh,dv,γh, 则式(10)可简化为
iv) 在iii)的假设下, 若ρ(t)≡1,则有
其中μ*是特征值问题-Δφ=μ*φ,y∈Ω0,φ=0,y∈∂Ω0的主特征值.
证明 令
φ(t,y)=p(t)φ(y),ψ(t,y)=q(t)φ(y), (t,y)∈D0,
(13)
其中φ是定理2中的特征函数,p和q待定且满足
p(t)=p(t+T),q(t)=q(t+T),t>0.
(14)
将式(13), (14)代入式(7)得
利用p(t),q(t),ρ(t)关于t的周期性, 对此式积分, 并利用Hölder不等式易得
故式(9)成立.而命题ii)和iii)均为命题i)的特殊情况, 可由式(9)推出.对于命题iv), 可将问题(15)简化为
再通过求解此常微分方程组可得式(12).
3 区域的周期性演化对疟疾模型的动力学影响
系统(6)的稳定态为
(16)
其中G1(t,y,ρ(t),U,V),G2(t,y,ρ(t),U,V)分别为系统(6)中第一个方程和第二个方程的右端项.

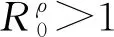
结合初值条件

(18)

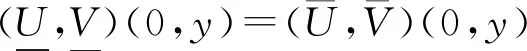
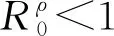

当c(t,ρ(t)y)≡0时, 采用反证法.事实上, 如果(U+,V+)(t,y)是系统(16)的正解,则有不等式
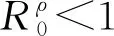
接下来, 根据文献[14]中定理3.1可直接获得周期解的稳定性.
定理4设(u,v)(t+kT,y;U0,V0)是问题(6)的任意一个解.
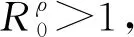
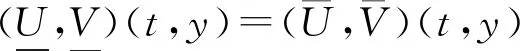
注:如果ρ(t)≡1, 则Ωt就是固定区域Ω0, 定理3和4相应地体现了固定区域Ω0上系统(6)的动力学结论.
4 数值模拟与生物学解释
传染病学参数取值为[4]:Cvh=0.64,Chv=0.27,βh=1.1×10-4,βv=0.13,γh=0.02,c=3.5×10-3; 扩散系数以及初始值取为:dh=0.02,dv=0.01,U0(y)=0.04cos(πy),V0(y)=0.09+0.06cos(πy), 并假定Ω0=(0,1), 则μ*=π2.选取以2π为周期的演化率ρ(t),ρ(t)在[0, 2π)中定义为
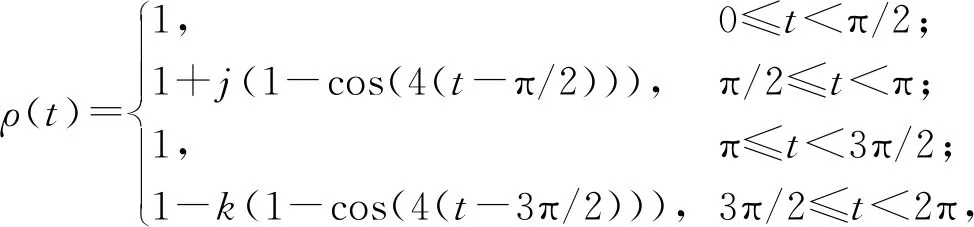
其中j∈(0,∞),k∈(0,1/2).选择不同的j和k进行数值模拟, 通过ρ(t)的变化观察人群中疟疾病例的变化趋势.
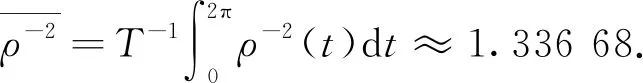

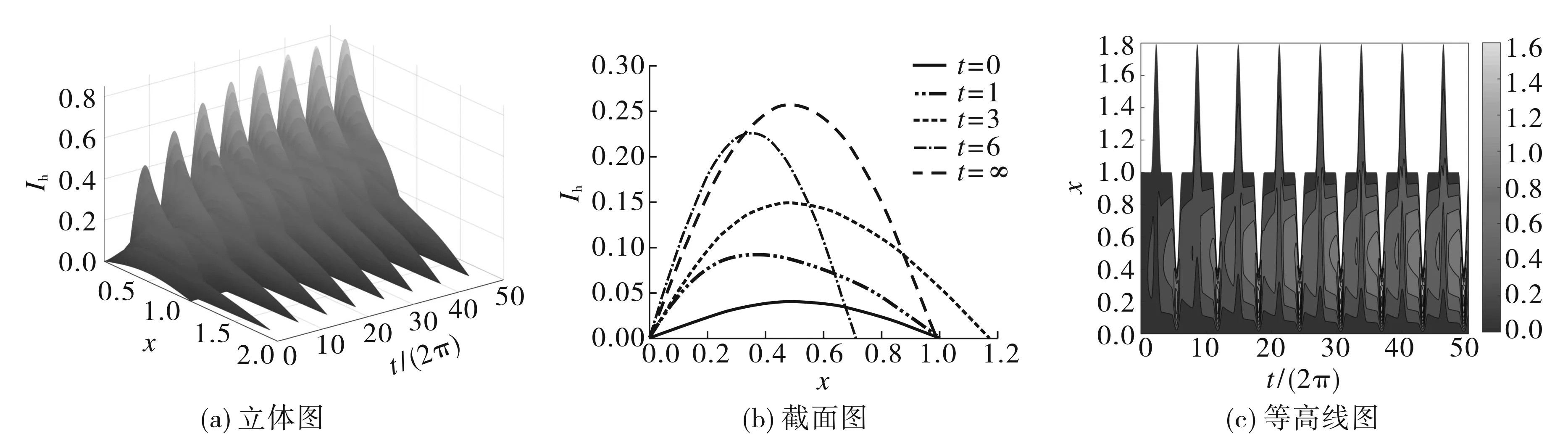
图时人群中疟疾病例的变化趋势

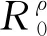

图变大时人群中疟疾病例的变化趋势
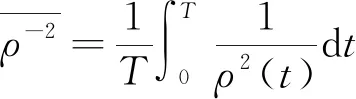
——“零疟疾从我开始”

