舰载武器系统目指精度预估模型研究

罗双喜

（江苏自动化研究所，江苏 连云港 222061）

0 引言

在舰载火炮/导弹武器系统中，目标指示（简称目指）是指利用来自本舰传感器的目标航迹数据，实时引导跟踪传感器对目标进行捕获跟踪的过程。目指精度决定了武器系统能否实现对目标的快速跟踪［1］，并直接影响到跟踪传感器捕获目标的反应时间这一关键性能指标，因而对武器系统至关重要。对于舰载武器系统，目指精度的实时预估结果则是战术决策的重要依据之一［2］。

跟踪传感器对目标的捕获跟踪过程，主要包括调舷与搜索捕获两个子过程，前者是将跟踪传感器的指向器向目标所在的方向进行调转，以便对准目标的过程，后者则是跟踪波束围绕目指提供的目标位置进行搜索捕获的过程。根据目指数据是二维或三维的不同而分为方位扇扫+俯仰搜索和圆（锥）扫描两种方式。通常情况下，扇扫的反应时间相对较长，但圆扫涉及的方位和俯仰范围更小，因而要求更高的目指精度。理论上，只要目标落入跟踪传感器波束有效搜索范围内（一般为波束宽度的2倍），跟踪器便能够快速捕获目标，在跟踪器进入稳定跟踪状态之前，要求目标指示数据实时更新并保持稳定输出。

搜索传感器输出的目标航迹，其数据更新周期大约在秒级，而跟踪传感器的信号/数据处理频率则为50/100 Hz 甚至更高。将航迹数据通过外推等技术方法转换为按跟踪器跟踪周期输出当前时刻的目标位置数据和（径向）速度数据的过程，称为目指加密（加细）。显然，目指加密输出的目标位置数据是外推结果。在应用中，航迹数据的产生时刻通常要比数据报文的接收时间略早，因而外推的时间间隔通常比搜索传感器的扫描周期更长一些。

另一方面，航迹数据的坐标原点与跟踪器的原点通常是不一致的，因而存在基线修正的问题。对于舰艇平台，基线参数是搜索传感器/跟踪传感器到作战系统指定的中心点的甲板坐标系参数，而目指数据则是舰载稳定坐标系的数据，因而需通过摇摆变换将基线参数转换为稳定坐标系下的参数。

综上所述，目指加密的数学模型可描述为

其中，Yn为tn时刻包含位置Xn、速度等信息的目标运动参数，t 为当前时刻，Δt=t-tn为预测时间，F（·，·）为预测函数（可以采用卡尔曼滤波中的状态转移函数），XB（t）为基线参数的摇摆变换结果：

其中，XS、XT分别是搜索传感器和跟踪传感器的基线参数（甲板坐标系），Θ（t）为摇摆变换矩阵。

目指精度参数主要包括目标距离、方位和径向速度的系统误差和均方根误差，在系统误差未知等情况下则用原点矩误差来表示。目标位置、速度和航向等其他精度参数则较少使用。

理论上，可以利用搜索传感器的滤波协方差矩阵来预估目指距离等参数的精度，但在实际应用中搜索传感器发送的航迹表数据不含误差信息，因而这种方法是不可行的。如何利用目标航迹数据对目指精度直接进行估计，是目指精度预估所面临的主要困难。国内外学者对目指精度的影响因素［3］、分析方法［4］等有所研究，但未见涉及目指精度预估的模型与算法研究。

本文首先建立目指精度参数的理论计算模型，然后结合最小二乘滤波（LSF）/加权最小二乘滤波（WLSF），导出相应目指距离精度、目指方位精度和径向速度精度的简化计算模型，并利用仿真航路数据进行了验证。为简便起见，将目标航迹局限于二维平面情形，此时基线修正只取摇摆变换后的x-y分量，或者采用简单的航向变换来代替摇摆变换，并认为导航参数与基线参数的测量误差可以忽略不计。

1 理论精度计算公式

假设搜索传感器的距离、方位测量精度分别为σr和σβ，测量方差为

其中，

相应卡尔曼滤波的状态方程与量测方程为：

其中，Φ（tn）和G（tn）为状态转移矩阵和状态噪声矩阵，其选取取决于所采用的目标运动模型。对于情报处理系统来说，大多采用匀速直线模型，相应的状态向量和状态转移矩阵为：

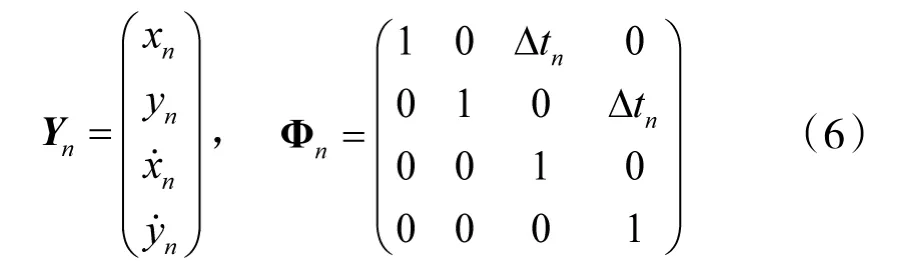
在工程应用中，一般都是利用转换后的直角坐标测量数据（伪量测）进行滤波，则量测方程为

在卡尔曼滤波方程（此处从略）中，通常用Pn/n和Pn+1/n分别表示滤波误差与预测误差的协方差矩阵。

根据Kalman 滤波理论，若将状态噪声的方差矩阵Qn作零处理，则Kalman 滤波就退化为最小二乘滤波。在雷达数据处理领域，更常用的是α-β 滤波和最小二乘滤波（包括滑窗、解耦等形式）。

在目标航迹的下一次数据更新之前，只能利用当前周期更新后的航迹数据进行外推，来获得当前时刻的目标位置数据（距离、方位），而径向速度则只能使用前一周期更新后的速度信息。通常情况下，目指的数据率与跟踪器的工作频率保持一致。

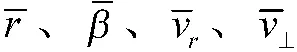
目指预测过程一般都是基于式（5）来进行的。在工程应用中，最常用的是基于匀速直线模型的外推方法，相应的目指预测协方差矩阵为：

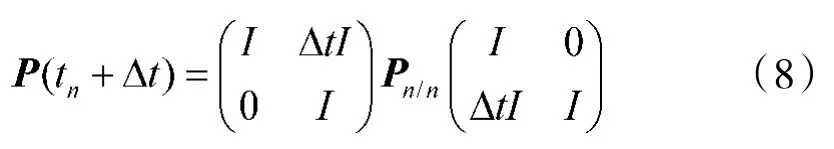
其中，Pn/n为滤波协方差矩阵。如果采用辛格等其他滤波模型，则Pn/n表示其滤波协方差矩阵中对应位置和速度的子矩阵。将滤波协方差与预测方差矩阵写成分块形式：

则有

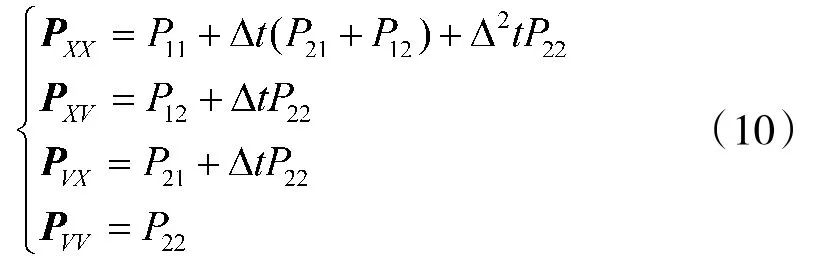
根据目指预测的协方差矩阵，即可得到目指距离精度等指标参数的理论计算公式。

1.1 目指距离精度

因为

求微分，得到

所以，在目指预测点处的目指距离误差方差为

1.2 目指方位精度

因为

求微分，得到

所以，在目指预测点处的目指方位误差方差为

1.3 目指径向速度精度

目标速度矢量可分解为径向速度和切向速度两个相互垂直的分量。目标航向与方位线的夹角θ通常称为攻击角，如图1 所示。

图1 目指径向速度分解示意图

径向速度的计算公式为

其中，C 为目标航向，v 为目标速度。

对（x，y）求偏导，得到

1.4 目标航向精度

因为

求微分，得到

因此，目标航向精度的计算公式为：

无论是一般形式的卡尔曼滤波还是最小二乘滤波，理论上均可根据式（13）、式（16）、式（20）和式（23）来计算目指精度参数，主要困难在于预测协方差矩阵或滤波协方差矩阵的获取，因为搜索传感器提供的目标航迹表并不包含这些数据。为避开这一困难，在下一节中，假设搜索传感器采用最小二乘滤波/最小二乘滤波，输出滤波更新后的目标航迹，在此假设基础上直接建立目指距离精度、目指方位精度等指标参数的计算公式，以避免直接使用滤波方差矩阵等数据。

2 简化计算模型

假设X 为目标位置（直角坐标）向量，V 为目标速度向量，T 为搜索雷达扫描周期，则n 个周期的加权最小二乘状态估计可描述为下述最小化问题：

其中，

上述形式的最小二乘滤波方法将二维平面的目标状态向量作为一个整体进行滤波，而不是解耦后分别在X、Y 方向上独立进行滤波。权系数矩阵Wi有多种选择，例如常系数矩阵W，或者测量误差方差矩阵Ri（见式（4））。

作为二次多项式，式（24）可改写为

滤波误差方差矩阵为：

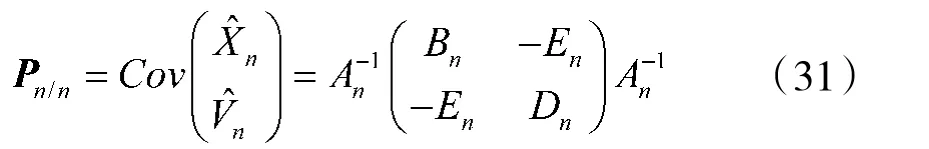
其中，

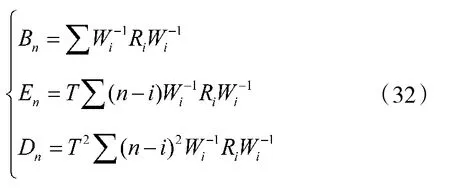
下面分别对Wi取常数矩阵W 的最小二乘滤波和测量误差方差矩阵Ri的加权最小二乘滤波两种典型情况，予以进一步的分析，导出更实用、简化的目指精度计算公式。

2.1 最小二乘滤波下的目指精度

当Wi取常数矩阵W 时，有

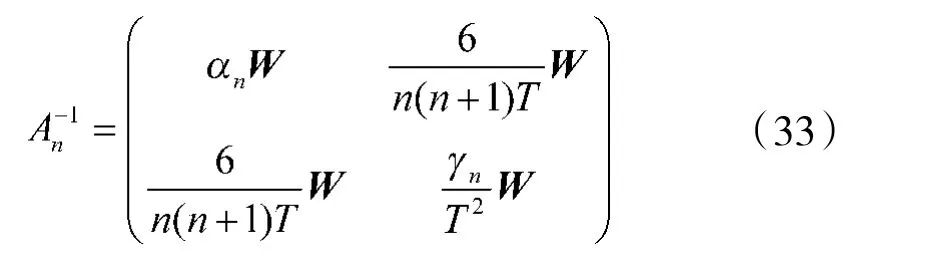
其中，

式（28）成为

其中，I2表示二阶单位矩阵。

滤波方差矩阵Pn/n满足：

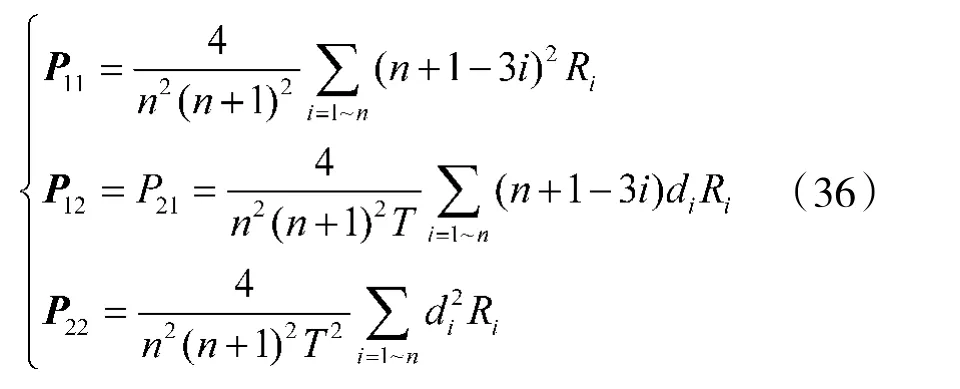
相应的，式（10）成为：

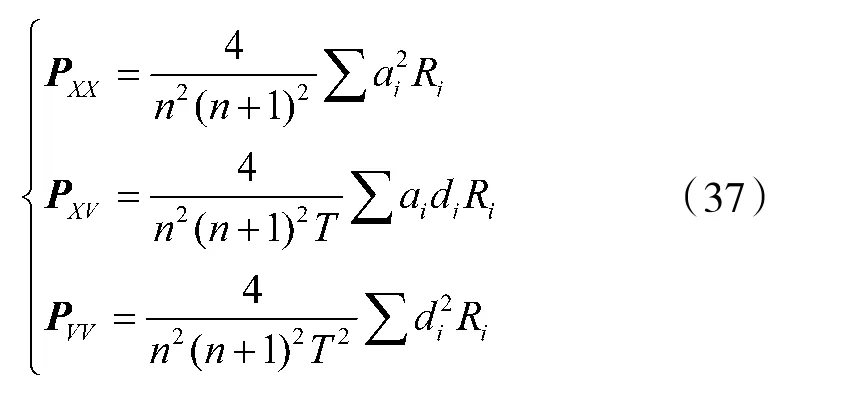
其中，

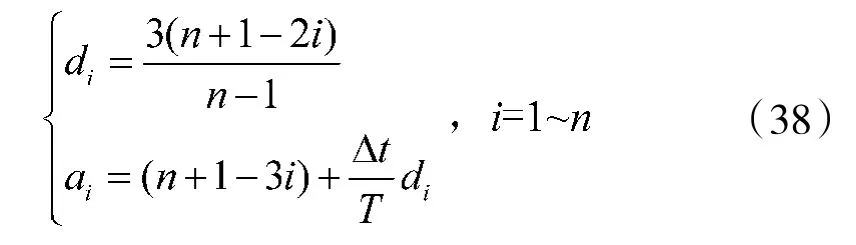
从式（35）～式（37）可以看出，滤波值、滤波方差及预测方差与权系数矩阵W 无关。

记

则有

另一方面，有

根据式（13）与式（16），有

从式（44）与式（45）可以看出：

对于径向速度与目标航向，经类似分析后可得到其精度计算公式：

其中，

若记

则可得到简化计算公式：

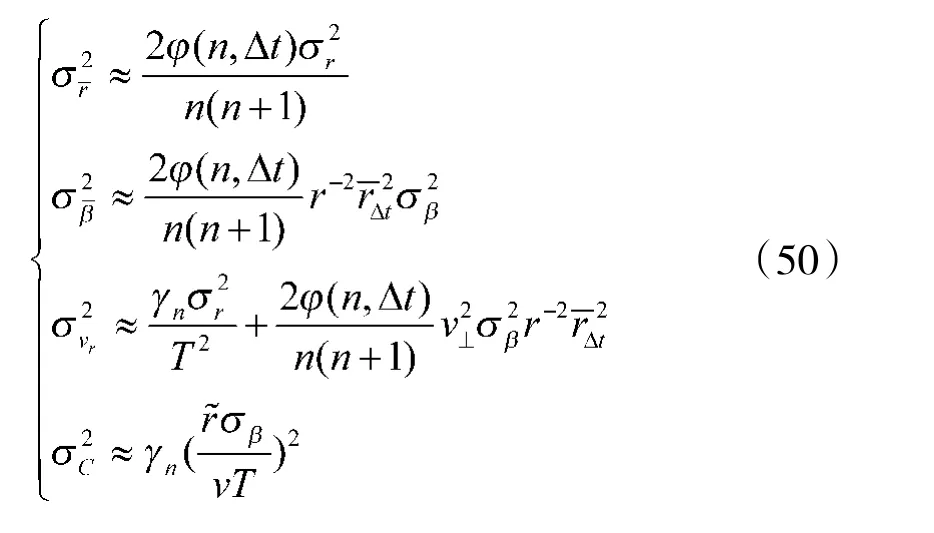
特别地，对于一步预测（Δt=T），有

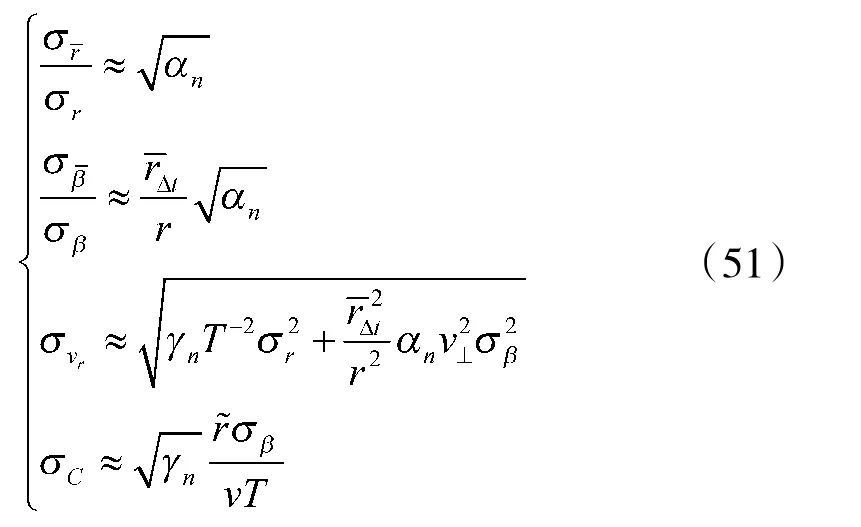
2.2 加权最小二乘滤波下的目指精度

当选取测量方差矩阵Ri的逆矩阵为权系数矩阵时，从式（31）、式（32）可知：

尽管诸测量方差矩阵Ri不尽相同，但An可改写为

其中，

则立即得到

特别地，对于一步预测（Δt=T），有

2.3 两种简化模型的比较分析与仿真验证

在上面两个小节中，分别针对LS 和WLS，导出了目指距离精度、目指方位精度、目指径向速度精度与目标航向精度的计算公式与相应的简化计算公式。根据这些公式，只需要知道n 的取值，或者根据搜索传感器性能和目标航迹的历史数据合理选取n，并用目标航迹的距离/方位值代替公式中的距离/方位测量值，即可实现目指精度参数的在线预估。

2.3.1 比较分析

对式（63）、式（64）与式（50）、式（51）进行比较，可得出以下结果：

1）目指距离精度

2）目指方位精度

对于两种最小二乘滤波，目指方位误差的方差计算公式基本相同，都是n 与两个距离量之比值的乘积，该比值的分母项都是预测点的距离，而分子项则可看作一种加权平均距离，差别仅仅在于加权平均距离的计算方法不同。对于临近本舰的目标，该比值一般大于1。

3）径向速度精度

两种滤波方式下，径向速度方差的计算公式基本相同，都是两部分的线性组合：一部分是切向速度、方位测量精度、距离量比值三者乘积的平方，另一部分是距离测量精度与扫描周期比值的平方。两者的差异在于第一部分中的加权平均距离计算公式不同。

从式（51）或式（64）来看，对于攻击本舰的临近目标，尽管加权距离与目指预测点距离的比值大于1，但第1 项的数值通常在两位数量级，第2 项的数值在个位数量级，因此，径向速度的精度主要取决于距离测量误差和n 的大小。以具体例子说明如下：假设目标速度1 000 m/s，雷达的距离、方位测量误差分别为30 m 和0.3°，初始攻击角为15°，则切向速度约为258.8 m/s，当n=6 时，有

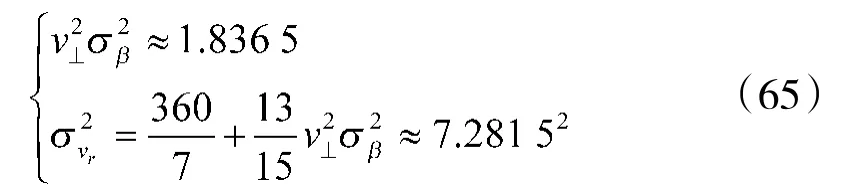
4）目标航向精度

航向精度的计算公式基本相同，均与方位测量精度与某种加权距离（或）的乘积与vT 的比值成正比，表示目标运动方向在该距离上相对于vT 的“摆动”幅度。差异在于加权距离的计算方法不同。

2.3.2 仿真验证

设定两条典型的匀速直线航路，其参数设置如表1 所示。二者的初始位置与速度相同，初始航向在航路的两侧（离轴角分别为10°与20°），传感器的距离与方位测量精度不同。

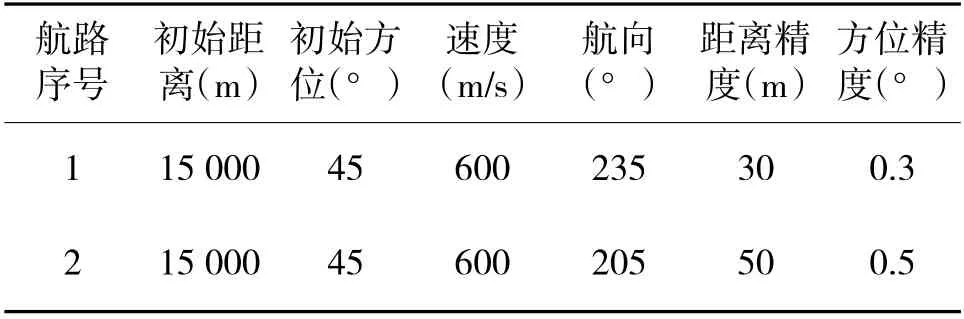
表1 仿真航路参数表

通常情况下，当指控系统发出目指时，目标距离本舰已较近，离轴角不会太大；选择相同的初始距离、方位和速度值，则便于LSF 和WSF 两种滤波模型下精度估计结果的比较。图2 ～图4 分别为航路1 的距离精度、方位精度和径向速度精度在LSF模型下的理论值与估计值曲线，图5 ～图7 则是航路1 在LSF 和WLSF 两种模型下的精度预估误差，图8 ～图10 则是航路2 在LSF 和WLSF 模型下的理论值与估计值。

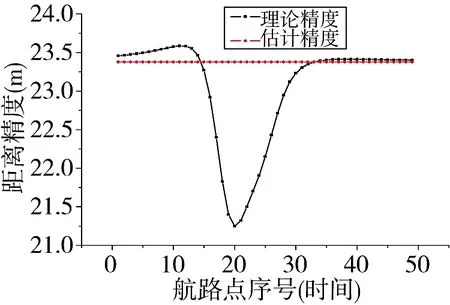
图2 距离精度（航路1，LSF）

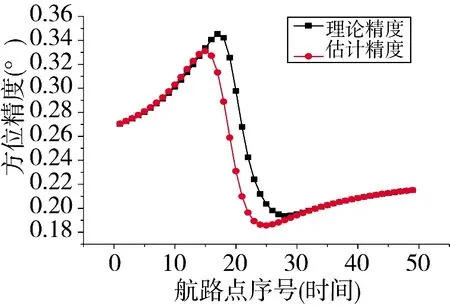
图3 方位精度（航路1，LSF）

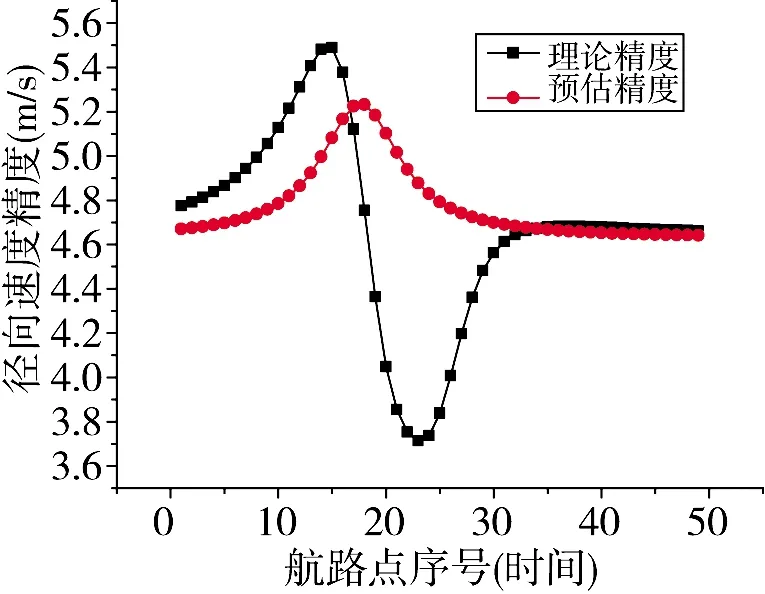
图4 径向速度精度（航路1，LSF）

图5 距离精度的估计误差（航路1）

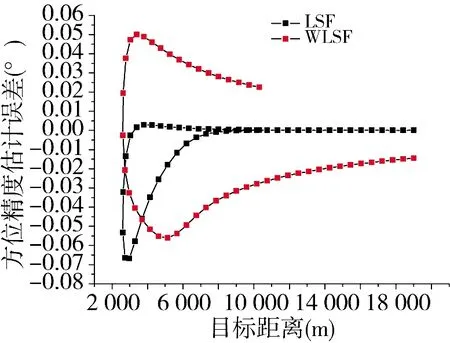
图6 方位精度的估计误差（航路1）

图7 径向速度精度的误差（航路1）

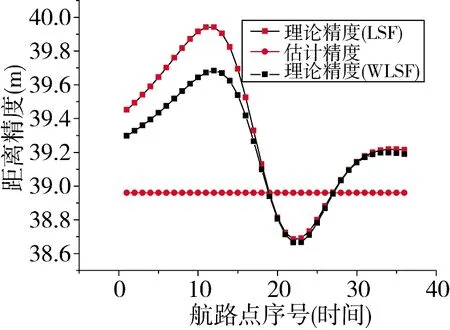
图8 距离精度（航路2）

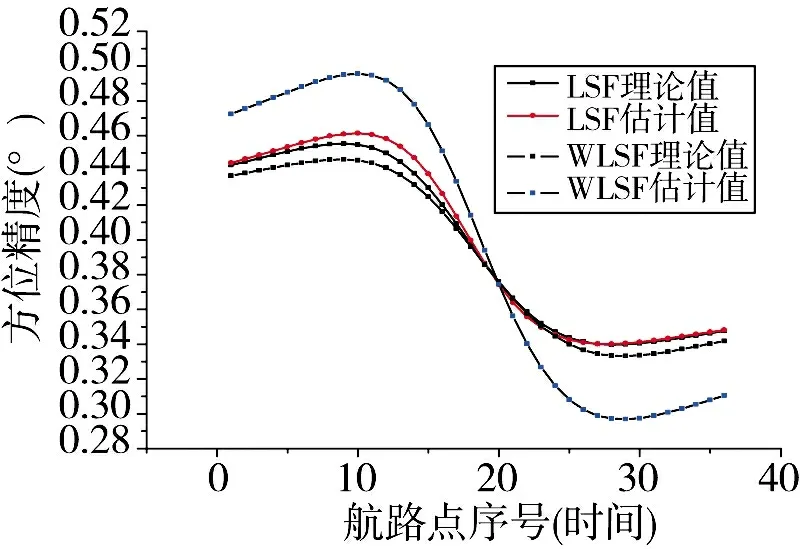
图9 方位精度（航路2）

图10 径向速度精度（航路2）

在这些图中，理论值是指根据理论式（13）、式（16）和式（20）计算的结果，估计值则是根据简化式（51）或式（64）的计算结果。计算过程所采用的航路点数据没有叠加随机噪声。

从上述两个航路的仿真数据结果来看，主要有以下几点结论：

1）对于距离精度、方位精度和径向速度精度这3 个精度参数，无论是采用LSF 或WLSF 滤波，相应简化模型的精度估计误差均较小，在合理范围内。

2）采用WLSF 的估计误差要比采用LSF 的估计误差要略大一些。

3）目标距离较远时，估计误差较小；目标距离较近时，估计误差明显增大，尤其在航路勾径点附近。

4）目标攻击角对精度参数估计的影响不是很显著。

3 结论

本文针对目指距离精度、目指方位精度和径向速度精度等主要目指精度参数的在线预估问题开展了分析，建立了简化的精度估计模型，并进行了仿真验证。上述简化模型是基于匀速直线运动模型的，理论上具有一定程度的局限性。从工程应用的角度来看，其理论分析过程与验证结果均表明，简化模型的计算公式物理含义直观、明确，估计误差在合理范围之内，能够为目指精度参数的在线预估提供模型和方法的支持，并为火炮/导弹武器系统目指精度指标的确定提供理论依据。