基于深度强化学习的NOMA系统功率分配

刘树培

(南京邮电大学通信与信息工程学院，江苏 南京 210003)

1 概述

非正交多址(NOMA:Non-orthogonal multiple access)是一种有着广泛应用前景的技术。NOMA的基本思想是让多个用户复用同一频带资源，主动引入干扰信息，在接收端使用串行干扰删除(SIC：Successive interference cancelation)实现正确解调。具有高容量、低延迟、支持大规模连接等技术特点。在对NOMA系统的研究中，资源分配问题是其中的重要一环。资源管理策略包括功率控制、信道分配、用户聚类、用户调度、速率控制等。通过适当的资源管理和利用功率域中的用户多样性，可以协调NOMA用户之间的干扰，从而提升NOMA网络的性能[1]。

在文献[2]中，作者针对NOMA下行链路的场景，在考虑用户服务质量和最大发射功率的前提下，研究了子信道分配和功率分配问题。文献[3]研究了上行链路NOMA网络的接入时延最小化问题。作者将其分为2个子问题，即用户调度问题和功率控制问题，并提出了一种迭代算法来解决该问题。在文献和文献中，作者将子信道分配和功率分配联合考虑，但这种联合资源分配问题通常是NP-hard的，采用传统方法优化很难得到最优解。

由于传统方法依赖于对系统的建模，且计算复杂度较高。而机器学习在解决这些复杂的数学问题时表现出了巨大的优势。强化学习(RL: Reinforcement learning)作为机器学习的一个主要分支，可以作为实时决策任务的选项之一。在NOMA系统中，强化学习算法已被用于子信道分配、用户聚类及功率分配等资源分配方法上[6-8]。

深度强化学习(DRL:Deep reinforcement learning)作为深度学习和强化学习的结合，可以直接从高维原始数据学习控制策略提供更快的收敛速度，对于具有多状态和动作空间的系统更加有效。而深度Q网络(DQN:Deep q-network)[9]是DRL的典型算法之一，它将神经网络和Q学习结合起来，通过经验回放和目标网络来解决收敛和稳定问题。深度Q学习已经在许多研究中得到应用，例如多用户蜂窝网络中的功率控制[10]，多小区的功率分配[11]，以及物联网系统[12-13]。

本文针对NOMA系统下资源配置问题，以优化系统最大和速率为目标展开研究。本文将该问题分解为2个子问题分步求解。首先根据信道条件将用户分配至不同的子信道，然后再采用DQN算法，根据用户信道状态信息进行功率分配。通过仿真分析，基于DQN的功率分配方案可以得到较高的系统和速率。

2 系统模型

图1 系统模型

系统总带宽为B，将其均分为N个子信道，每个子信道的带宽为Bs=B/N。用Sm，n表示子信道的分配索引。当用户m分配在子信道n上时，Sm，n=1；否则，Sm，n=0。用pm，n表示第n个子信道上用户m的分配功率。由于NOMA系统中多用户可复用同一资源块，设每个子信道上的最大用户数为M。则第n个子信道上的传输信号为：

(1)

用gm，n表示子信道n上用户m的信道增益。则基站接收端，接收信号的表达式为：

(2)

根据NOMA原理，在接收端采用串行干扰删除技术(SIC)，基站接收多个不同用户的叠加信号，将其按照一定的顺序解调出来。在上行链路中，最优的SIC解码顺序应该是信道增益的降序[14]。因为具有较弱信道增益的设备不会对具有较强信道增益的设备造成干扰。对于子信道n中的用户m，信干噪比可表示为：

(3)

根据香农定理，对应速率为：

Rm，n=Bslog (1+SINR)

(4)

子信道n的和速率为：

(5)

系统的和速率为：

(6)

由上述公式可以看出，系统的和速率和子信道分配、用户的功率分配相关。因此，本文研究的是在上述场景下使系统的和速率最大化的问题，该优化问题可建模为：

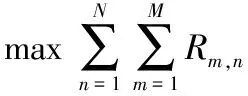
(7)

其中，Pmax是用户的最大发射功率，Rmin是用户的最小数据速率。约束条件C1确保每个用户的发射功率不超过Pmax。约束条件C2保证每个用户的速率不低于最小信号速率。

由于在上述优化问题中，直接找出全局最优解的难度较高。本文将其分成2个子问题：子信道分配和功率分配，逐步去求解该优化问题。

3 子信道分配

在上行链路NOMA系统中，为了在基站接收端进行SIC，需要保持接收信号的差异性。而在同一子信道内，用户的信道增益区别对于最小化簇内干扰也至关重要。用户间信道增益差异越大，对系统性能的提升也越大。为减少接收端SIC解调的复杂度，在本文的分配方法中，每个子信道内将分配2个用户。具体步骤如下。

子信道分配算法伪代码

步骤1：输入总用户数K，组A={}，组B={}。

步骤2：将K个用按信道增益大小排序。

G=sort(K)={g1，g2……gK}

步骤3：如果用户数K为偶数。

A={g1，g2……gK/2}

子信道数为K/2，具体分配为：

……

民间还成立有毛主席像章收藏研究会，总部设在上海。李建明感慨，当时那些收藏家们大都五六十岁了，自己还年轻。如今自己60多岁了，他们已经步入暮年。去年李建明去北京参加一个红色收藏会议，见到几位以前未曾谋面的老朋友，其中有位叫黄淼鑫，送他一本《追梦——毛主席像章收藏31年》。

SK/2={gK/2，gK}

步骤4：如果用户数为奇数。

G=G-g(K+1)/2

步骤5：重复上述步骤3。

4 基于深度强化学习的功率分配

对于上行链路的NOMA系统资源分配，首先基于上述的子信道分配确定分配决策，再通过深度强化学习去确定用户的功率分配。在明确具体的步骤之前，先简要阐述强化学习的理论。

S(状态空间)：在功率分配问题中，将用户信号的信噪比看做状态空间，信噪比r同用户发射功率p、信道增益g等相关，因此，状态空间S可表示为：

S={r1，r2……rK}

(8)

A(动作空间)：在NOMA功率分配中，将对用户发射功率的调整看做是动作空间，可表示为：

A={-1，0，+1}

(9)

-1代表减少用户的发射功率，+1代表增加用户的发射功率，0表示维持不变。

Re(奖励)：Re表示在状态s下采取动作a得到奖励，在本文中，将Re设为系统的优化目标和速率：

(10)

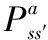
(11)

4.1 Q学习算法

Q学习(Q-learning)算法是一种时间差分算法。状态-行为值函数(Q函数)表明智能体遵循策略π在某一状态所执行的特定行为的最佳程度。Q函数定义为：

Qπ(s，a)=Eπ[Rt|st=s，at=a]

(12)

表示从状态s开始采取动作a所获得的期望回报。其中Rt表示所获得的回报奖励总和：

(13)

γ为折扣因子，表示对于未来奖励和即时奖励的重要性。γ取值位于0～1。

在本文的Q学习算法中，首先由系统环境获得状态s，并初始化Q函数；再根据ε贪婪策略在状态s下采取动作a，转移到新的状态s′，获取奖励r。根据下列方程更新Q值，将其存入Q值表中。其中α为学习速率：

Q(s，a)=Q(s，a)+α(r+γmaxQ(s′，a′)-Q(s，a))

(14)

重复上述步骤若干次，直到迭代完成。

4.2 DQN算法

在具有多维状态时，要遍历每个状态下的行为会花费大量时间，因此采用一个权重为θ的神经网络来近似每个状态下所有可能的Q值，即将该网络作为函数逼近器来逼近Q函数，并通过梯度下降来最小化损失函数：

Loss(θ)=((r+γmaxQ(s′，a′，θ′)-Q(s，a，θ))2

(15)

在本课题中，对用户进行子信道分配后，将其状态空间输入到DQN，采用ε贪婪策略来选择动作：以概率ε在动作空间内选择一个随机动作，以概率1-ε选择具有最大Q值的动作a：

a=argmax(Q(s，a，θ))

(16)

在选择完动作后，在状态s下执行该行为，然后转移到新的状态s′，并获得奖励r。上述信息〈s，a，r，s′〉将被保存至经验回放池中。这些存储信息可被用来训练DQN。接下来，从经验回放池中随机采样一批转移信息，并计算损失函数Loss(θ)。由于连续的〈s，a，r，s′〉信息间是相关联的，这些随机采样的训练样本将会减少信息之间的关联性，并有助于降低神经网络过拟合。

通过随机选择的训练样本，可以得到由目标网络生成的Q值：

Qt=((r+γmaxQ(s′，a′，θ′))2

(17)

其中，目标网络的权重为θ′。用于预测Q值的实际Q网络可通过梯度下降来学习正确的权重。滞后若干时间步后，从实际Q网络中复制权重θ来更新目标Q网络的权重θ′，这样可使训练过程进一步稳定。如图2所示。

图2 DQN主要流程图

5 结果及分析

在本节中，通过仿真结果来评估上行链路NOMA系统中深度强化学习算法的有效性。基站位于小区中心，用户随机分布在小区内。具体参数设置如表1所示。此次仿真在Python3.6上用Tensorflow1.5完成。

表1 仿真参数设置

图3对比了DQN和Q-learning算法的收敛速度和平均和速率。可以看出DQN相较于Q-learning算法更加稳定，相同迭代条件内且所能达到的平均和速率更大，收敛速度更快。这是因为基于神经网络的DQN算法搜索更快，且在状态数过多时，不容易陷入局部最优。

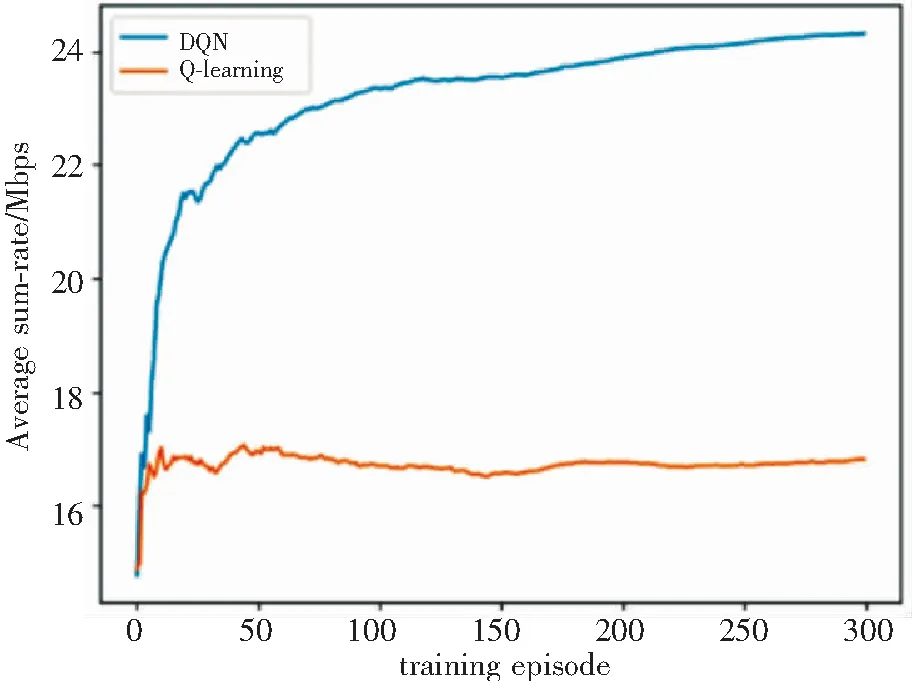
图3 算法的平均和速率比较

图4对比了不同发射功率下DQN，Q-learning以及固定功率分配算法(FPA :Fixed power allocation)的平均和速率。当用户设备采用FPA算法进行功率分配时，可获得略优于Q-learning算法的平均和速率；但FPA始终采用最大发射功率，会导致较高的能量损耗；而DQN由于收敛较快，始终能达到较高的和速率，并且使功率动态分配。

图4 不同功率限制下和速率比较

图5对比了在不同学习速率下的DQN损失函数的收敛情况。学习速率过大会导致函数震荡，迭代过快；学习速率过小则会使函数收敛过慢。从图5中可以看出，当学习速率(learning rate)设置为0.01时，DQN的收敛更加稳定。

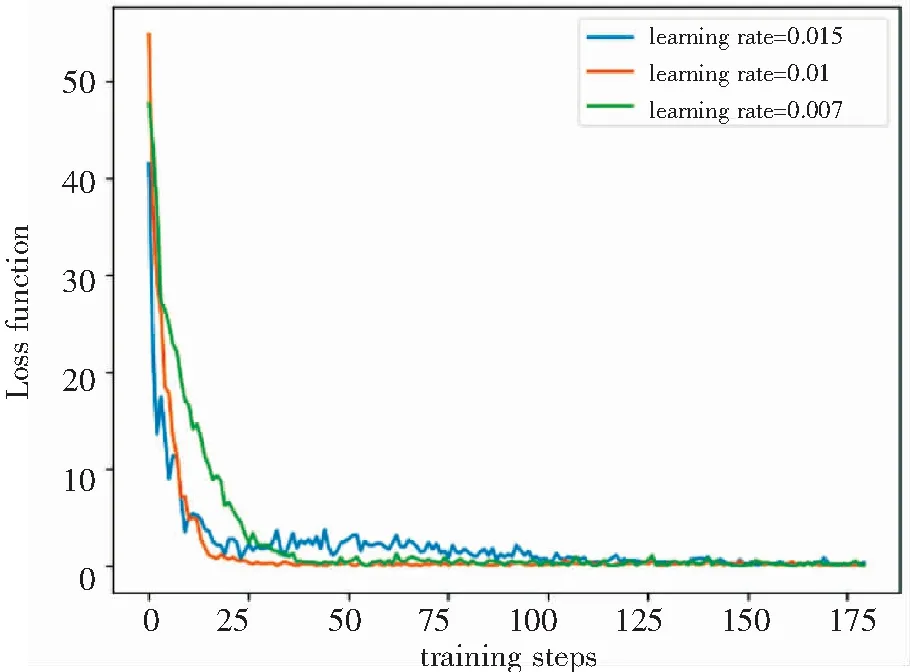
图5 不同学习速率下的DQN损失函数

6 结语

本文主要研究了上行链路NOMA系统资源分配问题，通过子信道分配和基于信道条件的DQN功率分配算法，找到较优的功率分配方案，实现了最大化系统和速率的目标。仿真结果显示:本文提出的Q-learning算法和DQN具备较快的收敛特性。与其他方法相比，DQN算法可以实现更高的和速率，表现出了更好的性能。