基于跳跃风险夏普比率的中国基金收益再度量

袁 靖 , 董雅菁 ,刘 响 , 高 建 , 火 颖

(山东工商学院a.统计学院；b.金融学院，山东 烟台 264005)

一、引言

2020年是我国“十三五”规划收官之年，也是全面建成小康社会的决胜之年，2018年第四次全国经济普查数据显示，我国GDP近年来有了较大幅度增长(2014—2018年我国各年名义GDP分别上调了0.4%、0.4%、0.9%、1.4%和2.1%)。始料不及的是2020年初我国及全世界爆发了新型冠状病毒肺炎疫情，给经济增加了全新的不确定性。不确定冲击对经济运行的影响效应近年来引起学者们及政策制定者的高度重视，究其原因是突发事件频发凸显不确定冲击是影响经济运行的主要冲击，并且对经济变量总体上表现为负面效应[1-2]。

根据有效市场假说，弱式有效性资本市场下，投资者研究过去交易的信息并不会带来超额收益。我国学者根据股票价格波动实证分析视角得到结论即我国股票市场属于弱式有效性市场[3-5]，也就是说，我国基金市场操作只可以追随模拟市场而不能跑赢市场，但是我国基金操作在投资策略上提出以“积极性策略”即以打败市场为投资目标，尤其在面对不确定性事件冲击下。

在基金评价业绩方面，对基金的综合评级基于对基金三方面能力的评价：一是风险管理与构建有效投资组合的能力，体现为风险回报交换的效率，度量指标主要是特雷诺指数、夏普比率和詹森指数；二是选股能力，即通过选择价值被低估的证券而产生市场风险调整后额收益的能力；三是择时能力，即基金根据市场走势的判断，通过调整基金资产行业证券配置以增加或降低市场的敏感度进而跑赢基金市场基准的能力，这也是积极性策略的出发点和宗旨。特雷诺指数、夏普比率和詹森指数中，Sharpe 指数的估计中使用的是总风险指标，因此，Sharpe指数还能够衡量基金经理分散和降低非系统性风险能力。计算标准夏普比率理论假设基金市场收益率服从正态分布，已有大量文献研究发现我国及世界大部分国家基金市场收益率并不服从正态分布[6]，受到其分布形态包括偏度和峰度的显著影响，基于此对标准夏普比率进行改进的方法包括采用收益率风险在险值进行修正[7]、采用比率代替夏普比率[8]、采用Kappa比率代替夏普比率[9]、考虑偏度和峰度构建修正夏普比率[10]、根据厚尾风险度量收益率标准差构建夏普比率[11]以及根据广义矩函数构建夏普比率[12]。但目前学者尚未采用不确定跳跃风险修正基金市场夏普比率计算。

本文构建累积分布函数下高阶矩夏普比率及不确定冲击跳跃风险下夏普比率，重新计算我国基金市场基金组合夏普比率，考察面对不确定时期基金组合是否可以打败大盘指数，从基金投资组合角度再次审视我国资本市场有效性特征。相对于已有文献，本文的边际贡献主要体现在两个方面。第一，丰富了不确定冲击跳跃风险在资本市场应用建模的相关研究。基于非正态分布的不确定冲击跳跃风险解释资本市场波动更贴近现实经济的数据特征，因而已有文献研究已得出结论，嵌入不确定事件的资本市场模型可以较好地解释我国股权溢价之谜、无风险利率之谜、股票市场价格波动之谜及债券市场利率期限结构行为，基金市场作为资本市场的一个重要组成部分，也必然受到非正态分布不确定冲击跳跃风险的影响，因而本文的研究结论将极大的丰富不确定冲击模型在我国资本市场应用的相关研究。第二，对我国资本市场有效性研究提供更强有力的识别条件。以往文献对资本市场有效性验证均基于资本市场价格波动特征进行，而根据法玛的有效市场假说资本市场若为有效性市场，则基金收益率无法打败股市大盘指数。美国目前已有越来越多的大型基金操作策略依据美股市场中强有效特征构建被动型基金，随着中国基金市场越来越具有去散户化特征，我国大型基金在面对危机未来的策略时采用消极性策略还是积极性策略？是企图打败市场还是只能跟随模拟市场？本文的研究以我国资本市场弱有效性特征为前提，考量2007年至 2020年的14年间的股票型基金与上证A股市场收益率，为我国资本市场有效性研究提供更强有力识别，并为基金公司及投资者未来投资策略提供数据检验。

二、研究假设、研究设计及样本数据

(一)研究假设

Markowitz的投资组合理论[13]最早提出了对于金融资产风险的计算方法，并准确计算了证券投资基金的风险和收益，但Markowitz通过计算组合中各资产的协方差矩阵来计算风险，其方法过于复杂，当时的计算机技术远没有今天发达，因此难以得到大范围的推广和应用。学者们开始尝试建立更多新的更加实用的基金业绩评价模型，其中以Treynor、Sharpe和Jensen提出的三个风险调整收益指标[14-16]最具代表性，这三个指标分别是特雷诺指数、夏普比率和詹森指数，这三个指标的出现大大简化了基金业绩评价计算的复杂性。夏普比率使用投资组合收益率的标准差作为其风险度量指标，计算了投资组合单位风险下获取的收益情况，该标准差的几何意义即投资组合和无风险利率两者连线的斜率。夏普比率越大，说明投资组合承受单位总风险所获取的超额风险调整收益越高。

对于夏普比率，其理论假设是收益率呈现正态分布，但现实经济极值事件或者厚尾事件比正态分布更经常出现，正态分布的对数收益率前两阶矩是有限值，高阶矩为0，而厚尾的对数收益率高阶矩不等于0，不确定事件导致的跳跃风险下资产价格对数收益率是负偏的(偏度是负数，就是三阶矩)，峰度值较高。

本文将基于累计生成函数重新构建高阶矩的夏普比率及不确定冲击的跳跃风险下夏普比率，并试图回答如下理论假设：

假设1：我国基金市场收益率呈现明显负偏高峰度的非正态分布。

假设2：我国基金市场夏普比率受到不确定冲击的跳跃风险的显著影响。

假设3：经过十几年的发展，我国基金市场已经从非有效性市场逐渐进入弱式有效性市场，按照法玛的有效市场理论，中强有效市场将会是我国未来发展的方向，美股基金市场从上世纪90年代开始偏好消极性策略，即构建基金组合只能模拟大盘指数，这一应用有近30年发展历程。未来我国基金市场越来越成熟，也会在短时间内趋于相同的选择，以基础分析为主要分析策略的大型基金，其收益打败大盘指数变得越来越困难，随着我国资本市场越来越成熟，拥有卓越分析能力的优秀基金毕竟是稀缺的，大多数基金只能以跟随和模拟大盘指数而非跑赢大盘指数收益为目标，尤其面对不确定冲击的危机时期。

(二)基于累计生成函数高阶矩下的夏普比率构建

对于任意随机变量X，均有

m(θ)≡Eexp(θX),K(θ)≡logEexp(θX).

且对于所有的θ，期望值均存在；则称m(θ)为矩母函数，K(θ)为累积生成函数(cumulative generating function，简称CGF)。累积生成函数包含了关于变量X所有阶矩的信息，我们通过幂序列的形式将K(θ)展开得：

(1)

其中，αn代表变量X的第n阶矩。从代数的角度看，α1代表变量X的均值，α2代表变量X的方差，α3/σ3代表变量X的偏度，α4/σ4代表变量X的峰度，如此类推。

市场存在两类资产，一类是货币市场的无风险资产，一类是资本市场基金指数，假定指数基金不分红，考察两期投资，t={0,T}，到期时无风险资产价格为B(T)，指数基金价格为P(T)，

B(T)=B(0)exp{rf}.

(2)

P(T)=P(0)exp{r}.

(3)

r为基金价格对数收益率，rf为无风险利率，基金收益率等于其投资期内平均增长率减去其均值，即：

r=μ+X-k(1).

(4)

μ为平均增长率，X为随机变量，k(1)为X的一阶矩即均值，K(θ)为X的累积生成函数，

(5)

将基金价格表示为CGF函数形式为：

(6)

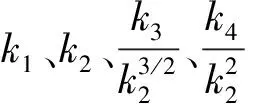
(7)

计算基金价格对数收益率的均值及方差表示为：

C(1)=μ,C(2)=2μ+K(2)-2K(1).

(8)

得到标准夏普比率Sharpe-ratio:

(9)

性质1：夏普比率不仅依赖于收益率的均值及方差即前二阶矩，还依赖于偏度峰度等所有高阶矩。

(三)基于不确定冲击的跳跃风险下的夏普比率构建

随着经济全球化的不断深入，中国经济越来越多地暴露在国际国内经济金融危机冲击的风险中，严重自然灾害冲击也愈加频繁。Barro[17]对上个世纪100年期间内OECD国家做了统计分析，发现样本期内，有60次的不确定导致人均GDP下降15%以上，其中1929—1933年间主要工业国家人均实际GDP下降幅度均在16%～33%之间，两次世界大战期间，法国、德国、澳大利亚等战区国家人均GDP下降幅度最低达到16%，最高达到64%。

将不确定对经济造成的跳跃风险引入夏普比率，

X=W+Z,W▯N(0,σ2),

(10)

将以上设定带入CGF函数：

(11)

得到对数收益率r的矩：

c1=μ-K(1)+k1,k1=λμJ

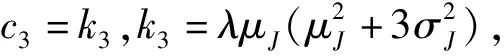
(12)

将以上参数带入得到不确定跳跃风险下的夏普比率Sharpe-ratioDisaster为：

(13)

性质2：不确定冲击带来的尾部跳跃性风险会显著影响夏普比率。

(四)数据选取及说明

2008年金融风暴及之后的欧债危机等不确定冲击事件给全世界绝大多数国家经济造成严重的影响效应，我国股市也在2008年及2015年、2016年受到重创，基于此本文将样本区间选择为2007—2020年。由于本文的研究目的是基金市场与大盘指数收益率特征及对比，因此选择股票型基金为样本框，即2007—2020年存续的股票型基金，其中消极型投资策略的基金样本中，选取华安上证180ETF(上证50交易型开放式指数证券投资基金)及华夏上证50ETF(上证180交易型开放式指数证券投资基金)，对于积极型策略基金，在万得数据库中的开放型基金中选取了普通股票型基金、偏股混合型基金和平衡混合型基金中自2007年1月开始有日收益数据的基金作为“积极型投资策略”基金的选取样本，并且基金中债券类净值平均不超过基金组合净值的10%的基金，筛选符合条件的主动型基金有115支。样本基金共117支。

基金复权净值是对基金单位净值进行了复权计算，考虑基金的分红或拆分，因此本文基金收益率计算采用其基金复权净值数据，计算方式采用对数收益率计算方式；对于大盘指数收益率，本文采用上证A股数据，关于股票市场收益率，考虑以流通股市值为权重加权平均，同时还要考虑配股、送股、拆细的影响以及红利再投资。股票收益率的计算方法通常有两种：一是采用对数收益率，二是采用百分比收益率。由于对数收益率具有很多良好的统计特征，因此在有关金融资产定价领域多采用对数收益率的形式。鉴于此，本文亦采用对数收益率进行计算。以上数据来源均为万得经济数据库。

三、我国基金市场收益率分布特征及夏普比率计算

(一)我国基金市场的收益率特征以及夏普比率

选取的117支基金和上证A股大盘指数，样本数据共118支投资组合，对所有样本数据2007年1月至2020年12月共14年周期的基金收益率偏度系数及峰度系数进行计算，使用Jarque-Bera检验统计量对基金收益率进行正态性检验(由于计算结果表篇幅太长，未放入论文中，感兴趣可向作者索取)，结果如下：(1)偏度系数结果显示样本数据对数收益率偏度系数均为负偏尖峰分布，偏度平均值为-0.687，偏度最小值为-0.248，偏度最大值为-1.201；(2)峰度系数结果显示峰度平均值为4.959，峰度最小值为3.771，峰度最大值高达7.939，负偏度使得收益率下降概率超过上升概率，从而增大投资者蒙受损失的可能性，高峰度又使得极值事件发生的概率增加；(3)我国117支基金及上证A股Jarque-Bera检验统计量p值显示拒绝原假设，即均不服从正态分布，这意味着计算标准夏普比率衡量基金收益率风险存在较大偏差。

对117支基金及上证A股的标准夏普比率Sharpe-ratioN进行计算，将其月均值做图如下：

根据图1结果，将我国117支基金及上证A股的夏普比率与我国同时期股票市场波动走势进行比较分析得到如下结论：

图1 117支基金及上证A股的夏普比率月均值

(1)夏普比率出现波动较大的时期分别为：2007年4月夏普比率均值达到最高值0.535即跌至0.26，到6月跌至最低点0.01，7月回升，但到11月跌至-0.39，12月又回升至0.37；2008年夏普比率一直处于低点运行，其中从9月的-0.14下跌至10月的-0.55，这是样本数据中的最低点；2009年夏普比率回升，仅8月出现较大波动，跌至-0.41；2010年夏普比率稳步回升，其中7月回升至全年最高点的0.36；2011年10月跌至-0.43；2012年全年夏普比率水平较高，有轻微波动，其中12月更是回升至0.49；2013年波动较大的月份是5月和6月，从最高点0.41跌至全年最低点-0.33；2014年夏普比率全年走势平稳；2015年6月从0.32跌至-0.52，这是样本数据中跌幅最大的一次；2016年1月也从0.14跌至-0.41；2017—2019年走势较平稳；2020年6月夏普比率达到高值0.42，随即8月跌至-0.33,11月有所回升。

(2)我国样本数据基金夏普比率波动走势与我国股市大盘指数波动走势完全一致，尤其上证A股波动2008年1月5 000多点跌至10月的1 600多点，2015年6月15日至7月9日，短短18个交易日上证指数从5 178.19暴跌至3 373.54点，最大跌幅达34.85%，2015 年7 月初，以证金公司为代表的“国家队”开始强势入市拯救股市，夏普比率在2008年和2015年波动幅度最大，但是2014年和2018年大盘指数波动最小，夏普比率波动走势亦平稳。数据显示我国基金走势与大盘指数收益走势表现一致。

(3)将上证A股夏普比率与117支基金夏普比率对比，在股市走势平稳甚至上升期，上证A股夏普比率居中，但是在不确定冲击下，上证A股夏普比率的计算结果也非常高，这样，2008年所有样本数据夏普比率均值分别为(-0.19、0.02、-0.36、0.02、-0.17、-0.36、0.02、-0.32、-0.14、-0.55、0.16、0.06)，但上证A股夏普比率分别为(0.21、0.06、-0.15、0.06、0.18、-0.31、0.04、0.26、0.09、-0.31、0.35、0.15)；2015年股灾期间，所有样本数据夏普比率均值分别为(0.12、0.31、0.48、0.30、0.32、-0.52、-0.17、-0.19、-0.03、0.33、0.10、0.14)，但上证A股夏普比率分别为(0.18、0.32、0.52、0.55、0.38、-0.08、0.16、0.13、0.11、0.38、0.35、0.28)；表明在不确定冲击下，基金并没有体现出其优秀的择时能力。

结果表明:我国基金市场收益率呈现负偏高峰度的非正态分布。

四、不确定冲击跳跃风险下的我国基金市场夏普比率

(一)不确定冲击跳跃风险下的我国基金市场夏普比率构建及特征

1.参数校准

2.不确定冲击的跳跃风险下我国基金市场夏普比率构建

由于我国117支基金与上证A股指数收益率均为高峰分布，而高峰分布意味着不确定性冲击影响效应极大，因而重新计算我国117支基金与上证A股指数,2007—2020年考虑不确定冲击跳跃风险修正下夏普比率Sharpe-ratioDisaster，并计算其与标准夏普比率Sharpe-ratioN的差值做图如下：

根据图2结果得到如下结论：

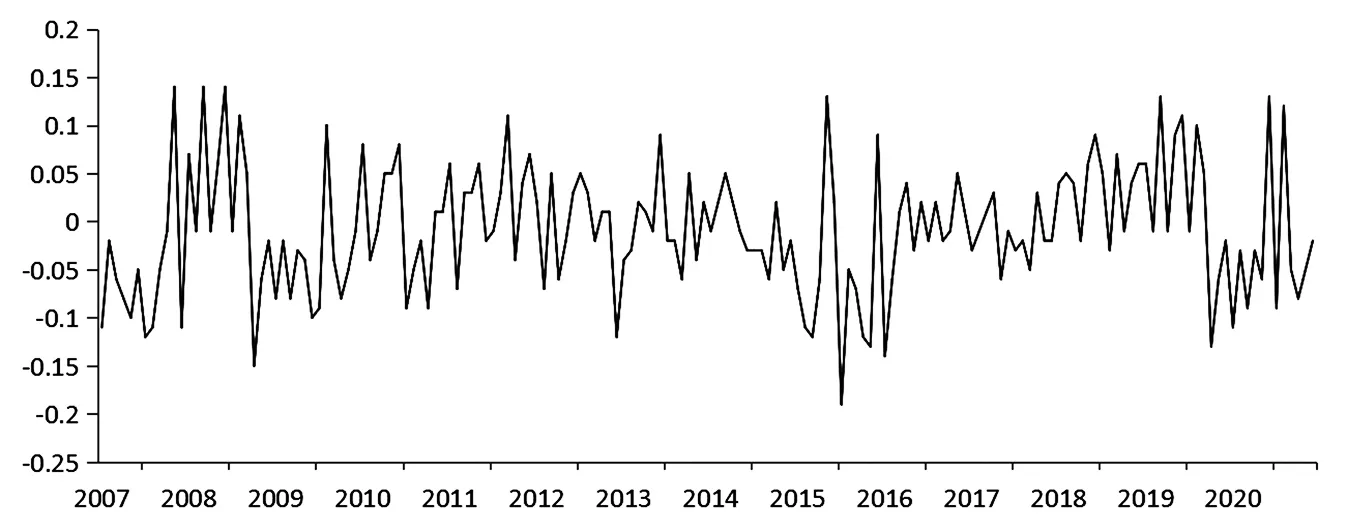
图2 117支基金和上证A股不确定冲击下夏普比率与标准夏普比率均值差值

(1)不确定冲击下夏普比率计算结果与标准夏普比率有较大显著差异，尤其是经济危机时期，2008年9月差值达到15%，2015年7月差值达到19%，这也是样本数据差值最大的时期，差异较大的时期与夏普比率波动较大的时期一致，说明面对不确定冲击的尾部跳跃风险，标准夏普比率偏差太大。

研究结果发现，我国基金市场夏普比率受到不确定冲击的尾部跳跃风险的显著影响。

(二)面对不确定冲击我国基金与上证A股大盘指数表现对比分析

弱式有效性资本市场下，投资者研究过去交易的信息并不会带来超额收益，基金市场是否比大盘指数表现更优？将上证A股标准夏普比率及不确定事件冲击下夏普比率排名，目的是比较大盘指数与整个基金市场业绩表现，做图如下：

根据图3结果得到如下结论：

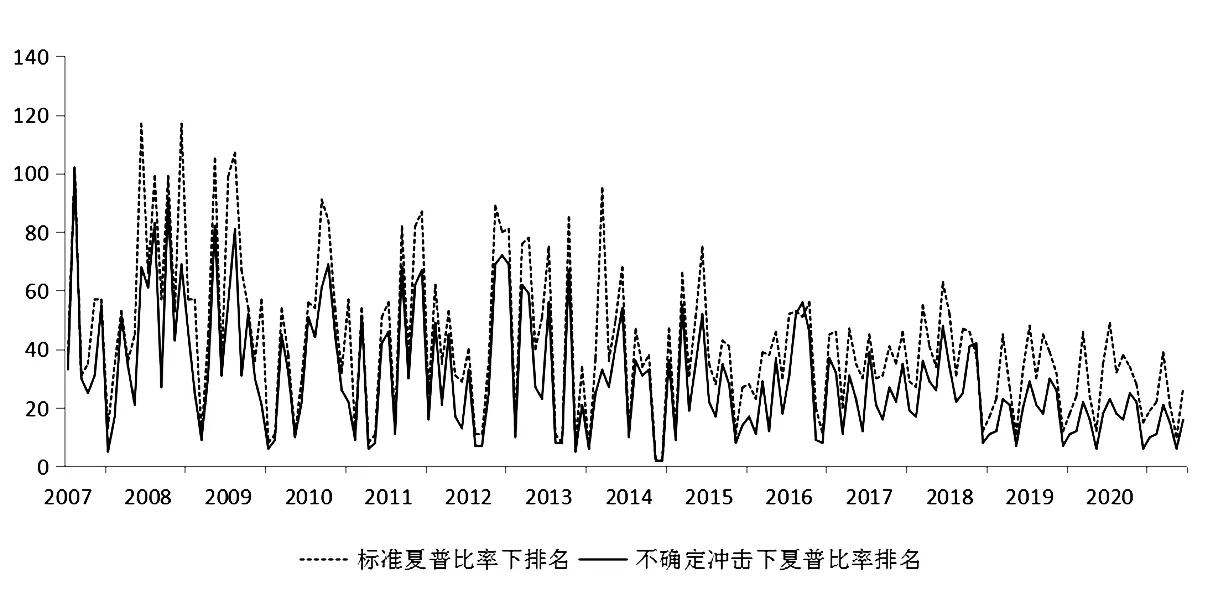
图3 上证A股夏普比率排名及不确定冲击下夏普比率排名

第一，我国上证A股不确定冲击下夏普比率排名比标准夏普比率下排名均有所提高，尤其面对不确定冲击，2008年6月标准夏普比率下排名为第117，经过不确定冲击尾部跳跃风险修正夏普比率下排名为第69，2015年7月标准夏普比率下排名为第28，经过不确定冲击尾部跳跃风险修正夏普比率下排名为第17，说明上证A股抵抗不确定事件冲击下尾部跳跃风险的能力优于大部分基金组合。

第二，我国上证A股标准夏普比率排名下最差名次为第117(2007年12月和2008年6月)，最优名次为第2(2014年5月和2014年6月)；不确定冲击修正下夏普比率排名最差为第101(2007年2月)，最优名次为第2(2014年5月和2014年6月)。

第三，无论是标准夏普比率下排名还是不确定冲击修正下夏普比率排名，我国上证A股排名走势是越来越优，尤其2017年之后。

第四，近年来我国大盘指数扩容很快，其抵御风险的能力越来越强，但是基金市场基金组合选取跟不上步伐，其模拟性越来越差。

研究结果发现我国基金市场整体收益率不如上证A股，也就是说，我国基金市场已经从弱有效性市场逐渐走向中强有效性市场，以基础分析为主要分析策略的大型基金，其收益打败大盘指数变得越来越困难，随着我国资本市场越来越成熟，拥有卓越分析能力的优秀基金毕竟是稀缺的，大多数基金只能以跟随和模拟大盘指数而非跑赢大盘指数收益为目标，尤其面对不确定冲击的危机时期。

五、结论

我国基金市场收益率并非满足正态分布假设，因而采用标准夏普比率进行评级存在较大偏颇；近年来我国A股市场连续出现崩盘事件，而我国基金市场一直提出以“积极性策略”打败市场，对基金市场是否可以达到此目标重现计算科学夏普比率进行评价。本文通过构建累积生成函数高阶矩下夏普比率，并将不确定事件的跳跃风险嵌入其中，对我国基金市场表现进行评价比较，并对我国资本市场有效性进行了强有力识别。得到以下结论：

第一，2007—2020年的我国117支股票型基金与上证A股市场收益率呈现明显负偏高峰度非正态分布，而是明显负偏高峰分布，这说明我国基金市场操作存在较大下降风险，并容易受到极值事件影响。

第二，我国117支基金及上证A股收益率夏普比率受到不确定冲击的跳跃风险的显著影响，差值最大达到了19%，比美国基金市场小很多，其中很大原因是面对不确定冲击，我国政府在危机时期进行了直接干预，这对于稳定我国资本市场发展及保护投资者效益是非常必要的。

第三，无论是标准夏普比率下排名还是不确定冲击修正下夏普比率排名，我国上证A股排名走势是越来越优，尤其2017年之后，经过十几年的发展，我国资本市场已经从非有效性市场逐渐进入弱式有效性市场，中强有效市场将是未来发展方向，以基础分析为主要分析策略的大型基金，其收益打败大盘指数变得越来越困难，随着我国资本市场越来越成熟，拥有卓越分析能力的优秀基金毕竟是稀缺的，大多数基金只能以跟随和模拟大盘指数而非跑赢大盘指数收益为目标，尤其面对不确定冲击的危机时期。

本文的研究对于我国建立防范和应对金融市场危机的机制具有一定的参考价值。由于基金市场在面对不确定冲击时表现不能优于大盘指数，因而机构投资者和个人投资者在构建投资组合抵御风险时应紧紧追随大盘指数，而面对危机市场则需要借助政府的力量，解决不确定冲击尾部风险(尤其是左尾风险)效应以达到市场稳定的目的。本文采用累计生成函数对标准夏普比率进行修正，计算了四阶矩下夏普比率及不确定冲击的尾部跳跃风险下夏普比率，但是没有继续推导无限阶矩下夏普比率，其计算结果是否与本文结果存在较大差异？这将是后续进一步研究的主要内容。