我国城市房地产风险空间溢出研究——基于35个大中城市的空间面板模型分析

张金鑫

(1.国家统计局 固定资产投资统计司，北京 100826；2中共中央党校 经济学教研部，北京 100089)

一、引言

1998年城镇住房制度改革及其深化以来，我国城镇化进程加速推进，使得房地产业快速发展，并成为推动国民经济发展的重要动力。近年来，随着我国经济由高速增长阶段转向高质量发展阶段，受城镇化步伐的放缓及人口老龄化等因素影响，房地产市场的发展已由需求大于供给的总量失衡阶段转向总量均衡结构分化严重的新阶段。同时，伴随着大规模高速铁路网络建设，城市间的时空距离被大大压缩，人们的居住、就业等活动空间不断扩展，城市间房地产市场的联系不断加深。当前，在资本市场的推动下，我国城市房地产投资与消费逐渐摆脱了原有地域界限，向全国更大范围内拓展；同时在人口大规模流动情况下，居民的住房需求与生产性需求也在逐渐摆脱地域限制。资本和人口等房地产市场要素的跨区域流动，增强了城市房地产风险的空间扩散性。

目前，国内外学者对房地产市场风险空间溢出效应的相关研究较为丰富，主要研究集中在房地产价格泡沫空间传染性以及泡沫风险空间联动机制等方面[1-3]。Costello 等基于VAR模型评估了澳大利亚大城市房价基本价值，实证分析了房地产价格泡沫风险在区域间的传染效应[4]。Nneji等)运用机制转换模型和多变量泡沫溢出模型分析了美国区域房地产市场泡沫及其空间传染性，研究发现，美国各地区间房地产泡沫存在显著的空间传染效应，并且传染效应不完全依赖于地理距离，不仅是单一方向而是多方向联动的[5]。韦汝虹等运用空间计量模型实证分析了35 个大中城市房地产泡沫的空间传染性，研究表明我国城市房地产泡沫具有空间传染性，其传染能力随时间推移逐渐增强，在空间上表现为由东部沿海向西北内陆递减[6]。李伦一和张翔使用对数周期性幂律模型(LPPL)对100 个大中城市房地产市场价格泡沫进行了测度，并运用空间计量模型对房地产市场价格泡沫和空间传染效应进行了实证分析，结果表明空间传染性会导致房价的波动效应放大[7]。吴清婷等引入地理学空间视角，测度35 个大中城市房地产泡沫水平，并分析空间分布特征和空间传染性，研究表明我国城市房地产泡沫不仅具有空间传染性，并且其空间传染性具有明显的区域差异性和动态特征[8]。

梳理上述研究文献发现对城市房地产风险全面性测度还存在一定缺陷，城市房地产投资、库存等维度风险的空间集聚效应、溢出效应尚缺乏深入探讨。为进一步研究城市房地产风险的空间聚集特征以及房地产风险与经济增长在空间上的相互关系，本文对35个大中城市1999—2018年有关房地产风险和经济增长的空间面板数据，构建空间自回归模型(SAR)、空间误差模型(SEM)等空间计量模型，对其空间溢出关系的理论进行实证检验，对城市间的空间互动关系进行定量研究。

二、基于动态因子模型的城市房地产风险综合度量

我国城市房地产市场发展体现出明显的体制转轨特征，数据的历史长度、稳定性和连续性不理想，利用常规时间序列历史数据回归建模进行外推预测或是以市场数据为基础的监测方法都不太适用。相对而言，综合指数法简明清晰，且可以灵活与其他模型结合使用。同时，动态因子模型对经济、金融等高维数据进行降维处理十分有效，通过估计和解释各变量的共同波动因子，来研判经济周期波动并进行预测分析。房地产市场风险波动是通过一系列变量传递和扩散的，任何一个变量本身的波动都不足以代表市场的整体波动，因此采用动态因子模型构建综合指数分析较为适合。

(一)房地产综合风险指标体系构建

依据房地产市场均衡理论，当城市房地产市场均衡失衡出现供大于求或者供不应求时，会导致库存过剩或供应短缺，并引起房地产价格的波动。同时，我国城市房地产发展过度依赖金融市场支持，加上房地产市场自身平衡和调节能力弱、对政策依赖性强，市场机制难以有效配置资源导致市场失灵。为了客观反映城市房地产风险的整体状况，遵循综合性、全面性和重要性原则，本文借鉴以往研究成果，综合考虑房地产开发风险、融资风险、价格风险、库存风险和城市环境风险五个维度建立指标体系。具体指标选取见下页表1。

本文将选取1999—2018年35个大中城市表1中的相关指标数据，综合运用主成分分析和动态因子模型构建房地产风险综合指数，对各城市的房地产市场风险进行度量。以上各指标数据来源于中国城市统计年鉴、中国房地产统计年鉴。同时为了消除不同量纲之间比较困难的问题，每个指标数据都进行标准化处理。

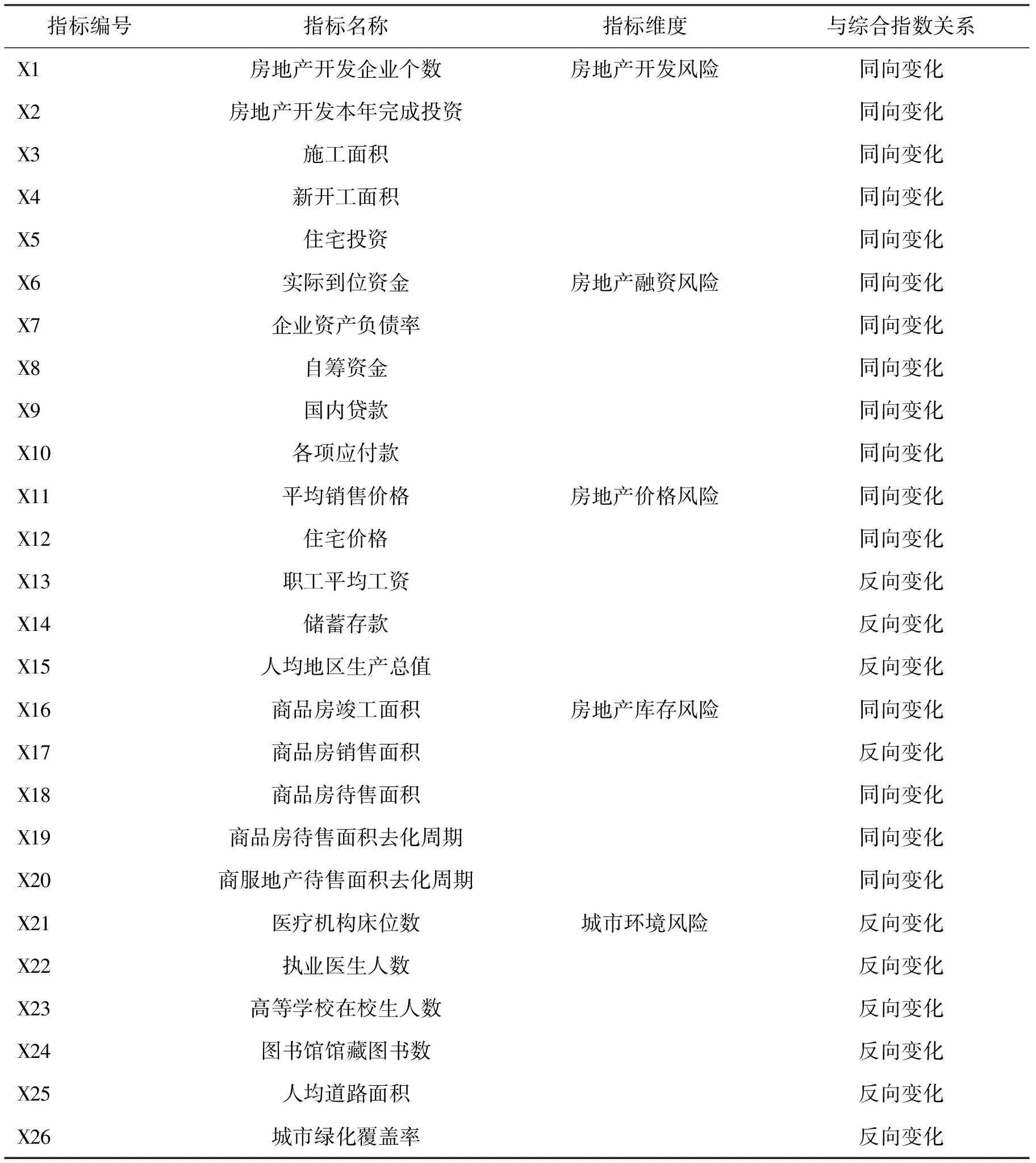
表1 房地产风险综合指数指标选取

(二)城市房地产风险综合指数测度

1.主成分分析与各维度风险指数。主成分分析可以将原始数据指标转化成少数几个主成分，即通过降维来实现简化信息。主成分分析通过正交变换将一组可能存在相关性的原变量转换为一组线性不相关的新变量，转换后的这组综合变量被称为主成分。通常主成分用原来多个指标作线性组合处理。本文将首先通过主成分分析方法从房地产开发风险、融资风险、价格风险、库存风险、城市环境风险五个方面提取主成分作为可观测因子。

以房地产开发维度风险为例，使用SPSS软件对房地产开发风险相关变量房地产开发企业个数(X1)、房地产开发本年完成投资(X2)、房屋施工面积(X3)、新开工面积(X4)、住宅投资(X5)进行主成分分析，得到各个指标与因子载荷数乘积之和为主成分得分，具体如下：

F=0.867X1+0.901X2+0.977X3-0.262X4+0.650X5.

(1)

在此主成分得分F定义为房地产开发风险指数(DRI即开发维度风险因子)。以此类推分别得到房地产融资风险指数(FRI)、房地产价格风险指数(PRI)、房地产库存风险指数(SRI)、房地产城市环境风险指数(CRI)。

2.动态因子模型与综合风险指数。本文参照Stock and Watson 状态空间形式的动态因子模型，构建城市房地产综合风险模型，模型参数使用Kalman滤波技术求出的极大似然估计[9]。模型具体形式如下：

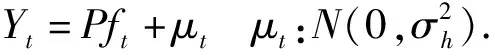
(2)

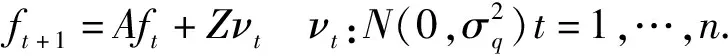
(3)

其中矩阵P和A的元素分别为ρ和α。

测量方程中用主成分分析得出的各维度风险指数为可观测变量Y，然后通过模型求出不可观测变量f，也就是房地产风险综合指数(RRI)，一个引发房地产风险各指标共同运动的潜在因子。使用STATA15.1软件估计动态因子模型，动态因子模型的主要参ρ、α数估计结果见表2所示，这里不考虑常数项C，取t= 1，即潜在因子为1阶自回归形式AR(1)。

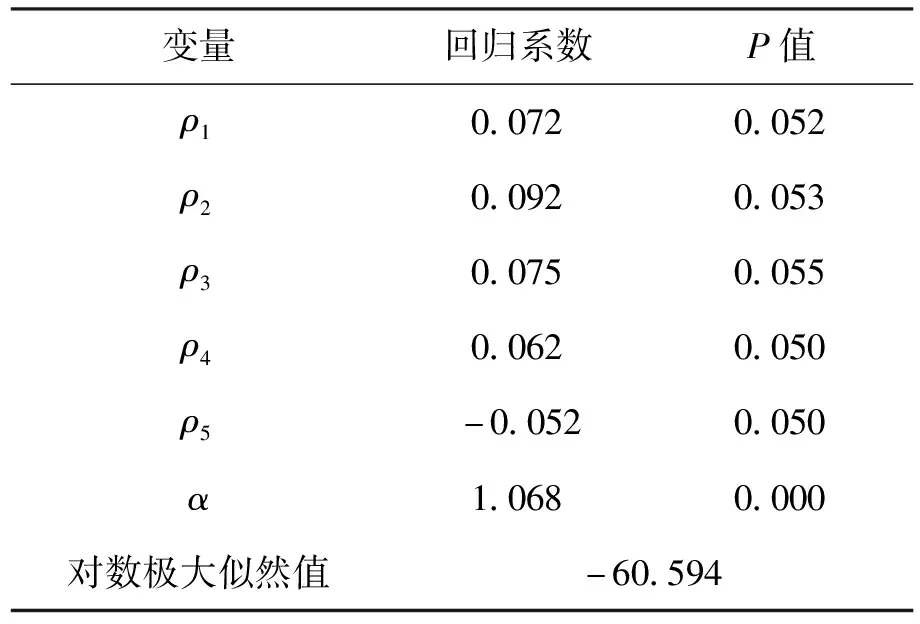
表2 动态因子模型参数估计结果

因篇幅原因，在此仅给出1999—2018年北京房地产风险综合指数测度结果，见表3。

表3 1999-2018年北京房地产风险指数

从35个大中城市各维度风险和综合风险走势看，一线城市中，北京和上海两个超大都市，一方面由于房屋价格和地价高企地方政府采取了十分严格的房地产调控措施，另一方面两个城市分别作为政治文化中心和经济中心其经济发达、公共设施服务水平高，从同一年份与其他城市的风险对比看其开发风险、融资风险、价格风险、库存风险处在前列，而体现高质量发展的城市环境风险较小。二线城市中，以南京为例近年来地价和房价上涨较快、房地产开发规模不断扩大，从2012年和2018年结果看，开发风险指数由0.27上升到1.22、价格风险指数由0.73上升到2.40，而库存风险指数由0.48下降到-0.01、环境风险指数由-0.47下降到-0.74。综合对比看，35个大中城市房地产风险总体上呈现如下特点：一方面房地产风险大小与经济发达程度正相关；另一方面随着经济发展公共设施的不断完善、城市环境的不断优化会降低房地产风险程度。

三、城市房地产风险空间计量的实证分析

(一)地理学第一定律与空间计量经济学

Waldo Tobler首次提出“地理学第一定律”，认为任何事物都是与其他事物相关的，只不过相近的事物关联更紧密(Everything is related to everything else, but near things are more related to each other.)[10]。此定律通常可理解为空间相关性定律，即事物之间距离越近，它们的相关性越大；而距离越远，事物间相异性越大。到了20世纪70年代，随着信息技术和地理信息系统(GIS)的发展应用，使得把空间数据(包含地理信息的数据)与相关经济特征结合起来进行计量研究成为可能；同时，在这一时期经济理论研究中，通过引入空间因素后研究经济行为人之间互动产生的同伴效应、相邻效应、溢出效应、网络效应等逐渐成为热点。Paelinck首次提出空间计量经济学概念，空间计量经济学不仅可以解释地理单位的关系，而且可以解释个人、公司、政府之间通过网络产生的相关关系[11]。

与西方国家(如实行联邦制的美国、德国)相比，我国地区行政管理部门间的联系更为紧密，因而与地区经济发展和调控政策关系密切的房地产市场发展的空间相关性更为显著。对区位特征和邻里特征明显的城市房地产市场而言，具有相似地理环境和经济发展程度的地区发展会出现趋同倾向。同时由于房地产风险的空间溢出效应也会促使城市间房地产风险集聚积累并出现空间上的非均匀分布。因此，本文运用空间计量方法研究城市房地产风险空间集聚，分析35个大中城市经济发展与房地产风险的空间相关性，不仅技术方法上适用可行，而且对因城施策、协同施策的调控机制具有重要的启示意义。

(二)空间权重矩阵和空间自相关指数

1.空间权重矩阵。空间计量经济学中一个核心问题就是研究对象空间结构的设定。学者们大多通过度量区域间的空间距离或空间邻接关系，构建空间权重矩阵作为空间计量分析的基础。空间权重矩阵(spatial weighting matrix)的一般形式如下：

(4)

其中，区域i与区域j之间的距离为wij，主对角线上元素w11=…=wnn=0(同一区域自身的距离为0)，因此空间权重矩阵为对称矩阵。空间权重矩阵的构建原则需满足空间相关性随着区域间“距离”的增加而减少的原则。这里的距离既可以是地理上的相邻或欧氏距离，也可以是经济上交往关系的远近，甚至还可以是社会学意义上的人际关系的亲疏。在本文空间计量研究中，选取空间权重矩阵分为以下几种形式。

(1)简单空间权重矩阵。简单的空间权重矩阵，是根据区域之间的空间相邻情况使用0和1元素进行定性标记，也就是简单的二进制空间权重矩阵。本文根据城市间的距离定义相邻关系。如城市i和城市j之间的距离为dij，空间权重定义为：

(5)

综合考虑，本文将临界距离d设定为500公里，即高铁通行时间在两小时以内。

(2)基于距离的空间权重矩阵。距离空间权重矩阵，是使用城市间距离的相对大小从定量角度定义空间权重结构。通常用距离的倒数(inverse distance)作为矩阵的元素，即：

(6)

其中，本文距离dij是基于城市经纬度的地理距离。

(3)经济空间权重矩阵。一些学者研究发现，相邻地区经济上的相互关系并不完全相同。林光平等(2005)使用基于地理相邻关系的简单权重矩阵研究我国28个省市间的实际人均GDP收敛情况，发现河北省虽然地理上与北京、天津、山西、内蒙古、山东、河南相邻，但河北省与北京、天津的经济密切程度明显高于其他省份[12]。因此，他们使用地区间人均GDP的差额来度量地区间的经济距离，并将经济空间权重矩阵定义为：

W′=W×E.

(7)

2.空间自相关指数。空间计量统计分析假设变量之间存在空间依赖性，并且变量之间存在空间范畴的相关性，即空间自相关(spatial autocorrelation)。因此，为考察地区变量间能否使用空间计量经济方法，首先要确定数据是否存在空间依赖性。与时间序列数据相比，空间数据自相关可以在多个方向上产生，并且数据间可以相互影响，因而更加复杂。受区域空间的相互集聚及扩散作用，同一区域内的数据表现出各种空间相关性(位置相近的区域具有相似的变量特征)。如果区域间高值与高值，低值与低值聚集在一起则被称为“正空间自相关”，或高值与低值相邻被称为“负空间自相关”。在空间计量分析中，主要通过空间自相关指数来衡量空间自相关程度。最常见的空间自相关指数为莫兰指数(Moran，s I)[13]。

(8)

(9)

莫兰指数I的取值范围在[-1,1], 小于0表示负自相关，即高值与低值相邻。当莫兰指数I接近于0，则表明空间分布是随机的，不存在空间自相关。莫兰指数可作为观测值与其空间滞后(spatial lag)值的相关系数。

使用Stata15.1软件，分别用城市间0-1相邻空间矩阵、距离倒数的空间权重矩阵和经济空间权重矩阵，对35个大中城市房地产综合风险(lnRRI)波动计算Moran's I，检验其全局空间自相关性。检验结果如下页表4所示。

从表4来看，首先除0-1相邻矩阵形式的空间权重矩阵(p值不显著)外，反距离矩阵和经济空间局测量的35个城市之间房地产风险都具有正的空间聚集现象，空间溢出效应明显。其次，相比于经济空间矩阵，反距离矩阵求得的Moran'I 指数在数值上相对较小，说明城市间经济交往因素对房地产风险空间相关关系的影响大于纯地理因素影响。最后，经济空间矩阵所求得的Moran'I 指数的在10%显著水平上通过检验(大部分年份在1%显著水平通过检验)，显著性高于逆距离矩阵。总之，经济距离权重矩阵求得的城市房地产风险空间自相关性显著，Moran'I 指数基本在0.25 以上说明空间溢出效应较强，城市房地产风险存在集聚特征。同时，根据空间相关性结果，下文空间计量分析中将使用经济空间矩阵作为权重矩阵。

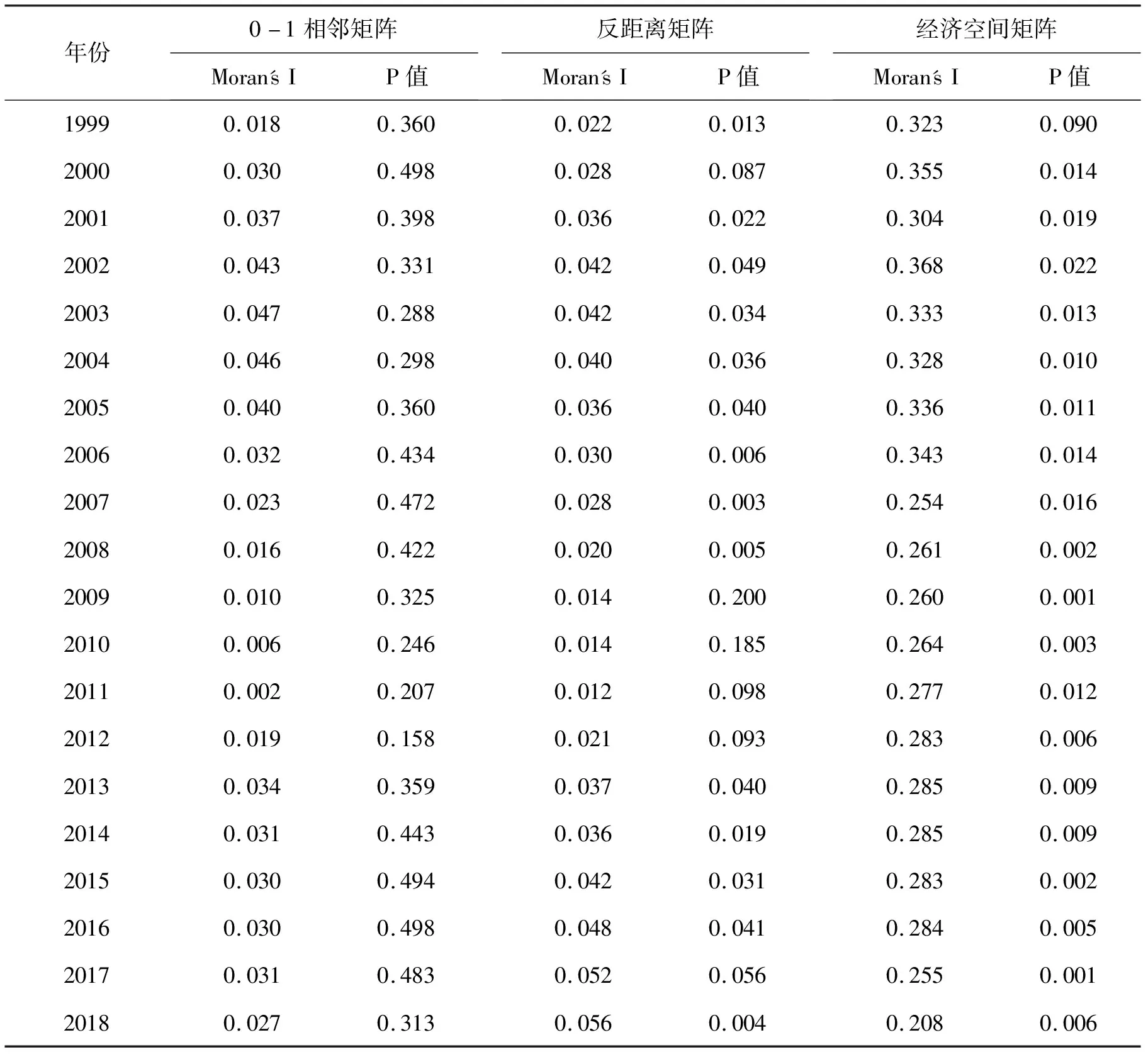
表4 35个大中城市房地产风险全局莫兰指数

(2)局部莫兰指数。全局莫兰指数考察整个空间序列的空间聚集情况，若考察某区域i附近的空间集聚情况，则使用“局部莫兰指数”(local Moran，s I)

局部莫兰指数含义与全局莫兰指数相似，当Ii>0时，区域i的高(低)值被周围高(低)值所包围；当Ii<0时，区域i的高(低)值被周围低(高)值所包围。将观测值和均值偏差与其空间滞后值画成散点图，称为“莫兰散点图”(Moran scatterplot)，则莫兰指数I即为莫兰散点图回归线的斜率。莫兰散点图分为四个象限，分别对应于观测区域单元与其周围邻居区域的四种局部空间关联形式。其中，第一象限(High-High型)代表高观测值的区域单元被同是高值的区域所包围的空间联系形式；第二象限(Low-High型)代表低观测值的区域单元被高值的区域所包围的空间联系形式；第三象限(High-Low型)代表低观测值的区域单元被同是低值的区域所包围的空间联系形式；第四象限(Low-Low型)代表高观测值的区域单元被低值的区域所包围的空间联系形式。利用stata15.1软件，根据1999年和 2018年房地产风险相关数据分别计算出35个大中城市房地产综合风险局部Moran指数，并进一步得到莫兰散点图，其结果见图1和图2。

图1 35个大中城市局部莫兰散点图(1999年)

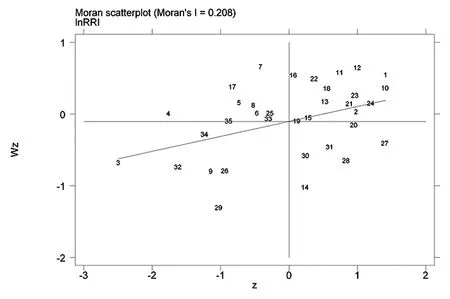
图2 35个大中城市局部莫兰散点图(2018年)

根据图1可知，1999 年位于第一象限的城市主要有广州、深圳、海口等，这些城市表现为房地产风险为高高正自相关关系的集群；位于第二象限的城市主要有南京、杭州、南宁等，这些城市表现为房地产风险为低高负自相关关系的集群；位于第三象限的城市主要有呼和浩特、西安、银川、乌鲁木齐等中西部城市，这些城市表现为房地产风险为低低正自相关关系的集群；第四象限的城市主要有北京、天津、上海等，这些城市表现为房地产风险为高低负自相关关系的集群。根据图2可知，2018年位于第一象限的城市主要有北京、天津、上海、南京、杭州、广州、深圳等，这些城市表现为房地产风险为高高正自相关关系的集群；位于第二象限的城市主要有呼和浩特、沈阳、长春等，这些城市表现为房地产风险为低高负自相关关系的集群；位于第三象限的城市主要有贵阳、兰州、银川等西部城市，这些城市表现为房地产风险为低低正自相关关系的集群；第四象限的城市主要有重庆、成都、西安等，这些城市表现为房地产风险为高低负自相关关系的集群。

通过对比1999年和2018年的局部莫兰指数散点图发现，位于第三象限的城市大多向其他象限转移，即35个大中城市的空间聚集由低低正相关关系集群发展到高高正相关关系集群。这也进一步说明，1999年房地产市场改革之初，房地产风险高高聚集的城市群主要集中在珠三角，随着我国房地产市场的不断发展，到2018年大部分城市的房地产风险水平均有所提升，京津冀和长三角城市群也发展为房地产风险高高聚集的区域。同时与西部城市相比，中东部地区城市的房地产风险提升更加明显。

(三)空间面板模型

一般的空间面板模型形式如下：

(10)

(11)

(12)

模型中各风险指标数据采用前文的计算结果，进行空间统计分析的空间权重矩阵，采用基于人均GDP差值的经济矩阵Wj。其中，各城市经纬度来源于国家地理信息网1:25万全国基础地理数据库，经纬度投影坐标。

1.空间效应检验[14]。由于Moran's I仅可检验是否存在空间相关性，而不能确定空间关系的形式。因此需要通过LM检验来进一步确定是否存在空间误差相关或空间滞后相关。其中，LMerr(Burridge)、LMerr Robust((Bera & Yoon)检验可以确定是否存在空间误差效应，LMsar/lag(Anselin)、LMsar/lag Robust(Bera & Yoon)检验可以确定是否存在空间滞后效应。然后通过LR(Anselin)检验空间杜宾模型是否可退化为空间滞后或空间误差模型。

根据表5，发现LM-err、LM-err R、LM-Lag 和LM-Lag R均通过检验，因此可建立空间滞后模型和空间误差模型。同时，通过LR检验发现，SDM模型可以简化为SAR模型或SEM模型。然后分别对SAR模型和SEM模型进行 Hausman 检验，以进一步确定使用固定效应还是随机效应。

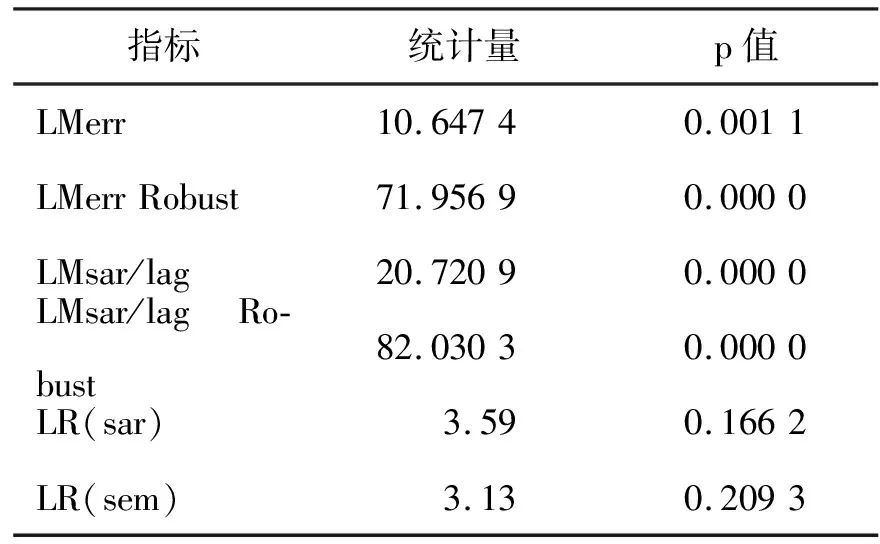
表5 模型空间依赖性检验

根据表6中Hausman检验结果，SAR模型拒绝原假设，SAR固定效应更加有效；SEM模型接受原假设，SEM随机效应模型更加有效。因此本文将选择SAR固定效应模型和SEM随机效应模型进行实证分析。

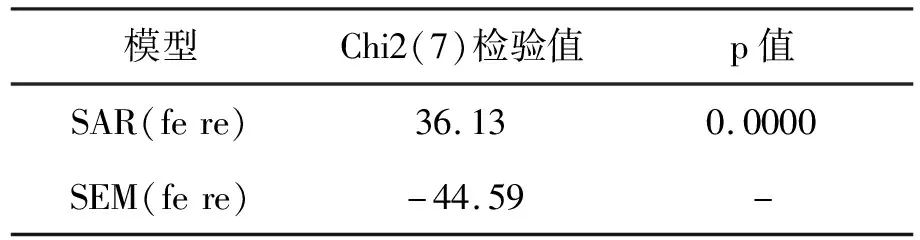
表6 Hausman 检验估计结果

2.参数估计。本文使用STATA15.1软件，采用MLE法对择SAR固定效应模型和SEM随机效应模型的参数进行估计，结果见表7。

由表7的拟合结果可知，两种模型的解释变量房地产环境风险(lnCRI)均没有通过10%的显著性检验，说明环境风险对于城市房地产综合风险的变动影响并不明显。而解释变量开发风险(lnDRI)、融资风险(lnFRI)、价格风险(lnPRI)和库存风险(lnSRI)在两种模型中都表现为显著的正相关，表明房地产开发风险、融资风险、价格风险和库存风险的变动都会对房地产综合风险带来明显的正向影响。此外，SAR模型的人口增长变量(lnn)和SEM模型经济增长变量(lng)均通过10%的显著性检验，并且系数为负值，表明人口增长变动和经济增长变动确实会对房地产风险产生负向影响。如SAR模型显示人口增长速度提高1%，将使房地产风险水平下降0.0489%；SEM模型显示经济增长速度提高1%，将使房地产风险水平下降0.0283%，人口和经济的确为城市房地产的重要基本面和防范风险的长期抓手。由SAR模型的估计结果可知，房地产风险空间滞后项系数显著为正，说明存在显著的空间溢出效应，某一城市的房地产风险会受到邻近城市房地产风险的正向影响，且这种正向溢出效应会在邻近城市间加强。即若本地房地产风险较高，那么会促使邻市房地产风险加强，若本地房地产风险水平较低，那么也会平抑邻市的房地产风险水平。同时，由SEM模型的估计结果可知，空间误差项系数也显著为正，说明本市房地产风险受到相邻地区风险的外溢影响是随机冲击作用的结果。这表明，不包含在模型解释变量中但对房地产风险有影响的遗漏变量(不可观测的随机冲击)存在正的空间相关性。

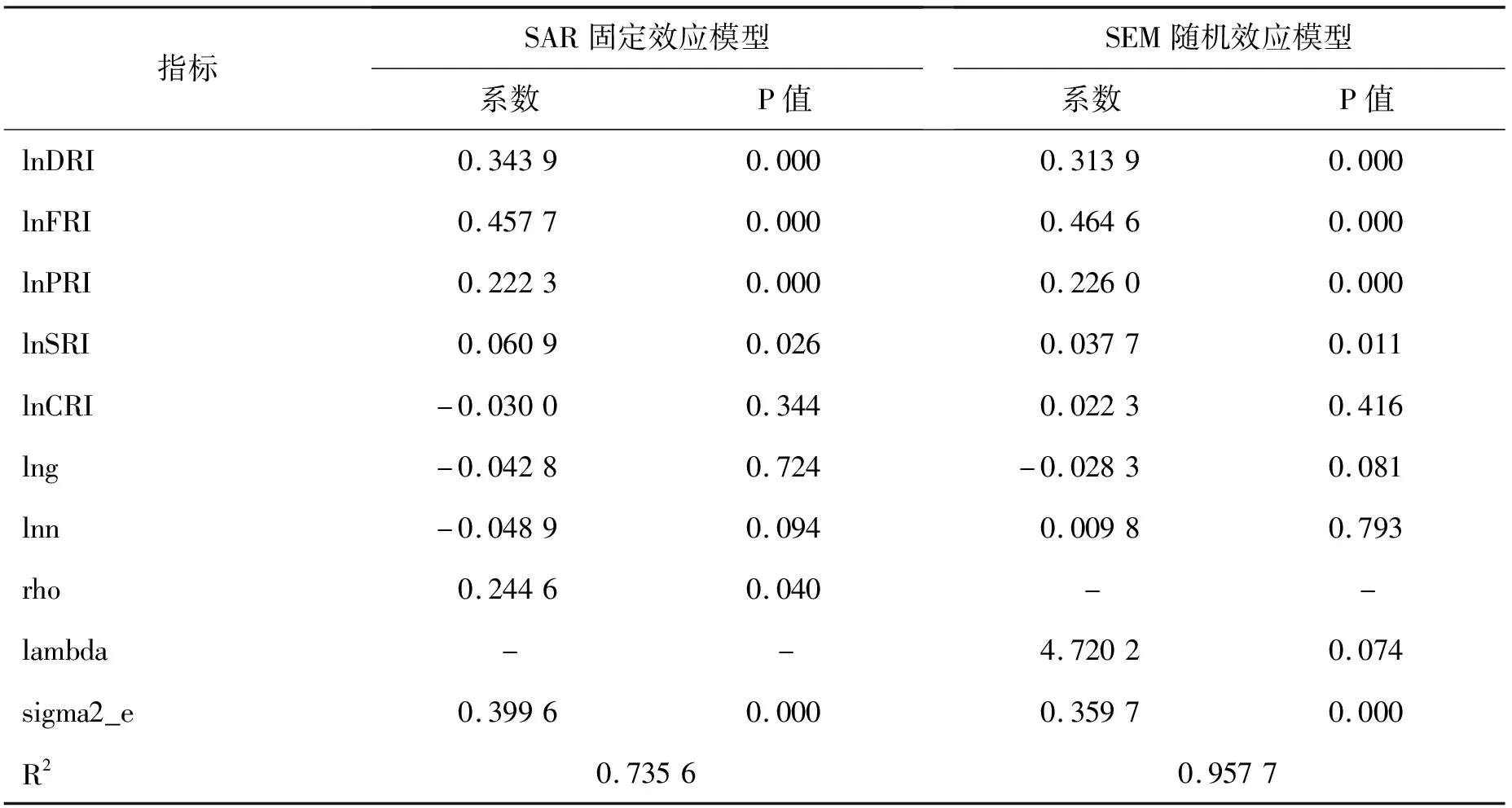
表7 空间面板模型估计结果

四、主要结论和政策启示

本文基于1999—2018 年35个大中城市数据，对大中城市间房地产风险的空间相关性进行了分析，并运用空间面板计量模型，进一步研究了城市房地产风险的空间聚集特征和房地产风险及其影响因素之间的关系。研究结论如下：第一，全局莫兰指数结果表明，经济距离权重矩阵求得的城市房地产风险空间自相关性最为显著，Moran'I指数基本在0.25以上说明空间溢出效应较强，城市房地产风险存在明显的集聚特征。第二，局部莫兰指数结果表明，与1999年相比，2018年的房地产风险高高正相关关系集群的城市明显增加，整体看住房体制改革以来，大中城市的房地产风险整体提高，中东部地区城市的风险增幅明显大于西部地区。第三，空间面板模型实证分析表明，人口增长变动和经济增长变动均会对房地产风险产生负向影响，人口和经济可以作为调控房地产市场风险的基本面因素。而房地产风险空间滞后项系数和空间误差项系数均显著为正。说明城市房地产风险会受到邻近城市房地产风险的正向影响，且这种正向溢出效应会在邻近城市间加强。同时本地房地产风险受到相邻地区风险的正向外溢影响有不包含在模型解释变量中的遗漏变量冲击。

政策启示，针对不同城市的房地产风险结构和程度不同，应继续坚持因地制宜因城施策。新发展格局下，要考虑到不同城市的库存与居民购房需求存在较大差别，完善区域性差别化住房调控政策，把握不同城市不同时期去库存与降杠杆的平衡点，防止房地产市场大起大落。同时，展开跨区域房地产市场风险的协同治理[15]，根据城市群内不同城市间房地产风险空间关联、外溢关系及其差异进行协同联动调控。特别是对京津冀、长三角、珠三角等中心城市，城市群内部经济空间联系紧密、房地产市场发展水平较高，应积极建立房地产调控城市间协调机制，加强城市群内中心城市与周边城市房地产调控部门间的沟通与协作，协调配合好各城市房地产调控政策的选择实施，及时防止中心城市房地产风险向周边城市扩散蔓延。从长期看，则通过多主体供给、多渠道保障，加快各项基础设施建设，平衡好稳增长和防风险的关系，把握好节奏和力度，稳妥实施房地产市场平稳健康发展的长效机制方案。