多密度自适应确定DBSCAN算法参数的算法研究
万 佳,胡大裟,蒋玉明
1.四川大学 计算机学院,成都 610065
2.四川省大数据分析与融合应用技术工程实验室,成都 610065
数据挖掘指从数据中发现知识,其目的是从大量数据中发现有价值的隐含信息。目前,随着互联网技术的快速发展,数据呈爆炸式增长,人们迎来了大数据时代。在大数据的众多方向中,聚类分析是数据挖掘重要的研究方向之一。聚类分析研究的是无监督模式识别问题,它在图像分析、遥感、生物信息学和文本分析等领域都有应用[1]。聚类主要用于将数据分组为有用的簇,使得每个簇内的对象相似度高,簇间相似度低。聚类算法在传统上可以分为基于划分的方法、基于层次的方法、基于模型的方法、基于密度的方法和基于网格的方法。
基于划分的方法中,k-means[2]算法是经典的聚类算法,该算法经过多次迭代找到最佳聚类中心,再根据样本点到聚类中心的距离对样本进行划分。由于该算法是将样本分配到最近的簇中,因此不能发现任意形状的簇,并且容易陷入局部最优,导致聚类结果不稳定。
在基于密度的聚类中,DBSCAN[3]是一种经典的聚类算法,可以将高密度区域划分为簇,并在含有噪声的数据集中实现任意形状的聚类。但是该算法存在两方面的问题,首先需要在无先验知识的情况下人工指定Eps(Epsilon)和MinPts(Minimum Points)这两个参数,且参数选取对聚类结果影响很大,另外,DBSCAN算法在密度分布不均匀的数据集上,聚类效果不佳。许多学者对DBSCAN算法进行了各种研究和改进。文献[4]提出了VDBSCAN算法,它使用k-dist图对不同密度选择合适的参数,找到具有不同密度的簇。文献[5]提出了一种基于改进的元启发算法MVO(multi-verse optimizer)的参数确定方法,该方法可以快速找到DBSCAN算法的最高聚类精度以及精度最高的Eps对应的区间。Kim等[6]提出AA-DBSCAN算法,基于四叉树的结构来定义密度层次,实现不均匀密度数据集的聚类。Bryant等[7]提出RNN-DBSCAN算法,该算法使用逆近邻计数作为密度的估计,改进了密度分布差异大的数据集的聚类效果。文献[8]提出一种新的基于相似性度量的改进DBSCAN算法,更好地刻画了数据集的分布特征。文献[9]提出了一种自适应选择DBSCAN参数的KLS-DBSCAN算法,该算法利用数据自身的分布特点找出合理的参数范围,再通过寻找聚类内部度量最大值的方法确定最佳参数。李文杰[10]等提出KANN-DBSCAN算法,该算法能够实现聚类过程的全自动化并且能够选择合理的参数,得到高准确度的聚类结果,但在密度分布差异大的数据集上效果较差。
鉴于此,本文提出了一种多密度自适应确定DBSCAN算法参数的MDA-DBSCAN算法,该算法通过去噪衰减后的数据集自身分布特性生成初始候选Eps和MinPts参数列表,并在簇类结果趋于稳定时得到初始密度阈值,之后对该密度阈值条件下识别出的噪声数据进行相同操作,得到新密度阈值,最终合并不同密度阈值下的聚类结果,整个聚类过程无需人为干预,且聚类效果在密度分布差异大的数据集上得到了明显的提升。
1 相关定义
DBSCAN算法是1996年由Ester[11]提出的基于密度的空间聚类算法,为了准确描述该算法,给出以下定义。
定义1(Eps邻域)一个数据对象p,p的邻域NEps(p)定义为以p为中心,以Eps为半径的区域内,即:
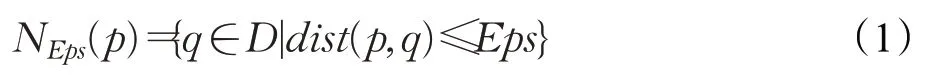
其中,D为数据集;dist(p,q)表示D中两个数据对象p和q之间的距离;NEps(p)包含了数据集D中与对象p距离不大于Eps的所有对象。
定义2(核心点和边界点)对于数据对象p∈D,设定MinPts阈值,若|NEps(p)|≥MinPts,则称p为核心点;非核心点但在某核心点的Eps邻域内的对象称为边界点。
定义3(直接密度可达)若p在点q的Eps邻域内,即p∈NEps(q),且对象q是核心点,即|NEps(q)|≥MinPts,则称对象p是从对象q密度直达的。
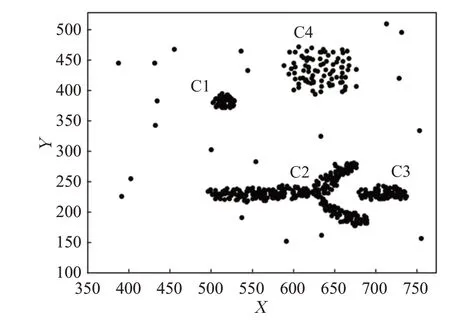
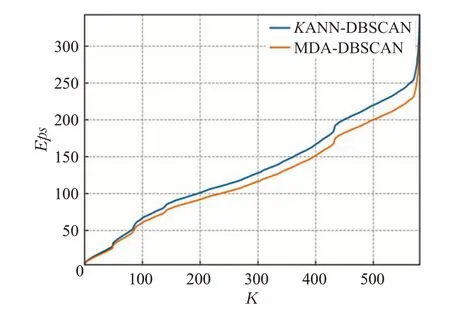
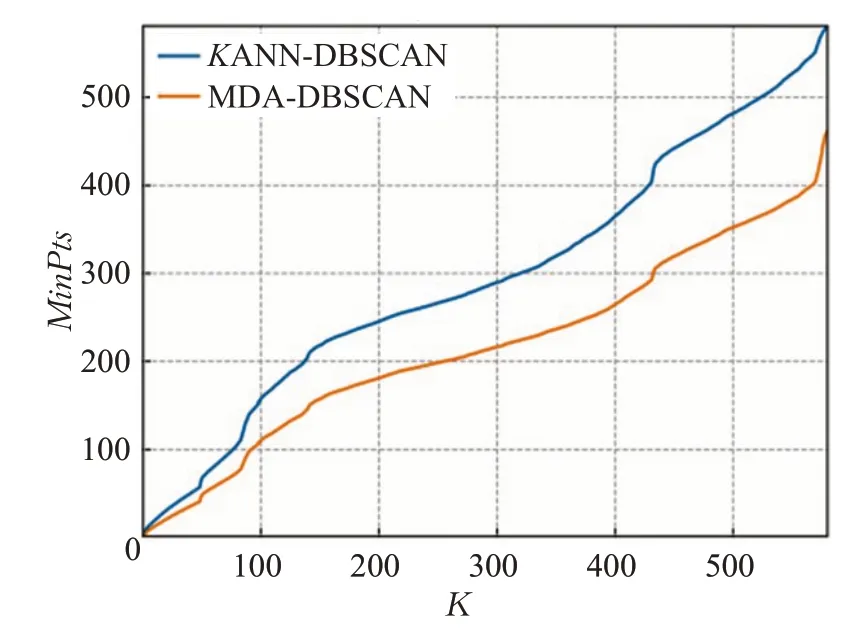
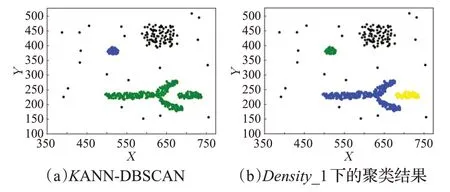
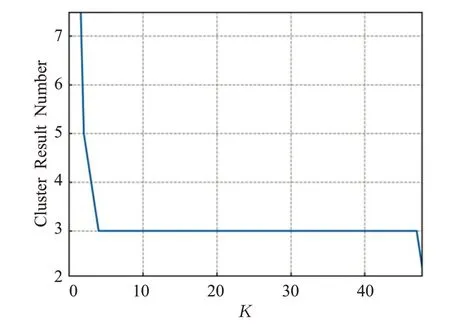
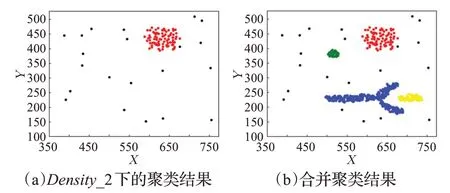
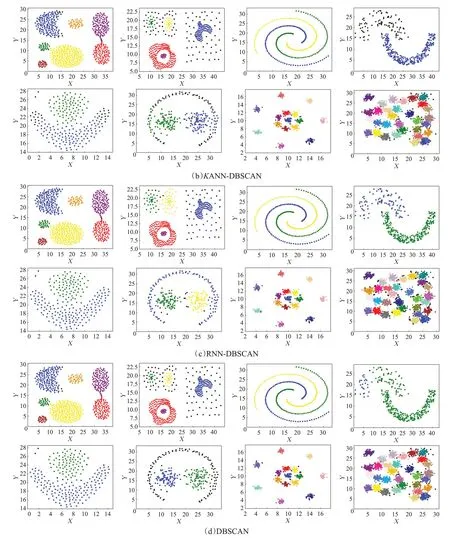
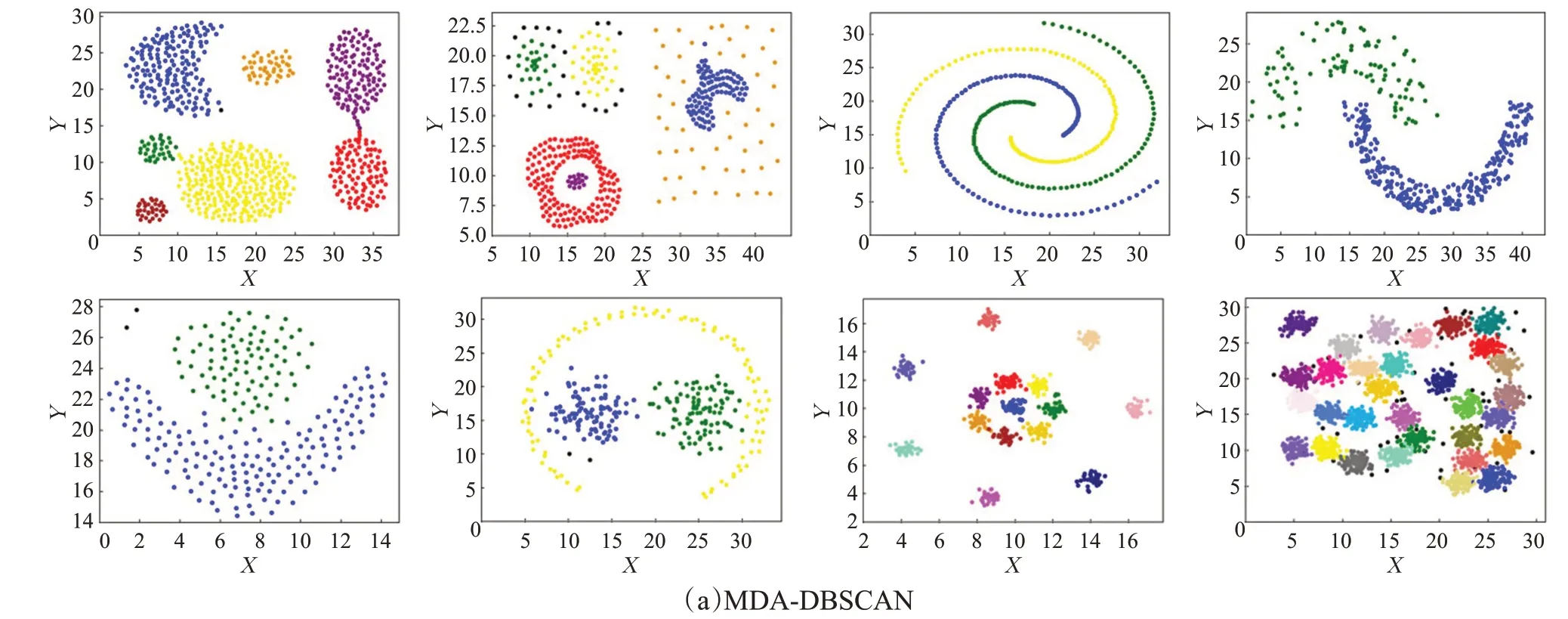
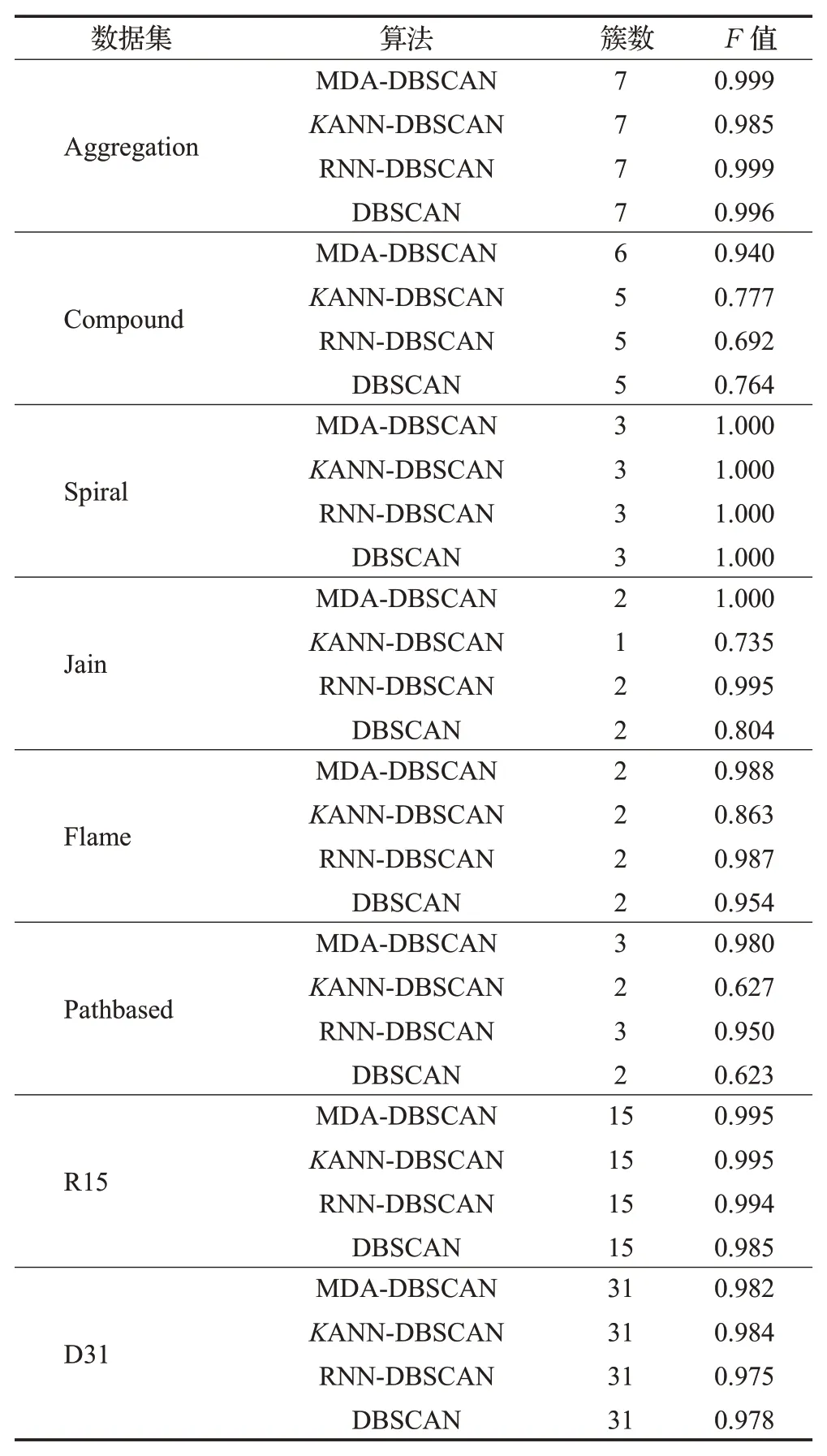
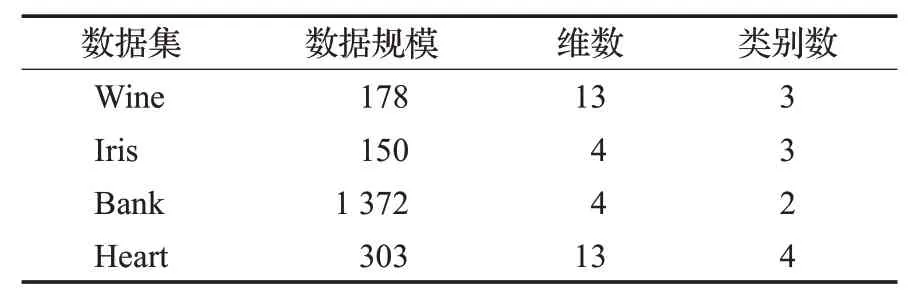
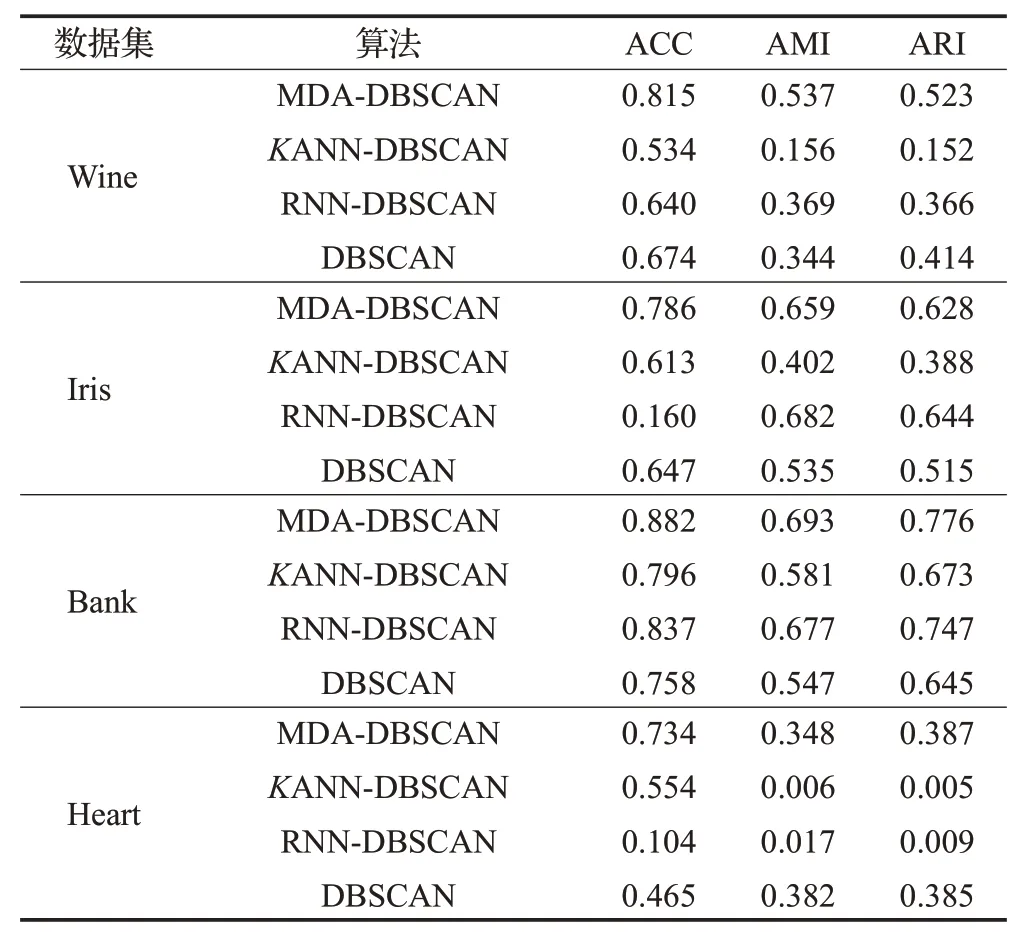
定义4(密度可达)给定数据集D,当存在对象p1,p2,…,pn∈D,对于pi∈D(0 定义5(密度相连)若存在对象r∈D,使得对象p和q是从r密度可达的,那么称对象p和q密度相连。密度相连是对称的。 定义6(簇和噪声)由任意一个核心点对象开始,从该对象密度可达的所有对象构成一个簇,不属于任何簇的对象为噪声。 定义7(密度阈值)给定(Eps,MinPts),以Eps为半径的圆内存在MinPts个数据点,即: 其中,Density为密度阈值[10]。 KANN-DBSCAN算法利用数据集自身的空间分布特性,基于K-平均最近邻算法和数学期望法生成Eps和MinPts参数列表。该算法存在两个问题:(1)K-平均最近邻得到的平均值容易受到噪声数据的影响从而导致生成的参数列表存在误差;(2)由于DBSCAN算法自身的不足,KANN-DBSCAN算法对密度分布差异较大的数据集进行聚类时存在一定的误差,导致聚类结果簇数和数据集类别数不一致的情况出现[10]。为了更好地阐述和解决问题,本文假设密度分布差异大的数据集中密集分布的数据比稀疏分布的数据多。 针对问题(1),在密集分布的数据较多的情况下,KANN-DBSCAN算法得到的参数会偏向密集分布的簇进行聚类,在聚类过程中,密集数据的参数取值会受到噪声数据的影响,即在计算数据点之间的距离时,噪声点也会参与,涉及到该点的距离会偏大,这使得之后计算出的平均值也偏大,最后导致自适应生成的Eps参数列表的值偏大,所以在密度分布差异大的数据集中,该算法自适应选取的参数不够准确。Eps的值偏大,可能导致不同簇类之间被合并,所以为了在密度分布差异大的数据集中选取合适的参数,需要对K-平均最近邻算法得到的Eps参数列表进行二次处理,使其更符合数据的自身分布特性。处理了Eps后,密度阈值会发生改变,为了使其稳定,同时处理数学期望法生成的MinPts列表。本文通过给K-平均最近邻算法和数学期望法增设自衰减项,使得生成的Eps和MinPts列表的值同时减小,从而减少噪声数据对参数自适应生成的影响,优化密度阈值的生成。 针对问题(2),KANN-DBSCAN算法的密度阈值是作用于全局的,这使得稀疏数据形成的簇被识别为噪声,为了正确地识别簇,本文引入多密度阈值Density_i参数概念,如式(3): 其中,Epsi和MinPtsi为第i次自适应选取的参数,Density_1为第1次自适应选取的参数生成的初始密度阈值,Density_2为在Density_1下聚类产生的噪声数据的密度阈值,Density_3为在Density_2下聚类产生的噪声数据的密度阈值,以此类推,直到噪声数据数量或生成的密度阈值低于一定程度为止,最后将所有密度阈值下的聚类结果进行合并。 MDA-DBSCAN算法的关键是能够在密度分布差异大的数据集上自适应确定具有不同密度的簇的最优密度阈值。本文提出利用数据分布特性,基于自衰减项的K-平均最近邻算法(K-average nearest neighbor with attenuation term)和自衰减数学期望法生成密度阈值。 为了方便描述该算法,以图1数据集为例,该数据集是一个含有4种类别共582个对象的二维数据集。数据集中有三个密集的簇C1、C2和C3,包含477个对象,一个稀疏的簇C4,包含85个对象,以及一些噪声点,包含20个对象。其中C1、C2和C3在同一密度阈值下,且C2和C3簇间间距较小,C4属于另一个密度阈值。综上,该数据集的特点包括:(1)存在密度分布差异大的簇;(2)存在簇间间距小的簇;(3)含有一定数量的噪声点。该数据集的分布与本文要解决的两个问题一致。下文以该数据集为例进行具体分析。 图1 数据集散点图(N=582,C=4)Fig.1 Data point diagram(N=582,C=4) 2.2.1 自衰减生成Eps参数列表 采用基于自衰减项的K-平均最近邻法生成Eps列表,其中K-平均最近邻法是平均最近邻法的拓展,该算法是计算数据集D中每个数据点与其第K个最近的数据点之间的K-最近邻距离,并对所有数据点的K-最近邻距离求平均值,得到数据集的K-平均最近邻距离。生成参数列表的具体步骤如下: 步骤1计算数据集D中每个点到其他点的欧氏距离,形成距离分布矩阵Distn×n,如式(4): 其中,n是D中的数据点个数;dist(i,j)是数据集中点i和点j之间的距离;Distn×n是n×n的实对称矩阵。 步骤2将Distn×n的每一行元素进行升序排序。 步骤3对排序后矩阵Distn×n的第K(1≤K≤n)列求平均值,得到----DK,减去自衰减项后,将其作为候选Eps参数。如式(5): 其中,λ是自衰减系数,0≤λ≤1,本文λ取值为0.3。对所有的K值计算完毕后,得到Eps参数列表,如式(6): 图2为图1数据集分别在KANN-DBSCAN算法和MDA-DBSCAN算法下生成的Eps参数列表对比曲线,可见本文提出的算法可以平稳降低Eps参数的值,从而减少数据噪声的影响,以得到更优的Eps参数列表。 图2 Eps参数列表对比图Fig.2 Comparison diagram of Eps parameter list 2.2.2 自衰减生成MinPts参数列表 采用基于自衰减项的数学期望法生成MinPts列表。如式(7): 其中,λ是自衰减系数,0≤λ≤1,n为数据集中的对象总数,Pi是第i个对象的Eps邻域内邻域对象数量。对所有的K值计算完毕后,得到MinPts参数列表,如式(8): 图3为图1数据集分别在KANN-DBSCAN算法和MDA-DBSCAN算法下生成的MinPts参数列表对比曲线。 图3 MinPts参数列表对比图Fig.3 Comparison diagram of MinPts parameter list 2.2.3 多密度自适应确定最优参数 对于图1数据集,KANN-DBSCAN算法根据数据自身分布特性得到的Eps参数会受到噪声数据的影响而偏大,这可能导致簇间间距较小的不同簇类被识别为一个簇,比如簇C2和簇C3,另外,由于参数的全局性,稀疏簇C4会被识别为噪声,如图4(a)所示。本文设计的算法能够减少噪声数据的影响,得到优化后的初始密度阈值Density_1,使得簇C2和簇C3能正确地被识别为不同的簇。具体做法如下文。 图4 密度阈值的优化Fig.4 Optimization of density threshold 首先通过自衰减改进后的方法得到Eps和MinPts参数列表,选取第K个参数对(1≤K≤n),即(EpsK,MinPtsK),输入DBSCAN算法,对数据集进行聚类分析,得到聚类结果簇数与K值的关系如图5所示。 图5 聚类结果簇数与K值的关系图Fig.5 Relational diagram of K value and number of clusters of clustering results 当聚类结果的簇数趋于稳定时通过K值反向选取最优参数。本文对结果趋于稳定进行了重新定义,X表示聚类结果簇数相同的连续次数:(1)当连续X(本文设定初始值为5)次相同时,认为聚类结果趋于稳定,得到稳定区间(第一个即可),记该簇数为最优簇数。若聚类结果不存在连续X次相同的簇数,则寻找连续X-1次相同的簇数;(2)若(1)中连续三次相同的簇数都找不到,则改为寻找簇数波动范围在1内的稳定区间。 找到稳定区间后,得到区间端点startK和endK,本文根据识别噪声程度的需求来选取稳定区间中的K值,通过设置噪声等级level来实现,设有三个噪声等级:less(少噪声)、normal(正常噪声)和more(多噪声,默认值)。K值选取如式(9)所示。一般在密度分布均匀的数据集上设置噪声等级为less,在密度分布差异大的数据集上设置噪声等级为more,其余情况设置为normal。 利用上述定义对图1数据集进行分析,如图5所示,当K=4时,进入稳定区间,直到K=47结束,因此选取K值为4,其对应的Eps1=7.813,MinPts1=8。将该最优参数输入DBSCAN算法,得到Density_1下的聚类结果如图4(b)所示,与图4(a)KANN-DBSCAN算法的聚类结果比较,本文算法能够正确地识别簇C2和簇C3,将它们归为不同簇类,可见本文算法处理噪声数据的有效性。 之后抽取Density_1下聚类后的噪声数据,即稀疏簇C4和噪声点,共105个对象,通过同样的方式自适应确定其最优参数,得到新密度阈值Density_2,此时Eps2=12.267,MinPts2=3,Density_2下噪声数据的聚类结果如图6(a),然后抽取Density_2下聚类后的噪声数据,共21个对象,不满足本文设定的最小噪声数量(50),结束聚类,最后将Density_1和Density_2下的聚类结果合并得到如图6(b)所示结果,聚类结果簇数与数据集标识类别一致,可见本文算法处理密度分布差异大的数据集的有效性。 图6 基于MDA-DBSCAN的聚类结果Fig.6 Clustering results based on MDA-DBSCAN MDA-DBSCAN算法采用Python3.7实现,实验环境为64位的Windows10系统,实验运行在i7-10710U,CPU为1.1 GHz,内存16 GB的笔记本上。为了进一步验证本文算法的有效性和先进性,在人工数据集和UCI数据集上进行了聚类分析,将本文算法得到的结果与DBSCAN、KANN-DBSCAN、RNN-DBSCAN算法进行比较。其中,本文算法需要提供的参数:多密度阈值Density_i(Di)。DBSCAN算法和KANN-DBSCAN算法都需要设定两个参数:半径Eps和最小样本数MinPts。RNN-DBSCAN算法需要设定一个参数:点的邻居数K。表1显示了四种算法在人工数据集上的较优参数的设置。 表1 人工数据集上的参数设置Table 1 Parameter settings on artificial data sets 本文选用8组人工数据集进行实验,包括密度分布均匀和不均匀的数据集,并用F值[12]对结果进行分析,F值综合了准确率和召回率,取值范围在[0,1],越接近1表示聚类效果越好。数据集的详细信息见表2。 表2 人工数据集Table 2 Artificial datasets 图7为本文算法与其他算法在不同人工数据集上的聚类结果,可见MDA-DBSCAN算法不仅在密度分布均匀的数据集上有效,而且在密度分布差异大的数据集上也有很好的聚类效果。 图7 (续) 图7 聚类结果对比Fig.7 Comparison of clustering results 从聚类结果簇数来看,MDA-DBSCAN算法最为准确,即聚类结果簇数与数据集类别数一致。从F值评价指标来看,在密度分布均匀的数据集(Aggregation、Spiral、Flame、R15和D31)上,MDA-DBSCAN算法与其他算法的差异不大,都有较优的结果,但在密度分布差异大的数据集(Compound、Jain和Pathbased)上,MDADBSCAN算法的优势明显,具有更高的准确性。表3是几种算法的聚类结果簇数和指标评价。 表3 聚类结果簇数和指标评价Table 3 Cluster number of clustering results and index evaluation 为了验证MDA-DBSCAN算法在真实数据集上的性能,对UCI数据集进行聚类分析,并采用准确率(ACC)[13]、互信息(AMI)[14]和调整兰德系数(ARI)[15]作为评价指标,其中ACC的取值范围在[0,1],AMI和ARI的取值范围在[-1,1],值越接近1说明与真实聚类结果越符合。数据集详细信息如表4所示。 表4 UCI数据集Table 4 UCI datasets 真实数据集聚类指标如表5所示,可以看出本文算法克服了传统算法的人工选取参数的主观性,并在高维数据集上有良好的表现。KANN-DBSCAN算法虽然在二维的人工数据集上有较好的表现,但是在高维UCI数据集上表现一般,因为在分布不均的高维UCI数据集上很难进入连续三次相同的簇数稳定区间,导致聚类结果出现较大误差。本文算法在利用数据集自身分布特性确定密度阈值前对数据集进行了去噪衰减,减少了噪声数据的影响,并且重新制定了稳定区间的选取策略,能够得到更符合数据特性的密度阈值,并进行多次密度阈值计算,合并所有聚类结果,从而提升聚类效果。 表5 聚类指标对比Table 5 Comparison of clustering index DBSCAN算法可以有效识别噪声并实现任意形状的聚类,但是该算法对参数的选取敏感,取值不当会导致聚类效果不佳,且由于参数的全局性,该算法在密度分布步不均匀的数据集上不能正确地识别簇。本文在KANN-DBSCAN算法的基础上,引入了去噪衰减、多密度阈值以及合并聚类的概念,用例子演示了算法具体实现步骤,通过自衰减项与平均最近邻和数学期望法结合生成改进的参数列表,找到最优初始密度阈值,得到聚类结果和噪声数据,对噪声数据进行相同操作直到其数量或密度阈值不满足条件为止,最后将所有密度阈值下的聚类结果进行合并。实验表明,本文算法可以自适应确定具有不同密度的簇的最优密度阈值,在密度分布不均匀的数据集上有很好的聚类结果,但算法时间复杂度较高,如何有效降低算法时间复杂度是以后工作的重点。
2 多密度自适应确定DBSCAN算法参数
2.1 基本思想

2.2 算法设计
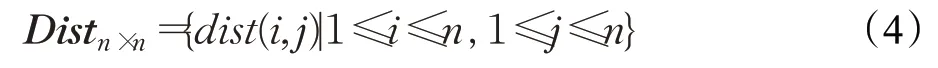

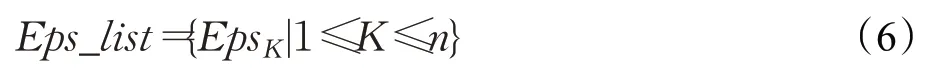
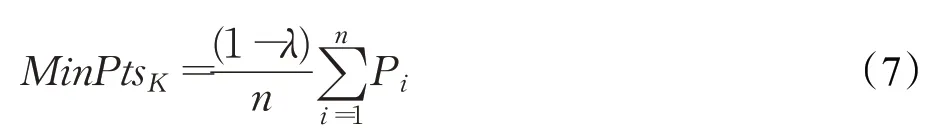

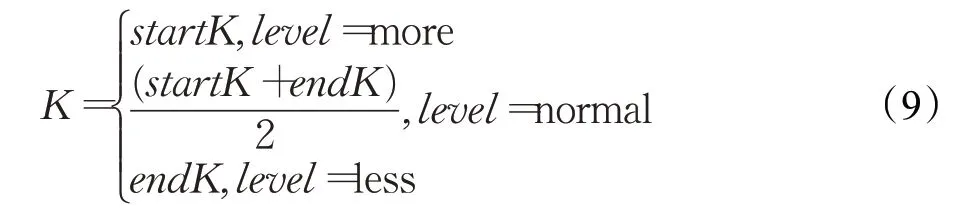
3 实验与结果分析

3.1 人工数据集
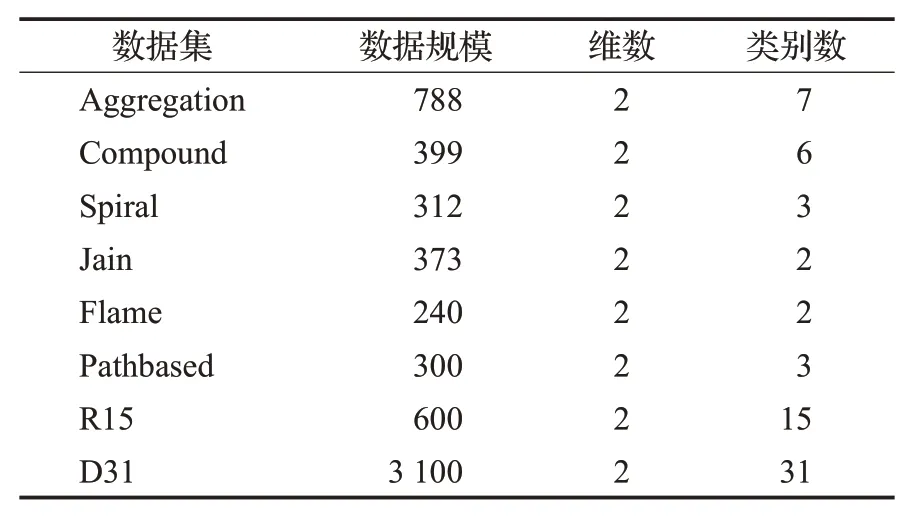
3.2 UCI数据集
4 结束语

