基于深度随机森林的新型组合分类算法*

任志伟，王玉德，陈 婷

（曲阜师范大学，山东 曲阜 273165）

0 引言

机器学习作为一个重要的分支在很多领域，如医疗、环境、地理等领域，得到了快速的发展[1-3]。为了利用诸如支持向量机（Support Vector Machine，SVM）的单分类器实现样本的分类，孔德峰通过训练多种常规单分类器模型对乳腺癌肿瘤进行分类研究，得出的K 最邻近分类算法（K-NearestNeighbor，KNN）模型具有较好的分类效果[4]。刘蕾通过采用一种logistic 方程归一化后的线性回归分类方法，得出的基于两个特征的逻辑回归模型具有较好的性能[5]。为了利用多个单分类器组合的方式进一步提升分类性能，张晓等人利用SVM、反向传递（Back Propagation，BP）神经网络和AdaBoost 算法的加权投票的方式来弥补单分类器性能不足的问题，实现了更高的目标识别准确度[6]。李晓丽等人通过融合SVM、径向基函数（Radial Basis Function，RBF）神经网络和贝叶斯网络，实现更好的科普知识文本分类效果[7]。但是目前大多数单分类器融合方法不能很好地解决不同数据集下单个分类器最优性能的问题，使得算法的鲁棒性较差。

鉴于上述问题，本文提出了基于深度随机森林的新型组合分类算法，训练建立不同深度随机森林组合的模型，以实现在不同数据集下均有较好性能的分类算法。

1 数学基础

1.1 决策树

决策树是基于树结构进行决策的，可以将其认为是if-then 规则的集合。一颗决策树包含一个根节点、若干内部节点和若干叶节点。内部节点作为划分节点，叶节点对应决策结果。用决策树进行分类，是从根节点开始，利用划分准则将实例分配到其子节点，若该节点仍为划分节点，则继续进行判断与分配，直至将全部样本分到叶节点的类中，这一训练过程中只涉及少量的参数调整[8]。常用的决策树划分准则有第三代迭代二叉树（Iterative Dichotomiser 3，ID3）、ID3的改进算法（C4.5）和分类回归树（Classification and Regression Tree，CART）等算法[9]。基于CART 算法的决策树生成的二叉树是以基尼指数（Gini's diversity index）作为划分准则。基尼指数代表了特征数据的纯度情况与信息增益（ID3）或信息增益比（C4.5）相反，基尼指数越小代表特征数据的纯度越高，把基尼指数最小的一个特征作为当前节点的划分特征[10-12]。基尼指数的计算公式为：

式中：D为样本总数；K为类别数；Ck为样本中属于K类的个数。

基于特征A划分后的基尼指数计算公式为：

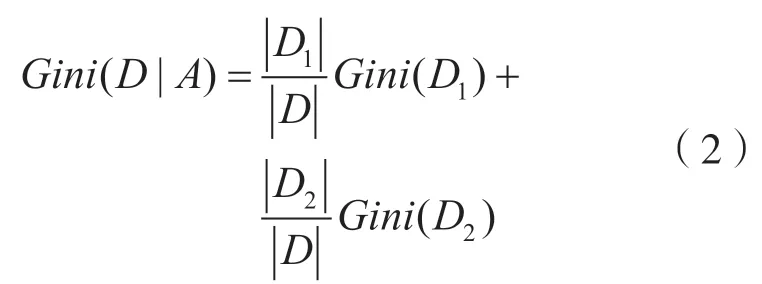
式中：D1，D2为样本D根据特征A所划分的两个部分。

1.2 随机森林

随机森林是Breiman 在2001 年提出的一种组合分割算法，其本质是包含了若干个随机决策树，将每一个随机决策树的结果组合起来决定待分类样本的归属类别[13]。当输入待测样本之后，随机森林会根据每个随机决策树的输出结果进行统计，将最多划分的类别作为该输入样本最终确定的划分类别。随机森林较其它分类器具有很好的泛化能力并且不需要复杂的参数，在小样本背景下具有很好的性能[14]。同时随机森林在较高准确度的前提下具有很好的可解释性，能更好地避免过拟合且具有很强的鲁棒性[15-16]。

随机森林具有样本随机和特征随机的特点。假设有N个样本，随机有放回的从这N个样本中选取n个样本作为训练集（这种方法称为bootstrap sample），即样本随机，同时从样本特征（假设有M个特征）中随机选取k个属性（k＜M），从这k个特征中选取最佳分割属性作为节点建立随机决策树，即特征随机[17-19]。重复以上两个随机步骤m次就可以得到m颗独立的随机决策树，这样就建立了深度为m的随机森林，然后依据每棵树的投票情况来确定样本所属类别。

1.3 模型评价标准

分类器性能评价指标主要有：混淆矩阵（confusion matrix），准确度（accuracy），灵敏度（sensitivity），特异性（specificity）。

混淆矩阵（confusion matrix）用来记录一个分类器所有的分类情况，这里以二分类说明，如表1所示。

表1 二分类混淆矩阵

实验二分类的混淆矩阵，TP（True Positive）代表真阳性，NTP即实际为正样本预测为正样本的个数；FP（False Positive）代表假阳性，NFP即实际为负样本预测为正样本的个数；FN（False Negative）代表假阴性，NFN即实际为正样本预测为负样本的个数；TN（True Negative）代表真阴性，NTN即实际为负样本预测为负样本的个数。

准确度（Accuracy）是对分类器的整体分类预测能力的评价，计算方式为：

准确度越高代表分类器的分类预测能力越好，正确分类的数量占整个样本数量的比例也就越高。

灵敏度（sensitivity）代表了模型对正样本预测的准确度，指标均越高越好。特异性（specificity）代表了模型对负样本的预测精度，指标均越高越好，如式（4）、式（5）所示。

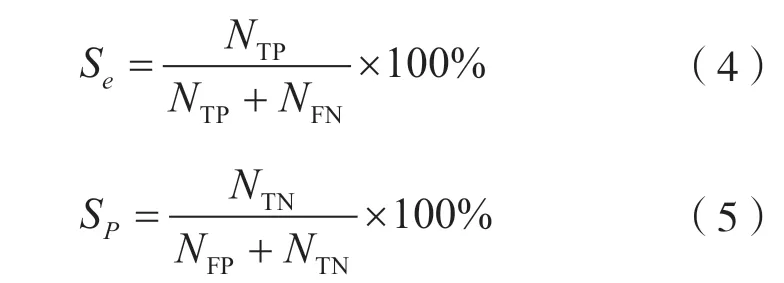
式中：Se代表灵敏度；Sp代表特异性。

2 算法实现步骤

组合分类算法的实现主要有以下几个步骤：

（1）样本数据的预处理，数据归一化；

（2）设定随机森林模型的深度范围从50 到400，间隔为5，重复训练5 次并综合每个深度模型的结果；

（3）根据步骤（2）的训练和综合结果，组合前5 个平均准确度最高（最优）的随机森林模型的综合结果，通过投票确定最终的分类器结果；

（4）对模型进行十折交叉检验，评价最优组合模型的分类效果；

（5）与常规的分类算法进行实验对比，检验论文提出算法的有效性。

算法流程如图1 所示。

图1 算法实现过程

3 实验与结果分析

3.1 实验数据

实验使用的平台为Matlab2016b，实验数据为威斯康辛州（诊断）乳腺癌数据集、无线定位数据集和汽车评估数据集。该乳腺癌数据集共有683 个样本，本文抽取其中100 个数据用于最终的模型验证），如表2 所示。每个样本具有9 个特征。“-1”代表良性，实验中将“-1”类定义为正类；“1”代表恶性，实验中将“1”类定义为负类。该样本中良性与恶性所占比例如图2 所示。

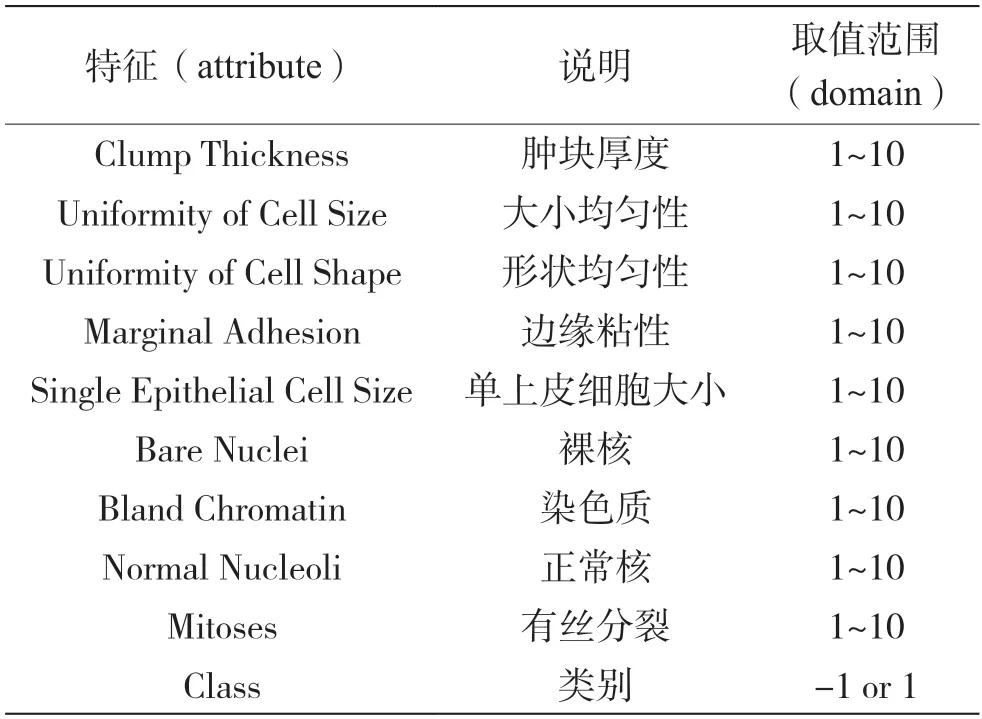
表2 乳腺癌数据集特征与取值范围

图2 乳腺癌数据集训练样本的占比

无线定位数据集中包含了2 000 个样本，本文抽取其中400 个样本用于最终的模型验证，每个样本包含7 个特征，表示用户端分别与7 个不同WiFi发射端之间的信号强度大小，分类结果为用户端所在楼层的ID，如表3 所示。该样本中类别所占比例如图3 所示。

图3 无线定位数据集训练样本的占比

表3 无线定位数据集特征与取值范围

汽车评估数据集包含1 728 个样本，本文抽取其中500 个用于最终的模型验证，每个样本具有6个特征。分类结果为“unacc”和“acc”如表4 所示。该样本中类别所占比例如图4 所示。

表4 汽车评估数据集特征与取值范围

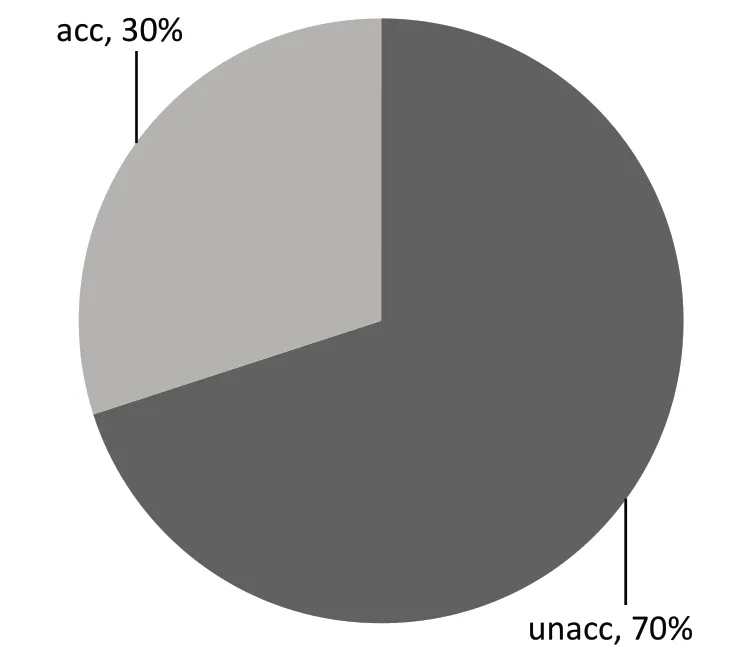
图4 汽车评估数据集训练样本的占比

对数据集进行标准化处理，将每个样本的特征值映射到[0,1]之间，从而去除单位限制，将原数据转为无量纲的纯数值，计算方式为：

式中：Xmin为序列的最小值；Xmax为序列的最大值。

3.2 实验过程与结果分析

在乳腺癌数据集上进行实验。实验中，模型深度范围50～400，间隔为5，训练得到不同随机森林模型71 个。通过十折交叉检验获取这71 个模型在训练样本上的准确度，然后重复5 次并计算每个模型的平均准确度，同时将这5 次的结果进行投票生成这71 个单随机森林模型的综合结果。由于当平均准确度接近时，组合更多的模型并不能提高最终组合算法的准确度，同时考虑到参与投票的单模型的个数应为奇数，因此本实验选取平均准确度最高的前5 个单模型参与组合。根据平均准确度最高的前5 个单随机森林模型的综合结果，再次进行投票确定最终的分类结果。如图5 所示，平均准确度最高的前5 个随机森林模型的深度分别为295、325、360、365 和380。

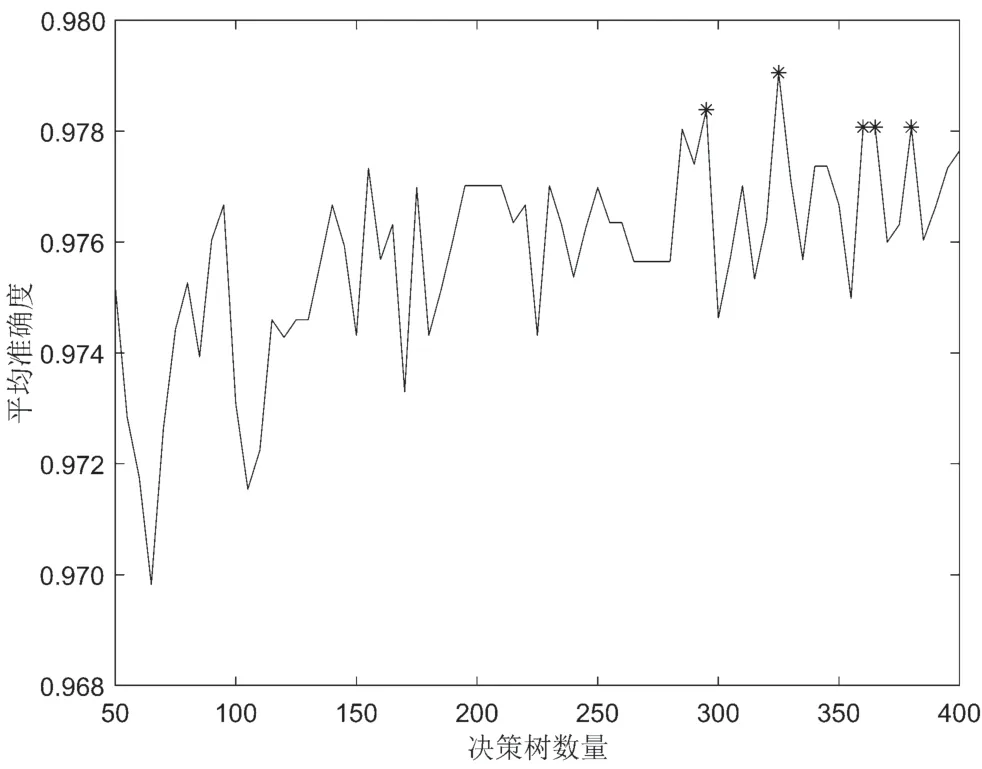
图5 不同深度的随机森林模型准确度

将这5 个不同深度的随机森林模型单独进行全部样本的预测，然后统计这5 个随机森林模型对每一个样本的预测情况，预测结果达到半数以上则为组合模型对样本的最终预测结果，即组合模型对样本x的预测结果运用投票规则C(x)可以表示为：

式中：y-1为正类；y1为负类；i为对正类的投票数。

实验中KNN 表示最近邻算法模型；以SVM 表示支持向量机模型；以TREE 表示决策树模型；以FOREST 表示最高性能的单随机森林模型；以C-FOREST 表示本文提出的算法模型。

分析图6、图7、图8、图9、图10，得出各分类器的灵敏度（sensitivity）、特异性（specificity）和准确度（accuracy），如表5 所示。

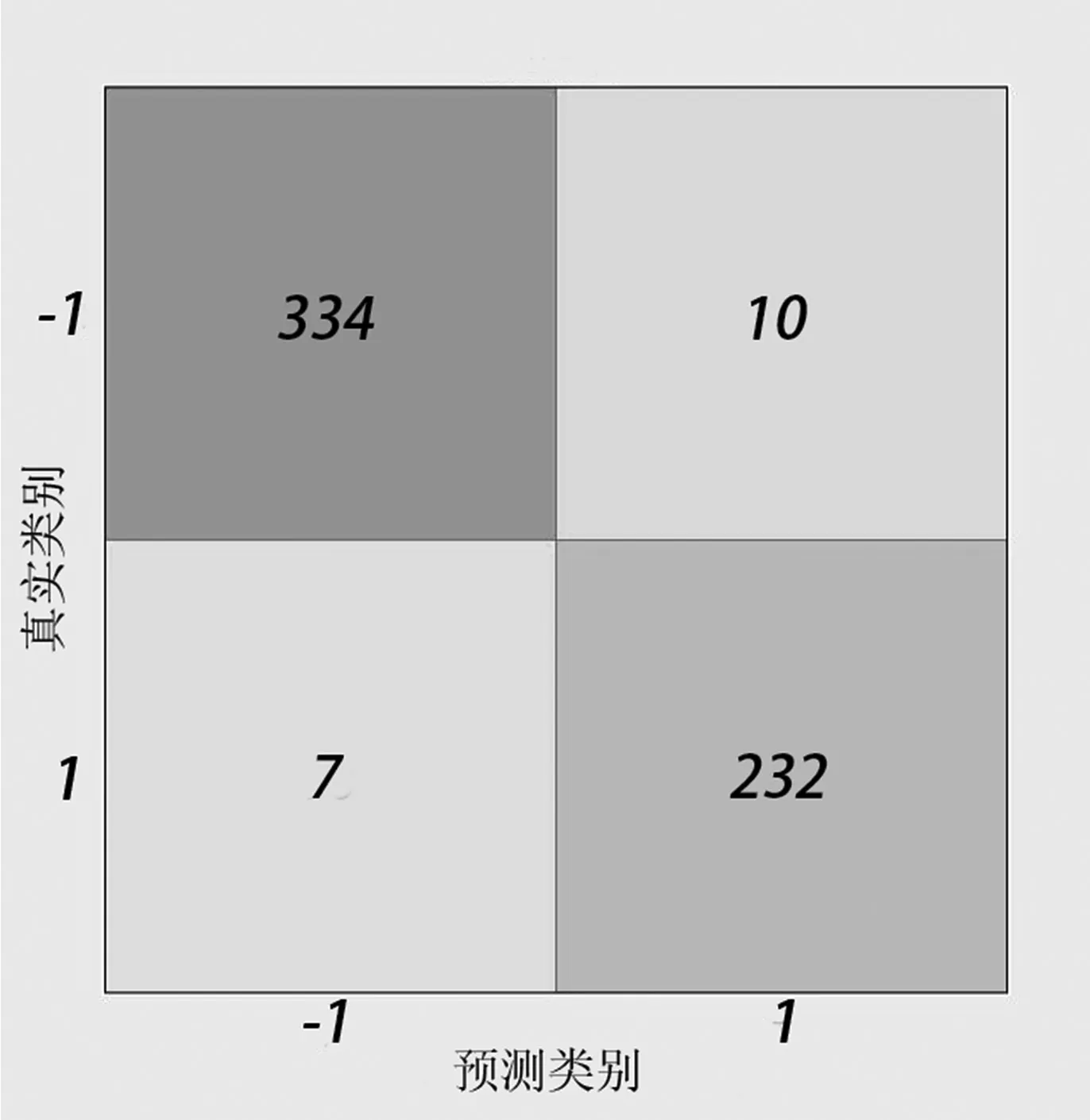
图6 KNN 混淆矩阵

图7 SVM 混淆矩阵

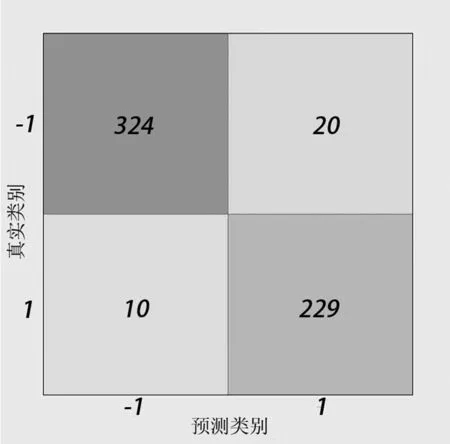
图8 TREE 混淆矩阵

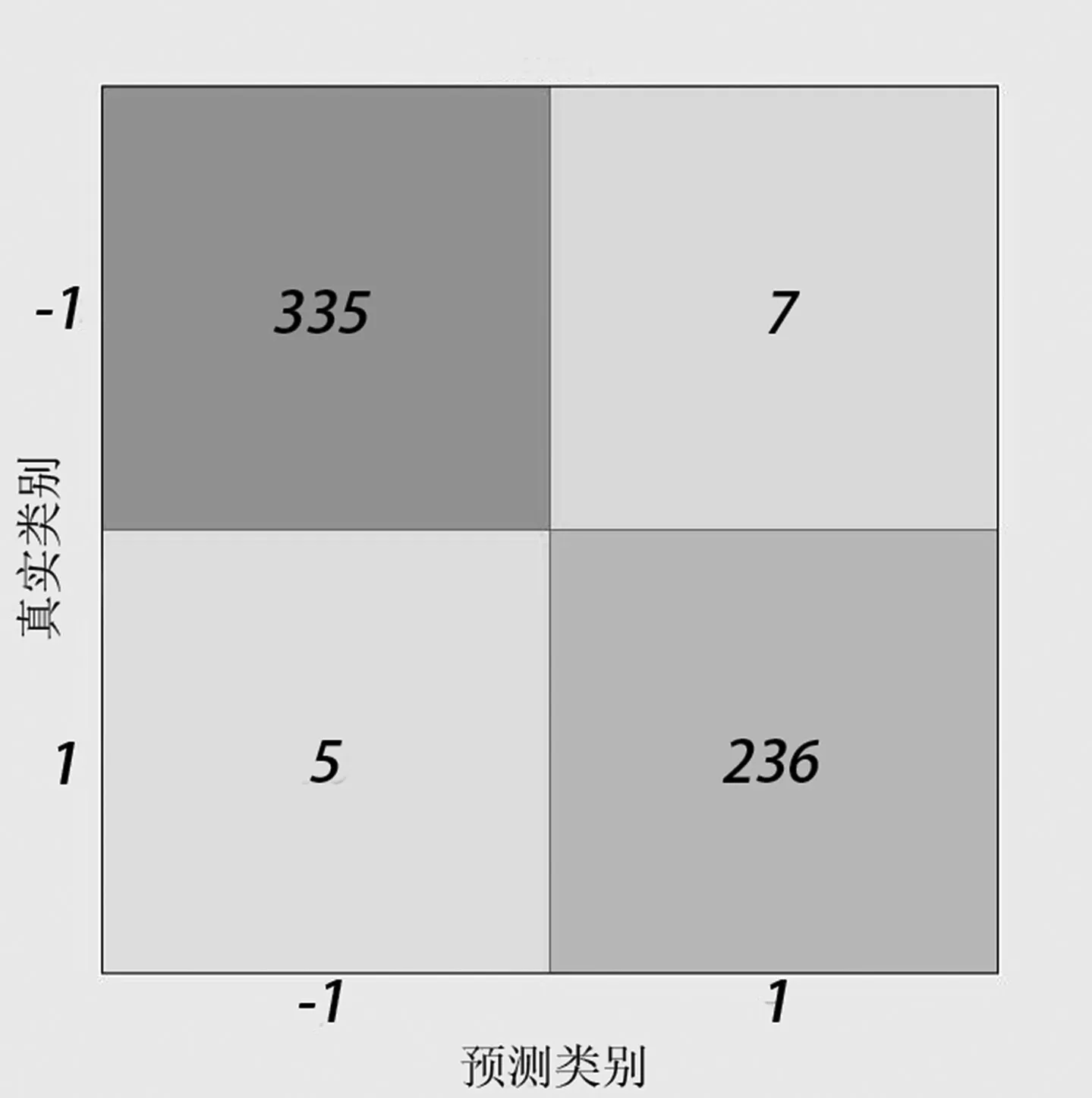
图9 FOREST 混淆矩阵

图10 C-FOREST 算法混淆矩阵

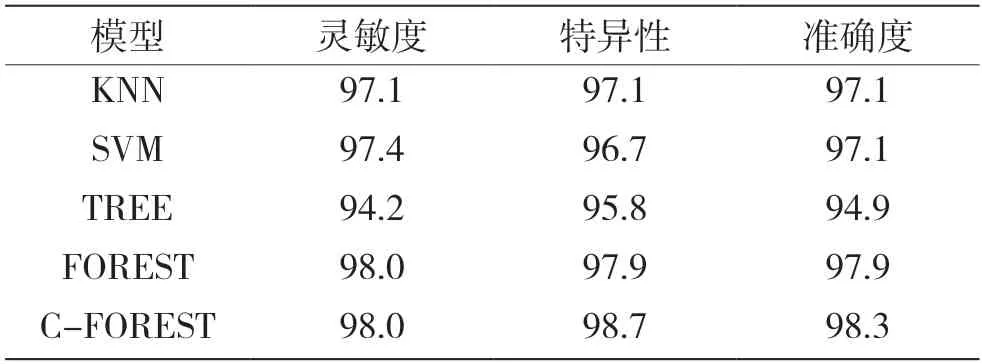
表5 各模型交叉检验的灵敏度、特异性和准确度 %

从表5 可以得出组合随机森林模型较其他分类器模型的灵敏度最大提高了3.8%，特异性最大提高了2.9%，准确度最大提高了3.4%。论文提出的深度组合随机森林算法的分类识别效果好。

为进一步验证本文提出算法的可靠性，将训练好的全部分类器对100 个验证病例样本进行预测。该病例样本的组成如图11 所示，各分类器对新样本预测结果的评价指标如表6 所示。

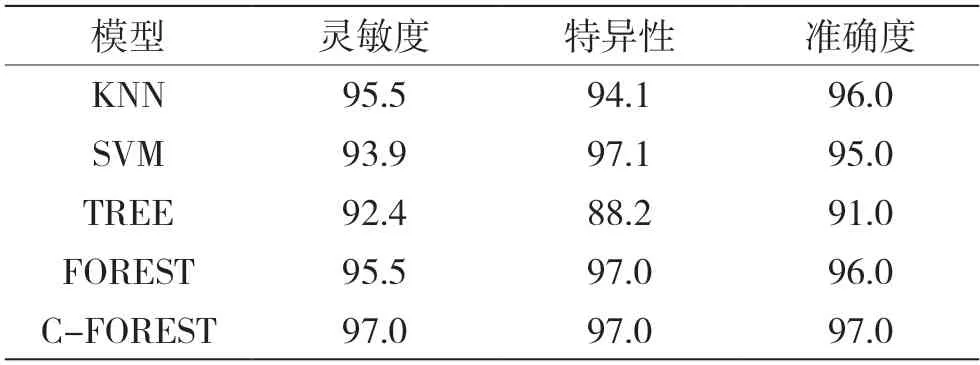
表6 各模型测试的灵敏度、特异性和准确度 %

图11 新病例样本的占比

从表6 可以得出组合随机森林模型对新病例样本的预测准确度较其他分类器模型更高，同时具有最优的灵敏度和特异性。

为了进一步验证本文算法的鲁棒性，将该算法应用于无线定位数据集（Wireless Localization Data Set）和汽车评估数据集（Car Evaluation Data Set）中，实验过程同乳腺癌数据集一致。将模型在训练数据集中进行训练后在验证样本中进行验证，得出的结果如表7、表8 所示。由于无线定位数据集涉及4个类别，而灵敏度和特异性表示的正类和负类的分类情况，同时准确度依然作为分类器最重要的性能指标，因此在表7 中只展示了准确度。

表7 在无线定位数据集上的验证结果 %

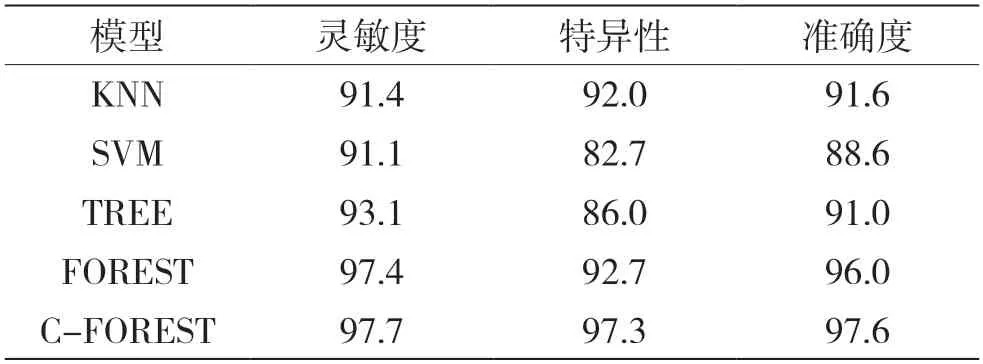
表8 在汽车评估数据集上的验证结果 %

从表7 中可以看出组合模型较其他分类器模型的准确度最大提高了3.7%。从表8 中可以看出组合模型较其他分类器模型的灵敏度最大提高了6.6%，特异性最大提高了14.6%，准确度最大提高了9.0%。论文提出的深度组合随机森林算法的分类识别效果最好，分类准确度达到97.6%。

4 结语

本文针对当前基于单分类器的组合方式不灵活且鲁棒性差的问题，提出了基于深度随机森林的新型组合分类算法。该组合算法结合了随机森林的深度灵活性优点，能够基于不同的数据集找到最优的组合方式，并通过投票方式完成样本类别的预测。在威斯康辛州（诊断）乳腺癌数据集、无线定位数据集和汽车评估数据集上进行验证，实验结果在灵敏度、特异性和准确度这三个方面表明了本文算法不仅有较好的分类效果，还具有较强的鲁棒性。