深层隧道排水系统中井隧水力学特性研究

安瑞冬，游景皓，廖 磊，孟文康，李 嘉

（四川大学 水力学与山区河流开发保护国家重点实验室，四川 成都 610065）

1 研究背景

深层隧道排水系统（深隧），主要由调蓄隧道、入流竖井、通风设施和排泥设施等组成，具有调蓄雨水和排水、控制合流溢流污染的功能［1］。深层隧道排水系统埋深大、可充分利用城市深层地下空间、直接穿越低层建筑、避免大量征地和拆迁［2］，符合现代大城市发展的需求，是防治城市内涝的重要手段之一。最早成功采用深层隧道排水系统的美国芝加哥深层隧道和水库工程，不仅减少了因污水溢流对密歇根湖造成的污染还减少了城市内涝风险［3］。已建或在建的深隧系统已有不少，例如墨西哥东部深层排水隧道工程、马来西亚SMART 深层隧道、巴黎深层调蓄隧道［2］以及伦敦深隧工程［4］等。

深隧系统一般具有超埋深、大流量、高变幅和明满交替运行等特点，因此深隧排水系统就有着高水头、单宽泄流量大、水力振动、竖井掺气以及调蓄隧道排气的技术要求［5-6］。已有研究普遍采用物理模型试验及数值模拟的方法开展研究。设计的泄水竖井主要采用直接跌落式竖井，旋流式竖井、滑道式竖井，折板式竖井及螺旋阶梯竖井。Granata［7］和Camino 等［8］通过直接跌落式竖井的物理模型试验发现，直接跌落式竖井虽然结构简单，过流能力大，但是由于消能作用差，水流直接冲击在竖井底板，造成了较大的冲击破坏，引起了竖井的强烈振动。丁晓唐等［9］与郭新蕾等［10］采用VOF 自由液面捕捉方法和RNGk-ε紊流方程，通过反演不同入流角度下旋流竖井的水力学特性，得出旋流竖井入流角与竖井涡室起旋条件之间的关系。Kennedy 等［11］开展滑道式竖井的物理模型研究并对旋流式竖井进行改进，虽然滑道式竖井的消能效果更好，但在高速水流条件下容易形成水翅等不利流态。Odgaar 等［12］开展关于折板式竖井物理模型试验，通过优化竖井直径、折板空间位置来避免竖井内出现负压，减少进入深层隧道的掺气量，但是该结构对折板强度有较高的力学要求。Qi 等［13］采用VOF 液面捕捉方法对螺旋阶梯式竖井的水力学特性进行了紊流数值模拟，分析了流速及压强分布并发现螺旋阶梯式竖井具有消能率高、流态稳定等优点。

极端降雨期间，入流雨水快速流入调蓄隧道会导致排气受阻并在排气井中产生间歇喷涌现象，对基础设施造成损害［14］，这是深隧系统设计需解决的关键水力学问题。Hamam等［15］指出排水系统中水位快速增加时，截留的气囊会引起排水管道中显著的压力波动。Wright 等［16］通过模型试验研究了间歇喷涌中的水气两相流特性，结合实测数据指出即便静水水头没有超过地面高度也会引起超过地面高度的间歇喷涌［17］。尽管已有观测数据证实了截留气囊会导致压力瞬变，但深隧系统中影响间歇喷涌形成的关键因素及作用机制仍有待确切阐明。

深隧排水系统核心要解决的是泄水竖井抗冲稳定、空化空蚀、水力振动等技术问题。此外，竖井的掺气水流进入隧道后，水流明满交替形成气囊积聚，也可能产生间歇喷涌的破坏。本文采用物理模型试验和两相流数学模型CLSVOF［18-19］，以预期应用于成都市中心城区排水能力提升改造中的深隧系统为例，进行上述关键水力学特性研究，分析不同结构的泄水竖井过流能力、速度分布、压力变化及掺气特性，揭示出调蓄隧道内的水气两相流特性和间歇喷涌关键影响因素。

2 深隧系统结构与模型构建

深层调蓄隧道系统中，竖井和调蓄隧道是其两个重要的组成部分。竖井是从降雨集水到深隧的重要过流部件，承担着入流和排气的双重功能。基于成都市中心城区浅层管网现有设计标准和污水处理厂对初雨处理能力的限制，确定该系统以5年一遇重现期的典型暴雨为设计标准；根据成都近10年的降雨统计，以对应重现期的暴雨量乘以雨型（时程分配）比例，确定了设计暴雨过程；综合考虑城区不同土地类型差异导致的产汇流过程，取上限值30 m3/s作为竖井入流的边界条件。据拟采用盾构设备和施工条件，分别确定了外侧直径为8.5 m 的螺旋阶梯竖井及直径为2.5 m 的旋流式竖井。物理模型试验旨在监测不同位置压力变化并进行结构安全评价，测量过流能力并分析流态，结合预制管径尺寸和供水条件，制作了比尺为1∶14和1∶13的单体竖井模型（两物理模型及测点布设如图1和图2所示）。

图1 螺旋阶梯竖井物理模型及测点分布（单位：m）

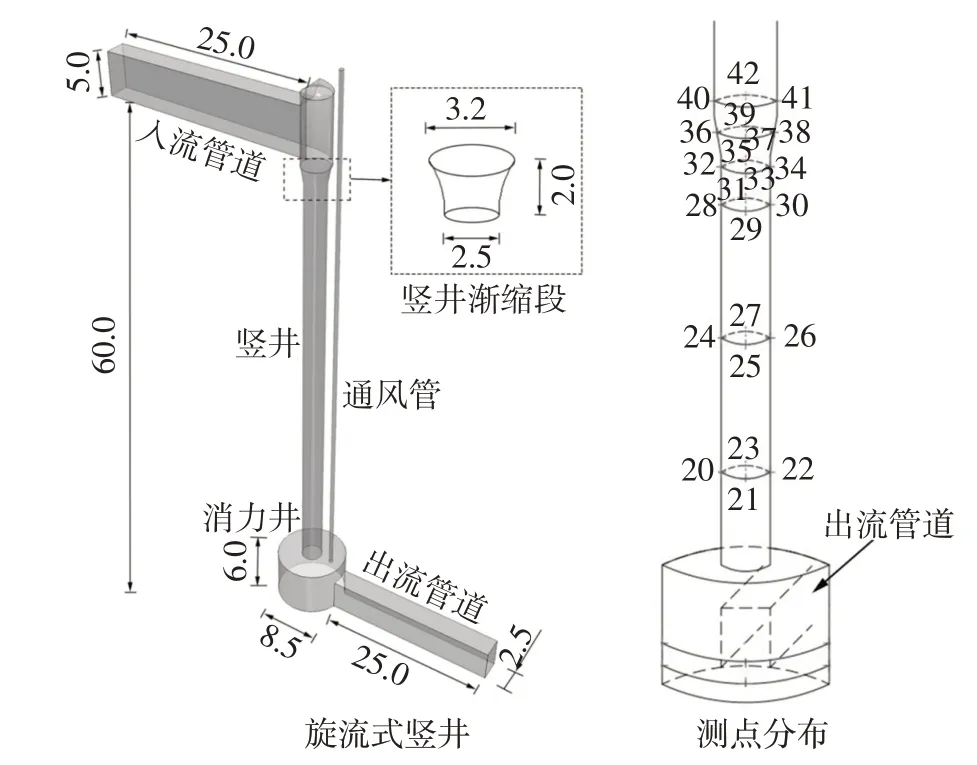
图2 旋流竖井物理模型及测点分布（单位：m）

竖井内掺气水流进入深层调蓄隧道后，明满交替并积聚气囊，当排气受阻时深隧系统就会发生喷涌这种不利情况。针对上述问题，研究也构建了比尺为1∶20的“两井一隧”整体模型（如图3）。深层调蓄隧道采用复合断面，主隧直径为10 m，上层为雨水仓，下层为污水仓。“两井一隧”物理模型的建立旨在监测深层隧道中明满交替时的压力波动。

图3 典型深隧系统井隧整体结构

考虑物理模型的比尺效应，以及明满交替流态中气囊形成和喷涌过程无法有效模拟，研究还根据调蓄隧道的原型尺寸建立了数学模型，更科学地反映其水流规律，如图4所示。

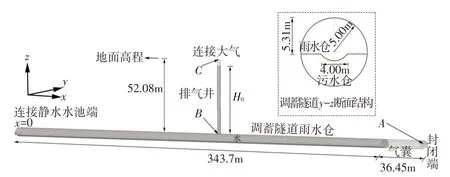
图4 调蓄隧道三维数学模型

3 数学模型及验证

3.1 控制方程为更为精确地捕捉水-气界面，本文采用CLSVOF［18-19］两相流模型，基于Weller［20］所提出的MULES（Multidimensional Universal Limiter with Explicit Solution）-VOF 模型，通过添加LS（level set）函数来实现的。在考虑重力、表面张力的情况下，则CLSVOF模型的控制方程为：

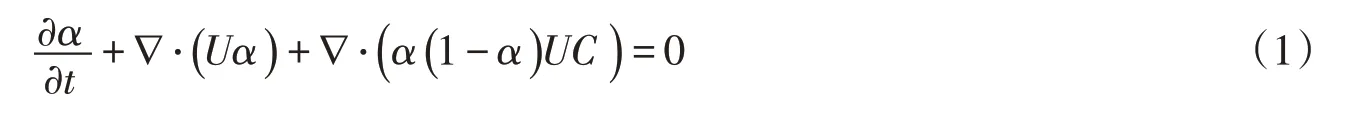
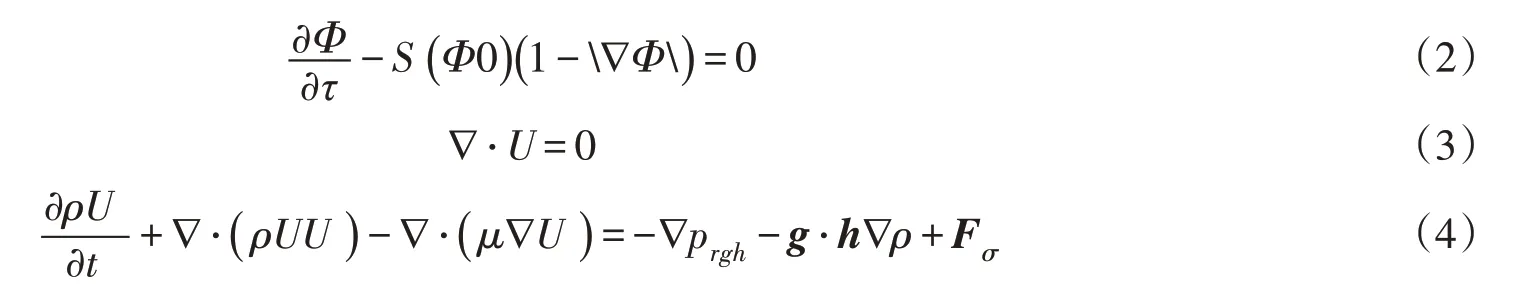
式中：α为网格单元中相体积所占的体积分数；U为流体速度矢量场；∇·(α(1-α)UC)为人工添加的可压缩项，UC为需要模化的速度，其值为保证了界面的压缩；Φ0 为LS函数的初始值Φ0=2(α-0.5)Γ；Γ为一个由网格尺寸决定的参数，取值为其中ΔV为每个网格单元的体积；在获得LS函数初始值之后，LS函数需要通过求解重初始化方程（式（2））来完成重距离化以获得最新的LS 函数［18］；τ为人工时间步长并且取值为对于该方程，当取界面厚度时，即迭代重初始化方程次数为时便可获得接近稳态的数值解。其中S(Φ0 )为阶跃函数［18，21］；ρ为流体密度；U为流体速度矢量场；prgh=p-ρg·h，其中p为压力；g为重力矢量；h为网格单元体心的位置矢量；Fσ为表面张力项且计算公式为其中，σ为表面张力系数，取值为0.0742 N/m；κ(Φ)为由LS函数计算出的自由液面曲率；函数δ(Φ)是用来计算表面张力项的函数［18］。

3.2 计算工况与参数设置模拟分析了相同流量下的旋流式竖井与螺旋阶梯竖井的水力学特性差异，两种竖井计算采用的贴体非结构化网格，进口为速度入口，出口设置为自由出流。而对于深层调蓄隧道中排气竖井直径对间歇喷涌形成机制的影响，研究采用了三种不同管径（r）的排气井，分别为r/R=0.25、r/R=0.5和r/R=1，其中R=5 m为调蓄隧道半径。根据物理模型试验出现的气囊大小及位置，将调蓄隧道的下游端设为封闭端且设置长36.45 m的气囊。调蓄隧道的上游端（x=0 m），设置为压力入口，压力水头为H0=54 m。为观察间歇喷涌喷现象，设置排气井的顶部的圆柱计算区域为大气出口。控制方程中时间项采用欧拉隐式格式，空间项均采用二阶离散格式求解，采用PIMPLE算法［22］求解压力与速度的耦合。

3.3 模型验证模型验证采用与试验相同的数值模拟工况，物理模型试验中在竖井壁面处布设压力测点连续记录。从模拟结果中提取相同位置结果与实测数据进行对比，如图5所示。可以看出两种竖井的实测与计算结果相关性较高，计算压力与实测压力的相对误差最大不超过10%，模拟压力分布结果与试验过程一致。

图5 试验实测与数值模拟压力对比

4 竖井水力学特性

4.1 流态特征两种竖井方案的流态模拟和试验结果如图6和图7所示：

图6 旋流式竖井的流态

图7 螺旋阶梯式竖井的流态

（1）旋流式竖井于进口处起旋，上段主流贴壁螺旋下泄，中下段逐渐脱壁跌落并掺气。消力井和横向出口流道中水流消能，消力井和出口处水气掺混呈不透明状气液混合态。

（2）螺旋阶梯式竖井，水流主要以贴壁旋流的方式旋转跌落到下级阶梯。消能主要在阶梯螺旋跌水过程中实现，其机理是利用阶梯跌水来进行消能。同时由于阶梯侧部通气孔的存在，竖井部分内水流掺气不显著，水气掺混仅出现在竖井底部和出流管道衔接处。垂直阶梯底部存在稳定的空腔。

4.2 流速、压力和消能率分析图8和图9为两种竖井内部的流速分布和压力分布，均以出口底板高程为零基准面。从图8中可以看出旋流竖井内部中水-气界面处的水流速度最大，最大流速为36.1 m/s。而螺旋阶梯式竖井最大流速为15.2 m/s，存在于竖井外壁附近，从横断面（A-A及B-B断面）的速度分布来看空腔附近的速度为5.7 m/s。

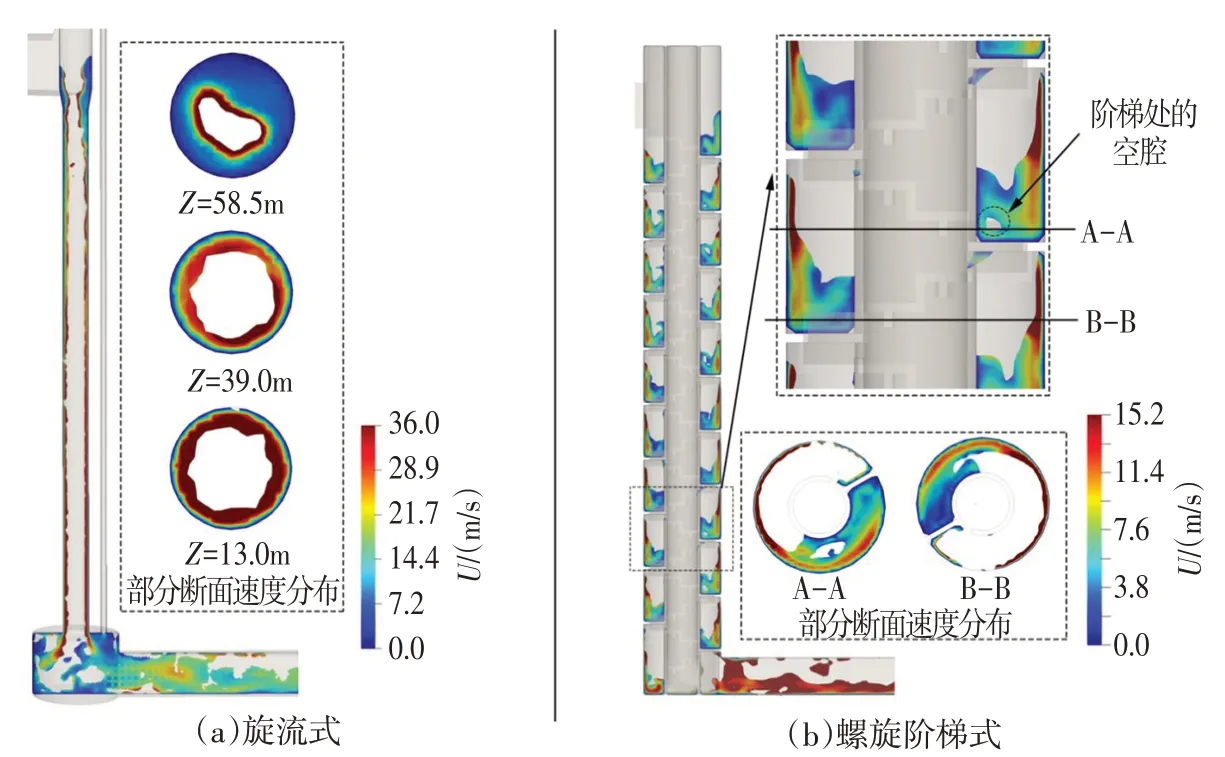
图8 两种竖井方案的速度计算结果

从图9中可以看出，竖井最大压力出现在旋流入口附近的竖井壁面处；在消力井和消力井与出流管道衔接形成了较为明显的负压，最小负压为-19.5 kPa，在高流速下，由于产气量不够可能会引起管道的空蚀破坏。对于螺旋阶梯式竖井，最大压力为35 kPa，出现在竖井外壁处；最小的负压为-7.0 kPa，出现在竖直阶梯底部和小空腔附近。对于两种竖井，消能率、空化数［23］和压力统计如表1所示。旋流竖井最不利处的空化数为0.19，发生空化的可能性高；螺旋阶梯式竖井最不利处的空化数为0.8，发生空化的可能性低。对于两种方案消能率的计算结果由表1所示，可以看出两种竖井方案的消能率均在90%以上，螺旋阶梯式竖井的消能率略大于旋流式竖井的消能率。在水电站设计时竖井与隧道衔接段采用反弧段与压坡的方式，来使得水流流线平顺，减小负压，但在城市排水中压坡段也会增大流速从而对隧道系统造成冲击破坏并带来明满交替等水气两相流问题。

图9 两种竖井方案的压力计算结果

表1 两种竖井方案结果比较

结果表明，两种竖井消能效果显著均在90%以上，其中螺旋阶梯式竖井的消能率略高于旋流式竖井的消能率。两种竖井方案的最大流速分别为36.1 m/s和15.2 m/s，都应该考虑到运行过程中可能对竖井结构产生的冲蚀防护。旋流式竖井最不利处的空化数（0.19）明显低于螺旋阶梯式竖井最不利处的空化数（0.80），高速流动中也应考虑防空蚀措施。

5 调蓄隧道气液两相流分析

5.1 喷涌速度由数值模拟结果可见，在ta=38.4 s 时刻，气囊在调蓄隧道内运动到排气井处。图4中C点为喷涌现象分析的参考点。从图10 中可以看到，管径的变化基本不会影响喷涌之前的水-气运动特性。在ta=38.4 s 之后，不同排气井半径对速度变化响应时刻（为41.4 s）的影响并不明显，速度变化趋势基本一致，但是对速度峰值的影响明显，r/R=0.25、r/R=0.5 和r/R=1 三种情况下发生喷涌期间排气井出口处的速度峰值分别为38.2 m/s、7.1 m/s 和3.6 m/s，速度峰值随管径的变化是非线性的。

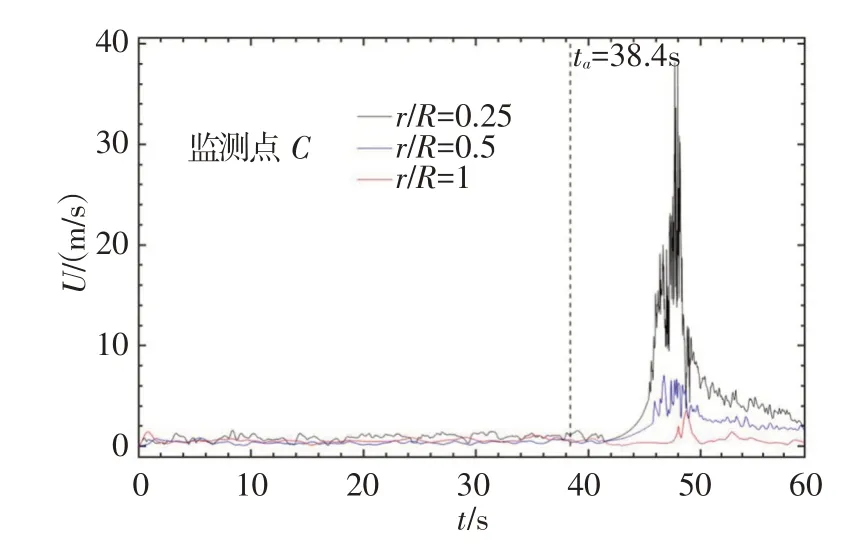
图10 监测点C处的速度变化曲线

5.2 排气井内气液运动特性图11（a）显示了r/R=0.25情况下的气液运动过程，在t=40.2 s和42.4 s时刻，气囊进入排气竖井并在t=44.7 s形成了间歇喷涌，流速达到峰值38.2 m/s；t=46.9 s时排气井中的水柱已经全部喷出，此时调蓄隧道气囊与大气连通；t=49.1 s时，调蓄隧道道内的水气混合后再次进入排气井，在t=51.4 s再次形成间歇喷涌并持续喷涌，此后速度降低且喷涌现象减弱。图11（b）显示了r/R=0.5 情况下的气液运动过程，期间并不会出现调蓄隧道气囊与大气连通现象。根据图11（c），r/R=1情况下并不会出现像前面两种情况下明显的间歇喷涌现象。r/R=0.25、r/R=0.5和r/R=1三种情况下发生喷涌的持续时间分别为49 s、20 s 和11 s； 对于三种情况下发生喷涌最高高度，r/R=0.25、r/R=0.5和r/R=1三种情况分别为71 m、2.1 m和0.3 m。

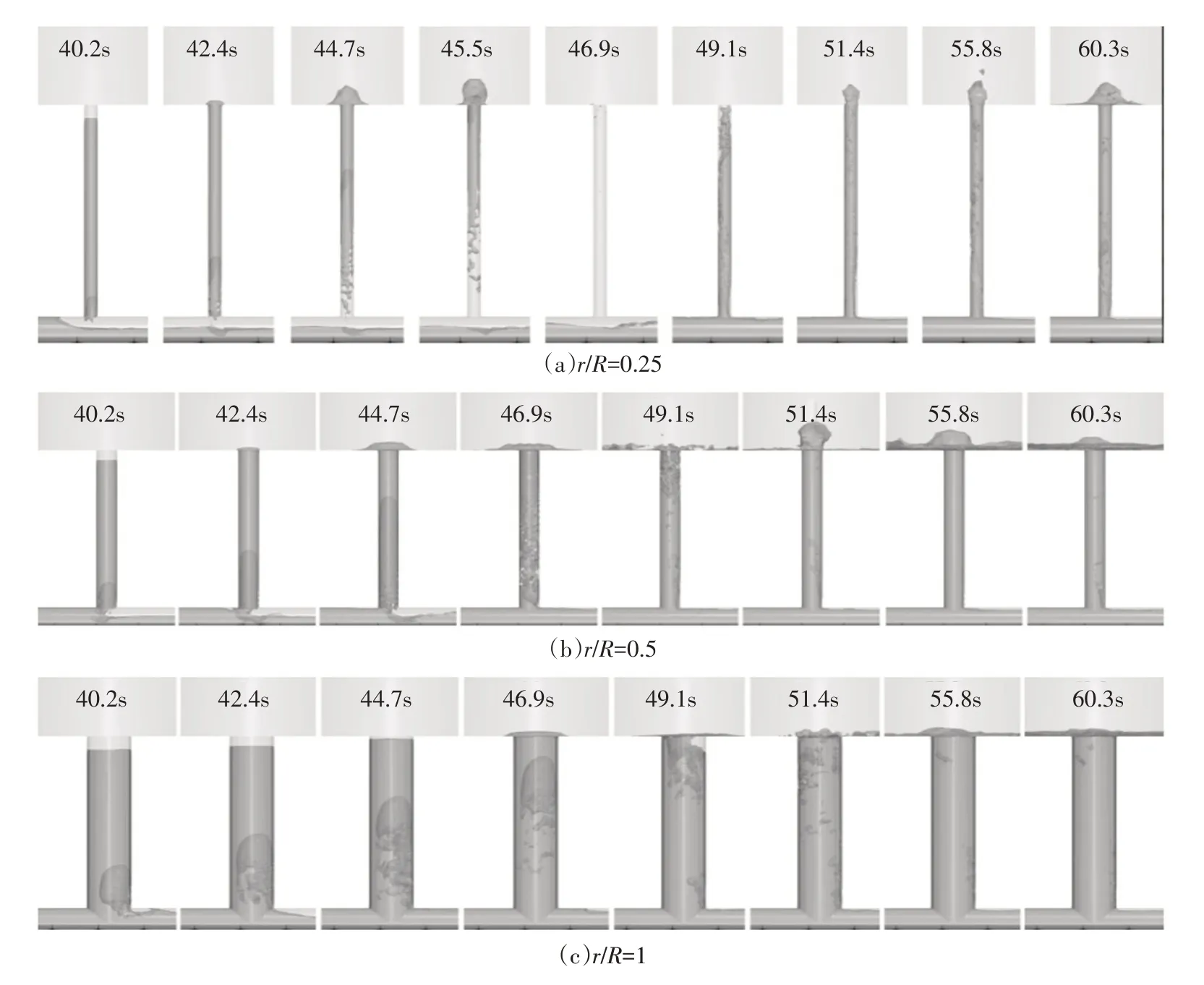
图11 排气井中的气囊运动

5.3 压力波动分析图4所示A、B点的压力变化如图12所示，并进行无量纲化变换，表征A点和B点波动压力H与初始状态时测压管水头f0的相关关系。从图12中可以看出，ta=38.4 s之前A和B的压力波动趋势基本一致。在ta=38.4 s之后，对于r/R=0.25的情况，由于在47.0 s时刻调蓄隧道与大气连通，压力接近0，随后压力陡增并在48.2 s左右达到峰值，为5.35倍的初始测压管水头，在51.4 s左右又降低至测压管水头值。对于r/R=0.5的情况，压力在45.8 s左右降到了0.5 倍的初始状态时的测压管水头，恢复后基本稳定。对于r/R=1的情况，整个过程中的波动压力均维持在与初始状态时的测压管水头相等，并不会发生较为明显的波动。结果表明，间歇喷涌的速度和高度随着管径比r/R缩小而增大，且间歇喷涌的速度及高度与管径比r/R是非线性关系。

图12 监测点A处和监测点B处的压力脉动曲线（改为r/R）

表2 排气井管径对间歇喷涌的影响

6 结论

深层调蓄隧道系统中，竖井和调蓄隧道是其两个重要的组成部分，水力学特性的研究事关工程运行安全。研究基于典型降雨和浅层管网的排水能力，初步确定入流竖井30 m3/s的设计流量，根据拟采用盾构设备和施工条件，分别确定了直径为2.5 m的旋流式竖井及外侧直径为8.5 m的螺旋阶梯竖井两种结构。通过开展竖井水力特性的物理模型试验和数值模拟研究，发现两种不同结构竖井都能满足设计过流要求，消能率都超过90%。但从流态看，旋流竖井中下段主流脱壁并集中在消力井消能，而螺旋阶梯竖井消能主要完成在阶梯跌水过程中且流态更稳定。从竖井排气及空化空蚀风险来看，旋流竖井最大流速达到36.1 m/s，排气受阻，而且消力井内会存在负压区，其附近的空化数为0.19，空化空蚀风险较高。而螺旋阶梯竖井的最大流速为15.2 m/s，排气效果较优，尽管垂直阶梯底角处会存在空腔负压区，但最小空化数为0.80，空化空蚀风险较低。综合来看，不考虑竖井直径条件下，螺旋阶梯式竖井运行风险会明显低于旋流式竖井，水力学特性更利于过流消能和与调蓄隧道的水流衔接。

针对在极端降雨情况下调蓄隧道和排气井中可能发生的间歇喷涌问题，虽然难以控制气囊的产生位置，但采取不同的排气井管径会直接影响间歇喷涌现象的发生，当r/R=0.5和r/R=0.25时会产生较为明显的两次间歇喷涌现象。特别是当r/R=0.25时，两次喷涌间歇出现调蓄隧道短暂与大气连通的现象，这将引起隧道内压力的急剧变化，产生5.35倍的初始状态的测压管水头和38.2 m/s的喷涌速度峰值，这对深层隧道排水系统设施是极为不利的。结果表明，对于本系统而言，适当改变排气井的尺寸可以避免或减小间歇喷涌对排水系统的影响。