三峡水库运行后宜昌-城陵矶河段冲刷重心下移与时空演变

王华琳，郑 珊，谈广鸣，李凌云

（1. 武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉 430072；2. 长江科学院 河流研究所，湖北 武汉 430012）

1 研究背景

大坝修建与大型水库运用会对下游河道的冲淤演变产生重要影响，如我国的三峡水库［1-4］、丹江口水库［5］、小浪底水库［6-7］、三门峡水库［8-10］，国外的Parker 水库［11］、Wloclawek 水库［12］等。坝下河道演变的响应表现在多个方面，在垂向和纵向上，河床呈现不同程度的冲刷下切［13-14］，河道纵比降减小［13］；在横向上，河道可向宽浅或窄深方向发展［11，15］，如波兰的Wloclawek大坝下游河道发生冲刷，河床粗化后冲刷受到抑制，河岸侵蚀加剧，河道展宽［11］，而美国的特里尼蒂河（Trinity River）坝下游河道因水库削峰、岸坡植被生长导致河宽减小20%～60%［15］。在平面形态上，河道内的洲滩格局及河型也可能改变，例如，国内外研究发现坝下河道冲刷使得洲滩面积和数量减少［16-18］，坝下河道可能由辫状向弯曲型转化［19］。

三峡水库运行后，长江中下游河道普遍发生冲刷，其中宜昌至城陵矶河道（以下简称宜城河道）冲刷最为明显。以往研究显示［20］，宜昌至城陵矶、城陵矶至汉口、汉口至湖口2002—2016年累计冲刷量分别为11 亿、4.6 亿和5.2 亿m3，单位河长冲刷强度分别为18.7 万、12.6 万和12.2 万m3/（km·a），可见宜城河段冲刷强度最大。该河段的演变特征有：冲刷主要集中在中枯水河槽［13，21-22］，深泓普遍下切［23］，床沙粗化且沿程粗化程度趋于减弱［24］，粗颗粒泥沙在监利站附近恢复至建坝前水平，而细颗粒悬沙由于河床补给不足，恢复距离较长［22］，不同河型河段的演变发生较大变化，如弯曲河段多发生崩岸与“撇弯切滩”，断面由单槽向“W”型双槽转化［25］，分汊河段发生支汊冲刷发展等演变现象［26］。

以往研究表明冲刷具有向坝下游传播、发展及强度减弱的变化特点［27-28］。例如，董炳江等［20］对2002—2016年宜昌至湖口河段冲淤研究发现，2012年后城陵矶以下河道河床冲刷明显，认为坝下冲刷已发展至城陵矶以下；许全喜等［27］研究发现三峡坝下游粗沙补给带逐渐由宜昌至枝城河段下移至沙市至监利河段。

本研究关注冲刷强度最大的河段（称为冲刷重心），其位置随时间的变化对坝下河道的稳定与防洪安全十分重要。然而，冲刷重心的位置与坝下冲刷延伸所达到的位置有所不同，冲刷重心的位置可能向下游迁移，也可能在上、下游河道之间摆动，由于上荆江河道冲刷强度较大，已有研究认为冲刷重心或主要冲刷带目前仍位于上荆江［37］。罗方冰等［28］对比宜昌至陈家湾（坝下130 km长河段）不同子河段在2002—2014年冲淤量随时间的变化，认为三峡坝下游主冲刷带的发展速率约8 km/a，然而，其研究河段较短，对主冲刷带位置的界定较为模糊，亟需引入定量方法，研究三峡坝下游河道冲刷重心的迁移规律。

由于坝下不同河段的水沙及边界条件不同，河道时空冲淤变化十分复杂，缺乏坝下游冲刷重心变化规律的量化研究。本文以宜城河道为研究对象，基于2002—2018年的水沙与断面实测资料，在分析河道形态变化的基础上，构建河道冲淤变化速率等级的时空矩阵，引入机器学习中kmeans++聚类方法［29］，研究坝下游河道冲淤演变及冲刷重心的迁移规律，为坝下游河道演变的趋势预测与科学管理提供参考。

2 研究区域

如图1 所示，宜城河段位于长江中游，由长约60 km 的宜昌至枝城河段（简称宜枝河段）和长约340 km的荆江河段组成，其中荆江又常分为上荆江（枝城-藕池口）和下荆江（藕池口-城陵矶）。以上荆江杨家垴为界，宜昌至杨家垴为砂卵石河床河段，杨家垴至城陵矶为沙质河床河段［13］。宜枝河段右岸有清江入汇，荆江河段右岸有松滋口、太平口、藕池口和调弦口（已建闸控制）分流向洞庭湖，左岸有沮漳河入汇，洞庭湖出流在城陵矶附近汇入长江。

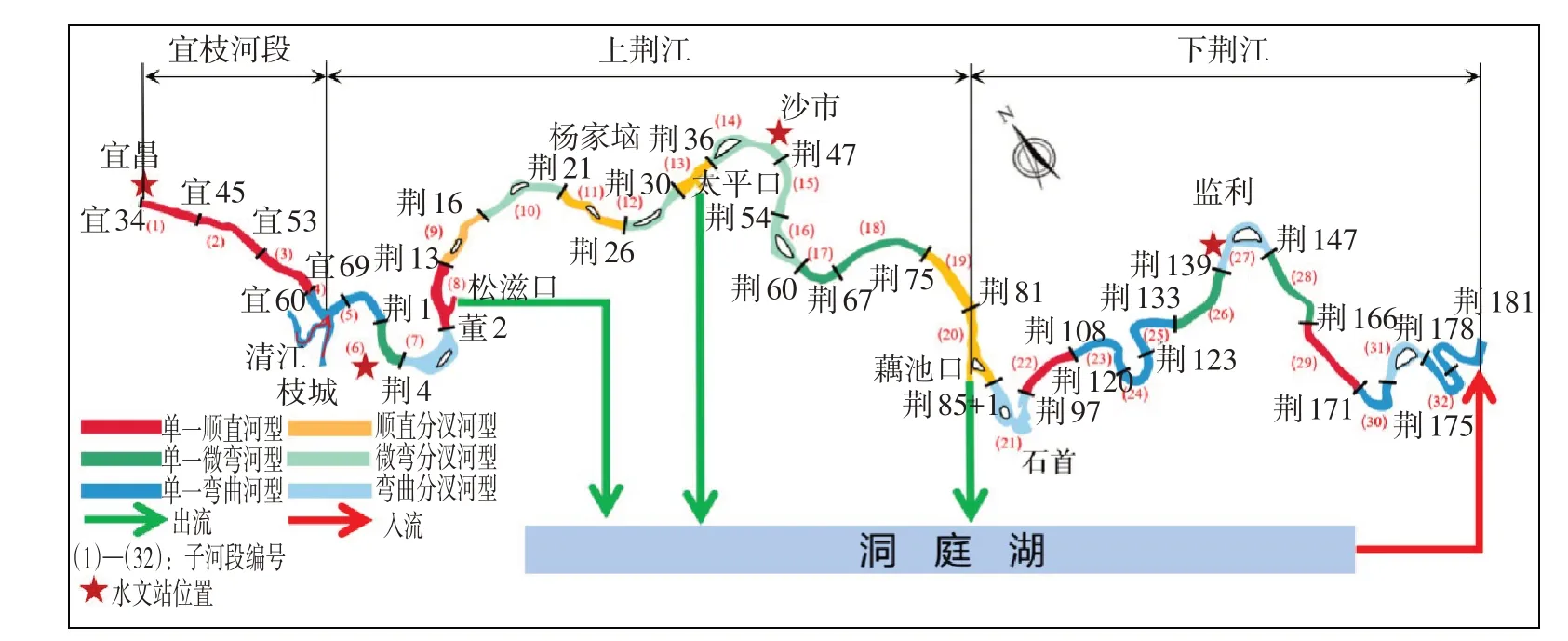
图1 研究区域

三峡水库运用后宜昌、沙市和监利三站（图1）的年均径流量减少约4%～6%，年均来沙量分别比建库前（1991—2002年）减少91%、85%和79%（图2），来沙量减幅沿程减弱，反映了河床冲刷沿程补给泥沙的作用。此外，宜昌站床沙有所粗化，而监利站床沙在建库后波动变化，趋势尚不明显（图3）。

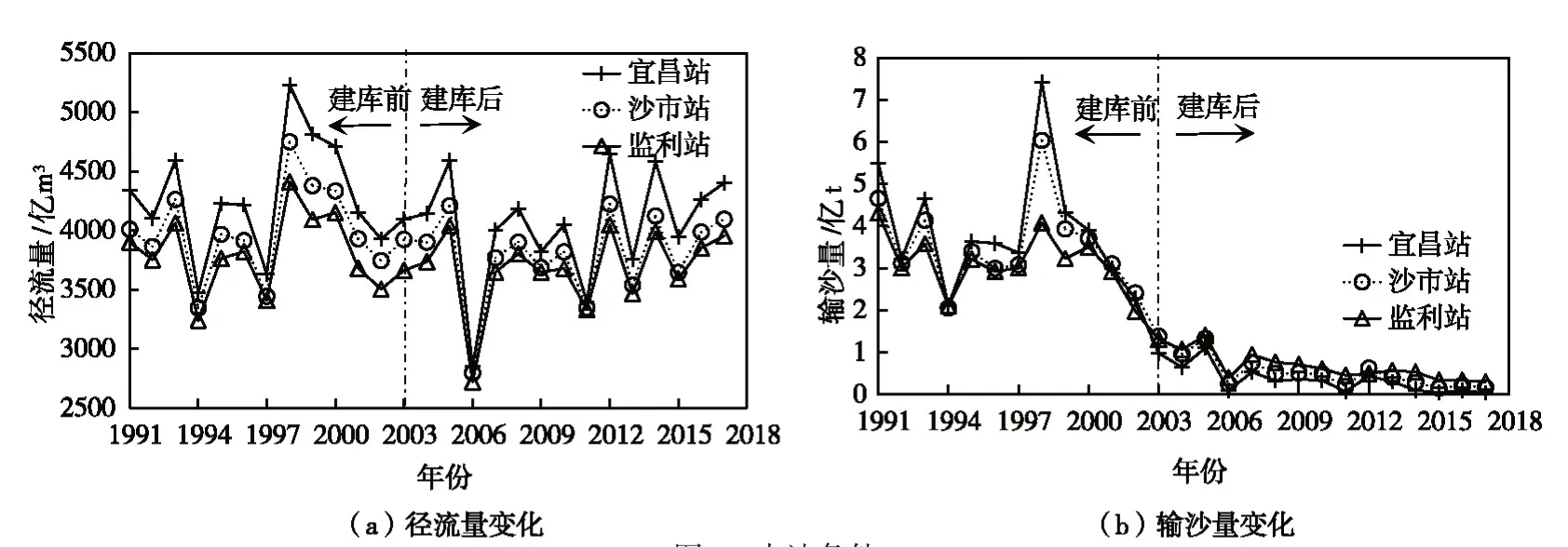
图2 水沙条件

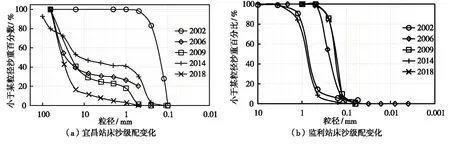
图3 床沙级配变化（资料来自文献［27，31，36］）

综合考虑三峡水库的不同运用方式和三峡上游梯级水库投入运用的时间，将研究时段分为3段［31］：Ⅰ）2003—2007年，三峡水库蓄水初期；Ⅱ）2008—2012年，三峡水库175 m 蓄水期；Ⅲ）2013—2018年，三峡上游梯级水库运用后。3个时段宜昌站对应的年均径流量分别为3936亿、4020亿和4191 亿m3，与时段Ⅰ相比，时段Ⅱ和Ⅲ的年均径流量分别增加2.1%和6.5%；年均来沙量分别为0.67亿、0.30亿和0.11亿t，与时段Ⅰ相比，时段Ⅱ和Ⅲ的年均来沙量分别减少55.2%和83.6%。

空间上，将研究河段划分为32个子河段（图1）。根据河道平面特征和162个观测资料较全的断面（宜34 至荆181 断面）的分布划分子河段，考虑河段为单一或分汊河型，或为顺直、微弯或弯曲河型，可分为6种不同河型（单一顺直、单一微弯、单一弯曲、顺直分汊、微弯分汊和弯曲分汊），分汊型子河段包含完整的江心滩，弯曲型子河段包含弯顶段及部分上、下游衔接段，在考虑河型的同时，尽量避免各子河段的河长差别太大。河道曲率大于1.2为弯曲型，小于1.2为顺直微弯型［30］，为进一步区分顺直与微弯河型，以1.05为界，认为曲率介于1.05 ～1.2为微弯河型，小于1.05为顺直河型，需要说明的是，本文采用1.05为界仅为区分不同子河段的相对弯曲程度，并不一定适用于其它河道。对多汊河段，采用主汊计算河道曲率。划分子河段时不可避免存在主观因素的影响，各子河段冲淤量与划分方法有关，但河道总体的时空冲淤规律不会受到影响。

3 研究方法

3.1 河床形态特征量计算基于实测资料，计算各断面的形态特征量，包括深泓高程、深泓横向摆动速率、平滩水深和平滩面积。平滩面积指平滩高程以下的横断面面积，本文平滩高程根据断面滩唇位置选取［32］，对于无明显滩唇的断面，根据上、下游有滩唇可确定平滩高程的断面资料，拟合平滩高程与河长的关系式，插值得到无明显滩唇的断面处的平滩高程。根据平滩高程确定平滩河宽W和平滩面积A，计算得到平滩水深H。

采用下式计算各断面的年际深泓摆动速率Δx（m/a）：

式中xi和xi+1分别为第i和第i+1年断面深泓点的起点距，m。

根据各断面的河床形态特征量，采用式（2）计算河段平均形态特征量：

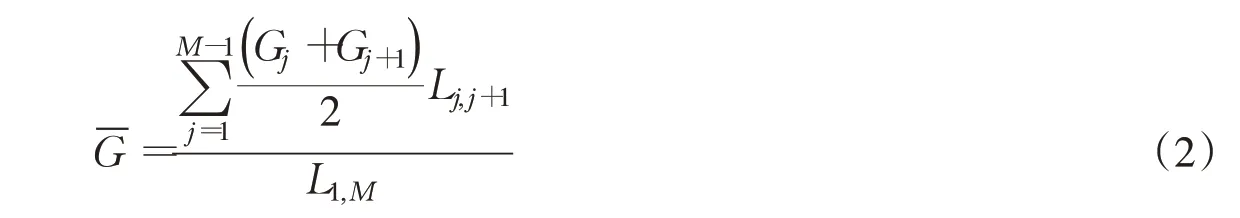
式中：G泛指某一断面的河床演变特征量，为河段尺度的特征量值，可将各断面的深泓高程的变化、深泓横向摆动速率Δx、平滩面积和平滩水深的变化作为G分别代入式（2）计算其河段平均值；Gj和Gj+1分别为第j和第j+1个断面的形态特征量；Lj，j+1为第j与第j+1个断面之间的河长，km；L1，M为河段长度，km；M为河段的断面数。

根据各断面平滩面积，采用式（3）计算河段冲淤量V（m3）：

式中ΔAj和ΔAj+1分别为第j和第j+1个断面平滩面积的变化，m2。

3.2 冲淤等级划分根据2003—2018年32个子河段的平均平滩水深和平滩面积的变化（共512个数据），对平滩面积和平滩水深的变化速率进行分级。除去平滩面积和平滩水深变化最小的前5%的数据（该数据归为0 等级）之后，对剩余数据按出现频率进行等分（各等级出现频率各占23.75%），得到±1、±2、±3和±4四类等级，负数等级代表冲刷，即平滩面积或水深增大，正数代表淤积，即平滩面积或水深减小，各等级对应的平滩面积和平滩水深变化的绝对值范围如图4所示，需要注意的是，由于平滩面积和水深的变化幅度较大，±3和±4等级对应的平滩面积和水深变化的跨度较大，本文按频率划分等级可保证-4等级具有一定的样本点数量，以便于对冲刷强度最大的-4等级对应的样本点进行聚类分析。

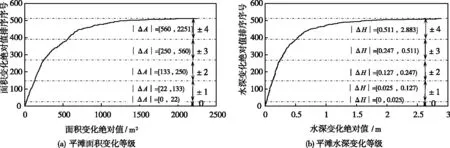
图4 子河段平滩面积和平滩水深变化的等级划分

3.3 冲淤等级的时空聚类根据上述方法得到各子河段每年平滩水深和平滩面积变化的等级，选取冲刷最强烈的-4等级，采用空间聚类中的kmeans++方法［29］，研究冲刷重心（即平滩水深冲刷最强和平滩面积增大最多的子河段区域）随时空的变化规律。

kmeans++方法采用距离作为相似性的评价指标，即两个对象距离越近，相似度越大，由此得到紧凑且独立的簇。对图5所示样本点，以k=2为例说明采用简化kmeans++算法的聚类过程［29］：（a）在N个样本点中随机选择第一个初始中心点A；（b）计算其余N-1点到已有中心点的最短距离D（x），计算各点被选为下一个中心的概率P：

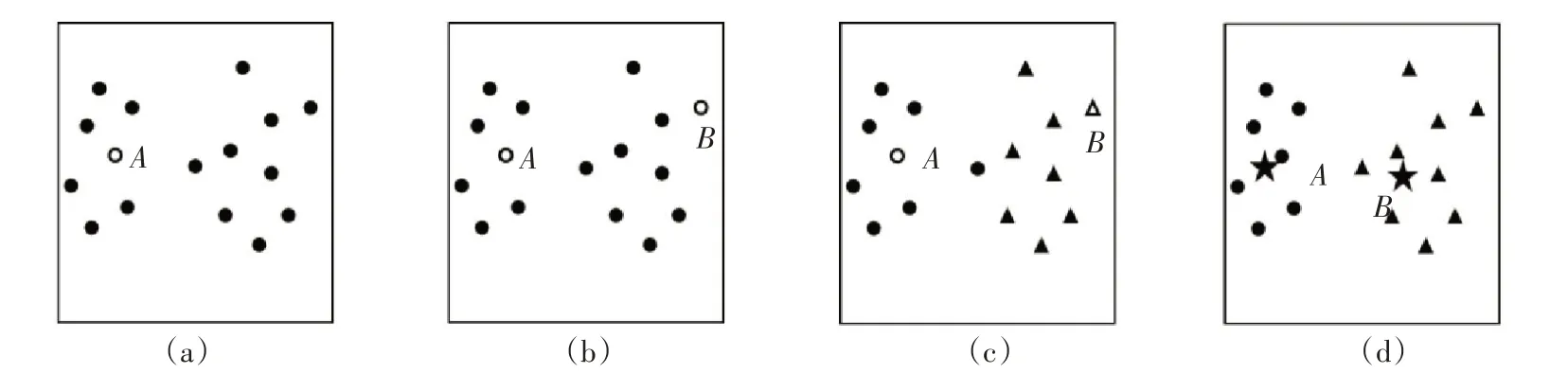
图5 简化kmeans++算法示意

取概率最大的点为第二个中心点，离上一个中心值最远的点B具有最大机会作为下一次选取的中心值；（c）计算各点到两个聚类中心A和B点的距离，按照距离就近原则分类，圆点属于一类，其中心点为A点，三角形点属于另一类，其中心点为B点；（d）按现有分类计算各类重心位置，得到新的聚类重心，重复（c）得到新类簇；迭代至重心位置不再变化。kmeans++方法在步骤（b）时采用轮盘赌算法确定下一个中心点位置［29］，本文对这一方法进行了简化，取概率P最大的点为中心点，这与kmeans++方法的思想核心即离上一个中心值较远的点更有机会作为下一次选取的中心值基本一致。

4 结果分析

4.1 河道冲淤演变

4.1.1 纵向变化 2003—2018年宜城河段河床普遍冲刷下降，河床冲深在空间呈不均衡分布（图6）。平滩水深与深泓高程的变化趋势基本一致（图7），在3个研究时段内，全河段年均深泓调整速率分别为-0.41、-0.17和-0.20 m/a，平滩水深变化速率分别为0.20、0.12和0.14 m/a，冲刷的子河段河长分别占全河段总长的93%、69%和88%，由此可见，蓄水初期（时段Ⅰ）河床冲刷强度最大，175 m蓄水运用后（时段Ⅱ）冲刷减弱，三峡上游梯级水库运用后（时段Ⅲ）冲刷增强，但强度弱于蓄水初期。时段Ⅱ冲刷减弱与河床粗化有关，上游梯级水库运用后冲刷增强与来沙量较时段Ⅱ大大减少有关。

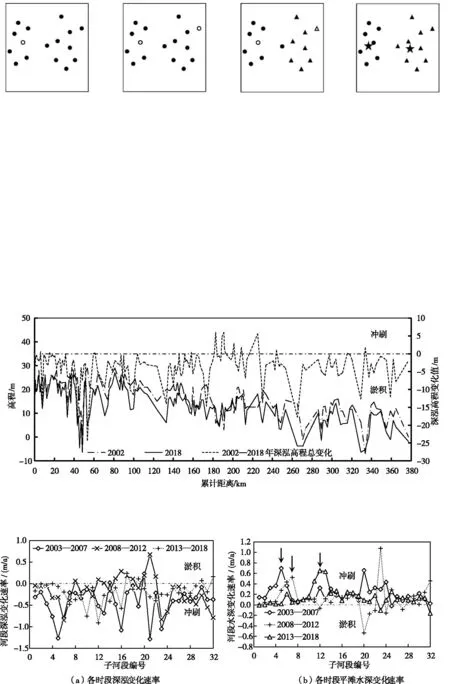
图6 深泓纵剖面及其变化

图7 河床冲淤变化

4.1.2 深泓横向摆动 由于分汊河段包含多个汊道，较难采用统一方法对比单一和分汊型河道深泓的横向摆动速率，因此，本节仅对单一型河段的深泓摆动进行分析。需要注意的是，子河段8（上荆江董2—荆13）受河道心滩影响，以往研究将其归为单一［17］或分汊型［18］河道，本节暂不对这一子河段进行分析。

宜枝河段和下荆江以单一河型为主，宜枝河段受河道边界条件控制横向摆动较弱，下荆江河道深泓摆动强度较大（图8）。除个别子河段外（如子河段18和28），2013—2018年深泓摆动强度明显弱于前期两个时段，说明单一型河道的横向摆动有所减弱。图9 显示了不同典型形态断面的形态变化，位于第4个子河段的宜63断面主槽呈V型，左侧边滩冲刷导致深泓横向摆动，位于第28个子河段的荆149断面趋于W型，主流在心滩两侧频繁摆动，横向摆动速率较大。

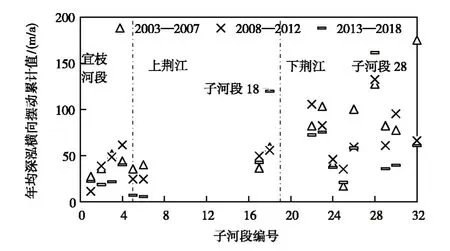
图8 深泓横向摆动速率

图9 深泓摆动的典型断面

4.1.3 河道冲淤 采用式（3）计算得2003—2018年宜城河道累计冲刷量约11.9 亿m3。对比本文方法与其他学者计算不同时段河道冲淤量，考虑所采用的方法有所不同，但相对误差较小（表1），认为本文方法计算的冲刷量结果基本可信。

表1 本文方法与以往研究计算冲淤量结果对比

宜城河道在3个时段内年均冲刷量分别约0.86亿、0.59亿和0.78亿m3，再次证明河道在梯级水库运行后冲刷速率增大，但冲刷强度仍弱于三峡水库运行初期。2003—2018年宜枝、上荆江和下荆江河段单位河长冲刷速率分别为17.4 万、23.6 万和16.8 万m3/（km·a），上荆江的冲刷强度最大，下荆江最小（图10（a））。

3个时段内冲刷强度最大的峰值分别出现在第5、第7和第13子河段（见图10（b）中箭头），即坝下游约85、106和178 km，相应冲刷强度分别为70万、65万和100万m3/（km·a）。冲刷强度最大的峰值随时间不断下移，但第3个时段冲刷峰值最大，可能与梯级水库运用后河道冲刷增强及其它因素（如河道边界条件、采砂等［27］）有关。冲刷强度最大峰值的位置与平滩水深变化最大峰值的位置（如图7（b））一致，说明河道垂向冲深与断面面积增大基本同步，这与以往研究认为宜城河道冲刷总体为垂向冲深、横向展宽居次要地位的结论一致［11，30］。

4.2 冲淤等级时空分布与冲刷重心变化规律

4.2.1 冲淤等级的时空矩阵 2003—2018年32个子河段平滩面积变化速率等级的时空矩阵如图11所示，图中蓝色代表冲刷（平滩面积增大），红褐色代表淤积（平滩面积减小），颜色越深代表冲淤越剧烈。平滩水深变化速率等级与平滩面积变化速率等级的时空分布相似。

计算2003—2018年32 个子河段的平滩面积和平滩水深变化等级的均值和方差，结果如图12 所示，由图可知，除砂卵石河床的宜枝段以外，平滩面积和水沙变化等级的均值和方差具有较显著的向下游增大的趋势，变化等级的均值沿程增大说明越往下游河段冲刷越弱或越易发生淤积，方差沿程增大说明下游河段冲淤等级差异性越大，或越易发生冲淤交替。图11冲淤等级的时空分布矩阵也显示下荆江子河段相对上荆江更易出现冲淤波动。需要说明的是，由于宜枝河段属于山区到平原河流过渡段，河床抗冲性较强，三峡水库运用后冲刷强度不大，甚至在一些年份发生淤积，因此冲淤等级的均值也较大。

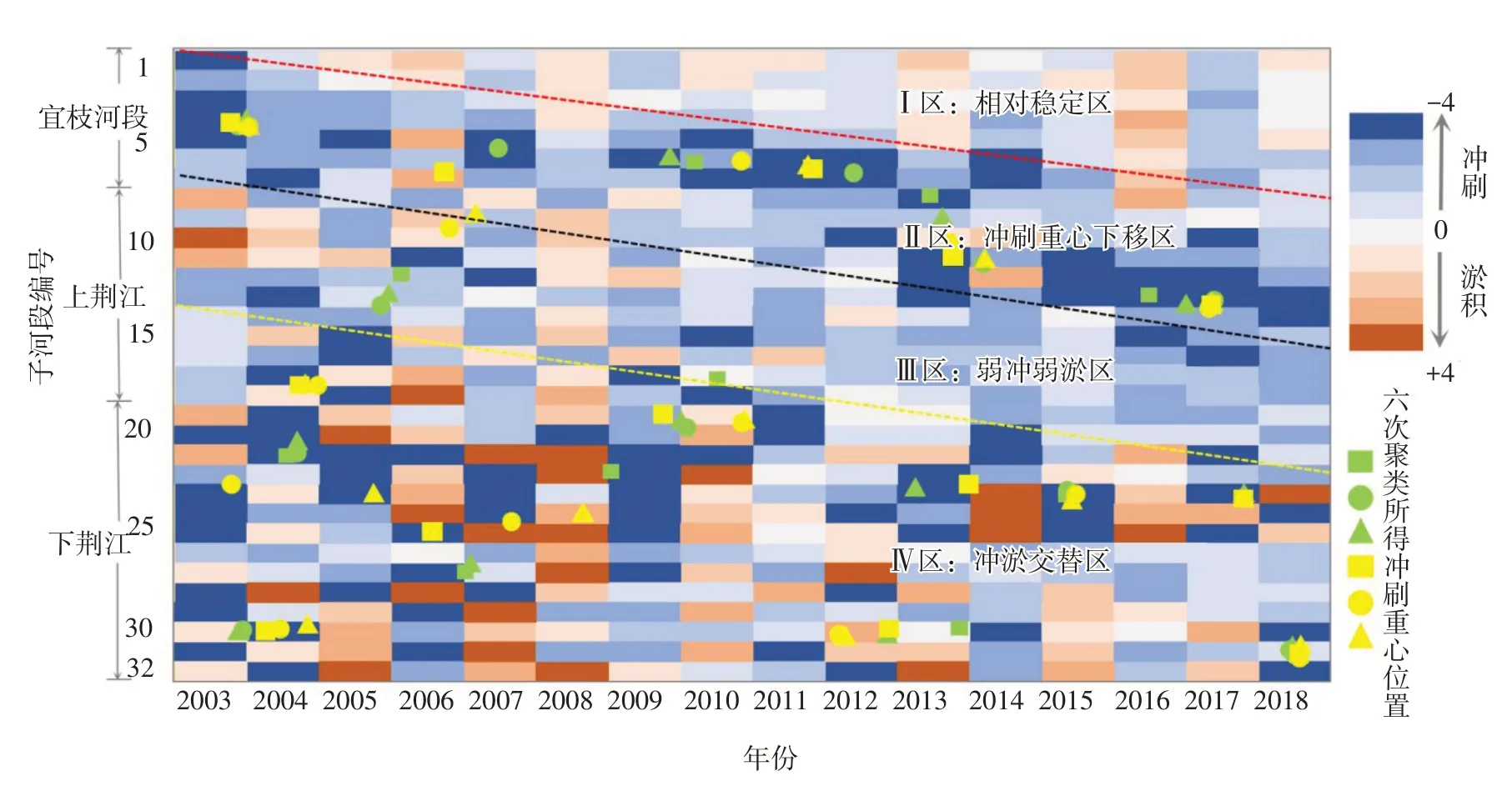
图11 平滩面积变化速率等级的时空分布与冲刷重心

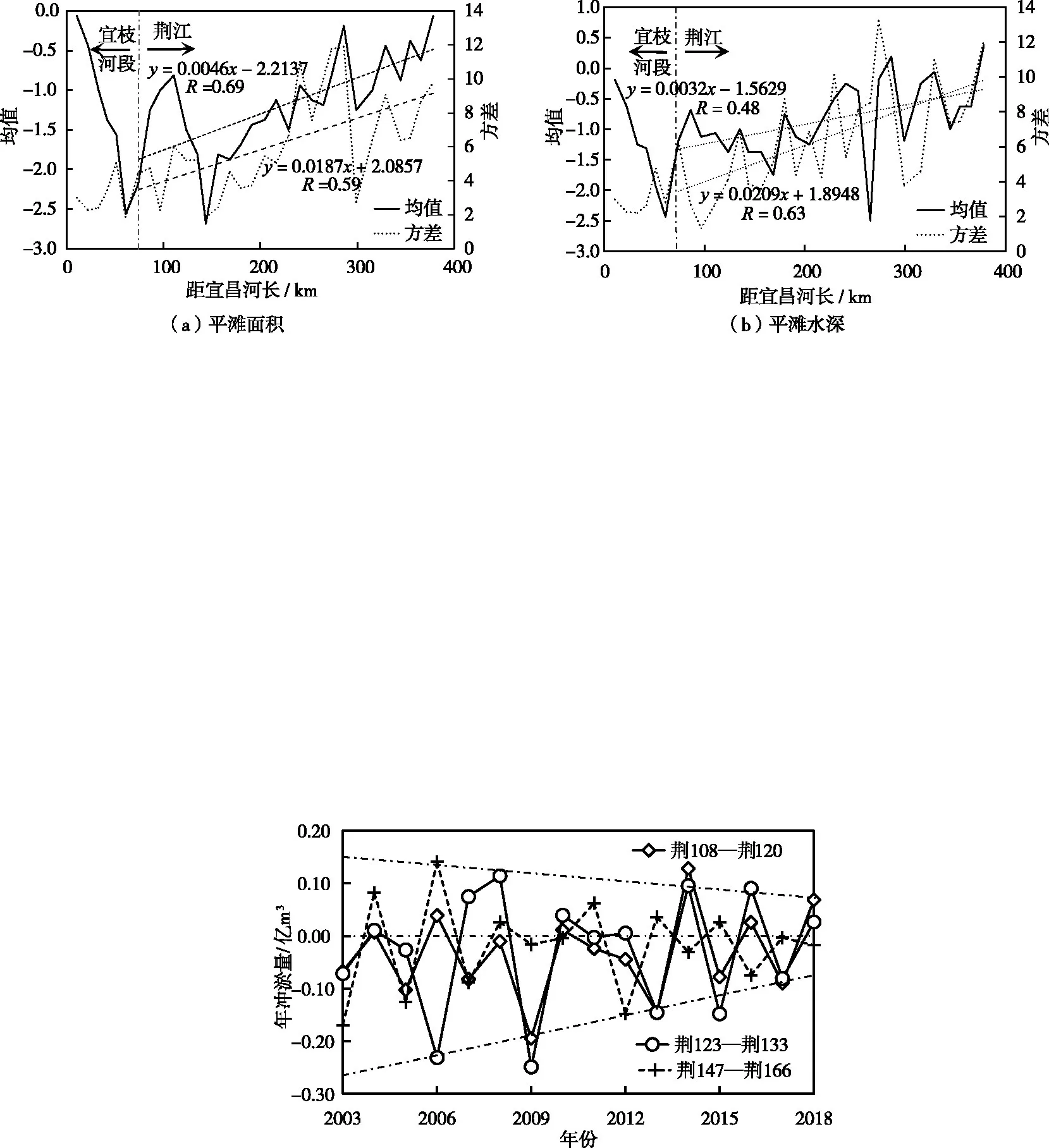
图12 2003—2018年各子河段冲淤等级和方差

4.2.2 冲刷重心的时空分布与迁移 采用kmeans++算法对图11中冲刷等级为-4等级（冲刷速率最大）的样本点进行聚类分析。首先需确定聚类中心个数k，k越大，用聚类中心代表总样本时信息量的丢失程度越小，但当k值太大（如等于样本点个数）时，则达不到分类效果，因此，需针对不同样本点个数选择合适大小的k值。本文对平滩面积变化的-4等级样本点，计算k由1逐渐增大至样本点个数对应的畸变函数（即式（4）右侧分母部分），随着k增大，畸变函数值逐渐减小，当k达到13时，畸变函数值趋近平稳，因此本文取k=13。此外，kmeans++算法随机给出初始聚类中心，本文通过6次随机聚类得到78个聚类中心，其位置较邻近，甚至有重叠，说明初始中心值的随机选取对聚类结果的影响不大。需要说明的是，本文采用的空间聚类算法得到的冲刷重心位置，虽然在个别年份这个位置可能发生淤积，但其代表数年和数个子河段在时空平均意义上的冲刷最强区域的中心，应从较长的时空尺度上理解冲刷重心位置的迁移变化。根据平滩面积变化最大的-4 等级的冲刷重心的聚类结果，可以划分如下4个时空冲淤区域（图11）。

Ⅰ区：相对稳定区，红色虚线以上、矩阵右上角的三角形区域，在这一区域内河道冲淤幅度较小，河道相对稳定，并且冲淤幅度较小的河段或坝下相对稳定区的河长随时间不断增加，至2018年坝下游约140 km长河段均处于坝下游相对稳定区。

Ⅱ区：冲刷重心下移区，红色与黑色虚线内的倾斜带状区域，在这一区域内分布着多个冲刷重心聚类点，这些冲刷重心聚类点具有随时间向下游迁移的趋势。图11红色矩形框显示4.1节中3个时段冲刷峰值所在子河段（5、7和13）的位置，与冲刷重心的聚类结果基本吻合。

Ⅲ区：弱冲弱淤区，黑色虚线与黄色虚线内的倾斜带状区域，这一区域内河道冲淤幅度相对较小，约2010年前河床以弱淤为主，之后以弱冲为主，但冲刷强度明显弱于冲刷重心下移区。

Ⅳ区：冲淤交替区，冲刷和淤积交替出现的概率较大，冲刷重心上、下游波动明显。该区域主要集中于下荆江河段（第20—28子河段），如图13所示，典型子河段（荆108—荆120、荆123—荆133和荆147—荆166）冲淤交替频繁，但冲淤幅度随时间不断降低（图13）。需要说明的是，与其它3个区相同，Ⅳ区内河道冲刷仍占主导，河道整体表现为冲刷，4个区域并没有严格的界限，图11所示分界线仅为示意。平滩水深变化最大的-4等级的聚类结果与平滩面积的聚类结果基本一致。

图13 冲淤交替区代表子河段年冲淤量变化

选取平滩面积和平滩水深聚类所得Ⅱ区中的冲刷重心，得到冲刷重心随时空的分布，如图14所示。蓄水初期冲刷重心下移速率较快，2008年后逐渐减慢，上游梯级水库运用后，冲刷重心下移速率明显加快，至2014年后又有所减慢。采用直线拟合冲刷重心在2003—2018年的迁移变化（对平滩面积R=0.92，对平滩水深R=0.96），拟合线的斜率可作为三峡水库运用以来冲刷重心的平均下移速率，约为7.5 km/a。

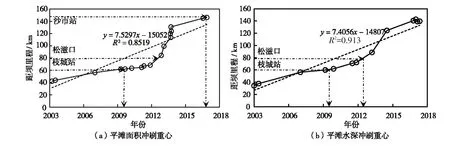
图14 冲刷重心随时间下移

上述冲刷重心的迁移特点与以往研究结论基本一致。例如，本文得到2003—2018年冲刷重心的平均下移速率约为7.5 km/a，与罗方冰等［28］得到三峡坝下游主冲刷带的发展速率约8 km/a 基本一致，但本文冲刷重心下移速率是基于量化的数据处理与分析得到的，并且显示了不同时段冲刷重心下移的快慢变化。本文结果显示冲刷重心在2010年左右下移至宜枝河段末端（图11 与图14），以往研究显示三峡水库运用后至2010年左右宜枝河段床沙粗化明显、之后变化不大，河道冲刷减弱［14，34］，这一变化规律与冲刷重心下移至宜枝河段以下有关。此外，图11 和图14 显示2013年冲刷中心下移至宜昌下游约100 km 的位置，相对稳定区基本涵盖松滋口及其上游河段范围，这与岳红艳等［35］的研究结论即松滋口以上河段在2013年以后冲刷速率明显减缓、河道平面形态及河势基本稳定一致。

图15分别给出了4个分区对应的典型子河段累计冲刷量的变化过程。子河段1（宜34—宜45）位于相对稳定区（Ⅰ区），累计冲刷量随时间变化不大；子河段4（宜60—宜69）于2010年左右由冲刷重心下移区（Ⅱ区）进入相对稳定区（Ⅰ区），冲刷速率由快变慢；子河段13（荆30—荆36）于2012年左右由弱冲弱淤区（Ⅲ区）进入冲刷重心下移区（Ⅱ区），冲刷速率由慢变快；子河段28（荆147—荆166）位于冲淤交替区（Ⅳ区），河道以冲为主，但累计冲刷量波动较明显。

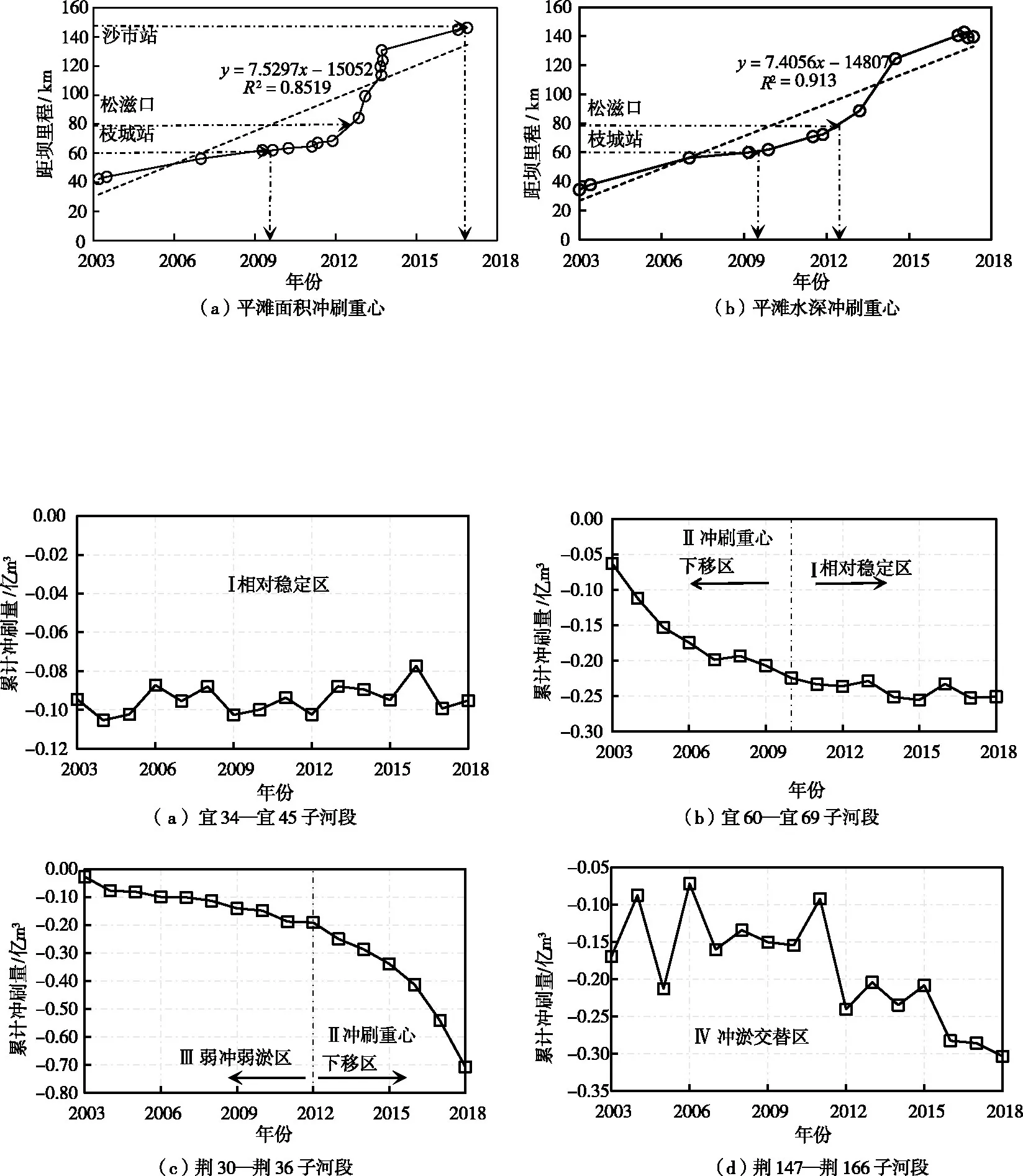
图15 4个区典型子河段的累计冲刷量变化

5 结论

三峡水库运用后，宜昌至城陵矶河道经历了蓄水初期冲刷较强（2003—2007）——正常蓄水后冲刷减弱（2008—2012）——上游梯级水库运用后冲刷增强（2013—2018）三个阶段；在3 个时段内，平滩水深变化速率分别为0.20、0.12 和0.14 m/a，年均冲刷量分别约0.86 亿、0.59 亿和0.78 亿m3。单一河型河段在2013年后横向摆动有所减弱。建立了2003—2018年32 个子河段平滩面积和平滩水深冲淤变化等级的时空分布矩阵，发现冲淤等级的均值和方差沿程增大，表明往下游河道冲刷逐渐减弱、年际冲淤交替越频繁。以顺直微弯分汊型为主的上荆江河道普遍冲刷，而以弯曲和弯曲分汊为主的下荆江河道冲淤交替频繁。针对平滩面积和平滩水深增速最大等级对应的子河段进行聚类分析，发现冲刷重心具有向下游迁移的变化特点，在三峡蓄水初期冲刷重心向下迁移较快，之后减缓，在上游梯级水库运用后，冲刷重心下移速率明显加快，之后再次减缓，2003—2018年冲刷重心平均下移速率约7.5 km/a；至2018年冲刷重心已下移至坝下游约140 km处。未来冲刷重心可能继续沿坝下游河道迁移和发展，然而，其变化受到与来水沙条件和河道边界调整的影响，具有较强的不确定性，考虑三峡水库运行时间较短，后续需在更长时空尺度上深入研究冲刷重心的时空迁移规律与影响机理。