基于透明土技术与颗粒流方法联合开展管涌细观机理研究

倪小东，寇恒绮，左翔宇，王 媛，陆江发

（河海大学 岩土力学与堤坝工程教育部重点实验室，江苏 南京 210098）

1 研究背景

管涌是大坝、围堰等与地下水有关的构筑物发生破坏的主要因素之一，因其发生频率高、危害性大，一直以来是渗流研究领域的重中之重［1-3］。基于细观尺度，管涌形成与发展是土体内部力链结构网络破坏与重构的过程。

管涌作为渗流灾害的重点防治对象，研究人员对其发生、发展细观机理进行了大量研究。模型试验方面：CHEN［4］、RICHARDS［5-6］相继开展常规三轴压缩试验和真三轴试验，发现土体临界摩擦角随细颗粒流失而降低、土体的应力-应变状态也随之从剪胀转变为压缩；周健、姚志雄等［7-9］利用显微摄像可视化跟踪技术等量测手段，开展砂土管涌机理与管涌型土滤层防治的试验研究，从细观尺度揭示颗粒级配、不同层间系数对管涌发生、发展机理的影响。但上述模型试验获得的数据往往是模型边界面的少量离散点信息（颗粒流失量、临界水力梯度、孔口流量），无法对土体内部颗粒运移进行全方位、实时的监测。数值模拟方面：土具有碎散性，有限元中渗流与变形耦合分析能够考虑土颗粒与流体之间的相互作用，但该方法基于连续介质理论，而离散元则是基于非连续介质理论的方法，在模拟破碎松散物质方面具备优势。于是，倪小东等［10］通过PFC数值模拟与管涌砂槽试验对比分析，得出PFC数值模拟结果与室内实验结果较为接近，表明应用颗粒流法开展管涌细观机理研究的可行性；陈闻潇等［11］基于长江大堤管涌案例，采用PFC-CFD 方法开展堤坝管涌渗透流体变化规律的数值模拟研究；李晓庆等［12］基于离散元理论和流固耦合效应，利用PFC3D程序建立基土-滤层渗流模型，研究不同层间系数对管涌发生发展的影响。

随着透明土技术的出现与发展［13-15］，众多学者将该技术应用于土体渗流领域的研究中：孔纲强等［16］进行了不同种类透明土的电渗模型试验，探讨孔隙流体对透明土内部渗流场的影响规律；SANVITALI［17］采用PLIF 技术开展泥石流研究，成功获取了土体颗粒位移信息；谷敬云等［18］基于PLIF 研制潜蚀可视化试验装置，实现对透明土内部颗粒运移的动态监测。在细观尺度层面，力链结构网络演化对土体变形有重要影响：孙其成等［19］以二维颗粒体系单轴压缩为例，指出强力链网络与体系宏观性质直接相关；王金安等［20］基于光弹原理，通过颗粒体双轴加载试验，揭示颗粒体力链形成、发展过程及力链分布形态；徐华等［21］基于颗粒流模拟，从力链结构网络的角度分析川藏铁路红层改良路基填料的变形特性。粗细颗粒相互作用促进接触力链重新分布，而管涌便是细颗粒在渗流力作用下于粗颗粒间隙中流动的一种现象，因此将力链结构应用于管涌发生、发展细观机理的研究是可行的。

本文基于透明土技术与PLIF自行设计可视化管涌模型试验平台，应用MRI技术与颗粒流PFC3D程序对模型中的透明土进行三维重构，通过相同工况下模型试验与数值模拟的对比分析，验证用该方法开展管涌细观机理研究的可行性。综上论述，颗粒级配、细料含量、颗粒摩擦系数、土样应力状态等因素都会对管涌的发生、发展产生影响，结合不同应力状态对管涌型土的细观影响本就体现在力链及孔隙喉径分布不同，并且由于本文选用的透明土材料（水基高分子水凝胶）偏软，所以暂时没有开展不同应力状态下管涌发生、发展细观机理的试验研究，而是开展了不同颗粒级配、细料含量、颗粒摩擦系数三种工况下的数值模拟试验，并从颗粒间接触力链的角度揭示该机理。

2 可视化管涌模型试验

2.1 试验装置设计本文自行研制的可视化透明土模型试验平台主要包括：透明模型箱、自循环常水头控制装置、PLIF数字采集系统（如图1）。

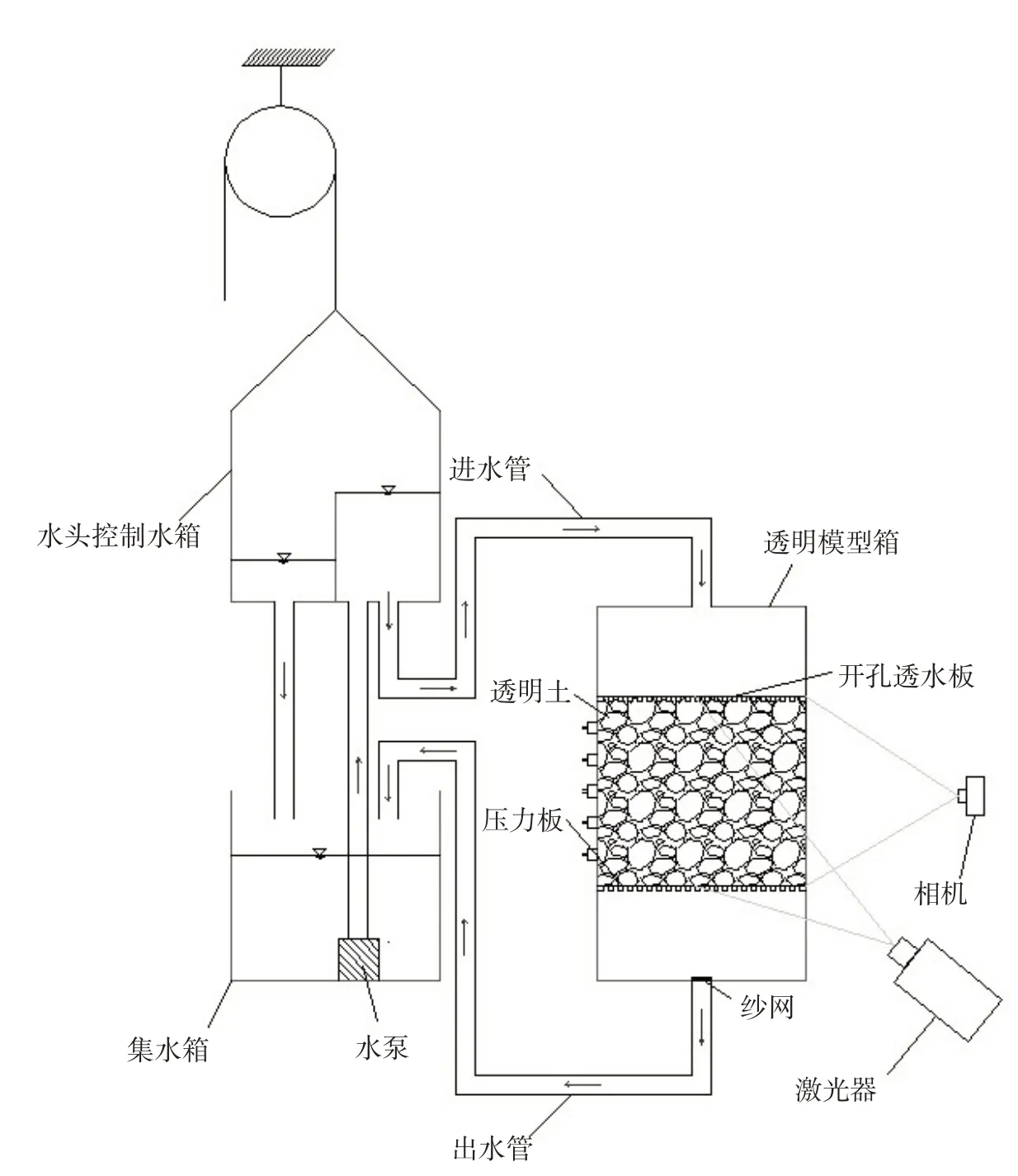
图1 模型试验装置示意

透明模型箱（图2）为150 mm×150 mm×200 mm的有机玻璃长方体，箱内区域设置自上而下分别为缓冲区、填样区以及细颗粒收集区，缓冲区与填样区中间设置一开细孔透水板（重量较小，可忽略），细孔直径为5 mm以保证粗颗粒无法通过细孔，模型箱上下两面各开一孔，侧面透水板以下50 mm、80 mm、110 mm、140 mm处各开一孔，上、下孔分别连接进水管、出水管，侧孔安装孔压计。自循环水头控制装置包括水箱、水箱高度控制装置、储水箱及潜水泵四个部分，其中潜水泵可调节抽水流量，水箱高度控制装置包括直线控制滑块及钢丝绳，水箱通过钢丝绳与滑块连接，通过控制滑块的移动使水箱升至试验所需高度。PLIF 数字采集系统包括CCD 相机及扇面激光发射器两部分（图2），所述扇面激光发射器安放直线滑台上，直线滑台可按预定速度移动，滑台移动方向平行于透明模型箱中的一个侧面，CCD相机拍摄透明土样的散斑视频信息，用于后期三维重构，试验中高速相机轴线垂直于激光源轴线，且两轴线交点位于透明土填样区内。

图2 可视化试验装置

2.2 试验土样制备经查阅相关文献［22-26］，水晶珠（水基高分子水凝胶）适用于模拟较软土渗透变形，而熔融石英砂适用于模拟天然砂土的渗透变形（颗粒形成的孔隙中能够被透过的最大颗粒受颗粒形态影响极大）。因此本文在研究前期也采用了熔融石英砂作为透明土固相材料，并结合上述方法成功实现了对熔融石英砂二维切片的三维重构。考虑从力链角度进行管涌发展过程分析，且目前处于应用MRI技术开展透明土无损非介入式内管涌侵蚀机理研究的初步阶段，本文选用水晶珠作为透明土固体颗粒，孔隙流体则选用无水乙醇和蒸馏水的混合液。

水晶珠具有吸水膨胀性（图3），吸水膨胀前后体积比在1/10 ～1/5范围，进而可根据不同级配制成不同孔隙率的土体。试样制备过程中，将吸水充分的粗细骨料（不同粒径大小的水晶珠）放入孔隙流体中，借助阿贝折射仪量测折射率，采用二分法对无水乙醇和蒸馏水的配比进行调整，直至混合液与水晶珠的折射率基本一致。试样具体参数见表1，颗粒级配曲线如图4所示。根据颗粒流失的稳定级配条件［27-28］，采用H/F法判定土样是否发生管涌，其中F为小于任意细粒直径D的颗粒质量百分数，H为粒径D～4D的颗粒质量百分数。本节土样（H/F）min＜1，因此不满足渗流稳定级配条件，为管涌型土。

图3 水晶珠

表1 试验土样基本参数

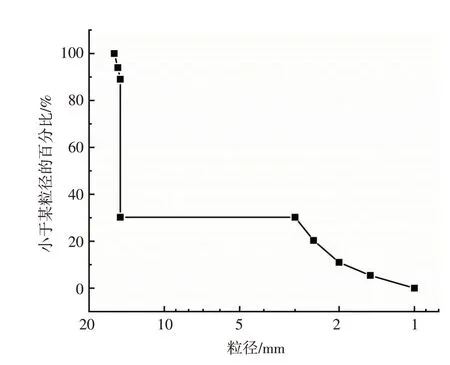
图4 试验土样颗粒级配

2.3 试验步骤试验开始之前：将制备好的透明土装入透明模型箱中，在供水装置内注入配制好的孔隙流体并添加荧光剂，放置开孔透水板将缓冲区与填样区分隔开，调整固定激光器的导轨滑台使其按照规定速度（1 mm/s）移动。试验开始之后：打开进水管阀和出水管阀，使孔隙流体通过透水板进入模型箱内部；打开激光发射器并调整激光切面角度，使其垂直射入饱和透明土样形成散斑场（如图5）；打开CCD相机并调整可视范围，使其包含整个土样，之后对激光器随导轨滑台缓慢匀速移动展开拍摄，提取各截面切片图像以备后期土样三维重构（详见第3节）；拍摄完毕后，打开水泵，控制水箱高度使饱和透明土样在常水头下发生管涌，同时将流量计、孔压计的数据传输至计算机进行数据处理。

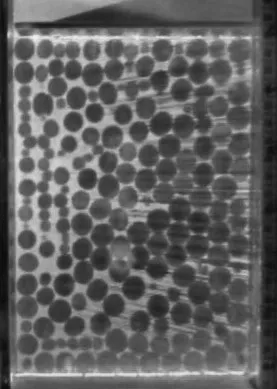
图5 透明土切面散斑效果

2.4 试验结果试验过程中土样发生管涌，土样中细颗粒随流体一起流失，在初始阶段流体中含细颗粒数较多，流量增大较快，模型箱中颗粒发生错动位移，渗流通道不断调整且逐渐扩大。随时间推移，流体中含细颗粒数逐渐减少，流量逐渐保持稳定，模型箱中仅存少量因渗流路径被粗颗粒阻挡而无法流失的细颗粒。模型出砂量、孔口流量和孔压数值随时间的变化规律详见3.3节。

3 数值模拟

3.1 透明土样三维重构借助Matlab 图像工具箱对CCD 相机拍摄视频截取，获得透明土样二维切片集合。基于MRI 原理，应用Avizo 软件对二维切片集合进行有序堆叠（图6）、降噪，对高亮孔隙流体和灰暗颗粒进行二值化分割（图8），使用体绘制命令对处理后的二维切片集合进行三维重构（渲染后如图7（a）所示），通过孔隙像素与总像素比值计算重构模型孔隙率，与实际模型孔隙率相差不大。

图6 二维切片堆叠效果

图7 透明土样三维重构

图8 切片二值化分割

3.2 数值模型建立与参数设置对Avizo 重构模型所提取的颗粒、孔隙信息进行坐标处理并制成PFC3D程序内能够读取的Text文件，通过Loop循环使模拟球颗粒按实际半径生成，在此基础上进行区域设置（缓冲区、填样区、透水板和不透水边界与实际模型保持一致）、网格划分（考虑模型最小流域宽度与网格宽度之比≥5且流体网格最小宽度与颗粒粒径之比≥3的前提下，网格沿坐标轴的个数划分为X=5、Z=5及Y=5。）与颗粒摩擦系数校正，完成PFC3D程序建模（图9）。颗粒间接触模型选用线性接触，不考虑黏性，模型计算参数设置如表2所示，随后开展与第2节相同水头下的颗粒流数值模拟试验。

表2 重构模型计算参数表

图9 数值模型建立

3.3 室内试验与数值模拟对比分析统计第2节室内试验模型和本节相应的重构土样数值模型在距离上游H/3、H/2、2H/3处二维切片的孔隙率数值变化（二维切片孔隙率在0.15 ～0.20范围）、在30 s、50 s、80 s、130 s、430 s、830 s时刻的出砂量、孔口流量和孔压数值，分别绘制于图10、图11和图12中。

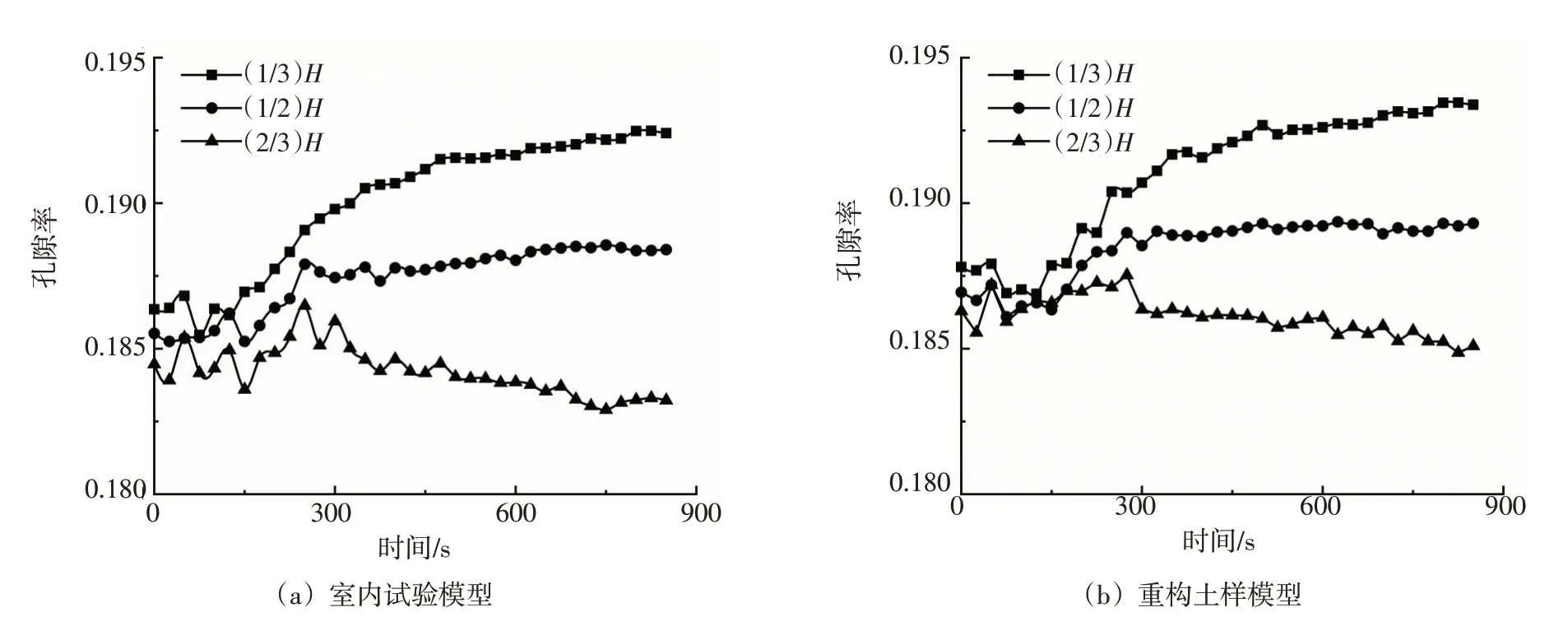
图10 距上游各高度处二维切片孔隙率变化

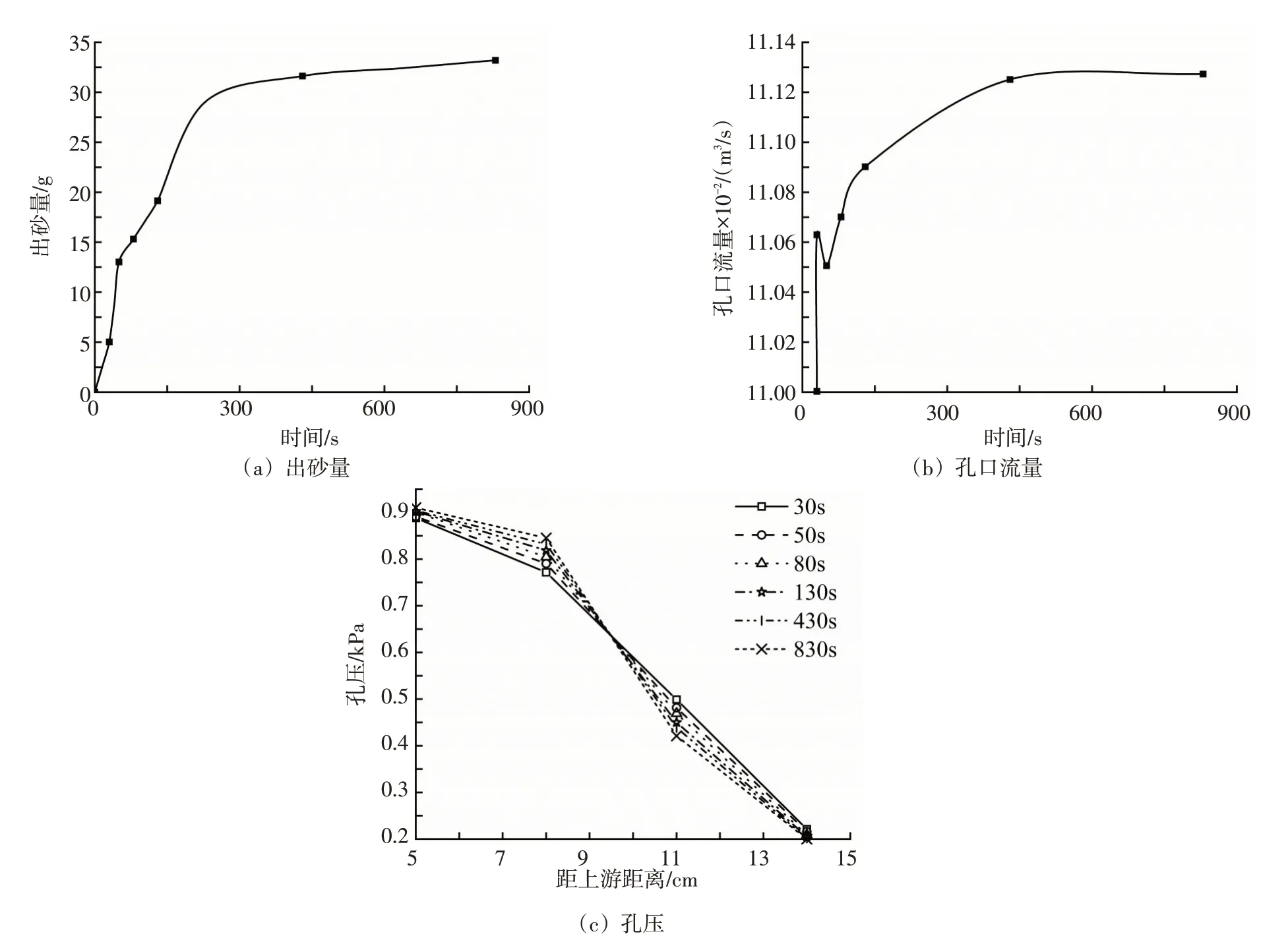
图11 室内模型试验数据

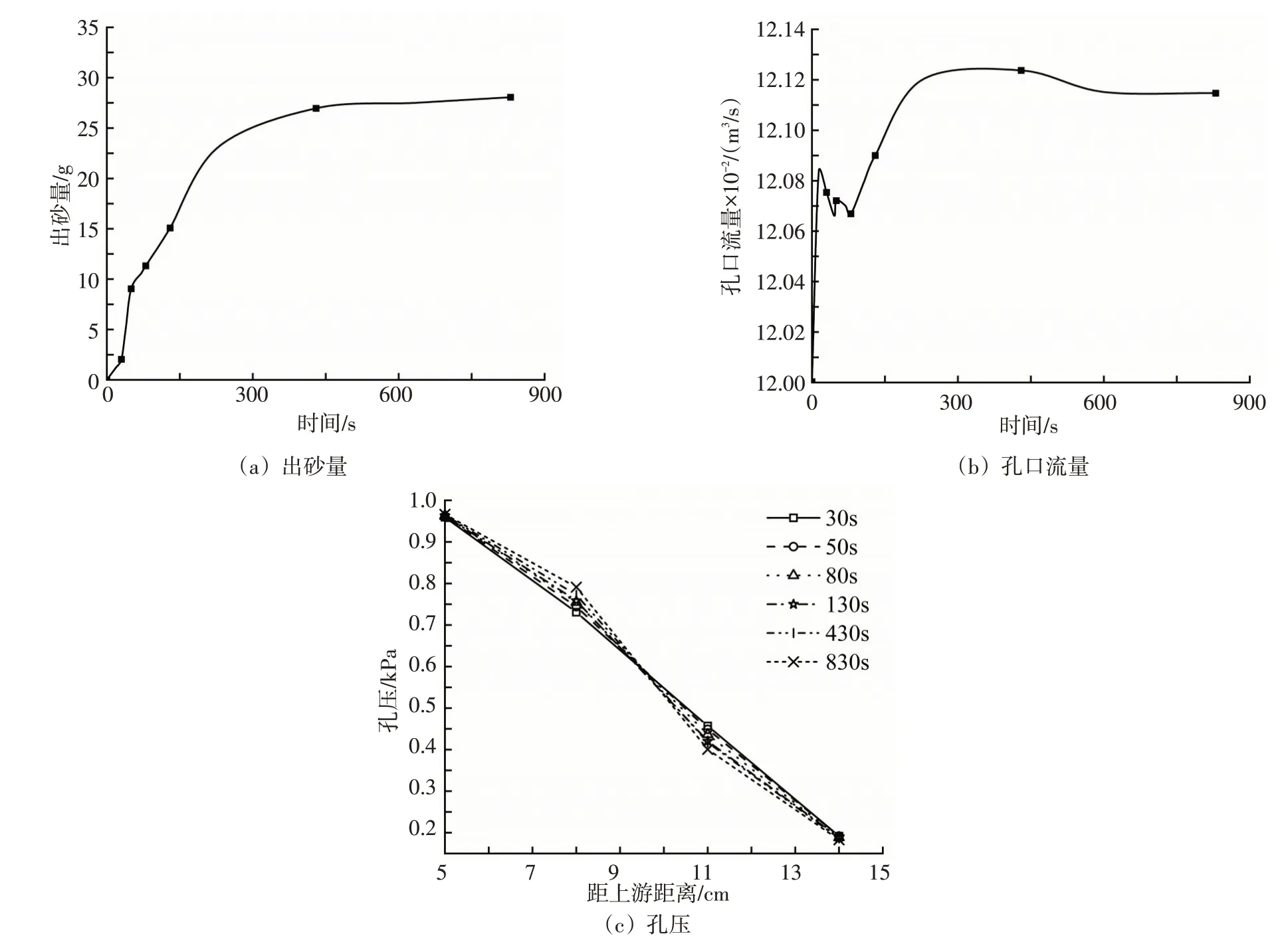
图12 重构土样数值模拟试验数据

利用透明土技术（见3.1节）测量试验模型各切片孔隙率的变化数据，结合图10（a）（b）分析得室内试验模型与重构土样模型各切面孔隙率的变化趋势在渗流初期都出现较大波动，在本模型中，随着渗流通路的逐步扩展，各切面的孔隙率变化逐步稳定，由于上游颗粒流入速率小于颗粒流出速率，下游颗粒流入速率大于颗粒流出速率，故渗流通路扩展结束达到稳定后，上游孔隙率终值大于初值，下游孔隙率终值则小于初值；结合图11（a）、12（a）可得室内模型与数值模型的出砂速率在初始阶段都很大，同时均出现波动降低的特征，并且随时间推移逐渐降低至0；结合图11（b）、12（b）可看出室内模型与数值模型的孔口流量都在初始阶段上升很快，随后上升速率均逐渐下降并趋于稳定；结合图11（c）、12（c）可知，距离上游（开孔透水板）6 ～9 cm范围内的孔压均随时间逐渐增大，由此分析早期土体内部管涌通道迅速发展，离上游较近区域内的细颗粒不断往管涌口迁移，同时细颗粒随水流逐渐被带出土体。另外，在430 s至830 s时间段内孔压几乎没有变化，表明试验后期真实土样与重构土样内部细颗粒仅发生微小运移且土体内部基本形成稳定结构，这也同时映证出砂量、孔口流量和孔隙率随时间的变化趋势。

通过图10、图11 和图12 各项数值比对不难发现，由于试验测量误差以及软件对模型切片处理及重构时产生的数据误差，三维重构土样与试验土样在特定时间点或时间段内所表现的各项数值大小并不完全相同。但由上述分析可知，模型试验与数值模拟所得数据在变化趋势上基本相同，同时数据差异并不非常大，因此验证利用PFC3D开展重构土样的管涌细观机理研究是合理可行的。

4 不同工况下管涌细观机理研究

本节基于上述三维重构方法进行颗粒流模拟的可靠性，开展相同水头下不同颗粒级配、不同细料含量和不同颗粒摩擦系数3种工况下的数值模拟，从颗粒间接触力链的角度揭示管涌的细观机理。

4.1 土样分组及参数信息基于陈建生［29］和刘杰［30］等学者对细料含量与管涌发生、发展之间关系的探究、毕忠伟［31］等对摩擦系数的选取研究，根据3种不同工况对用于颗粒流模拟的重构土样进行参数设置及分组，如表3所示，表中内摩擦系数对应骨架颗粒参数，与土体宏观摩擦角意义不同，故取值可能大于1。为避免出现接触冲刷现象，将模型上边界摩擦系数设置为较大值，其余参数选取参考表2。

表3 各工况下土样分组及参数信息一览表

4.2 数值试验结果根据表3 中各土样（H/F）min信息可知，A1 组土样为稳定级配，且在模拟过程中不发生管涌，故本文不对其进行介绍和分析。经颗粒流数值模拟，得到其余各组非稳定级配土样管涌试验数据，图13—15 分别给出各组重构土样细颗粒流失量、孔压与孔口流量随时间的变化规律。

图13（a）表明，A2、A3两组模型细颗粒流失量均随时间逐步增长，最终趋于稳定，不同之处在于A2 组细颗粒流失速率先平缓变化、中间急剧上升最后逐渐下降，而A3 组细颗粒流失速率平缓下降；图15（b）（c）则反映，A2组模型孔口流量随时间呈波动上升最终趋于稳定，而A3组模型初始阶段流速近似直线上升，但随时间逐渐趋于稳定；结合图14（a）（b），A2、A3两组模型孔压自上游至下游均呈现不断下降的趋势，由于靠近上游的细颗粒在水头作用下不断向下游流动，导致上游孔隙率增大，孔隙水承担的水头部分逐渐增大，而下游孔隙率减小，孔隙水承担的水头部分逐渐减小，故A2、A3 两组模型土上、下游孔压差值逐渐增大，为管涌的发展提供水力条件，同时距上游4cm 至管涌口的范围内，任一位置的孔压随时间逐渐减小，表明A2、A3 两组模型土内部管涌现象逐渐衰弱。

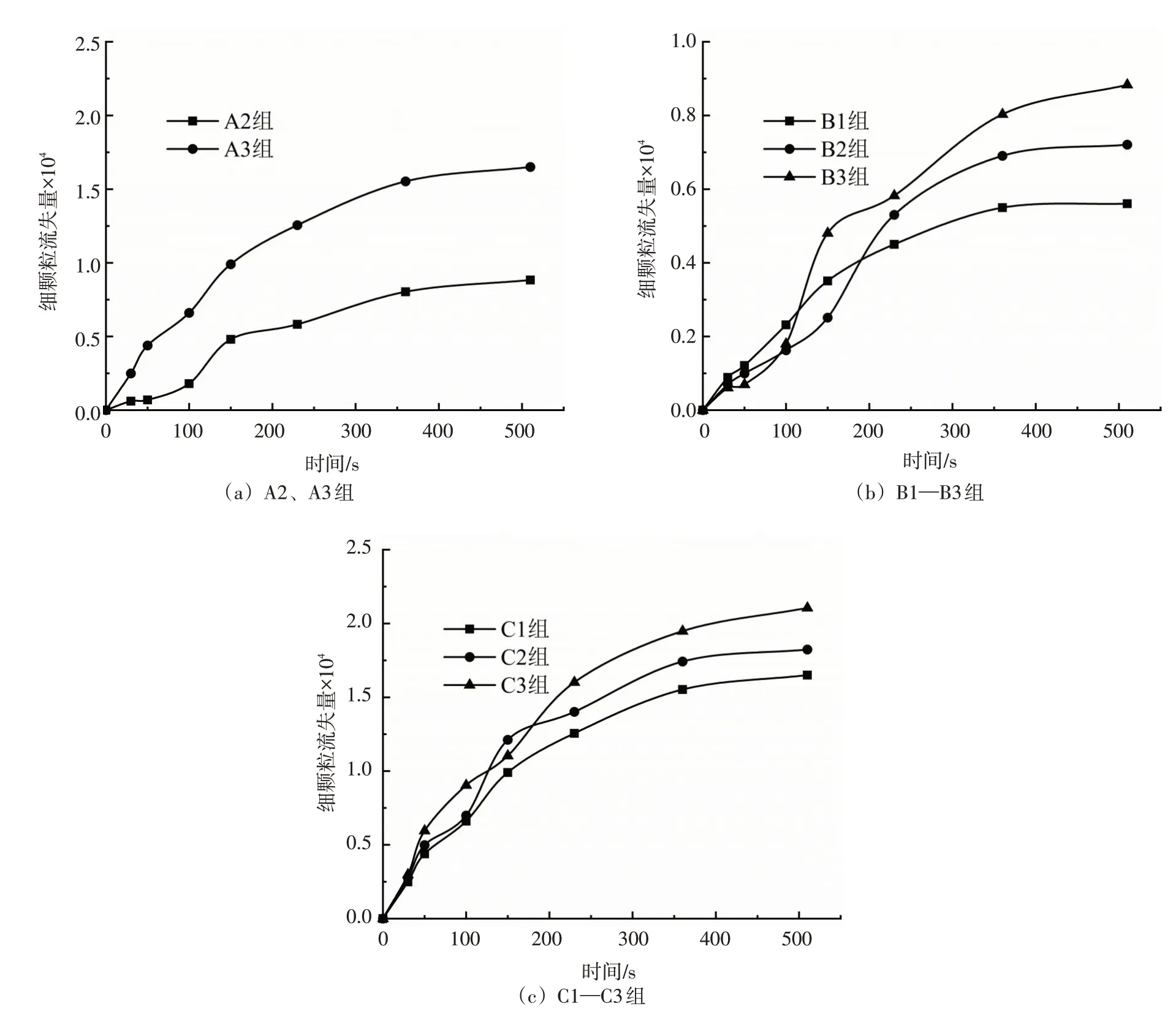
图13 各组土样细颗粒流失量随时间变化规律

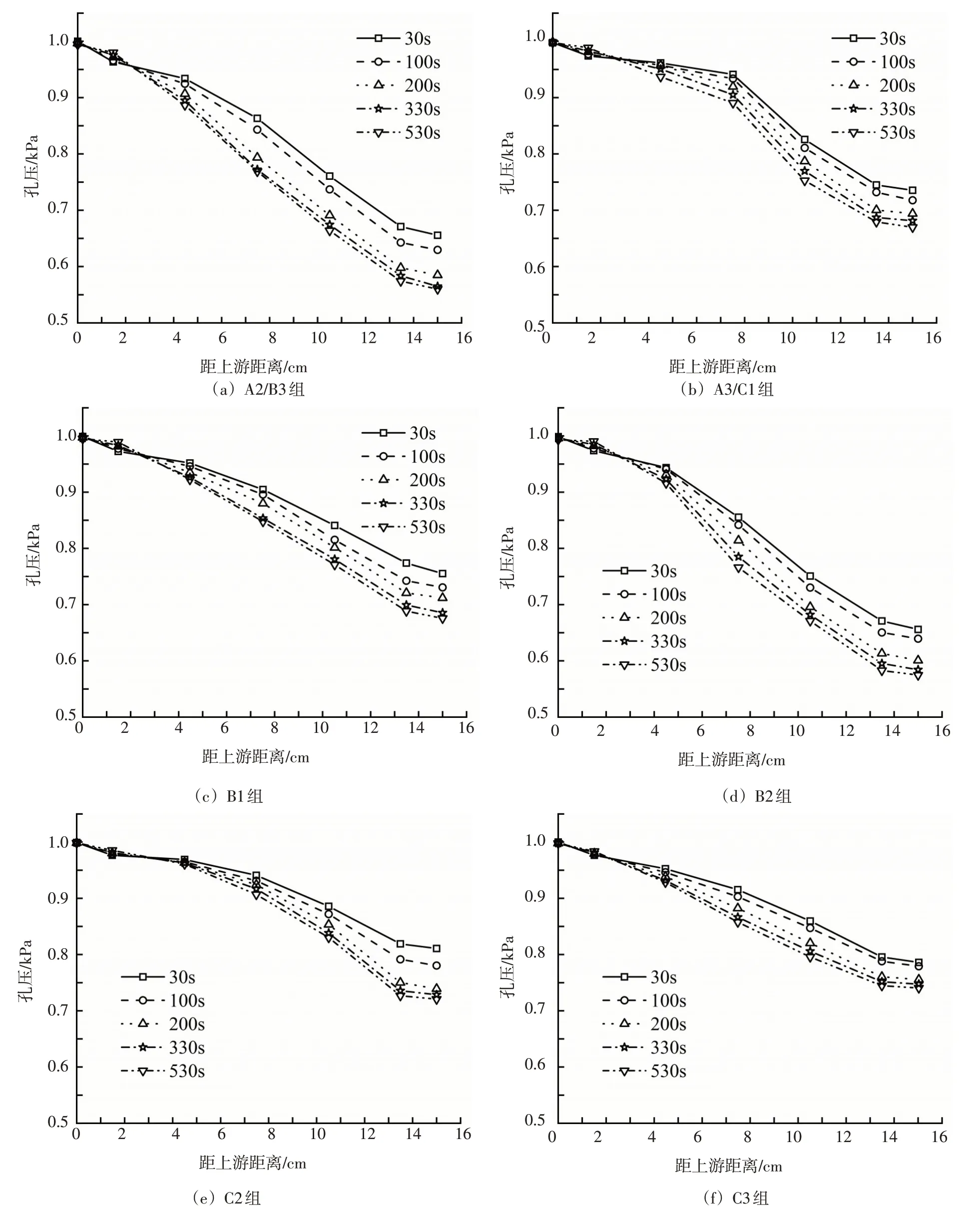
图14 各组土样孔压随时间变化规律

图15 各组土样孔口流量随时间变化规律

图13（b）表明，B1、B2、B3 各组土样颗粒流失量随时间变化趋势大体一致，模拟过程中均出现管涌衰弱现象。不同之处在于，细颗粒流失速率在0 ～100 s 时间段内随细料含量增加而降低，B2、B3 组细颗粒流失速率与B1 组相比还呈现出一种波动降低特征，其中B3 组波动现象最为明显；另外随着细料含量的降低（B3→B2→B1），孔口流量随时间变化规律由“波动式”上升变为“平滑式”上升。

图13（c）表明，C1、C2、C3各组土样颗粒流失速率随时间变化趋势大体一致，细颗粒流失速率及流失量随着摩擦系数的降低而增加，C2、C3组的细颗粒流失速率与C1组相比还呈现出一种波动特征，其中C3组波动现象最为剧烈。同时在模拟过程中，3组土样也都出现明显的管涌衰弱现象。不同之处在于初期阶段，各组孔口流量的增长速率随着摩擦系数的降低而提高，其中C3组最大，C1组最小。

4.3 试验结果分析下面从力链结构网络的角度阐述不同颗粒级配、细料含量和颗粒摩擦系数对管涌发生发展的影响。

图16给出10 s时刻各组重构土样内部细颗粒、弱接触（粒间接触力数值位于0.5至1倍平均接触力区间）与力链之间的关系。

4.3.1 颗粒级配对管涌发生发展的影响 A1、A2、A3三组不均匀系数均大于10，其中A1组不均匀系数为10.4，级配良好且较为连续，孔隙喉径较小，表明细颗粒流失能够被大颗粒阻挡，因此A1组（H/F）min大于1且不发生管涌；A2、A3两组不均匀系数分别是16.7、17.3，级配良好但不连续（中间粒径缺失较多），孔隙喉径较大，表明绝大多数细颗粒流失不能够被大颗粒阻挡，因此A2、A3组（H/F）min小于1且发生管涌。此外，由于粗、细料粒径大小设置的不同，导致A3组级配相对于A2组级配较连续，故A3组有少部分细颗粒流失被大颗粒阻挡，且A3组（H/F）min值也略大于A2组。

本节从力链总数、弱接触与力链结构关系两个角度阐述不同颗粒级配致使颗粒流失速率、孔口流量变化趋势不同的原因，进而揭示颗粒级配对管涌发生发展细观机理的影响。图17给出30 s、80 s、230 s、430 s时刻A2、A3组土样删去细颗粒后力链总数的变化情况。

在颗粒物质力学中，颗粒物质受到的外力基本由力链承担，弱接触虽不构成力链，但对力链网络的稳定有重要影响。对于A2 组土样：由图17（a）知，力链总数因细颗粒删除发生明显变化，表明部分细颗粒也参与力链网络构成，粗颗粒之间非完全接触支撑，图16（b）（d）进一步证明该结论；由图16（a）（c）推证细颗粒参与构成大量弱接触，因此当参与构成弱接触的细颗粒发生流失后，将造成力链位置上的颗粒松动迁移，使得该力链的影响范围出现一定变形，期间不可避免会对已形成的渗流通路造成影响，继而力链随时间发生调整导致图13（a）中的颗粒流失速率波动，渗流通路便也因此不断调整导致孔口流量呈现图15（b）中的“台阶式”上升。对于A3 组土样：由图17（b）知，力链总数在细颗粒删除后降幅很小，表明该组力链主要由粗颗粒构成，图16（f）（g）则更加直观地论证该结论；由图16（e）知，接触力链附近分布弱接触数目极少且大多为模型与墙体边界之间的接触，表明水头几乎全部由力链承担；对比图16（f）（g）分析得，土样内部在管涌侵蚀过程中很难因细颗粒流失出现区域性“扰动”。因此，A3 组试验的颗粒流失速率呈现图13（a）中单调衰减趋势且收敛速度较快，内部管涌通路随细颗粒流失不断扩展，孔口流速呈现图15（c）中平滑缓慢上升趋势。

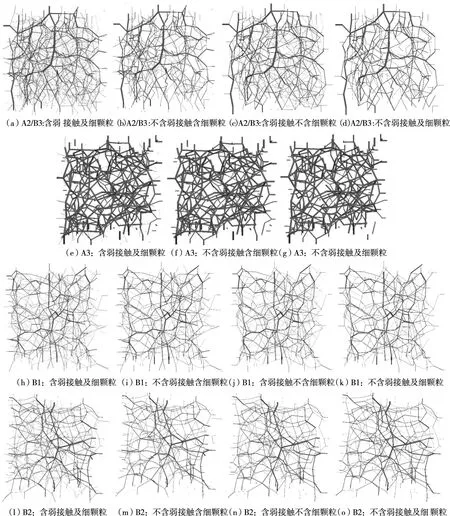
图16 各组细颗粒、弱接触与力链关系

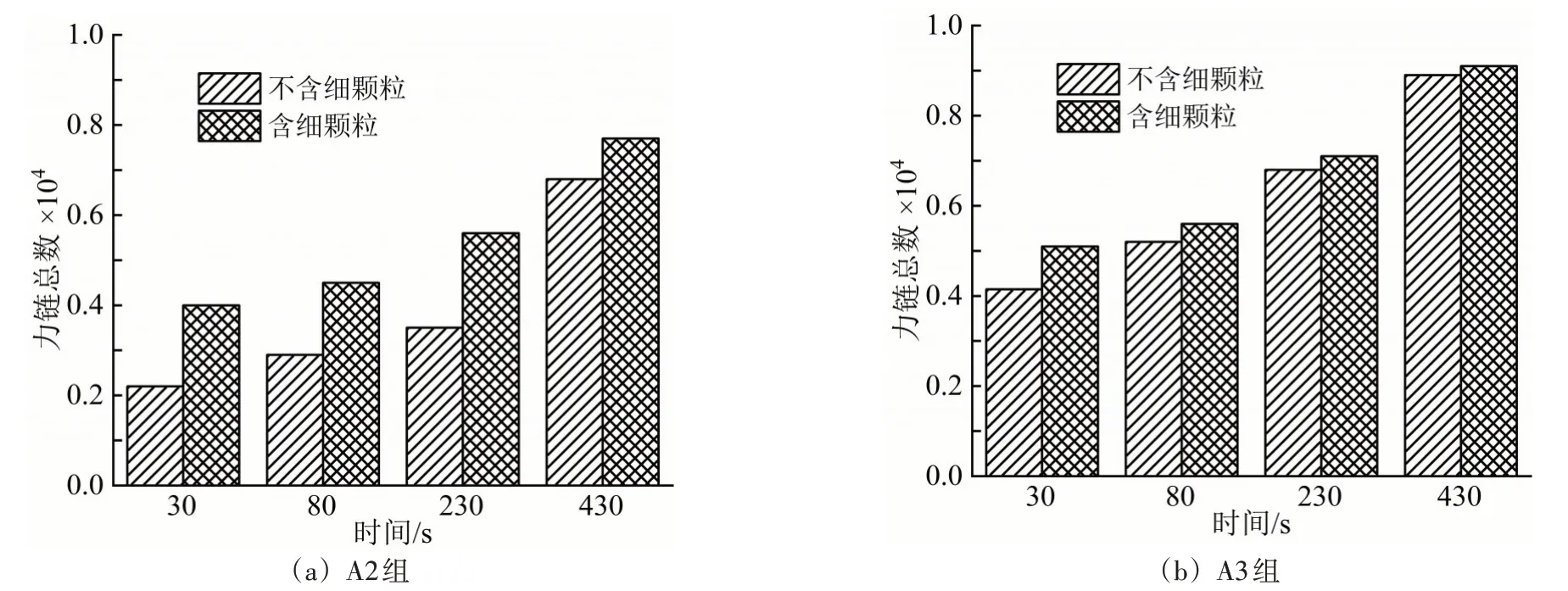
图17 力链总数随时间变化情况

4.3.2 细料含量对管涌发生发展的影响 图18—20分别给出管涌模拟初始阶段，B1、B2、B3各组细颗粒参与构成力链和弱接触的比例、力链总数随时间的变化规律，进而阐述图13（b）中细颗粒流失速率变化规律与图15（a）（b）中孔口流量变化规律。

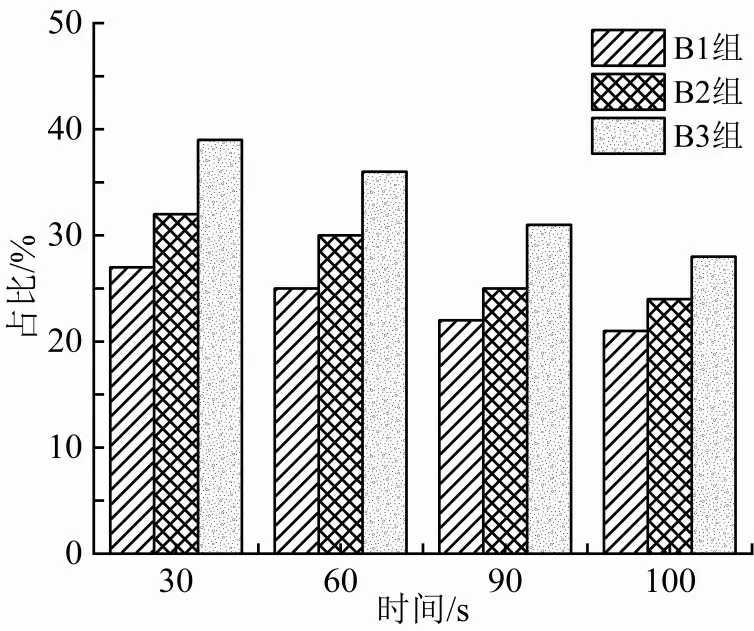
图18 细颗粒参与构成力链比例

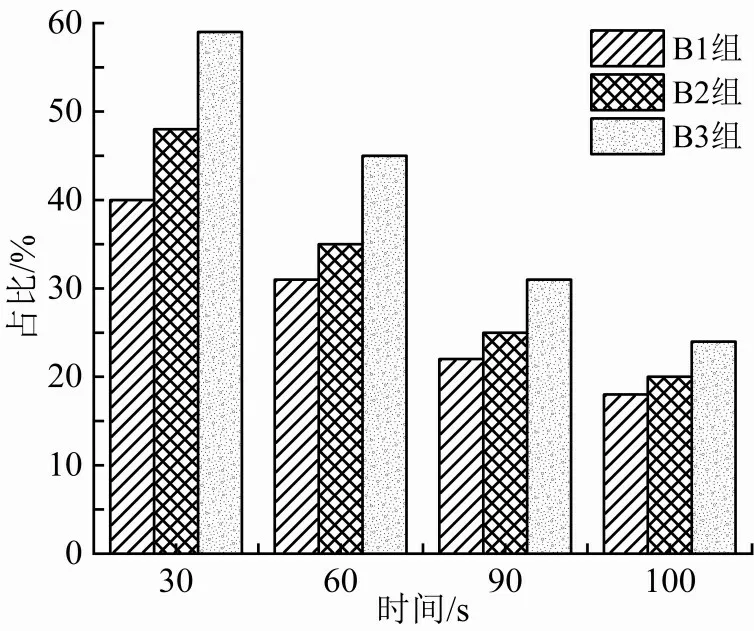
图19 细颗粒参与构成弱接触比例

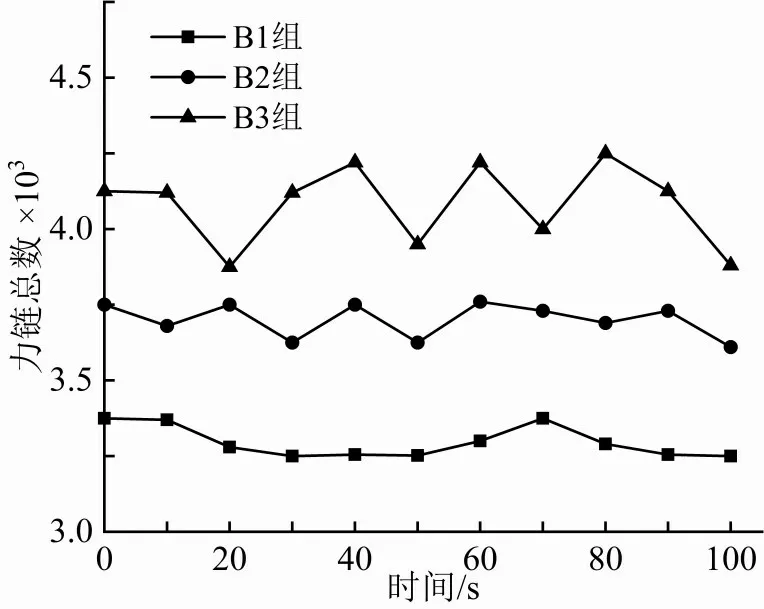
图20 力链总数随时间的变化规律

由图18、20分析可得，细料含量越大，参与构成的力链数和弱接触数比例越大，土体中力链总数在初始阶段波动幅度和频率也越大，故细料含量高的土体（B3组）更容易因细颗粒流失引起结构失稳并出现力链断裂与重构现象，图16（i）与（k）、（m）与（o）、（b）与（d）则更加直观地说明该现象。因此细料含量的增加使细颗粒逐渐填满粗颗粒间孔隙，造成细颗粒更多的参与力链结构构成，继而形成相对稳定结构，以致在模型初始阶段细颗粒难以被水流带出土体，继而初始阶段内细颗粒流失速率随细料含量增加而降低。由图19 可知，细料含量越大，参与构成的弱接触数比例越大，图16（h）与（j）、（l）与（n）、（a）与（c）进一步论证了该结论。

由4.3.1节分析知，细颗粒流失会对已形成的渗流通路造成影响，而细料含量高的土体更容易因细粒流失引起结构失稳，继而力链随时间发生更为频繁的调整且幅度较大，导致B2、B3组细颗粒流失速率与B1组相比呈现出一种波动降低特征，且B3组波动现象最为明显。此外，随着细颗粒发生流失，细料含量低的土体因其内部细颗粒未能填满粗颗粒孔隙，力链结构主要由粗颗粒构成（内部结构更为疏松），细颗粒很容易在粗颗粒形成的孔隙通道中随水流发生运移，宏观上表现为渗透性增强，即渗透系数随着细颗粒的流失不断增大。因此细料含量由大到小，对应孔口流量从“波动式”上升转变为“平滑式”上升（图15（a）（b））。

4.3.3 颗粒摩擦系数对管涌发生发展的影响 本节基于力链中细颗粒数目、力链总数与力链方向分布概率3个角度揭示颗粒摩擦系数对C1、C2、C3各组土样细颗粒流失量与孔口流量的影响机理。图21—23分别给出了力链中细颗粒数目、力链总数与力链方向分布概率随时间的变化规律。

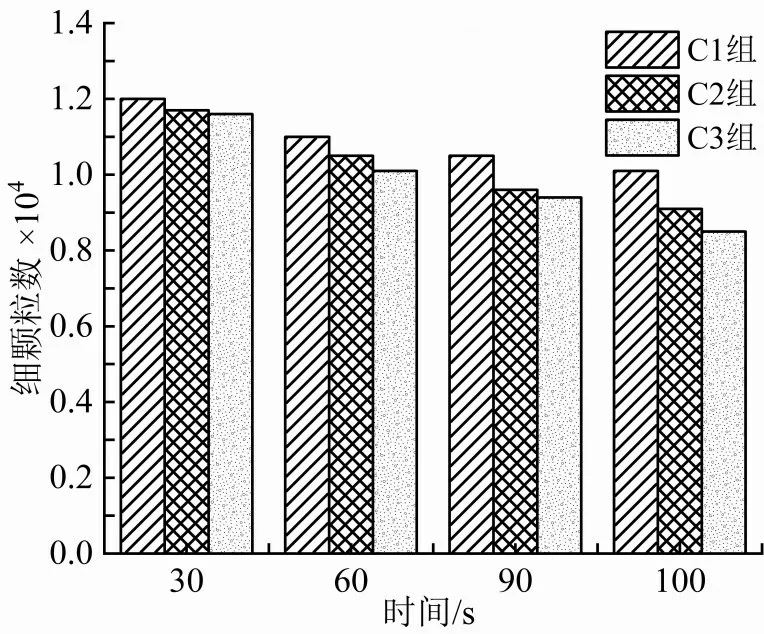
图21 模型初期力链中细颗粒数目

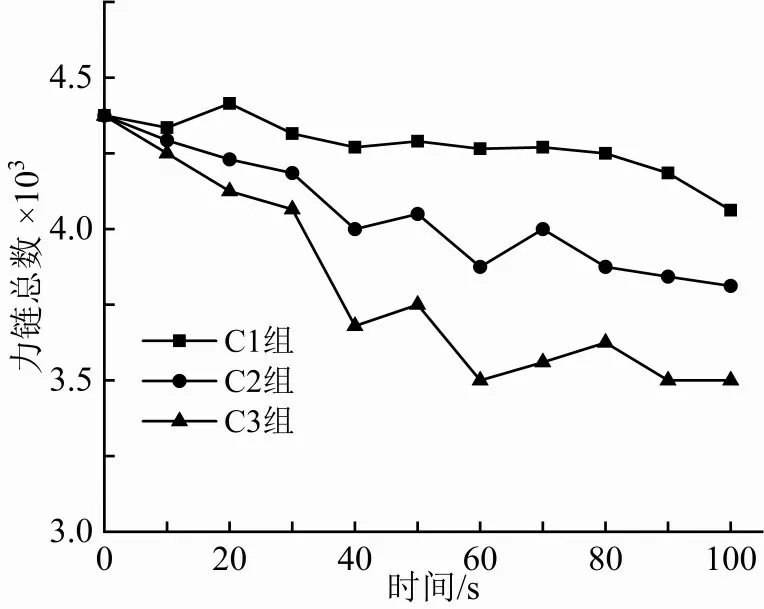
图22 力链总数随时间变化规律

本节各重构土样生成时，在PFC3D程序设置的随机数相同，即C1、C2、C3各组土样初始内部结构相同，进而不同摩擦系数土样内，细颗粒参与力链构成的情况也相同。结合图21、22分析得，随摩擦系数提升，土样内部力链中所含细颗粒数量降幅变小，力链总数波动也趋于平稳，表明力链发生断裂与重构的频率降低，即力链结构网络的稳定性得到提高。因此，摩擦系数降低使得细颗粒更加容易因渗流力的作用流失，继而细颗粒参与构成的力链发生断裂，导致该力链影响的区域出现变形，此期间力链随时间调整的过程即为图13（c）中细颗粒流失量产生波动的原因。

由图23可知，随着摩擦系数的提升，模型初期阶段轴向±30°范围内，参与力链构成的细颗粒越发不易因渗流力作用发生流失，且随时间的推移，土样内部力链迅速向该角度范围内集中以抵抗渗流力，同时随着摩擦系数的提升其稳定性也相应提高，所以总体上来看，轴向±30°范围内的力链方向概率随摩擦系数增加而增加。于是也进一步说明粗颗粒摩擦系数的提升使得土体细颗粒流失量减小，从而使得其所形成的渗流通路扩展得更慢，即渗透系数增加得更慢，故图15（c）中摩擦系数越大的土样（C1组），孔口流量增长速率和孔口流量上限越小。

5 结论

本文基于透明土技术与颗粒流方法联合开展管涌发生、发展的细观机理研究，从颗粒间接触力链重构与破坏的角度揭示颗粒级配、细料含量和颗粒摩擦系数三种不同因素对管涌发生、发展的影响，进而为管涌细观机理的研究提供一条新的分析途径。主要结论如下：

（1）通过自行研制的透明土和可视化模型试验平台，能获取透明土样的二维切片集合，基于MRI 原理，借助Avzio 软件可实现对其三维重构，同时本文将重构模型导入PFC3D中建立相应的颗粒流模型，通过比对模型试验与颗粒流模拟结果验证PFC3D程序开展重构土样管涌数值模拟研究的可靠性。

（2）（H/F）min≥1.0时，土样为稳定级配，模拟过程中不发生管涌；（H/F）min＜1.0时，土样随着该值的减小由稳定级配转变为不稳定级配，且该值越小越不稳定，细颗粒参与构成力链数、弱接触数也因此越多，粗颗粒由完全接触转变为非完全接触，同时力链更容易因细颗粒流失发生破坏与重构，导致细颗粒流失速率产生波动，孔口流量由“平滑式”上升转变为“台阶式”上升。

（3）细料含量越大，参与构成的力链数和弱接触数比例越大，土体中力链总数在初始阶段波动幅度和频率也越大，继而细颗粒流失速率波动降低的特征更加明显；随着细颗粒发生流失，细料含量低的土体因其内部细颗粒未能填满粗颗粒孔隙，力链结构主要由粗颗粒构成，细颗粒很容易在粗颗粒形成的孔隙通道中随水流发生运移，宏观上表现为渗透性增强，渗透系数随着细颗粒的流失不断增大。因此细料含量由大到小，对应孔口流量从“波动式”上升转变为“平滑式”上升。

（4）摩擦系数的提升有助于增强土体内部已形成力链结构的稳定性，并延缓管涌发展初始阶段细颗粒流失量，特别当细颗粒参与力链构成时，摩擦系数的提升对土体稳定性的积极效果更为明显。