基于最优光伏阵列重构的电网调频策略研究

何廷一，李胜男，陈亦平，吴水军，沐润志，何 鑫，杨 博，曹璞璘

基于最优光伏阵列重构的电网调频策略研究

何廷一1，李胜男1，陈亦平2，吴水军3，沐润志3，何 鑫1，杨 博4，曹璞璘4

(1.云南电网有限责任公司电力科学研究院，云南 昆明 650200；2.中国南方电网电力调度控制中心，广东 广州 510663；3.云南电力试验研究院(集团)有限公司, 云南 昆明 650051；4.昆明理工大学电力工程学院，云南 昆明 650500)

为实现光伏电站功率输出最大化以及功率输出与调频(FR)信号之间的功率偏差最小化，提出了一种新型光伏电站最优阵列重构(OAR)模型。为快速获取最优Pareto前沿，采用了一种寻优性能高效的多目标黑猩猩优化器(MOBO)。采用了一种多准则妥协解排序法(VIKOR)的决策方法，从所获取的Pareto前沿中确定最佳折衷解。为验证所提出的OAR多目标优化的有效性，在局部阴影条件(PSC)下，对10×10的网状结构(TCT) PV阵列进行了固定FR信号和时变FR信号的两个案例研究。仿真结果表明，与无优化相比，所提方法可以明显减小两个目标函数的功率偏差。特别是，时变FR信号下，所获得的功率偏差仅为无优化的51.10%和64.45%。

最佳阵列重构; 光伏电站; 电网调频; 多目标黑猩猩优化器

0 引言

当今世界能源紧张，可再生能源由于其取之不尽、用之不竭的特性，研究和发展已经受到了广泛关注，并逐渐替代大多数化石燃料[1-4]。其中，太阳能被认为是这些能源中最有潜力的一种。然而，由于日照不均、温度梯度和局部阴影(Partial Shading Condition, PSC)[5-6]等多种动态环境条件的影响，光伏(Photovoltaic, PV)阵列在实际工程中的大规模应用仍存在一些亟需解决的问题。例如，PSC会造成PV阵列的失配损耗和功率损耗，从而导致PV阵列性能降低。产生PSC的原因主要是云层遮蔽、建筑物阴影和灰尘覆盖等。为减少PV阵列的失配损耗和功率损耗，已设计出诸如串并联结构、网状结构(Total-Cross-Tied, TCT)和桥式结构等拓扑连接形式[7]。由文献[8]可知，PSC下TCT阵列的性能均优于其他拓扑结构。但PSC对其的影响不可忽略，基于此，文献[9]提出了三种基于物理阵列重构形式的技术，包括物理重定位、电气阵列重构(Electrical Array Reconfiguration, EAR)和电气重布线，其旨在通过平衡TCT阵列上的阴影来减轻失配损耗。

另外，根据PV阵列重构之后电气连接是否改变，PV阵列重构可分为静态重构和动态重构。在静态重构中，所有模块的物理位置在PSC下都是固定的，这意味着重构后，PV阵列电气连接保持不变。静态重构主要利用电气重布线技术来提高PSC下的功率输出，包括固定电气重构法[10]、列索引法[11]和数独法[12]。与其他两种重构方法相比，数独法被认为是电气重布线技术中最有效的方法[13]。除电气重布线外，还提出了许多物理重定位技术，例如魔方重构[14]、固定电气连接[15]和奇偶重构等[16]。研究表明，基于魔方重构的物理重定位技术可以避免使用复杂的最大功率跟踪算法，并能提供卓越的性能。

与静态重构不同，动态重构可以依据实时的阴影变化，调节开关装置，从而动态地改变其电气连接。相较于静态重构，动态重构不需要花费大量的劳动力和复杂的应用。近年来，许多算法已成功应用于EAR技术，如RBF神经网络算法[17]、粒子群优化算法[18]、蚱蜢优化算法[19]、多目标灰狼算法[20]、标准遗传算法[21]、海洋捕食者优化算法[22]和Rao优化算法[23]等。

然而，现有的PV阵列重构研究并未考虑调频(Frequency Regulation, FR)信号的影响[24]。因此，本文建立了一种新型的PV阵列最优阵列重构(Optimal Array Reconfiguration, OAR)参与电网调频的方法，以提升整个区域电网的动态响应性能。其以最大化功率输出和最小化功率输出与FR信号之间的功率偏差为目标。为快速获取该多目标优化函数的最优Pareto前沿，本文采用了一种新颖的高效多目标黑猩猩优化器(Multi-objective Bonobo Optimizer, MOBO)，同时采用了一种多准则妥协解排序法(VIseKriterijumska Optimizacija I Kompromisno Resenje, VIKOR)[25]，以便从获取的Pareto前沿中确定最佳折衷解。

1 光伏电站最优阵列重构数学模型

1.1光伏阵列建模

PV阵列通常由多个串/并联的PV模块组成，而这些PV模块又由多个串/并连的PV电池组成。图1给出了常用的单二极管PV电池模型[26]。应用基尔霍夫电流定律(Kirchhoff’s Current Law, KCL)可以计算出PV电池的输出电流，如式(1)所示。

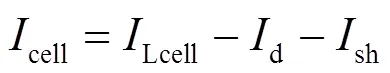
图1 单二极管PV电池等效电路

Fig. 1 Equivalent circuit of a single-diode based PV cell

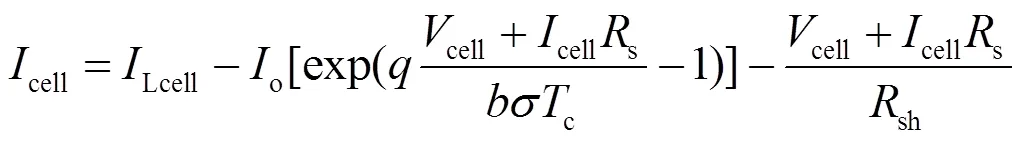
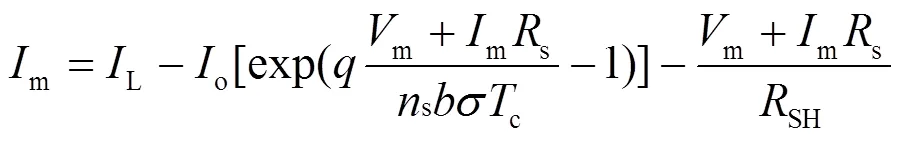
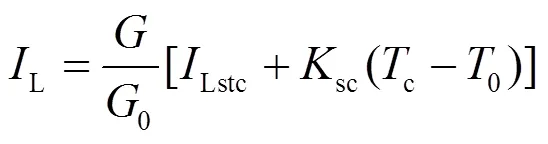
综上所述，如图2所示，由s×p的PV模块所组成的PV阵列，其输出电流可表示为如下形式。

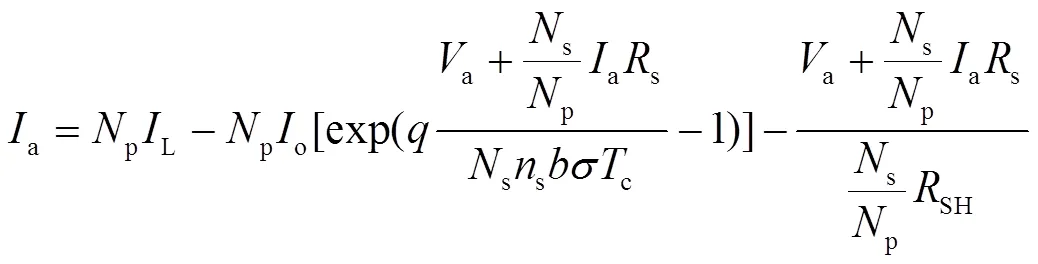
图2 具有Ns×Np PV模块的PV阵列等效电路

Fig. 2 Equivalent circuit of a PV array with Ns×Np modules

1.2 网状结构PV阵列建模

在传统的光伏阵列拓扑结构中，TCT拓扑已被证实，能在PSC下表现出最优异的性能。图3给出了10×10 的TCT连接PV阵列，其所有行都串联连接，每行并联10个这样的连接串。

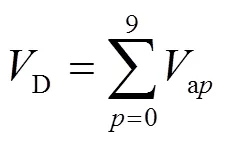
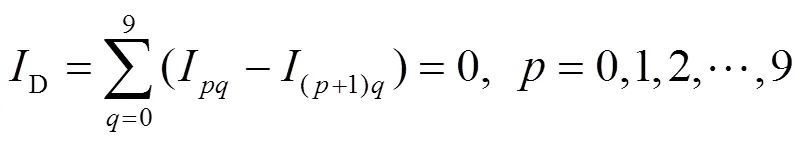
1.3目标函数

本文同时考虑了两个相互矛盾的目标，即最大化功率输出和最小化功率输出与FR信号之间的功率偏差，其旨在提高光伏电站的发电效益，同时帮助平衡电力系统的电力干扰，从而提升整个区域电网的动态响应性能。第一个目标可转换为额定输出功率和平均输出功率之间的功率偏差1最小。第二个目标可转换为FR信号和功率输出之间的功率偏差2最小，同时还考虑了功率输出的峰谷差。因此，可构建目标函数如式(8)所示。

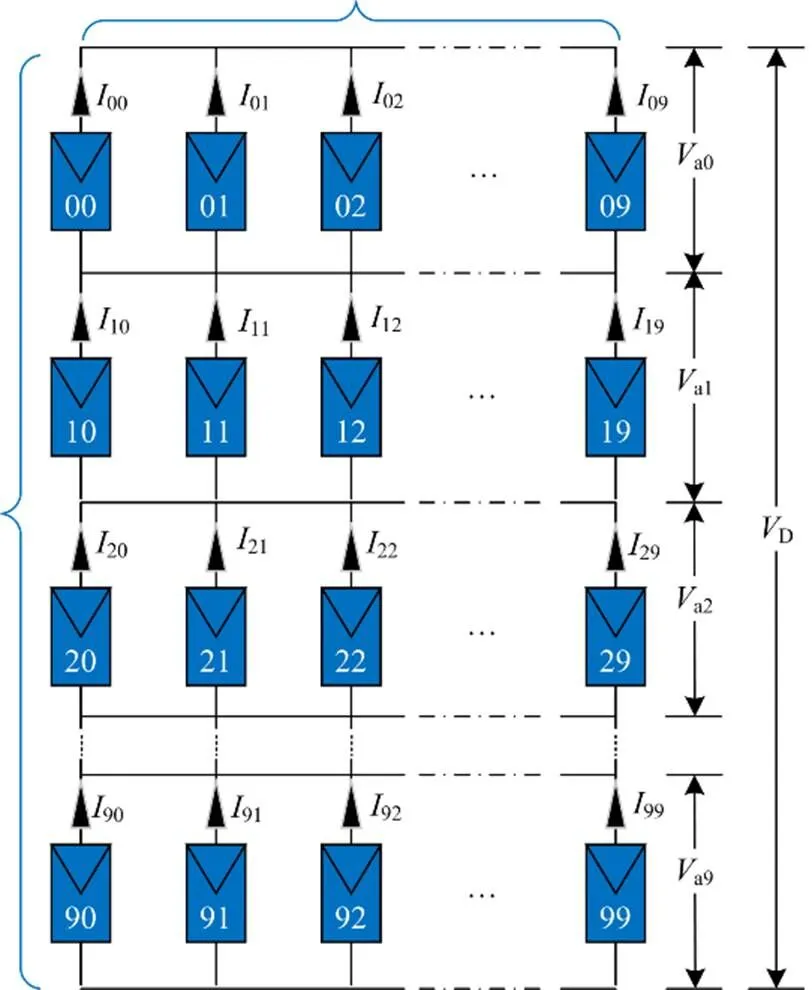
图3 10×10 TCT连接的PV阵列

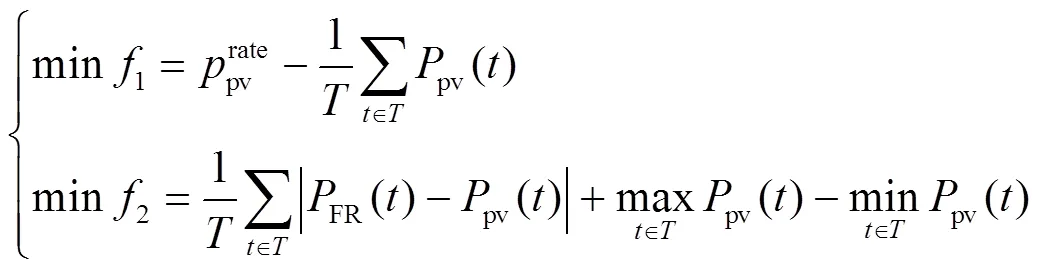
1.4 约束条件

首先，OAR应满足电气开关状态约束，即每个PV阵列只能与同一列中的另一个PV阵列交换所在位置，如式(9)所示。

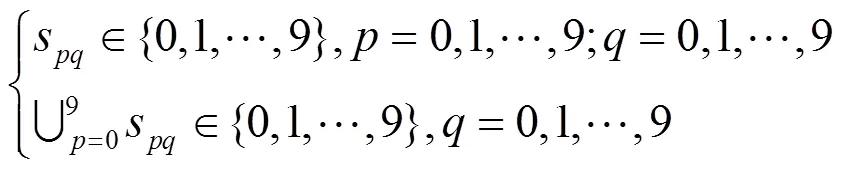
2 针对光伏阵列重构的MOBO和VIKOR设计

2.1 多目标黑猩猩算法设计

黑猩猩优化器(Bonobo Optimizer, BO)是一种智能的自适应启发式优化算法，其灵感来自于黑猩猩的社交行为和生殖策略。黑猩猩遵循裂变融合的社会策略，即黑猩猩通常会分成几个小组进行多种活动，而当需要完成某些特定的活动时，它们又聚集在一起，形成一个群体。

BO与其他启发式算法相似，群体中的每只黑猩猩都被视为算法的一个解，群体中处于主导地位的黑猩猩称为α-bonobo，即算法的最优解。在迭代过程中，当α-bonobo向有利于黑猩猩群体生存和繁殖方向改进时，称为正相位(Positive Phase, PP)，反之，则称为负相位(Negative Phase, NP)。当处于PP时，种群中的其他黑猩猩向α-bonobo靠近，而在NP的情况下，黑猩猩会尝试远离α-bonobo，如图4所示。这种独特的策略被应用到BO中，以提高算法搜索机制的效率。值得注意的是，在黑猩猩群体中，α-bonobo的地位不是一成不变的，即不能保证α-bonobo作为领导者的状态永远保持下去。如果在迭代过程中发现当前黑猩猩比α-bonobo表现更为优秀，则将α-bonobo的状态赋予当前黑猩猩。

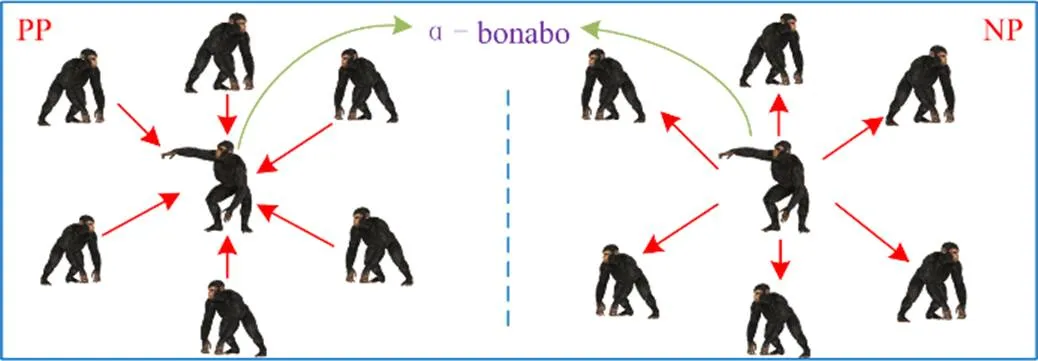
图4 BO算法原理图

Fig. 4BO algorithm principle diagram

下面介绍BO的工作方式，步骤如下：

1) 初始化算法参数

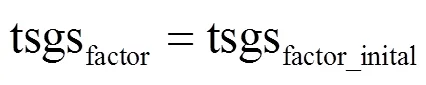
2) 使用裂变融合技术选择与th-bonobo交配的th-bonobo

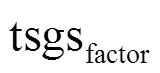
式中，表示黑猩猩的种群大小。

3) 使用不同的交配策略创建新的黑猩猩个体

4) 更新黑猩猩群体和α-bonobo

5) 更新控制参数

如果在迭代过程中发现新获得的α-bonobo比之前的α-bonobo更好，则按如下方式更新算法参数。

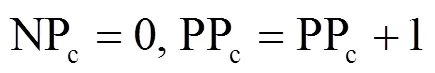
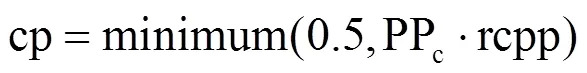
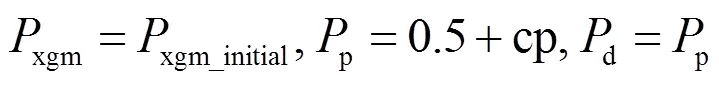
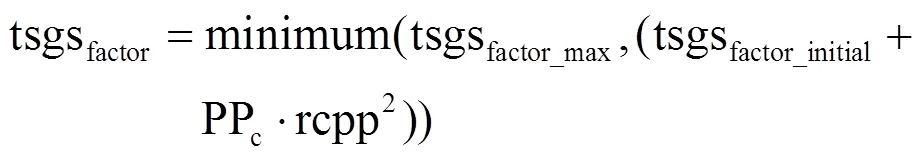
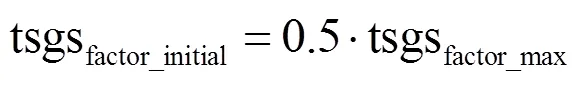
否则，按如下方式更新算法参数：

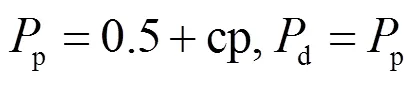
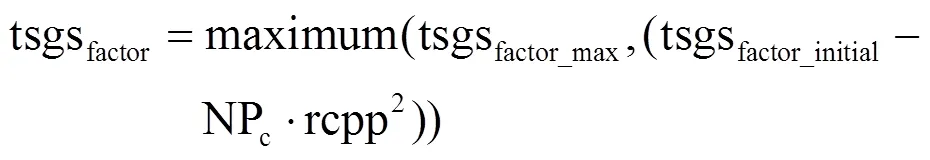
多目标黑猩猩优化器(Multi-objective Bonobo Optimizer, MOBO)启发自NSGA-II算法，继承了NSGA-II非支配排序的概念，通过NSGA-II算法为其种群分配等级，并进行拥挤距离计算[27]，然后将更新后的种群替换BO算法中的种群，依次进行迭代，从而获取非支配解的Pareto前沿，具体步骤如下：

(1) 基于NSGA-II排序方案对规模为的种群进行非支配解排序。首先从现有的支配解中找到所有非支配解，将其设为等级1。然后，忽略这些已标记的非支配个体，再次从现有的支配解中寻找非支配解，并将其分配为等级2。依次类推，直到整个种群分配完成。

(2) 进行拥挤距离计算。拥挤距离是第个解决方案的相邻解决方案(即第-1个和第+1个解决方案)形成的矩形周长。拥挤距离的计算保证了种群多样性。

(3) 基于前面获得的非支配解排序和拥挤距离，进行拥挤距离比较。如果两个个体的非支配排序不同，则序号较小的个体获胜；如果两个个体在同一分配等级，则拥挤距离较大的个体获胜。

(4) 将新创建的子代黑猩猩群体与父代合并组成大小为2的种群，并基于上述非支配解排序和拥挤距离比较，从组合种群2中确定大小为的种群。

接下来，我们将介绍MOBO和OAR之间的设计过程。

2.1.1 约束处理

为了满足等式(9)中的电气开关约束。本文为每列PV阵列分配0到9之间的不同数字。在这项工作中，将根据当前解的顺序重新排序这些数字。对于第列，可以按以下方式更新该列PV阵列的序号。

2.1.2 适应度函数

MOBO的适应度函数设计如式(23)所示。

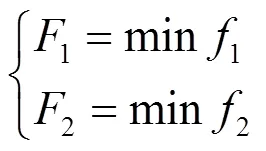
值得注意的是，在优化过程中，式(23)需要满足式(9)和式(22)中的约束条件。

2.2 VIKOR设计

基于VIKOR，可以从MOBO所获得的Pareto前沿中确定最佳折衷解。VIKOR的设计过程如下所示。

步骤1) 根据所获得的Pareto前沿确定正理想解和负理想解，如下式所示。

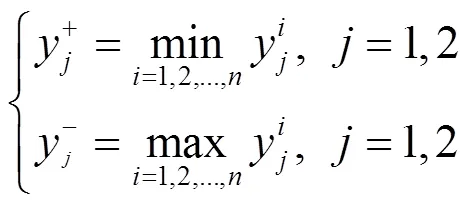
步骤2) 计算每个备选Pareto解的群效用值和个体遗憾值，如下式所示。

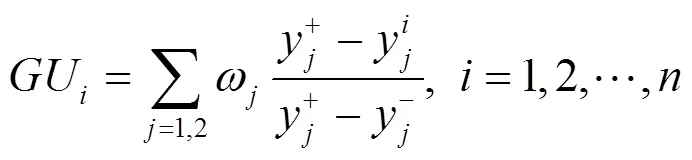
步骤3) 计算每个备选Pareto解的综合评价值，如下式所示。

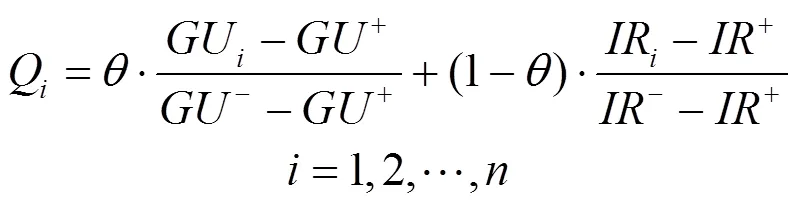
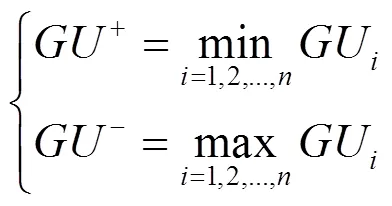
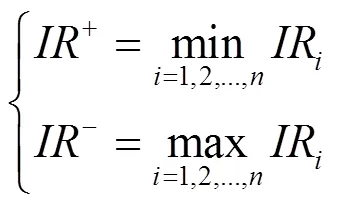
步骤4) 根据综合评价值确定最佳折衷解，如式(31)所示。

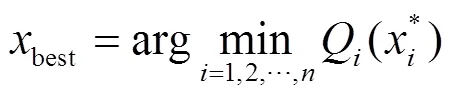
2.3执行程序

表1给出了针对OAR的MOBO和VIKOR的执行过程，其中，表示MOBO的第次迭代，而max是其最大迭代次数。

表1 针对OAR的MOBO和VIKOR的具体执行过程

3 算例分析

本文引入了具有30个相同子系统的30 MW PV电站，以评估所提方法的性能，每个子系统均由10×10的TCT PV阵列组成，其参数取自参考文献[28]，其中光伏模块的主要参数详见表2。所有PV阵列的工作温度均设置为25 ℃，每个子系统在15 min内的辐照度分布如图5所示。

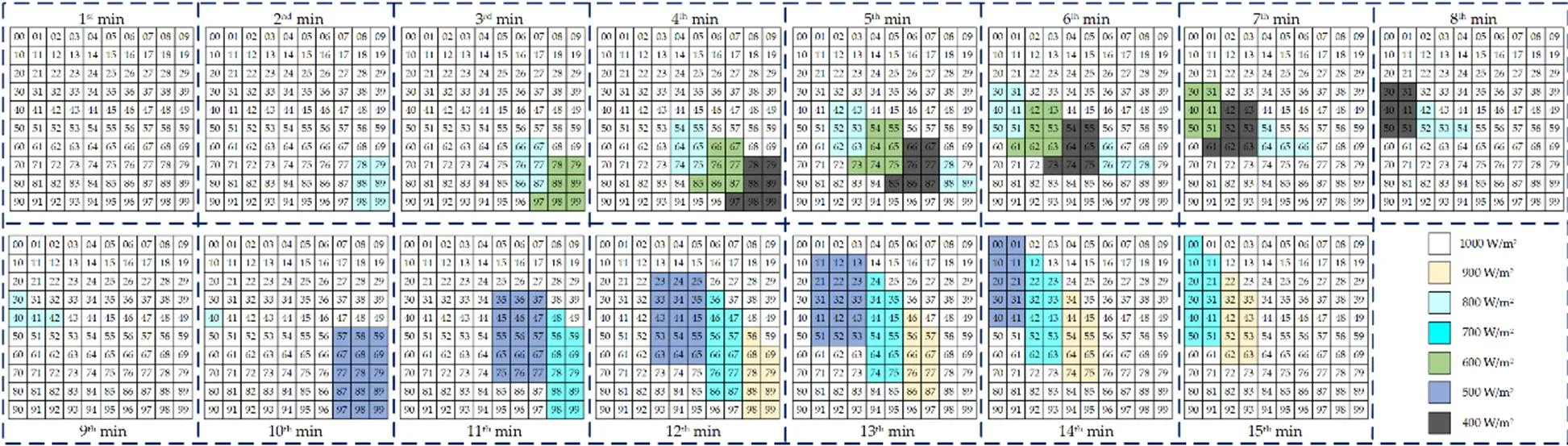
图5 PV电站每个子系统的辐照度分布

表2 PV模块的主要参数

3.1 恒定调频信号

中阴影区域(参见图5)被有效地分配到了不同行，使得不同行之间的电流差显著减小，极大地提升了PV阵列的输出功率。图7给出了经MOBO所获得的最佳Pareto前沿和VIKOR所确定的最佳折衷解。显然，MOBO所获得的Pareto前沿可以在较大范围内平均分配，而VIKOR可以客观地对每个目标函数进行非人为的决策。

图8(a)给出了恒定FR信号下，PV电站的功率输出结果，图8(b)给出了无优化情况和经MOBO优化所获得的功率输出结果。首先，从图8(a)可以看出，与无优化情况相比，通过本文所提方法获得的功率输出更接近FR信号。同时，如图8(b)所示，相较于无优化情况，通过本文所提方法获得的PV电站的输出功率更高。

图9给出了恒定FR信号下，所提方法与无优化情况之间的结果比较。分析表明，相较于无优化情况，通过本文所提方法获得的两个目标函数的功率偏差值更小，可分别减少48.90%和35.55%。

3.2时变调频信号

在此项研究中，设计各种时变的FR信号来评估所提出方法的性能，其中FR信号可以表示为

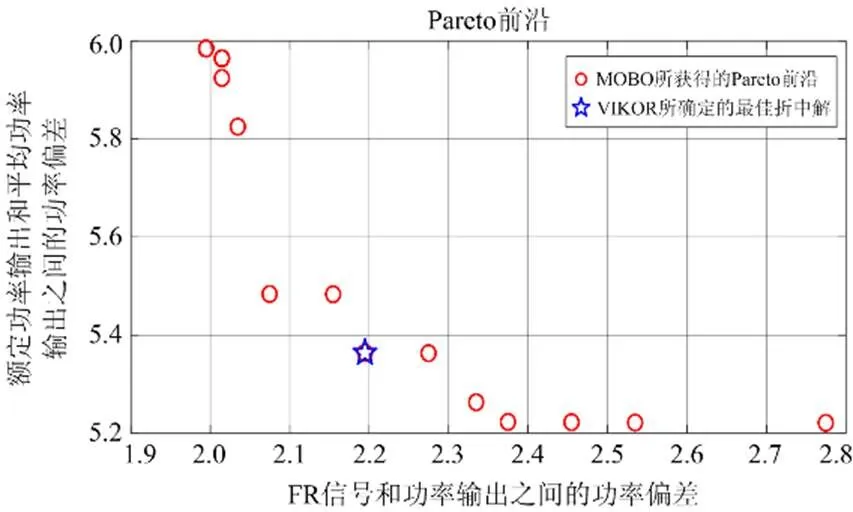
图7 恒定FR信号下，MOBO所获得的最佳Pareto前沿和VIKOR所确定的最佳折衷解

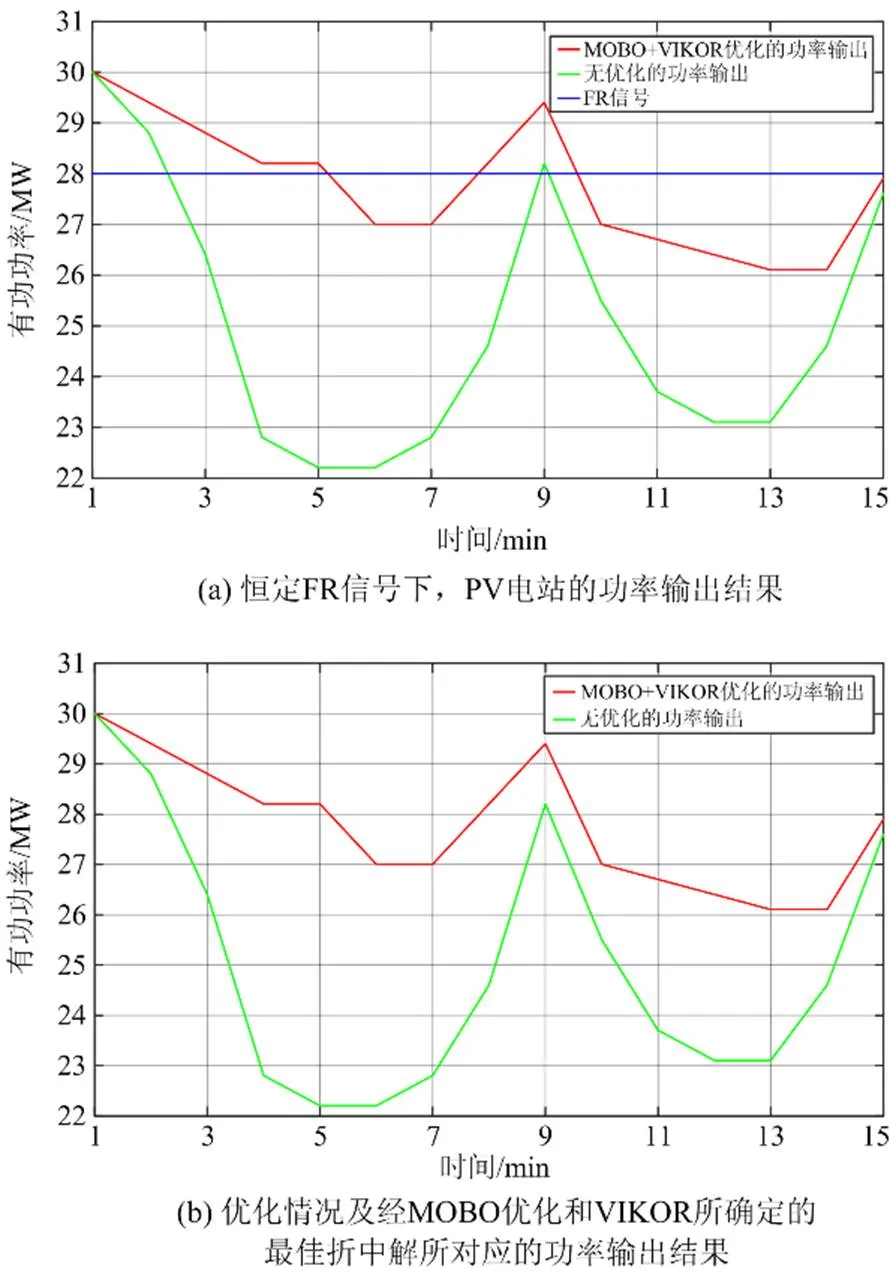
图8 恒定FR信号下，基于所提方法的最佳功率输出及无优化情况下的功率输出

图9 恒定FR信号下，所提方法与无优化情况之间的结果比较

Fig. 9Result comparison between proposed method and that without optimization on a constant FR signal

图10给出了时变的FR信号下，由MOBO所获得的最优Pareto前沿及经VIKOR所确定的最佳折衷解。由图10可知，通过MOBO所获得的Pareto前沿可以有效覆盖两个目标函数的分布范围。此外，VIKOR可以从所获得的Pareto前沿中客观地确定最佳折衷解。

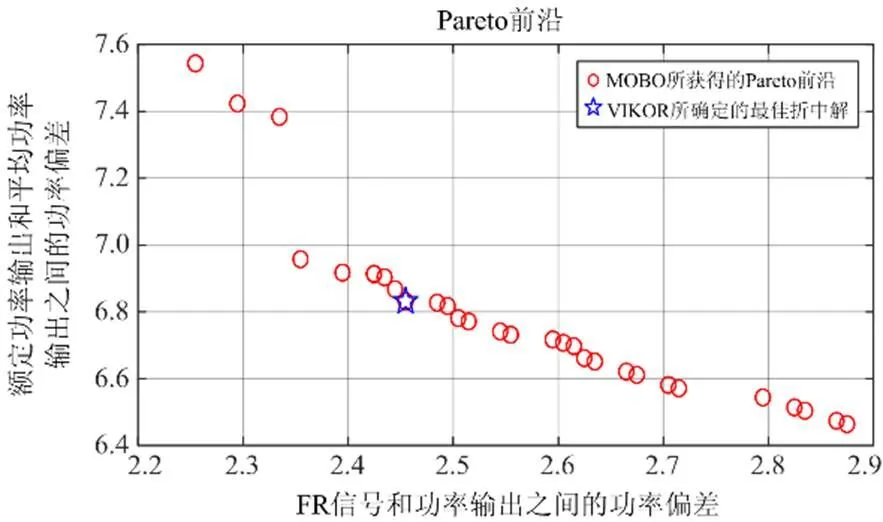
图10 时变FR信号下，MOBO所获得的最佳Pareto前沿和VIKOR所确定的最佳折衷解

图11(a)给出了时变FR信号下系统的功率输出结果。与无优化情况的功率输出相比，本文所提方法获得的功率输出更接近时变FR信号，特别是在0 min≤<5 min和10 min≤<15 min时间段内。

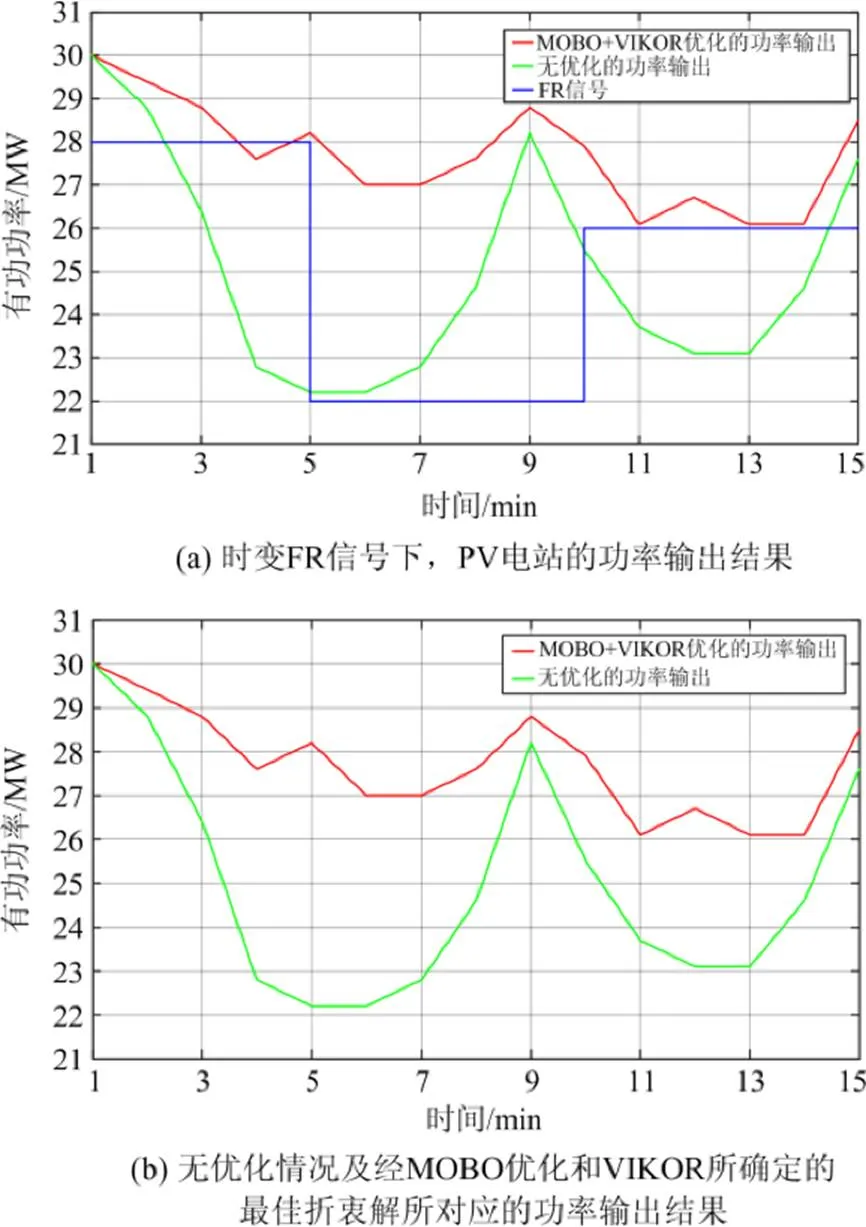
图11 时变FR信号下，基于所提方法的最佳功率输出及无优化情况下的功率输出

图12给出了时变FR信号下，所提方法与无优化情况之间的功率输出结果比较。该结果表明，与无优化情况相比，所提方法可以显著减小两个目标函数的功率偏差。通过本文所提方法获得的功率偏差分别仅为无优化情况下的51.10%和64.45%。

通过MOBO重构后的PV阵列如图13所示。比较图5和图13之间的阴影可知，MOBO可以通过将集中式阴影分散到不同的行来提高PV阵列的输出功率。

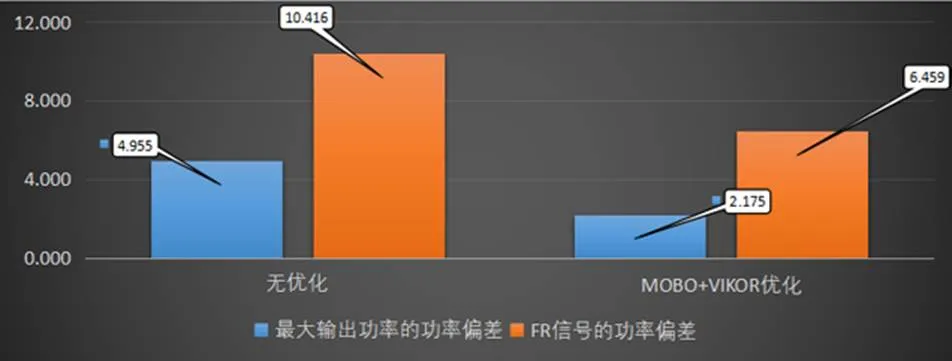
图12 时变FR信号下，所提方法与无优化情况之间的结果比较

Fig. 12 Result comparison between proposed method and that without optimization on the varying FR signals

图13 变化调频信号下，基于MOBO重构后的PV阵列最优解

4 结论

本文提出了一种新型的PV电站最优阵列重构参与电网调频的方法，致力于提升整个区域电网的动态响应性能。其主要贡献可归纳如下：

(1) 所构建的OAR不仅可以在各种阴影条件下进行PV阵列重构以实现光伏电站的最大功率输出，还进一步考虑了频率信号的影响，可以显著提高PV电站运行的经济性和所连接的电网运行的安全性。

(2) 所提MOBO可以有效地为OAR找到高质量的Pareto前沿，因此光伏电站的调度员可以根据实际需求选择高质量的最优调度方案，以满足实际运行的需要。

(3) VIKOR的设计可以从所获得的Pareto前沿中客观地确定最佳折衷解，可同时提高PV电站运行的经济性和安全性。

未来的研究将考虑把本文所提方法应用到小型光伏电站的微控制器中，以测试其硬件实施的可行性。

[1] 孙立明, 杨博. 蓄电池/超导混合储能系统非线性鲁棒分数阶控制[J]. 电力系统保护与控制, 2020, 48(22): 76-83.

SUN Liming, YANG Bo. Nonlinear robust fractional-order control of battery/SMES hybrid energy storage systems[J]. Power System Protection and Control, 2020, 48(22): 76-83.

[2] 李欣悦, 李凤婷, 尹纯亚, 等. 直流双极闭锁故障下送端系统暂态过电压计算方法[J]. 电力系统保护与控制, 2021, 49(1): 1-8.

LI Xinyue, LI Fengting, YIN Chunya, et al. Transient overvoltage calculation method of HVDC sending-end system under DC bipolar blocking[J]. Power System Protection and Control, 2020, 49(1): 1-8.

[3] 张伟晨, 熊永新, 李程昊, 等. 基于改进VDCOL的多馈入直流系统连续换相失败抑制及协调恢复[J]. 电力系统保护与控制, 2020, 48(13): 63-72.

ZHANG Weichen, XIONG Yongxin, LI Chenghao, et al. Continuous commutation failure suppression and coordinated recovery of multi-infeed DC system based on improved VDCOL[J]. Power System Protection and Control, 2020, 48(13): 63-72.

[4] 陈磊, 何慧雯, 王磊, 等. 基于限流器与断路器协调的混合直流输电系统故障隔离方法[J]. 电力系统保护与控制, 2020, 48(19): 119-127.

CHEN Lei, HE Huiwen, WANG Lei, et al. Fault isolation method of a hybrid HVDC system based on the coordination of a fault current limiter and a DC circuit breaker[J]. Power System Protection and Control, 2020, 48(19): 119-127.

[5] 赵帅旗, 肖辉, 刘忠兵, 等. 基于CSA-IP&O的局部遮阴下光伏最大功率点追踪[J]. 电力系统保护与控制, 2020, 48(5): 26-32.

ZHAO Shuaiqi, XIAO Hui, LIU Zhongbing, et al. Photovoltaic maximum power point tracking under partial shading based on CSA-IP&O[J]. Power System Protection and Control, 2020, 48(5): 26-32.

[6] SHANG L Q, ZHU W W, LI P W, et al. Maximum power point tracking of PV system under partial shading conditions through flower pollination algorithm[J]. Protection and Control of Modern Power Systems, 2018, 3(4): 400-406.

[7] FATHY A. Butterfly optimization algorithm based methodology for enhancing the shaded photovoltaic array extracted power via reconfiguration process[J]. Energy Conversion and Management, 2020, 220.

[8] 卢泉, 韦雪菲, 张玉, 等. 局部阴影情况下不同结构光伏阵列输出特性研究[J]. 太阳能学报, 2019, 40(4): 1003-1010.

LU Quan, WEI Xuefei, ZHANG Yu, et al. Research on output characteristics of photovoltaic arrays with different structures under partial shading[J]. Acta Energiae Solaris Sinica, 2019, 40(4): 1003-1010.

[9] VENKATESWARI R, RAJASEKAR N. Power enhancement of PV system via physical array reconfiguration based Lo Shu technique[J]. Energy Conversion and Management, 2020, 215.

[10] SATPATHY P R, SHARMA R. Power and mismatch losses mitigation by a fixed electrical reconfiguration technique for partially shaded photovoltaic arrays[J]. Energy Conversion and Management, 2019, 192: 52-70.

[11] MADHANMOHAN V P, SALEEM A, NANDAKUMAR M. An algorithm for enhanced performance of photovoltaic array under partial shading condition[J]. IEEE Access, 2020, 8: 176947-176959.

[12] HOROUFIANY M, GHANDEHARI R. Optimization of the Sudoku based reconfiguration technique for PV arrays power enhancement under mutual shading conditions[J]. Solar Energy, 2018, 159: 1037-1046.

[13] RANI B I, ILANGO G S, NAGAMANI C. Enhanced power generation from PV array under partial shading conditions by shade dispersion using Su Do Ku configuration[J]. IEEE Transactions on Sustainable Energy, 2013, 4: 594-601.

[14] YADAV A S, PACHAURI R K, CHAUHAN Y K, et al. Performance enhancement of partially shaded PV array using novel shade dispersion effect on magic-square puzzle configuration[J]. Solar Energy, 2017, 144: 780-797.

[15] SAHU H S, NAYAK S K. Extraction of maximum power from a PV array under nonuniform irradiation conditions[J]. IEEE Transactions on Electron Devices, 2016, 63(12): 4825-4831.

[16] NASIRUDDIN I, KHATOON S, JALIL M F, et al. Shade diffusion of partial shaded PV array by using odd-even structure[J]. Solar Energy, 2019, 181: 519-529.

[17] 海涛, 闻科伟, 胡翔, 等. 基于RBF神经网络的光伏动态重组系统[J]. 电源技术, 2017, 41(11): 1571-1574.

HAI Tao, WEN Kewei, HU Xiang, et al. Reconfiguration approach based on RBF neural network for PV arrays system[J]. Chinese Journal of Power Sources, 2017, 41(11): 1571-1574.

[18] BABU T S, RAM J P, DRAGIČEVIĆ T, et al. Particle swarm optimization based solar PV array reconfiguration of the maximum power extraction under partial shading conditions[J]. IEEE Transactions on Sustainable Energy, 2018, 9(1): 74-85.

[19] FATHY A. Recent meta-heuristic grasshopper optimization algorithm for optimal reconfiguration of partially shaded PV array[J]. Solar Energy, 2018, 171: 638-651.

[20] YOUSRI D, BABU T S, BALASUBRAMANIAN K, et al. Multi-objective grey wolf optimizer for optimal design of switching matrix for shaded PV array dynamic reconfiguration[J]. IEEE Access, 2020, 8: 159931-159946.

[21] RAJAN N A, SHRIKANT K D, DHANALAKSHMI B, et al. Solar PV array reconfiguration using the concept of standard deviation and genetic algorithm[J]. Energy Procedia, 2017, 117: 1062-1069.

[22] YOUSRI D, BABU T S, BESHR E, et al. A robust strategy based on marine predators algorithm for large scale photovoltaic array reconfiguration to mitigate the partial shading effect on the performance of PV system[J]. IEEE Access, 2020, 8: 112407-112426.

[23] BABU T S, YOUSRI D, BALASUBRAMANIAN K. Photovoltaic array reconfiguration system for maximizing the harvested power using population-based algorithms[J]. IEEE Access, 2020, 8: 2169-3536.

[24] XI L, CHEN J, HUANG Y, et al. Smart generation control based on multi-agent reinforcement learning with the idea of the time tunnel[J]. Energy, 2018, 153: 977-987.

[25] 乌云娜, 胡勇. 基于模糊多准则妥协解排序法的光伏发电投资计划优选框架[J]. 电力建设, 2016, 37(2): 50-56.

WU Yunna, HU Yong. Selection framework of photovoltaic power generation project investment plans based on fuzzy VIKOR method[J]. Electric Power Construction, 2016, 37(2): 50-56.

[26] 范瑞祥, 尹国明, 苗洁蓉, 等. 基于参数辨识的光伏组件快速MPPT方法[J]. 太阳能学报, 2020, 41(2): 296-302.

FAN Ruixiang, YIN Guoming, MIAO Jierong, et al. A quick MPPT method of PV panel based on parameter identification[J]. Acta Energiae Solaris Sinica, 2020, 41(2): 296-302.

[27] DAS A K, NIKUM A K, KRISHNAN S V, et al. Multi-objective bonobo optimizer (MOBO): an intelligent heuristic for multi-criteria optimization[J]. Knowledge and Information Systems, 2020, 62: 4407-4444.

[28] ZHANG X S, LI C Z, LI Z L, et al. Optimal mileage-based PV array reconfiguration using swarm reinforcement learning[J]. Energy Conversion and Management, 2021, 225.

Optimal PV array reconfiguration-based power grid frequency regulation strategy

HE Tingyi1, LI Shengnan1, CHEN Yiping2, WU Shuijun3, MU Runzhi3, HE Xin1, YANG Bo4, CAO Pulin4

(1. Yunnan Power Grid Co., Ltd. Electric Power Research Institute, Kunming 650200, China; 2.China Southern Power Dispatching and Control Center, Guangzhou 510663, China;3. Yunnan Electric Power Test & Research Institute (Group) Co., Ltd., Kunming 650051, China;4. Faculty of Electric Power Engineering, Kunming University of Science and Technology, Kunming 650500, China)

A mathematical model of optimal array reconfiguration (OAR) is proposed for maximizing the power output and minimizing the power deviation between the power output and the frequency regulation (FR) signal of a photovoltaic power plant. The multi-objective bonobo optimizer (MOBO) is designed to rapidly obtain an optimal Pareto front because of its high optimization efficiency. The decision-making method called VIseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR) is employed to determine the best compromise solution from the obtained Pareto front. To verify the effectiveness of the proposed multi-objective optimization, two case studies with constant and varying FR signal are carried out on a 10×10 Total-Cross-Tied (TCT) PV array under partial shading conditions (PSC). The simulation results show that the proposed method can significantly reduce the power deviation of the two objective functions compared to that without optimization. Both power deviations obtained by the proposed method under varying FR signal are only 51.10% and 64.45% of that without optimization.

optimal array reconfiguration; PV power plant; power grid frequency regulation; multi-objective bonobo optimizer

10.19783/j.cnki.pspc.210350

国家自然科学基金项目资助(61963020)；云南省基础研究计划项目资助(202001AT070096)

This work is supported by the National Natural Science Foundation of China (No. 61963020).

2021-04-01；

2021-05-26

何廷一(1987—)，男，硕士，工程师，主要研究方向为电力系统分析、机网协调；E-mail: 584786940@qq.com

杨 博(1988—)，男，博士，教授，主要研究方向为新能源发电、储能系统优化与控制以及人工智能在智能电网中的应用；Email: yangbo_ac@outlook.com

曹璞璘(1986—)，男，通信作者，博士，副教授，主要研究方向为电力系统继电保护。E-mail: pulincao@kust.edu.cn

(编辑 张爱琴)