核电站备件库存金额预测方法
邓孝林,谢宏志
(中广核核电运营有限公司 备件中心,广东 深圳 518124)
0 引言
备品备件的保障对核电站的安全稳定运行具有重要意义,然而过高的备件库存会增加电厂的运营成本,因此,需要对备件库存进行管控,在保障供应和控制库存之间寻求一个合理的平衡点。不同核电站的备件库存结构有差异性,其所存在的库存问题也不尽相同,新运营机组处于库存建立阶段,其库存呈现上升趋势,成熟机组处于库存稳态阶段。通过对核电站的库存进行预测,梳理出核电站未来的入库金额、领用金额、库存金额,备件管理人员可以基于此开展相关库存优化工作,实现核电站备件库存的精细化管理。
目前,供应链管理领域已有相对成熟的库存预测方法,主要包括回归分析预测法、时间序列分析法、灰色预测法、马尔科夫预测法、神经网络预测法等。然而核电站大部分备件的领用记录较少,对于任意一个备件而言,其对应的现场安装数量有限,与生产销售型企业库存所面临的庞大目标客户群相比较差异性较大,核电备件的需求量具有较大的不确定性。此外,很多核电备件都属于定制产品,供应商需要接到订单后才进行生产,部分备件的采购周期超过12个月,远超过常规商品,因此,不能使用生产销售型企业通用的库存预测方法对核电备件库存金额进行有效预测。基于此,本文设计了一种对入库金额和领用金额进行预测的方法,通过入库金额和领用金额对库存金额进行预测,并选用某核电站的数据进行仿真验证,当预测时长为12个月时,入库金额预测的平均相对误差为7.77%,领用金额预测的平均相对误差为7.83%,库存金额预测的平均相对误差为3.59%。
1 库存金额计算方法
各核电站的库存金额都是一个动态变化的数据,当核电站的入库库存金额大于消耗库存金额,库存金额呈现上升趋势;当电站的入库库存金额小于消耗库存金额,库存金额呈现下降趋势。库存金额的计算公式见式(1),其中S为+1时间的库存金额,S为时间的库存金额,R为时间的入库金额,L为时间的领用金额。

入库金额可以进一步细分为PO入库金额(已与供应商签署采购合同)、已审批PR入库金额(已审批采购申请,尚未与供应商签署采购合同)、新审批PR入库金额(尚新审批的采购申请)、工程期间剩余备件入库金额。入库金额的计算公式见式(2),其中1为时间的PO入库金额,2为时间的已审批PR入库金额,3为时间的新审批PR入库金额,4为时间的工程期间剩余备件入库金额。

领用金额可以进一步细分为大修领用金额和日常维修领用金额。领用金额的计算公式见式(3),其中1为时间的大修领用金额,2为时间的日常维修领用金额。

2 入库金额计算方法
入库金额是由PO入库金额、已审批PR入库金额、新审批PR入库金额、工程期间剩余备件入库金额组成,其中工程期间剩余备件入库金额只是在核电站运营前期出现,一般情况下,通过合理规划可以有效预测工程入库金额,本节重点介绍其余三种入库金额的计算方法。
2.1 PO入库金额
鉴于当前核电备件供应链管理的现状,供应商没有全部实现按照采购订单中的计划交货时间进行入库,即在任何时间都可以将PO订单分为两部分,第一部分是计划在当前时间之前入库,但实际尚未入库的订单;第二部分是计划在当前时间之后入库,实际尚未入库的订单。针对这两部分的订单,都需要通过计算其在历史上的订单入库金额分布情况,从而对未来的入库金额进行预测。


通过提取核电站历史PO入库金额以及对应采购订单的计划入库日期,可以计算出式(6)的参数矩阵,为了减少核电站某些时间出现大量PO入库或者少量PO入库对参数矩阵的影响,提升预测精度,可以通过综合过去个月的入库金额数据,计算参数矩阵,其中距离当前时间越近的权重越大。令需计算的参数矩阵为,-1时间已计算的参数矩阵为,-m时间已计算的参数矩阵为K,权重系数为,其取值范围为0~1之间,由此可以计算出参数矩阵,见式(7)。

2.2 已审批PR入库金额
已审批PR入库金额与PO入库金额的计算方法相似,均是通过统计电厂历史入库情况,计算出计划在某时间入库的采购订单实际入库时间的概率分布。首先计算当前已审批PR金额,将其赋值为2,通过统计电厂历史入库情况,可以计算出计划在某时间入库的采购订单实际入库时间的概率分布。针对未来个月的预测入库金额,可以建立一个1的矩阵,即[,...,p],其中是指已审批PR订单中在1时间的入库金额占比,p是指已审批PR订单中在时间的入库金额占比,通过式(8)可以计算已审批PR入库金额。为了提升预测精度,参考2.1章节的方法,可以通过综合过去个月的入库金额数据,计算已审批PR入库金额的参数矩阵,其中距离当前时间越近的权重越大。

2.3 新审批PR入库金额
新审批PR入库金额与已审批PR入库金额的计算方法相似,计算未来每个月预计新审批PR金额,可选用过去个月审批PR金额的平均值,将其赋值为3。在1时间的新审批PR金额为3,则其预测入库金额为3[,...,p];在2时间的新审批PR金额仍为3,由于2在1时间之后,故2时间新审批PR金额的预测入库金额为3[0,...,p];同理可计算时间新审批PR金额的预测入库金额为3[00]。将参数矩阵展开为的矩阵,对角线的值为,通过式(9)可以计算新审批PR的预计入库金额。

3 领用金额计算方法
3.1 大修领用金额
对某核电站的大修备件领用金额进行预测,需要先梳理未来的大修分布,对每一个大修的领用总金额进行预测,并将预测的金额分配到每个月。核电站的大修可以分为年度大修、十年大修和首轮大修,由于十年大修的样本较小,本文重点分析年度大修和首轮大修的预测方法。经梳理某成熟机组的年度大修金额与大修天数的分布,进行线性拟合,并对同类型机组的年度大修金额进行预测。由于新机组首轮大修金额与大修天数的相关性不明显,故将历史首轮大修金额的平均值作为未来首轮大修金额的预测值。以某核电站的13个大修为例,如图1所示,预测的大修金额与实际大修金额的平均相对误差为9.5%。

图1 大修金额与天数的关系以及预测值与实际值对比图
确立了大修金额的计算方法,需要进一步分析大修领用金额在时间维度上的分布。经梳理某核电站10个大修备件领用金额占比分布,如图2所示,绝大部分大修备件都是在大修开工前15d至大修开工后30d之间进行领用,其领用金额占比约为93.9%。
图2是按照天进行分布计算,若要按照月进行预测,则需要将大修领用金额分布分解到大修开始前一个月、大修开始的月份、大修开始后一个月。基于大修开工的具体日期,结合图2中的大修领用金额分布情况,可以计算出大修开工日期前后月份领用金额占比分布,如图3所示,若某个大修的开工日期为15号,则在开工日期前一个月的领用金额占比为6.3%,在开工日期所在月的领用金额占比为76.6%,在开工日期后一个月的领用金额占比为17.1%。
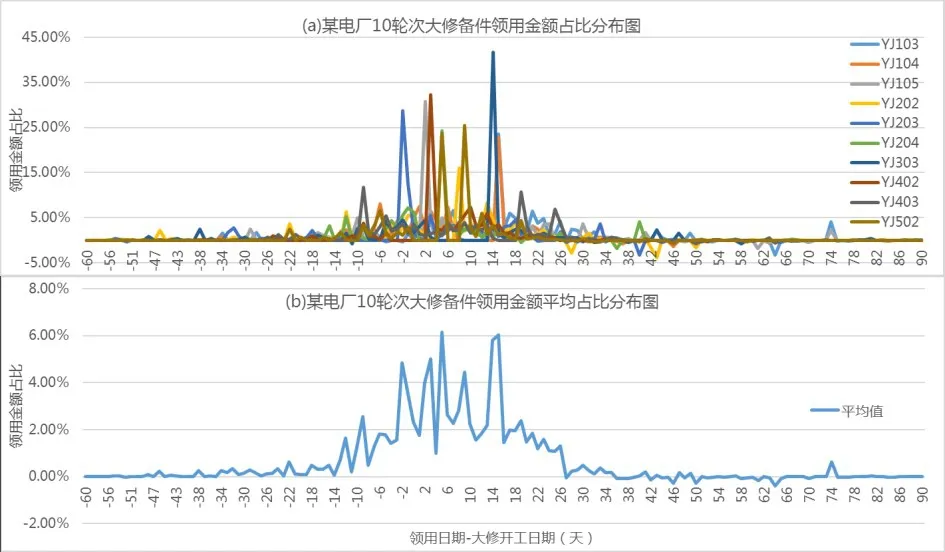
图2 大修备件领用金额分布图

图3 大修开工日期前后月份领用金额占比分布图
3.2 日常维修领用金额
日常维修领用金额通常选取过去某段时间的平均值,例如某核电站某年单堆日常维修领用金额等于过去三年单堆日常维修领用金额的均值。如图4所示,某核电站的日常维修预测领用金额与实际领用金额的平均相对误差为25.5%。若要预测某核电站每个月的日常维修领用金额,只需要使用预测的年度单堆日常维修领用金额预测值乘以核电站的堆数后再除以12。

图4 年度单堆日常维修领用金额预测图
4 仿真试验
基于本文中入库金额的计算方法和领用金额的计算方法,对某核电站的入库金额、领用金额、库存金额进行预测,并与真实值进行对比分析。
4.1 入库金额预测
基于2.1节、2.2节、2.3节的计算方法,对某核电站的PO入库金额、已审批PR入库金额、新审批PR入库金额进行预测。在某时间对未来24个月的入库金额预测结果如图5所示。从图5可以看出,随着预测时间的增加,PO入库金额的占比逐步下降,新审批PR入库金额的占比逐步上升。在预测的前6个月中,PO入库金额占了较大的比例,在预测的后12个月中,新审批PR入库金额占了较大的比例。

图5 未来24个月的入库金额预测图
为进一步评估入库金额的预测效果,对未来1个月、未来3个月、未来6个月、未来12个月的交货金额进行了滚动预测,如图6所示。由于每个月的入库金额具有一定的随机性,在对未来1个月的入库金额进行预测时,平均相对误差为37.9%。随着预测时长的增加,可以在一定程度上抵消入库金额的波动性,当预测时长为3个月时,平均相对误差为21.1%;当预测时长为6个月时,平均相对误差为6.7%;当预测时长为12个月时,新审批PR入库金额的权重增加,而未来新审批PR的金额具有一定的随机性,故总体平均相对误差为7.7%,较6个月的预测误差有所增加。

图6 不同预测区间的入库金额预测图
4.2 领用金额预测
基于3.1节、3.2节的计算方法,对某核电站的大修领用金额、日常维修入库金额进行预测。在某时间对未来24个月的领用金额预测结果如图7所示。在存在多个大修重叠的情况下,部分月份的预测领用金额会处于高位。

图7 未来24个月的领用金额预测图
为进一步评估入库金额的预测效果,对未来1个月、未来3个月、未来6个月、未来12个月的领用金额进行了滚动预测,如图8所示。由于存在部分大修备件领用后未安装在现场,大修结束后将已领出来的备件退回仓库,由此导致某些月份的实际领用金额统计值较低,甚至出现领用金额为负值的情况。为了避免因为实际领用金额为负值,导致相对误差数值失真,故在计算平均相对误差时已剔除领用金额为负值的月份。在对未来1个月的领用金额进行预测时,平均相对误差为24.6%。随着预测时长的增加,可以在一定程度上抵消入库金额的波动性,当预测时长为3个月时,平均相对误差为20.6%;当预测时长为6个月时,平均相对误差为13.0%;当预测时长为12个月时,平均相对误差为7.8%。

图8 不同预测区间的领用金额预测图
4.3 库存金额预测
基于4.1节和4.2节的预测数据,对未来1个月、未来3个月、未来6个月、未来12个月的库存金额进行了滚动预测,如图9所示。不同预测区间的入库金额、领用金额、库存金额的相对误差分布如图10所示。针对库存金额预测,在对未来1个月的库存金额进行预测时,平均相对误差为1.77%;当预测时长为3个月时,平均相对误差为3.25%;当预测时长为6个月时,平均相对误差为3.31%;当预测时长为12个月时,平均相对误差为3.59%。随着预测时长的增加,各种不确定因素也会增加,故库存金额预测的准确度会逐渐降低。
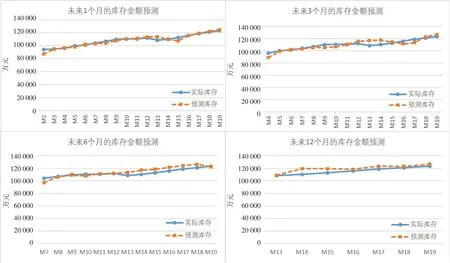
图9 不同预测区间的库存金额预测图
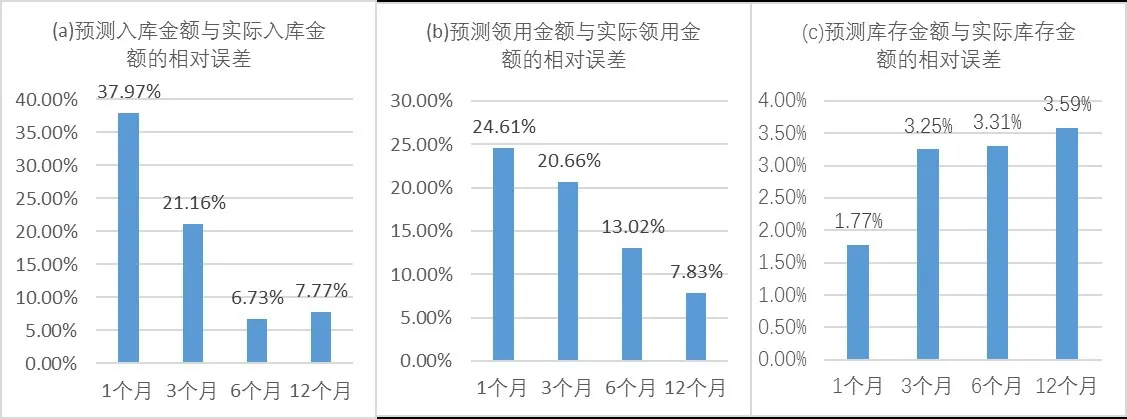
图10 入库金额、领用金额与库存金额相对误差分布图
5 结语
核电站备件入库金额和领用金额决定了库存金额的变化趋势,本文提出了一种对核电站备件入库金额和领用金额的预测方法,并基于此对备件库存金额进行预测,当预测时长为1个月时,库存金额的平均相对误差为1.77%;当预测时长为12个月时,库存金额的平均相对误差为3.59%,基本能够满足核电备件管理中对库存金额预测精度的要求。
若要提升库存金额预测的准确度,需提升入库金额和领用金额预测的准确度。针对入库金额的预测,由于不同供应商的按期交货的分布不同,可以将未来待交货的采购订单按照供应商维度展开,分别计算每个供应商的按期交货分布,由此提升整体入库金额预测的准确度。针对领用金额的预测,可以将领用金额细分为大修计划性维修、大修非计划性维修、日常计划性维修、日常非计划性维修四个部分,其中计划性维修可以通过维修大纲梳理对应备件的需求,计算备件的领用金额,非计划性维修参照历史同期领用数据,计算备件的领用金额,由此提升领用金额预测的准确度。

