Observation of the BEC-BCS crossover in a degenerate Fermi gas of lithium atoms

Xiang-Chuan Yan(严祥传) Da-Li Sun(孙大立) Lu Wang(王璐)Jing Min(闵靖) Shi-Guo Peng(彭世国) and Kai-Jun Jiang(江开军)

1State Key Laboratory of Magnetic Resonance and Atomic and Molecular Physics,Wuhan Institute of Physics and Mathematics,Innovation Academy for Precision Measurement Science and Technology,Chinese Academy of Sciences,Wuhan 430071,China 2Center for Cold Atom Physics,Chinese Academy of Sciences,Wuhan 430071,China

3University of Chinese Academy of Sciences,Beijing 100049,China

Keywords: BEC-BCS crossover,three-body recombination,anisotropic expansion

Due to the unique properties of ultracold Fermi gases,great achievements have been made in both experimental[1-4]and theoretical works[5,6]over the past decades. Such systems offer a unique platform to investigate diverse exotic physical behaviors,including thermodynamic features,[3,7,8]condensed pairs,[9,10]collective excitations[11,12]quantum simulations in optical lattice,[13]and properties of superfluidity,[14]etc. In all these investigations, the Feshbach resonance[15]provides the essential tool to control the interaction between atoms,which offers a valid technical support for studying the strongly correlated Fermi gases, and has been the key to many breakthroughs.

With the help of Feshbach resonance technology, people can modulate the interaction between atoms easily by tuning magnetic field, which specifically means that the Fermi gases can be studied between non-interacting and strongly interacting regimes. In the past decades, among the numerous explorations using Feshbach resonance,the researches on quantum behaviors in Bose-Einstein-condensation-Bardeen-Cooper-Schrieffer (BEC-BCS) crossover[16-18]are particularly attractive. The atomic system exhibits distinct properties for the two limits (BCS and BEC) beside the Feshbach resonance, while evolves smoothly in the crossover region. Specially,the most striking research is focused on the unitary limit of the inter-particle interaction,where the scattering length is infinitely big. In this unitary region,special symmetry[19]and universal characteristics[20]will emerge in the atomic system.

In this work,we experimentally observe characteristic behaviors of degenerate Fermi gases in the BEC-BCS crossover.Firstly,the magnetic field is calibrated by measuring the Zeeman shift of the optical transition. The inter-atomic interaction between the two spin components of6Li atoms is varied by tuning the magnetic field across the Feshbach resonance. Then, we measure the free expansion of Fermi gases in different interacting regimes, and find that the aspect ratio of the atom cloud shows a non-monotonic behavior across the Feshbach resonance. The density distribution is probed in different interacting regimes,where a condensate of diatomic molecules forms in the BEC limit with the indication of a bimodal distribution.We further measure the three-body recombination atom loss[21]in the BEC-BCS crossover,and find that the magnetic field of the maximum atom loss is in the BEC limit and gets closer to the Feshbach resonance when decreasing the atom temperature. This result agrees with previous experiments[22-25]and theoretical prediction.[26]

The experimental setup is briefly shown in Fig.1(a). The Feshbach magnetic field is produced by a pair of Helmholtz coils composed of hollow copper tube which is cooled by the flowing water inside. Each coil has only 30 turns and can hold up to a current of 500 A. The magneto-optical trap (MOT)coils stay inside the Feshbach coils and are composed of copper wire. The cold atoms are trapped by two 1064 nm laser beams which intersect in the center of the chamber at a small angle of 11.3°. Figure 1(b) indicates the high-field imaging system.A circularly polarized imaging beam propagates along the-zdirection,parallel to the axis of the Feshbach coils.The absorption image is amplified by a factor of 2.6 by using two lenses with focal lengths of 75 mm and 200 mm respectively.The imaging beam is obliquely incident on the glass chamber,avoiding optical interference after its perpendicular retroreflection. A D-shaped mirror is particularly used here to only reflect the MOT beam, which spatially separates the imaging beam from that of the MOT,eliminating the background noise during the imaging process.

Figure 2 shows how to control and calibrate the magnetic field across the Feshbach resonance. The electric circuit for controlling the magnetic field is shown in Fig.2(a). Two 250-A power supplies are connected in parallel to provide enough power. The magnetic field is stabilized with the help of a current transducer connected to a PID controller whose output feeds back to the MOSFET.The stability of the magnetic field can become better than 10-4after optimizing PID parameters.An IGBT module controlled by an optical signal is introduced to realize a short switching time of the magnetic field. Two varistors(3000 V and 70 V)are connected to protect the MOSFET and IGBT from being destroyed during the shutdown process. An additional varistor of 70 V,as a dissipation module,is connected in parallel to the Feshbach coils to increase the switching speed.As shown in Fig.2(b),the switching-off time is about 100µs with the dissipation module,while it is about 3 ms without the dissipation module.

Then we can study atomic behaviors of the degenerate Fermi gas in different interacting regimes by tuning the magnetic field across the Feshbach resonance. The degenerate Fermi gases of6Li atoms is produced as in our previous work.[27]In brief,we employ the MOT,compressed MOT and gray molasses as the three sequential steps of the laser cooling. Then cold atoms are efficiently loaded into an ODT(see Fig.1(a)). The evaporative cooling process is carried out between the two spin states(|1〉and|2〉)atB=832 G.

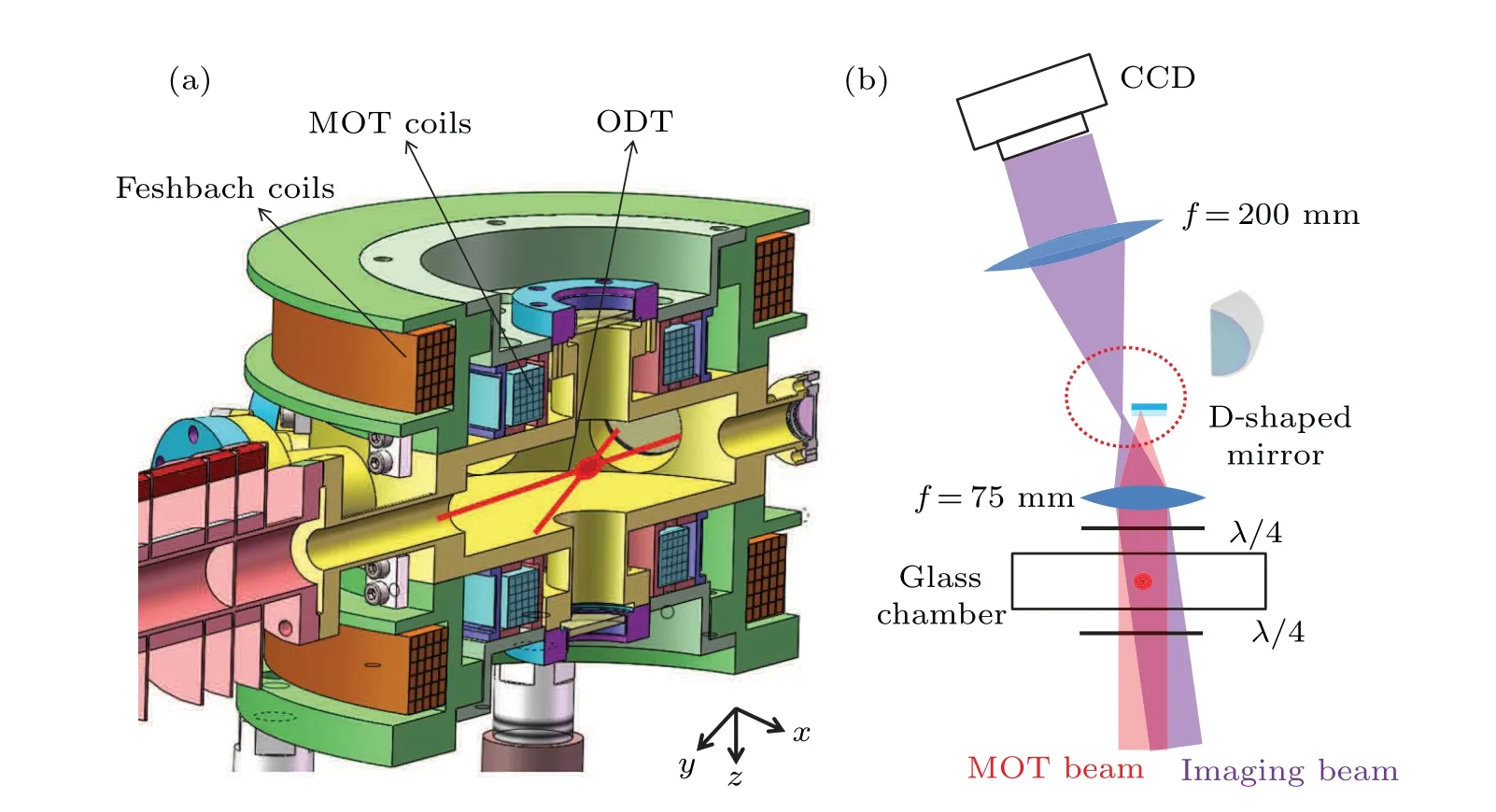
Fig. 1. Schematics of the experimental setup. (a) Configuration of the magnetic coils and optical trap. MOT: magneto-optical trap, ODT:optical dipole trap. The ODT is composed of two 1064 nm laser beams which intersect in the center of the chamber at a small angle of 11.3°.(b)The schematic diagram of the absorption imaging system. The laser beam of MOT is spatially separated from the imaging beam by using a D-shaped mirror,eliminating the background noise during the imaging process. The imaging beam is obliquely incident on the glass chamber,avoiding optical interference after its perpendicular retro-reflection.

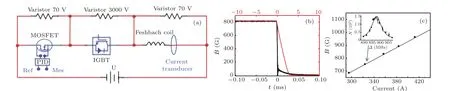
Fig.2. Manipulation and calibration of the magnetic field across the Feshbach resonance. (a)The electric circuit for controlling the magnetic field. (b)Measuring the response of the Feshbach coils when switching off the magnetic field B. With a dissipation module of Varistor 70 V(bottom horizontal axis,black line),the switching-off time is much smaller than that without the dissipation module(top horizontal axis,red line). (c)Calibration of the magnetic field B. The black dots represent the magnetic field extracted by probing the Zeeman shift of the transition2S1/2,mJ =-1/2,mI =1〉→2P3/2,mJ′ =-3/2,mI′ =1〉,and the error bar is smaller than the mark size.The black solid line is the calculation using the Feshbach coils parameters at different currents. The inset shows an example on how to measure the Zeeman shift,which is used to deduce the magnetic field B=754.1 G.-Δ is the frequency shift at B/=0 with respect to the transition frequency at B=0 G.Atom numbers N are calculated from the absorption images supposing that the one-photon detuning is kept at zero. A Gaussian function is used to fit the atom numbers,obtaining the peak position as the resonant point.

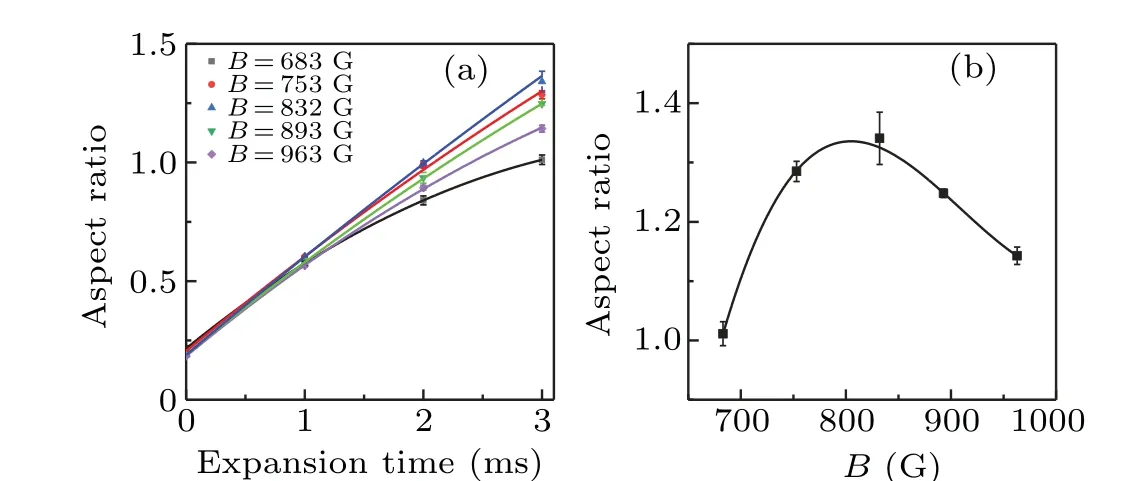
Fig. 3. Anisotropic expansion of the atomic cloud in the BEC-BCS crossover. (a) Aspect ratio vs. the time of flight at different magnetic fields B:683 G(black),753 G(red),832 G(blue),893 G(green),963 G(purple). The error bare denotes the standard deviation of 5-8 measurements. The parabolic function is used to fit the data as the eyes guide(solid curves). (b) Aspect ratios at different magnetic fields for an expansion time of 3 ms. The black solid curve is the numerical fit with a polynomial function.

To study the expansion behavior at different magnetic fields,[28]we prepare a degenerate Fermi gas atT/TF=0.5 and with an atom number of 1.3×105,whereTFis the Fermi temperature of a non-interacting Fermi gas.The atomic temperature of the unitary gas can be extracted by fitting the atomic density with a finite-temperature Fermi-Dirac distribution(polylogarithmic function).[3,27,29]In this case,the system exists as the normal gas across the Feshbach resonance. For the ODT,we measure the radial and axial trapping frequencies by probing the parametric heating and dipole mode, respectively,whereωz ≈ωx ≈2π×750.8 Hz andωy ≈2π×58.3 Hz.The residual trapping frequency of the Feshbach magnetic field is calculated to be less than 2π×3 Hz, which is negligibly small compared to that of the ODT.We change the magnetic field from 832 G to the desired value with a period of 100 ms. This small ramping rate(<1.5 G/ms)is supposed to maintain the adiabatic process.[16]To judge if the ramping is an ideal adiabatic process, it is necessary to further measure if some collective mode is excited after ramping.[30]Then the atoms are imaged after turning off the ODT and maintaining the magnetic field. The cloud sizes (σxandσy) are obtained by fitting the absorption image using a Gaussian function.The aspect ratio (σx/σy) is measured as a function of the time of flight in a magnetic field between 683 G and 963 G,as shown in Fig.3(a). The expansion rate of atomic cloud varies greatly at different magnetic fields. For comparison, Fig. 3(b) plots the aspect ratios at different magnetic fields after an expansion time of 3 ms. The aspect ratio increases when the magnetic field increases from the BEC limit to the resonance point and then decreases in the BCS limit.This non-monotonic behavior is fitted with a polynomial function(black solid curve),which gives the peak position atB0=805 G.

ENS’s group has also measured the aspect ratio of the degenerate Fermi gas atT/TF<0.2, but observe a monotonic behavior: the aspect ratio monotonically decreases when the magnetic field increase from the BEC to the BCS limit.[16]This ultracold quantum gas close to the superfluid transition has a negligible shear viscosity and can be approximately described with a theory atT=0.[31]At the finite temperature as in our work atT/TF=0.5,the shear viscosity will suppress the anisotropy of the expansion.[32,33]It has been explored that,above the superfluid transition, the shear viscosity shows a minimum close to the resonance on the BEC side,[34]which is consistent with our observation. To accurately simulate the non-monotonic anisotropic expansion, we should further develop a hydrodynamic expansion theory at finite temperature and measure the shear viscosity in the crossover.

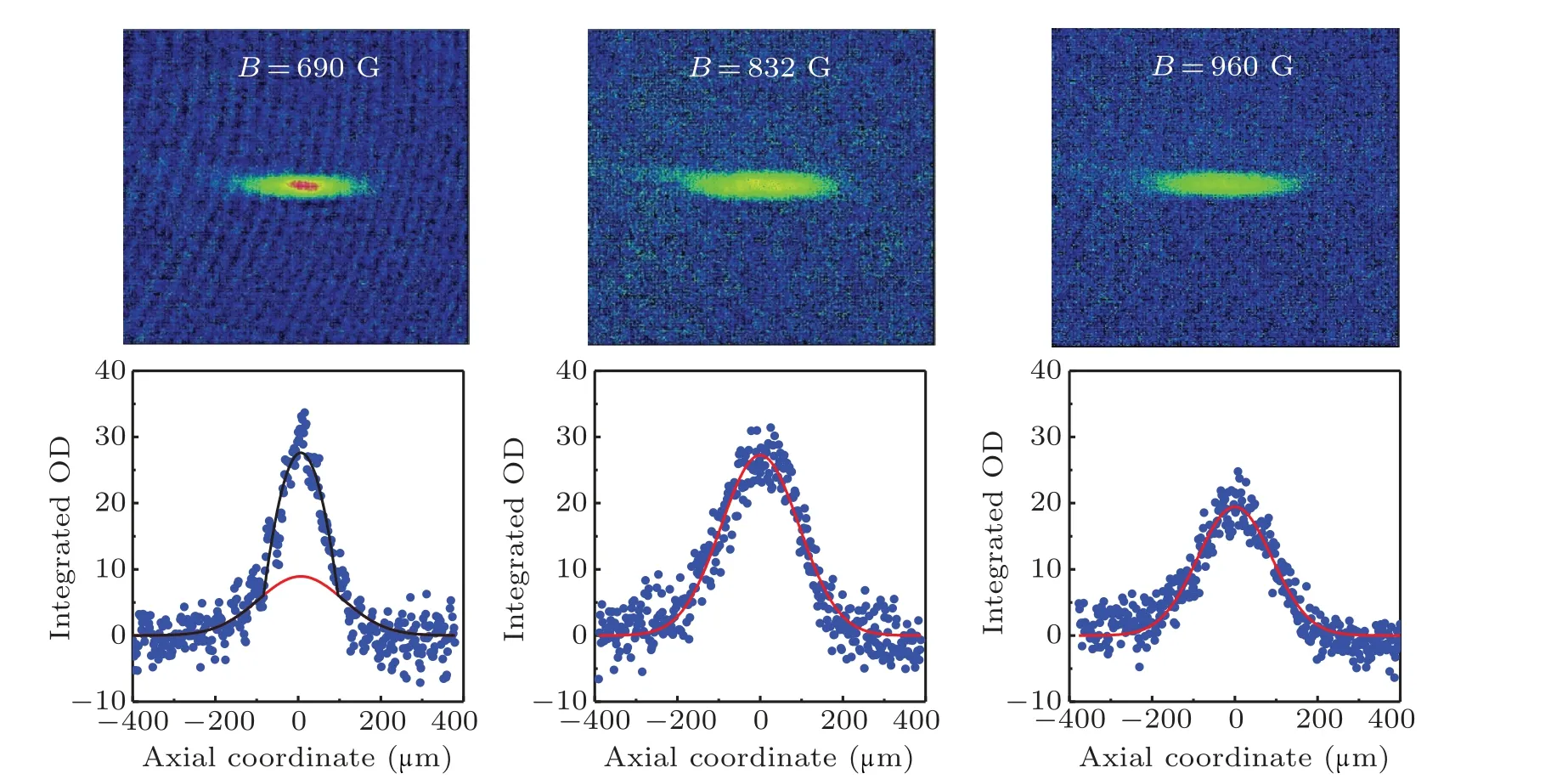
Fig.4. Density distribution in the BEC-BCS crossover. The absorption images(upper panel)and their corresponding axial integrated density profiles (lower panel) are measured in different magnetic fields across the Feshbach resonance. Left column: Bose-Einstein condensate of molecules at B =690 G. The red and black curves are fit to the Gaussian function and bimodal profile of Gaussian and Thomas-Fermi distributions,respectively. Middle column: unitary regime at B=832 G.The red curve is fit to a Gaussian function. Right column: BCS side of the Feshbach resonance at B=960 G.The red curve is fit to a Gaussian function. All images were taken with a time-of-flight of 1 ms.

The three-body recombination loss[35]is important for a strongly interacting Fermi gas,which puts a limit on the lifetime of the system and the time scale to do the experiment.In Fig. 5(a), we measure the atom loss as well as the atomic cloud size at different magnetic fields withT/TF=1.24. The holding time of atoms in the trap is 500 ms. It can be seen that the magnetic field of the maximum atom loss corresponds to that of the maximum atomic cloud size. A Gaussian function used to fit the remained atom numbersN(see the black solid curve)gives the minimum position atB*=696 G,which indicates the maximum atom loss. The three-body recombination process is affected by many factors, such as atomic interaction strength,depth of the trap and atomic temperature,etc. In order to study the effect of temperature,we measureB*at different temperaturesT/TF. Figure 5(b)showsB*versusT/TF.For comparison,the results of other experimental groups,such as MIT,[22,23]Innsbruck University[24]and ENS,[25]are also listed together. All the measurements from different groups are consistent.

It is predicted[26]that the three-body recombination loss originates from the two-step process.The first step is that three atoms recombine into a shallow dimer and an atom, and at the same time, the shallow dimer can disassociate into atoms when colliding with the atom. This process will not cause the loss because the binding energy of the shallow dimer is generally smaller than the trapping potential. The second step is that the shallow dimer will form the deep bind molecule when colliding with another shallow dimer or atom. This step will cause loss due to releasing high energy. So the number of shallow dimers formed in the first step determines the loss rate of the three-body recombination. When the scattering length increases in the BEC limit, the formation rate of the shallow dimer becomes large,but the shallow dimer disassociates into atoms rapid also due to the smaller binding energy. This is the reason that the maximum atom loss always occurs in the BEC limit below the resonance as seen in Fig.5(b). With the decrease ofT/TF,B*gradually approaches the Feshbach resonance.

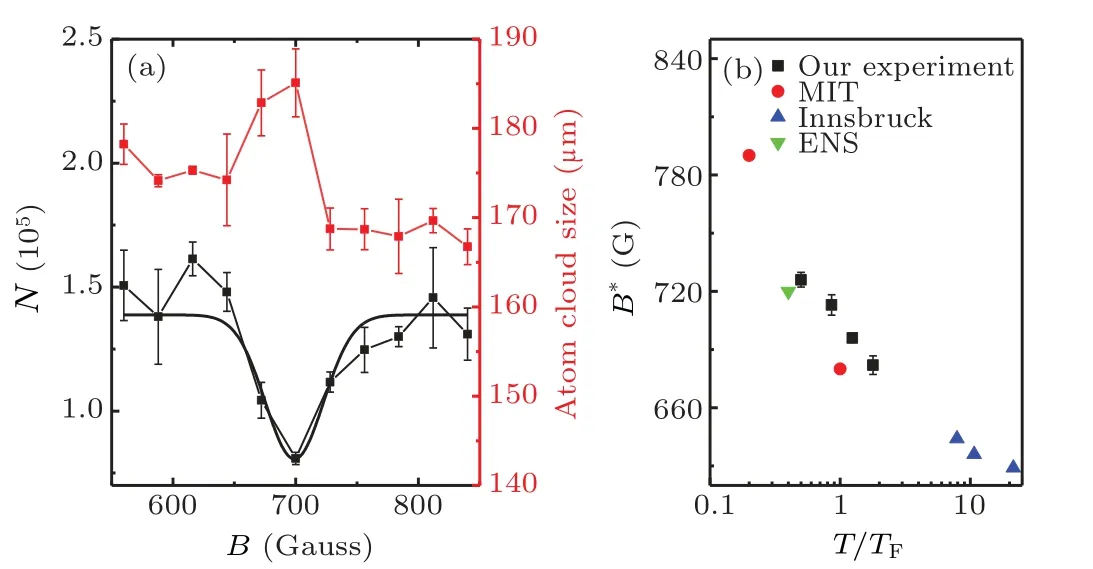
Fig. 5. Three-body recombination loss in the BEC-BCS crossover. (a)Remained atom number N as well as atom cloud size vs. the magnetic field. The error bar denotes the standard deviation of measurements.T/TF=1.24.A Gaussian function is used to fit the data(black solid curve),giving the magnetic field B* =696 G of the maximum atom loss. (b)The magnetic field B* of the maximum atom loss for different atomic temperatures. The horizontal axis is logarithmically plotted. The error bar comes from the Gaussian fitting. Experimental results from MIT,Innsbruck University and ENS are also given as a comparison.

In conclusion, we realize the BEC-BCS crossover of the degenerate Fermi gas by tuning the magnetic field across the Feshbach resonance.Some characteristic behaviors of the system have been explored in the strongly interacting regime. A non-monotonic anisotropic expansion is observed across the Feshbach resonance. A condensate of diatomic molecules forms in the BEC limit with the indication of a bimodal distribution. The magnetic field of the maximum atom loss is in the BEC limit and increase towards the Feshbach resonance when decreasing the atomic temperature. Our measurements agree with the theoretical prediction and previous experiments. This work builds up a controllable platform for the study on the strongly interacting Fermi gas.

Acknowledgements

This work has been supported by the National Key Research and Development Program of China (Grant No.2016YFA0301503), the National Natural Science Foundation of China (Grant Nos. 11674358, 11434015,and 11974384), Chinese Academy of Sciences (Grant No.YJKYYQ20170025),and K.C.Wong Education Foundation(Grant No.GJTD-2019-15)).