Protection of entanglement between two V-atoms in a multi-cavity coupling system

Wen-Jin Huang(黄文进) Mao-Fa Fang(方卯发) and Xiong Xu(许雄)

1Synergetic Innovation Center for Quantum Effects and Applications,Key Laboratory of Low-dimensional Quantum Structures and Quantum Control of Ministry of Education,School of Physics and Electronics,Hunan Normal University,Changsha 410081,China

2School of Physics and Electronics,Hunan Key Laboratory of Super Microstructure and Ultrafast Process,

State Key Laboratory of Powder Metallurgy,Central South University,Changsha 410083,China

Keywords: V-atom,multi-cavity coupling system,entanglement,negativity

1. Introduction

Quantum entanglement is an important physical resource for quantum information processing,and reflects the non-local relationship of quantum systems. Quantum entanglement has been implemented in multiple physical system experiments for performing communication and computing tasks,attracted widespread attention in the detection of quantum correlation and the quantification field, and played an important role in quantum key distribution, quantum superdense coding,[1]quantum teleportation,[2]and quantum algorithm. In general,since quantum systems will inevitably interact with the surrounding environment,[3,4]quantum entanglement attenuates,or even sudden death.[5,6]In recent years,the phenomenon of entanglement death and recovery in different systems has been studied.[7-10]Since entanglement needs to be prevented from disappearing for a period of time until the quantum task can be completed in the process of quantum information processing,how to prepare sustained and stable entangled resources in a dissipative environment is one of the most concerned problems in quantum information field.

So far, a lot of research has focused on the manipulation and protection of quantum entanglement. For example, entanglement can be protected by using the quantum Zeno effect[11,12]and the dynamically decoupled pulse trains, but from a practical point of view, these procedures are very demanding. For a two-level atomic system, a relatively simple way to protect the quantum entanglement is to place two two-level atoms in two separate dissipative cavities,and the two-level atom interacts locally with its own dissipative cavity which is coupled to an external cavity with high quality factor (ECWHQF).[13]It can also satisfy the requirement of independent control in quantum information processing. Most previous studies have focused on two-level atomic systems. As we all know, three-level atomic system has more advantages.[14-16]It provides higher capacities, more secure cryptography as well as superior quantum gates. Derkaczet al.[17]extended the entanglement dynamics from two-dimensional systems to three-dimensional systems through studying the entanglement dynamics of threelevel atomic systems. Since then, there have been more and more studies on entanglement in three-level systems.[18]So,can we find a better way to protect quantum entanglement resources in the three-level atomic system?

This paper studies the protection of entanglement between two V-atoms (EBTVA) in a multi-cavity coupling system where the two V-atoms are initially in the maximum entangled state and interacts locally with its own cavity which is coupled to ECWHQF.When there is no ECWHQF,the influence of the coupling strengthJbetween the V-atom and the cavityCl0, and detuningδon the entanglement between the two V-atoms are discussed. The results show that in the case of strong coupling and small detuning, the entanglement between two V-atoms will not evolves to zero. And in the case of weak coupling and large detuning, the system can effectively protect the EBTVA.By considering the two dissipative cavities have the same numbernof ECWHQF, the influence of the numbernof ECWHQF and the coupling strengthkon the EBTVA are discussed respectively. The results show that the protection of two V-atoms entanglement in the dissipative cavity is enhanced with the increase of values ofnandk,and better results can be obtained when the V-atom and the dissipative cavity are weakly coupled.

This paper is organized as follows.In Section 2,the physical model and the method adapted to measure entanglement are presented. Then in Section 3, by numerical calculation,an effective way for protecting the EBTVA in a multi-cavity coupling system is given. Finally, conclusions are presented in Section 4.

2. Physical model and the method adapted to measure entanglement

The system consists of two V-atoms(labeled as A and B)in a multi-cavity coupling system,where the two V-atoms are initially in the maximum entangled state and interacts locally with its own dissipative cavity(labeled asCA0andCB0)with the dissipation ratesΓA0andΓB0, and the two dissipative cavities coupled to the same numbernof ECWHQF. The model of a V-atom and the whole system are shown in Fig.1,respectively.

Fig.1. The model of a V-atom and the multi-cavity coupling system. (a)The model of a V-atom;(b)n=0(red dotted box);n=1(solid black box);n=2(dotted black box)and n=3(the whole system).

Due to the external cavities are cavities with high quality factor,the Hamiltonian of the system can be written as(¯h=1)

where‖ · ‖represents the trace norm which is defined as‖ρ ‖=tr(ρρ†)1/2. For this system,the density matrix of two V-atoms can be given byρatom=Trcavityρ. Using Eq.(6),we can obtain the EBTVA in this system.

3. Numerical results of entanglement between two V-atoms

We will discuss the effective ways for protecting the EBTVA in the multi-cavity coupling system in two cases,without and with ECWHQF,respectively.

3.1. The case without ECWHQF

In general,Eq.(1)can not be solved exactly. When there is no ECWHQF,it corresponds ton=0 andkl0=0 in Eq.(4),and the numerical results of the EBTVA are shown in Figs.2 and 3 for different parameters. Assume that the two V-atoms are initially in the maximum entangled state with the form of

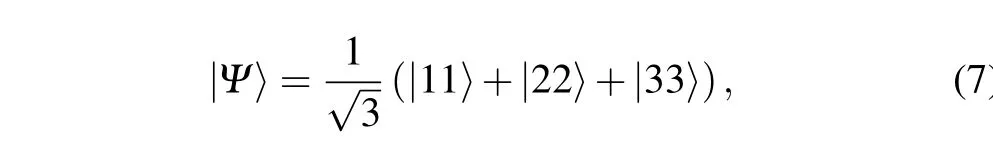
andΓA0=ΓB0=Γ. We show the influence of the coupling strength between V-atoms and dissipative cavitiesCl0and detuningδon the EBTVA in Figs.2 and 3.

Fig. 2. Influence of coupling strength J between the V-atom and the cavity Cl0 on the EBTVA:(a)weak coupling case;(b)strong coupling case.The two V-atoms are initially in the maximum entangled state with ΓA0 =ΓB0 =Γ,and δ =0.1Γ.

Figure 2 shows the influence of the coupling strengthJbetween the V-atom and the cavityCl0on the EBTVA. Figure 2(a) corresponds to the weak coupling case (J= 0.1Γ,0.15Γ, and 0.2Γ), while Fig. 2(b) describes the strong coupling case(J=0.4Γ,0.6Γ,Γ,and 2Γ). It can be clearly seen from Fig.2(a)that when the coupling between the V-atom and the cavity is weak, the EBTVA will decay to 0, and the fast or slow of decay depends on coupling strengthJ,as the value ofJincreases, the value of the EBTVA drops faster. From Fig.2(b),it is obvious that,in the strong coupling case,the system can protect partially the EBTVA.With the increases ofJ,the better the protection on the EBTVA can appear. When the coupling strength between the V-atom and the cavityCl0is 2Γ,the value of the EBTVA can be maintained at 0.32.When continue to increase the value ofJ,the protection on the EBTVA of the system will not increase significantly. Therefore,in the case of small detuning, the system can protect partially the EBTVA in the strong coupling case without ECWHQF.

Fig. 3. Influence of detuning δ on the EBTVA. The two V-atoms are initially in the maximum entangled state with ΓA0 =ΓB0 =Γ. (a)J=0.2Γ;(b)J=0.6Γ;(c)J=2Γ.

The influence of detuningδon EBTVA are shown in the contour plots in Figs.3(a)-3(c), and the other parameters are the same as those in Fig.2.Figure 3(a)shows the case of weak coupling case withJ=0.2Γ.When the value ofδis small,the decay rate of the EBTVA is relatively fast,and when the value ofδbecomes large,the decay rate of the EBTVA is slow(see Fig. 3(a)). Therefore, under the condition of weak coupling and large detuning,the EBTVA can be well protected.

Figures 3(b) and 3(c) show the case of strong coupling between V-atom and dissipative cavity withJ= 0.6ΓandJ= 2Γ, respectively. Comparing Figs. 3(b) and 3(c) with Fig.3(a),it can be found that the protection of the system on the EBTVA in strong coupling is worse than that in weak coupling case. In the case of large detuning, and the weak coupling between the V-atom and the dissipative cavity, the system has a very obvious protection on the EBTVA.Comparing the results shown in Fig.2,we found that the protection of the system on the EBTVA is better than that under the conditions of small detuning and strong coupling. These results can be explained physically: when the coupling between the V-atom and the dissipative cavity is weak,it can be interpreted as the interaction between the V-atom and the external environment has been reduced. When the value of detuning between the transition frequency of the V-atom and the cavity frequency is large, the stimulated radiation of the V-atom is limited. So the EBTVA can be protected better with weak coupling and large detuning. It is worth noting that we also find the decay of the EBTVA is fastest when the value ofδis approximately equals toJ(see black dotted line in Fig.3).Therefore,in order to have a good protection on the EBTVA for the system, the value ofδshould be avoided to be close to the value ofJ.

In the discussion above, only the case ofn=0 is mentioned. In the case of small detuning and strong coupling,the EBTVA can be protected partially in a small degree of entanglement. In the case of weak coupling with large detuning,the EBTVA can be protected in a large entanglement degree. But from the discussion above,we can see that,in the case without ECWHQF the EBTVA can not be protected perfectly and continuously. Can we find a way to make the EBTVA be better protected?

3.2. The case with ECWHQF

Consider the same number of the ECWHQF coupled with two dissipative cavities as shown in Fig. 1. In order to simplify the calculation,we consider that the coupling constantkbetween cavityCl0and ECWHQFClnare the same. The two V-atoms are initially in the maximum entangled state given by Eq. (7). When different numbersnof ECWHQF are respectively coupled outside the two cavitiesCl0,the influence of the numbernof ECWHQF and the coupling strengthkon the evolution of the EBTVA are shown in Figs.4 and 5 for different coupling strengthJbetween the V-atom and the dissipative cavityCl0.

Figures 4 and 5 show the influence of the numbernof ECWHQF and the coupling strengthkon the EBTVA in weak and strong coupling cases,respectively. Figure 4 is weak coupling case withJ=0.2, and Figs. 4(a)-4(c) are corresponding to the case ofk=0.2Γ, 0.5Γ, andΓ, respectively. From Fig. 4, we can find two cases. The first case is that, when there is no ECWHQF, the value of the EBTVA quickly decays to zero no matter what the values ofnandkare chosen(showing in dotted line in the figure). The second case is that,when there is ECWHQF, as the numbernof ECWHQF and the value ofkincreases,the protection function of the system on the EBTVA is significantly enhanced.Comparing three figures in Fig.4,whenn=3 andk=Γ,the value of the EBTVA can be maintained at about 0.95. In this case, we can realize perfectly and continuously the protection of multi-cavity coupling system on the EBTVA. Figure 5 corresponds to the case of strong coupling withJ=0.6, and it shows that only the value ofkis large,the multi-cavity coupling system has an obvious protection function on the EBTVA.Whenk=Γandn=3,the value of the EBTVA is about 0.64.

Fig.4.The influence of the number n of ECWHQF and the coupling strength k on the EBTVA in the weak coupling case with J=0.2,ΓA0 =ΓB0 =Γ and δ =0.1Γ. (a)k=0.2Γ;(b)k=0.5Γ;(c)k=Γ.

Fig.5.The influence of the number n of ECWHQF and the coupling strength k on the EBTVA in the strong coupling case with J =0.6, ΓA0 =ΓB0 =Γ,δ =0.1Γ. (a)k=0.2Γ;(b)k=0.5Γ;(c)k=Γ.

From the discussion above, it can be seen that, by considering the case with ECWHQF, the protection function of the system on the EBTVA becomes better as the values ofnandkincrease under weak coupling case. While in the case of strong coupling,only when the value ofkis larger,the system has a protection function on the EBTVA.These results can be explained physically: whenn=1 in Eq.(4),the multi-cavity coupling system can be viewed as the physical realization of a photonic band gap[19]for each V-atom, and it refers to a certain frequency range of waves cannot travel in the structure,acting as a filter,the structure filters out waves in the range of frequencies that allow the atom interacts with the field,effectively shielding the atom from the outside environment. Whenn=3 andk=Γ, the EBTVA can be perfectly and continuously protected.

Finally,we discuss the possibility of the multi-cavity coupling system in experiment. The parameters in this paper can take the following values in the real experiments:[20-28]ΓA0=ΓB0=Γ ∈[1 MHz,10 MHz],k,J ∈[0.1Γ,10Γ], andωA0=ωB0=ω0=2π×10 GHz. Taking Fig. 4(c) as an example,the time can be estimated astn=0=14/Γ ∈[1400 ns, 14 µs]andtn=1=6000/Γ ∈[0.6 ms, 6 ms]. Due to the limitations of the memory of the computer,we can not calculate the time whenn=2 andn=3, but there is no doubt that the EBTVA will last much longer. We can also surmise that the protection function will be better if we continue to increase the numbernof ECWHQF.

4. Summary and conclusion

We have studied the protection of the EBTVA in a multicavity coupling system. When there is no ECWHQF, the value of the EBTVA can be maintained at about 0.32 for the case of strong coupling and small detuning, and protected in a large entanglement degree for the case of weak coupling and large detuning. But on the whole, the EBTVA can not be protected perfectly and continuously in the case without ECWHQF,while when there is ECWHQF,the EBTVA can be significantly enhanced. In the case of weak coupling, as the values ofnandkincrease,the protection function of the system on the EBTVA can be greatly enhanced. For example,the value of the EBTVA can be maintained at about 0.95 whenk=Γandn=3. Hence, in the cases with ECWHQF and weak coupling,by selecting the appropriate parametersnandk,we can realize perfectly and continuously the protection of multi-cavity coupling system on the EBTVA. Therefore, our result provides an effective method for protecting entanglement resources of three-level system. In addition, only the case where the V-atoms are stationary in the cavities is considered in this paper, the influence of atomic motion of V-atoms on the EBTVA in this system is what we are studying and the results will be submitted elsewhere.

Acknowledgment

Project supported by the National Natural Science Foundation of China(Grant Nos.12064012 and 11374096).