Probing structural and electronic properties of divalent metal Mgn+1 and SrMgn(n=2–12)clusters and their anions

Song-Guo Xi(奚松国) Qing-Yang Li(李青阳) Yan-Fei Hu(胡燕飞) Yu-Quan Yuan(袁玉全)Ya-Ru Zhao(赵亚儒) Jun-Jie Yuan(袁俊杰) Meng-Chun Li(李孟春) and Yu-Jie Yang(杨雨杰)

1School of Physics and Electronic Engineering,Sichuan University of Science&Engineering,Zigong 643000,China

2Department of Applied Physics,Chengdu University of Technology,Chengdu 610059,China

3College of Physics&Optoelectronics Technology,Baoji University of Arts and Sciences,Baoji 721016,China

Keywords: SrMgn (n=2-12)clusters,CALYPSO code,density functional theory(DFT)optimization

1. Introduction

During the past decades, owing to the special structure and bonding properties, a great many of studies on magnesium (Mg) clusters have been conducted theoretically and experimentally.[1-7]It is worth mentioning that density functional theory(DFT)with appropriate functional and basis sets is known as an efficient method for clustering study.[8-11]Taking the research of neutral and charged Mgnclusters for example, Xiaet al.[6]studied the aromatic homonuclear Mg17cluster by using the B3PW91 functional with the 6-311+G(d)basis set,and their results displayed that the Mg17cluster is the first neutral locallyπ-aromatic homonuclear all-metal cluster.Belyaevet al.[7]reported the electronic, spectral, structural,and thermodynamic characteristics of Mgn(n=2-31) clusters at B3PW91/6-31G (d), B3PW91/6-311+G (2d) set levels, then they revealed that in the range of Mg2-Mg31, the atomization energy and band gap energy have significant nonmonotonic changes,and gradually approach to the atomization energy and band gap energy of ideal metal.

In recent years, there have been many studies on doping clusters.[12-20]Wanget al.[12]investigated AunM2(n=1-6,M=Ni,Pd,and Pt)clusters and found that the average atomic binding energies of this clusters are close to a limit, which is in a range of 1.56 eV-2.00 eV. Kuanget al.[13]discussed the DFT results of AunAg(n=1-12)clusters and discovered that all the AunAg (n=1-12) clusters prefer low spin multiplicity. For Mg cluster doping, Zhuet al.[14]employed the DFT method of SiMgn(n=1-12)clusters with B3LYP/6-311G(d)and found that SiMg5and SiMg8clusters were more stable than other clusters. Zhanget al.[15]used the DFT method of Be2Mgn(n=1-20) clusters with B3PW91/6-31G and found that Be2Mg8cluster is the most stable. To the best of our knowledge, there are few researches on strontium (Sr)-doped Mg clusters. So we hope this theoretical calculation can provide some references for subsequent studies.

Sr is a silver-white alkaline earth metal with yellow luster.Owing to its soft texture,Sr has good conductivity for heat,and it can also be used to make alloy, photocell and lighting material because of its active chemical properties. The Mg-Sr is a common binary alloy constituted by Mg and alkali earth elements,and possesses important applications in various fields,such as biodegradable metallic materials. Guet al.[21]studied the binary Mg-Sr alloy systems in the as-rolled state as biodegradable materials for skeletal applications. Bornapouret al.[22]reported that the Mg-0.5Sr alloy increases the vitality of human umbilical vein endothelial cells and showed a lower risk of thrombosis than WE43 stent. Comparing with other alkaline earth metals,the electronic properties of SrMgnclusters are still lacking in systematic analysis. Some essential questions arise as follows. (i) Of the anionic and neutral SrMgnclusters, which structure is the most stable? (ii) If Sr atoms are doped into Mgnclusters, will the clusters produce strange structures? (iii)Will delocalized bonding occur when Sr atoms are involved? To reveal these problems,article warm ptimization algorithm combined with DFT is adopted to probe the cluster structure,and the most stable structure of SrMg0/-nclusters was studied in detail. Next, the PES simulation of SrMg-nclusters is discussed. The stability, electronic properties and bonding properties of the anionic and neutral SrMgnclusters are analyzed in detail. We hope that these results in this work can provide some valuable guidelines for the subsequent theoretical and experimental researches about Sr-doped magnesium materials.

2. Computational detail

In this work,the CALYPSO code[23,24]which relies only on the chemical composition and can quickly predict the lowvalue isomers of the cluster by the particle swarm optimization algorithm is employed to acquire the most stable structure of Mg0/-nand SrMg0/-nclusters. Many researches have demonstrated that this method is effective and reliable for cluster structure prediction.[25-32]For getting the variable structures of Mg0/-nand SrMg0/-nclusters, we perform 50 generations to achieve the converged structure, including 30 structures for each generation,80%of which are generated by PSO algorithm and the remaining are generated randomly. Then 1500 structures of variable isomers can be obtained for each of Mg0/-nand SrMg0/-n.Considering that there have been seldom researches of Sr-Mg system with DFT framework, we conducte a series of tests to obtain the suitable functional method,and we also find that the B3PW91 method is the most suitable for Sr-Mg system. In order to save computing resources,the fundamental energy computations and geometric optimizations of the above-mentioned isomers are performed at the B3PW91/3-21G level. Then, the top 100 lower energy isomers are picked out as the initial configurations to re-optimize at the B3PW91/LANL2DZ level[33]for Sr and B3PW91/6-311+G(d) level[34]for Mg implemented by the Gaussian09 program package.[35]The influence of the spin multiplicity has also been fully considered.Considering the fact that the orbital components need analyzing,the GENECP-labeled basis set is a combination of 6-311+G(d)basis set[34]and SDD[36]basis set for the Mg atom and Sr atom, respectively. Furthermore,the charge transfers among Sr and Mg atoms, the analysis of the bonding features,as well as the simulated PES of anionic clusters based on the Koopman theorem[37]are studied in detail with the assistance of Multiwfn program[38]including the method of adaptive natural density partitioning(AdNDP).[39]

3. Results and discussion

3.1. Geometric structure

Figure 1 displays the most stable structures of the neutral and anionic Mgn+1and SrMgn(n=2-12) clusters. The corresponding electronic states and symmetries are listed in Table 1. For investigating the influnces of Sr atom doping on Mg clusters, we first discuss the pure Mg clusters. Notably,the most stable structures(shown in Fig.1)of Mgnclusters in our computation are consistent well with the results reported previously.[40-42]All of these show that the functional and basis sets adopted in our work for magnesium and doped magnesium clusters are reliable.

Fig.1. Global minimum structures of neutral and anionic Mgn+1 and SrMgn(n=2-12)clusters.

Table 1. Electronic states,symmetries,average binding energies Eb (in unit eV),highest occupied molecular orbital and lowest unoccupied molecular orbital(HOMO-LUMO)energy gaps Eg (in unit eV),and charges on Sr atoms of most stable SrMg0/-n (n=2-12)clusters.

3.2. Photoelectron spectra of anionic Mgn and SrMgn clusters

It is well known that the comparison between the theoretical photoelectron spectra(PES)and the experimental PES is an effective way to verify the reliability of theoretical computation for cluster.[6]Therefore,in Figs.2 and 3,we present the simulated PES for great majority Mg-nand SrMg-nclusters and the available experimental PES.The PES are simulated in an energy range of 0 eV-6 eV. Figure 2 shows that the simulated PES of our lowest energy isomers Mg-nare consistent with the experimental results,which indicates that the method employed in this work is reliable. From Fig.3,the simulated PES of SrMg-2cluster includes two sets of bimanals, which are 1.87, 2.32, and 4.24, 4.50, respectively, as well as a major spike at 0.79 eV in which the binding energy of the first peak(X)is in agreement with the vertical detachment energy(VDE) value of the SrMg-2cluster. With regard to SrMg-3cluster,some significant peaks at 0.93 eV,2.56 eV,and 5.30 eV are existent.The VDE value of SrMg-4is 1.07 eV,which is the first peak(X)shown in the simulated spectrum.Following this peak,other peaks are centered at 1.90,2.93,and 3.38 eV.In addition,the simulated PES of SrMg-5cluster display a weak first peak at 1.26 eV,six peaks concentrate in a range of 1.97 eV-4.18 eV.As for SrMg-6,after the first peak(X)at 1.43 eV,the second strong peak concentrates at 2.10 eV,the others(3th-8th peaks)are located at 2.34,3.16,3.50,4.08,4.64,and 4.86 eV.The VDE value of SrMg-7cluster is 1.70 eV,followed closely by the strong second peak at 2.40 eV.The SrMg-7has two attenuation peaks at 4.14 eV and 5.21 eV. The VDE value of SrMg-8cluster is centered at 1.84 eV, shown by the position of X, and the binding energies of the other peaks are 2.41,4.63, and 5.12 eV, respectively. The identical first peaks (X)with 1.70 eV are found in the simulated spectra of SrMg-7and SrMg-9. In addition,the other two single peaks of SrMg-9are centered at 2.72 eV and 5.31 eV. In Fig. 3, when the number of Mg atoms is more than 8, the photoelectron spectrum of SrMg-nshows more complexity. The SrMg-10cluster includes two weak peaks located at 1.60 eV(X)and 3.93 eV,and two intense peaks center at 2.89 eV and 5.56 eV.For SrMg-10cluster,the position of X represents the VDE value(2.00 eV),and SrMg-11includes the other five peaks located at 2.71,3.12,3.87,4.52,and 5.46 eV.The VDE of SrMg-12is 2.09 eV,which is shown by the position of X.The next five peaks are observed at 2.36,2.90,3.90,4.92,4.98,and 5.53 eV,respectively.

Table 2 displays the VDE values of Mg-n(n=3-13)and SrMg-n(n=2-12) clusters from the PES of Figs. 2 and 3.From Table 2, we can see that the corresponding values of VDE of SrMg-nwhenn=2-8 are smaller than those of Mg-n,

whereas whenn=9,11,12,the corresponding values of VDE of SrMg-nare larger than those of Mg-n.

What is worth mentioning is that there are few reports about the experimental PES of SrMg-nclusters. Because of this,we hope that the theoretical PES in this paper can be used to identify the structure of the SrMg-nclusters.

Fig.2. Comparison between simulated PES and the experimental results for the most stable Mg-n clusters.

Fig.3. Simulated PES of the most stable SrMg-n clusters.

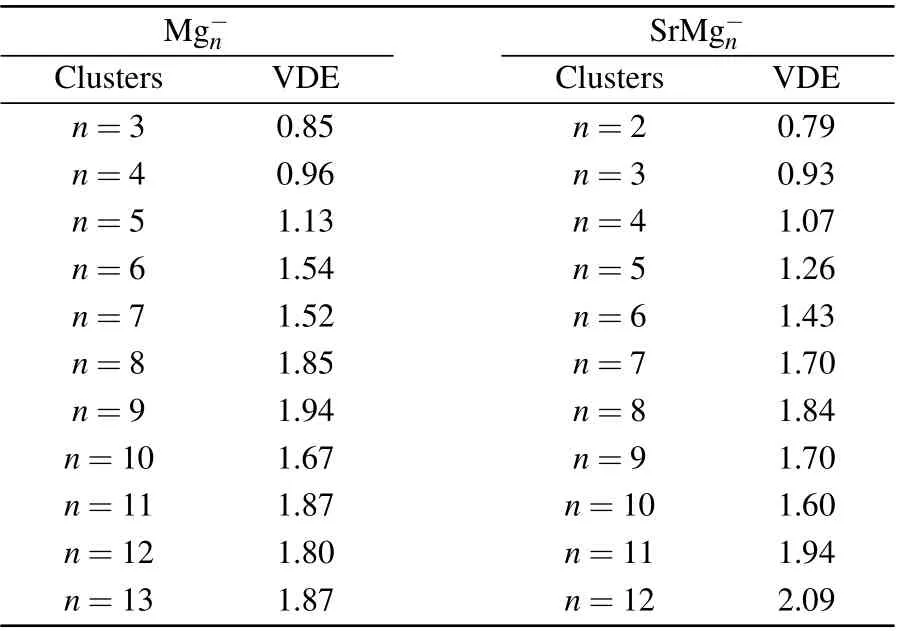
Table 2. VDE values of Mg-n (n=3-13)and SrMg-n (n=2-12)clusters(in unit eV).

3.3. Size-dependent relative stability

For the cluster science, the intrinsic stability of cluster can be expressed by the mean binding energy (Eb) and the second-order energy difference (Δ2E). For SrMg0/-n(n=2-12)clusters,theEband Δ2Ecan be expressed as the following expressions:

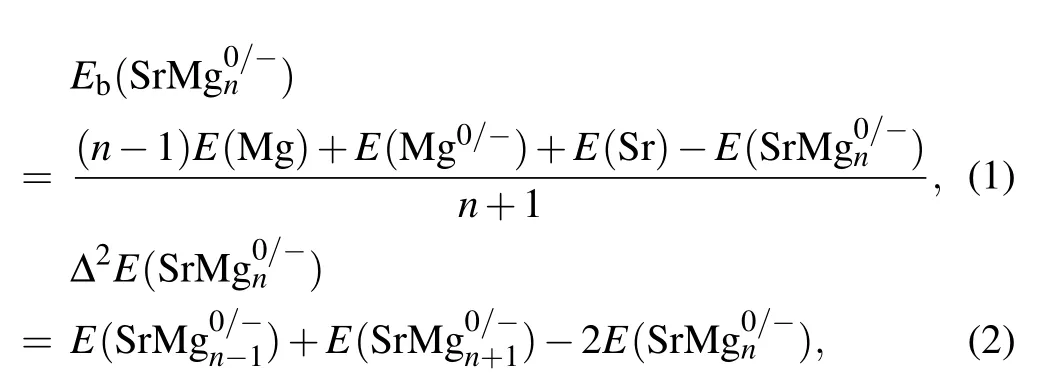
whereErepresents the total energy of the relevant clusters or atoms. According to the aforesaid formula,the specific calculated results are displayed in Fig.4. TheEbwhich refers to the average binding energy of clusters is the basis of reflecting the stability of clusters.[43-49]That is to say, the higher the value ofEb,the higher the stability is. From Fig.4(a)it follows that the values ofEbof anionic clusters are distinctly higher than those of neutral clusters.Furthermore,theEbvalues of anionic and neutral clusters increase monotonically,when n is from 3 to 9.

The total energy of the second-order difference clusters can indicate the stability of clusters.[50-55]The larger the value, the more stable it is. As shown in Fig. 4(b), the calculated Δ2Evalues suggest that anionic SrMg-3, SrMg-6and SrMg-9clusters as well as neutral SrMg3, SrMg6and SrMg9clusters are in possession of more distinct stability than their adjacent clusters.

Fig.4. Size-dependent(a)average binding energy Eb,(b)second-order difference of energy Δ2E,and(c)HOMO-LUMO energy gap Eg for SrMg0/-n(n=1-12)clusters.

The HOMO-LUMO (highest occupied molecular orbital-lowest unoccupied molecular orbital) gap, which is difined as the energy gap between the highest occupied and the lowest unoccupied molecular orbitals, can represent the ability of a molecule to participate in a chemical reaction to some degree. A large value of the HOMO-LUMO energy gap is related to an enhanced chemical stability. Figure 4(c)exhibits the calculated values of the gapEgof the SrMg0/-n(n=1-12)in detail,whereEgrepresents the HOMO-LUMO gap. Obviously, the simulated results ofEgin both neutral and anionic SrMgnclusters depend heavily on the size of the cluster. It can be clearly seen that the values of gaps between the anionic SrMgnare inferior to those of the corresponding neutral SrMgnclusters. The HOMO-LUMO gap for neutral species reaches its maximum values whenn=1, 3, and 10,indicating that it is more chemically stable. In the range ofn=5-12,the evolution ofEgof the anionic SrMgncluster is oscillating compared with that of the neutral cluster due to the presence of extra electrons.

3.4. Charge transfer

The analysis of the charge distribution on atoms can conduce to exploring the mechanism of charge transfer among the atoms of cluster.[56-58]In order to investigate the charge transfer between Sr and Mg atoms for the lowest energy structures of SrMg0/-n(n=2-12) clusters, natural population analysis(NPA)[59]is employed to obtain the charge on each atom of SrMg0/-n(n= 2-12) clusters. The results are presented in Fig.5. From Fig.5,we can see that the Sr atoms in the neutral SrMgnclusters are positively charged within the scope from 0.17 to 0.82 electrons, meaning that the charge in the neutral SrMgnclusters is transferred from the Sr atom to Mg frame,that is to say, Sr serves as an electron donor in all SrMgnclusters. The above phenomenon may occur because the electronegativity of Sr atom(0.95)is smaller than the electronegativity of Mg atom(1.31),which implies that the Mg atom is more capable of attracting electrons. The Sr atoms of the anionic SrMg-nclusters are negative whenn=1-2, while they are positive whenn=3-12, indicating that the direction of charge transfer will change atn=3. The value is almost zero in SrMg3cluster, showing that it is nearly no charge transfer from Sr to Mg atom in this case.Moreover,it is interesting that both neutral and anion SrMg9clusters have local maximum values. Combining the results of relative stability analysis in the previous section,we conclude that both SrMg9neutral and SrMg-9anion have high stability.

Fig.5. Size-dependent total charge on Sr atoms for both neutral and anionic SrMgn clusters.

3.5. Bonding characters

The analyses of molecular orbital,multi-center,bond,and bond order are of great significance in characterizing the bonding characteristics of clusters. Based on the previous discussion,the neutral SrMg9cluster which has a higher stability is selected as a representative example to detect bonding characteristics. Figure 6 shows the HOMO-LUMO gaps, molecular orbitals and the energy levels of the neutral SrMg9cluster.The HOMO energy is 1.64 eV lower than the LUMO energy for SrMg9cluster. The HOMO composition includes 22.97%of s atomic orbital (AO) of Sr atom and 29.43% of s AO together with 38.144% of p AO of Mg atom. The components of LUMO mainly include 37.53%Sr-s AO,11.46%Sr-p AO,9.56%Mg-s AO,and 30.80%Mg-p AO.

In order to further understand the bonding characteristics of the SrMg9cluster, the adaptive natural density partitioning (AdNDP) method which is particularly suitable to investigating the nature of the chemical bond, is ultilized to studyncentral double electron (nc-2e) bond systematically, where it can be considered to be delocalized ifnis greater than 2,otherwise it is a localized bond whenn=1 or 2. The structural diagrams with atomic markers, multicenter bonds, and occupation numbers(ONs)of SrMg9cluster are displayed in Figs. 7(a) and 7(b), respectively. From Fig. 7(b), seven 4c-2eσ-type bonds with bond orders of 0.3798,0.2114,0.3867,0.3867, 0.2114, 0.2114, and 0.2114 are formed by the 1-3-4-9 SrMg3unit (ON=1.95|e|) as well as the 7-9-5-10, 7-9-5-5, 3-6-10-8, 3-6-10-6, 4-8-10-6, 4-8-10-6 Mg4unit(ON = 1.87|e|). In addition, there are three 6c-2eπ-type bonds with ON=1.84|e|in SrMg9cluster. Their multi-center bond orders are 0.3757,0.3725,and 0.3725,respectively. For the Sr-Mg bond (ON=1.95|e|), the interaction between Sr and Mg is dominated mainly by the 5s orbital of Sr atom and the 3p, 3s orbitals of the Mg atoms. The Mg-Mg bonds are formed mainly by the 3s orbitals and relatively a small number of 3p orbitals of the Mg atoms,for the other 4c-2e bonds.For three 6c-2e bonds, the interaction of Mg-Mg originates from the 3s and 3p orbitals of Mg atoms. It is worth noting that non localized bond is found in SrMg9cluster.

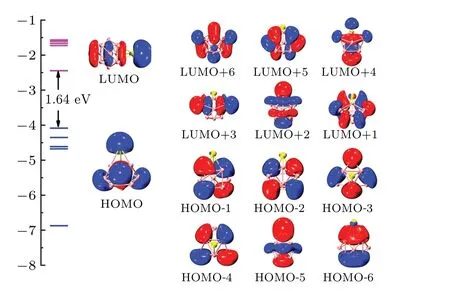
Fig. 6. Molecular orbitals and energy levels of neutral SrMg9 cluster, with HOMO-LUMO gap being denoted in black.

Fig.7. Analyses of(a)structural diagram with all atomic labels and(b)AdNDP chemical bonds and multi-center bond orders with occupation number(ON)for SrMg9 cluster.

4. Conclusions

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant No. 11404008), the Artificial Intelligence Key Laboratory of Sichuan Province, China(Grant No. 2018RYJ07), the Innovation Fund of Postgraduate Sichuan University of Science & Engineering, China(Grant Nos. y202007 and y2021008), the Innovation and Entrepreneurship Training Program of Sichuan Province,China(Grant Nos.S202010622080 and S202010622082),and the Innovation and Entrepreneurship Training Program of Sichuan University of Science & Engineering, China (Grant No.cx2019005).

The computation of this work was completed at Sichuan University of Science&Engineering High Performance Computing Center of Science&Engineering.