考虑平台佣金的制造商双渠道定价与渠道选择

罗列英 ,楼振凯

(1.温州商学院 管理学院,浙江 温州 325035;2.安徽工业大学 管理科学与工程学院,安徽 马鞍山 243032)

一、引言

随着电子商务的发展和普及,平台销售模式得到越来越多的顾客青睐。基于此,许多制造商利用直销模式优化其生产与销售策略,从而提高收益。电商平台带来的销售渠道,使制造商有更多的机会节省成本,增加收入,扩大新的细分市场。一般来说,线下零售提供了更好的购物体验和更多的选择空间,而平台直销通常送货上门从而省去了出门购物的时间和精力。因此,消费者对不同渠道的同种商品的购买偏好不一样。在双渠道定价决策中,偏好系数对于制造商和零售商的重要性在理论上已经得到论证。

近些年,由于实践中问题的多样性,关于双渠道定价的研究越来越多。林庆等通过分段函数描述消费者的购买行为,研究差异性批发价对双渠道的影响。Xiao et al.在制造商可能缺货的情形下,考虑了优先供应的问题,给出了优先供应直销渠道或零售商的判别条件。Ding et al.考虑了双渠道问题的联合定价策略,对等价策略、价格比拼策略等多种不同定价策略进行分析并比较对应策略下的收益。郭金森等对具有不同风险厌恶性的零售商和制造商之间的双渠道闭环供应链进行研究,分析在市场波动下收益的变化。Modak et al.将随机因素引入双渠道的需求函数中,研究了价格与交货时间相关的双渠道供应链问题,通过零售渠道的价格和订购量、直销渠道的价格与备货量以及直销渠道的交货时间,平衡缺货与过度生产。王文宾等研究了双渠道混合销售下制造商与分销商的定价和收益共享契约问题。

以上文献大多把平台渠道当作一个线上零售商进行处理,然而现实中很多电商平台如天猫、美团等是以收取佣金,由制造商确定直销价格的方式运营的。基于此,一些学者对平台佣金模式下的销售问题进行了分析。金亮等考虑了线上与线下的交叉销售行为,建立了涉及线上零售商和线下实体店的委托代理模型,并研究其佣金契约的设计。梁喜等对平台佣金模式下的制造商双渠道定价问题进行了深入探讨,分析了线下渠道、线上渠道和制造商利润与佣金率的关系,并研究了制造商的渠道选择问题。Wang et al.和王玉燕等将电商平台看作决策参与者,研究供应链的竞争和合作决策问题。

受上述文献的启发,本文对平台收取佣金模式下制造商双渠道定价问题进行研究。不过,已有文献对佣金率制定的合理性缺乏研究,天猫等电商平台对不同类商品制定了不同的佣金率,事实上不同的佣金率将影响制造商的定价决策,本文将深入探讨并给出理论依据。另外,对佣金率不合理时渠道的有效性问题进行了分析,类似Lou et al.的思路,讨论了这种情况下制造商的渠道选择决策。最后,本文给出了价格敏感强度的概念,并表明敏感强度的值决定了双渠道是否有效运行。

二、符号描述及假设

为了进行建模分析,首先给出必要的符号定义:

1.对一给定的有限长度销售周期,

a

为销售期内市场对商品的潜在需求。2

.p

为制造商(或供应商)给出的将商品批发给门店等传统渠道的批发价;

p

为由传统渠道确定的零售价格;

p

为由制造商确定的平台直销渠道的销售价格。决策的顺序为制造商先给出批发价

p

和直销价

p

,然后零售商确定订购量和零售价

p

。3

.c

为制造商单位商品的成本。虽然成本只是一个常数,但其影响制造商和零售商决策变量的确定,因此不考虑成本进行求解得到的结果,对实际问题缺乏足够的应用价值。4

.

传统渠道能现场挑选从而保证了商品的品质,而平台渠道提供了送货上门等服务,因此顾客对不同渠道存在不同的购买偏好。

λ

为顾客在传统渠道购买的偏好系数,1-

λ

为顾客在平台渠道购买的偏好系数,0<

λ

<1。5

.

由于本文考虑的因素较多,为了避免过多的符号计算,采用Lu et al.和唐飞等的处理,即认为不同渠道的需求对价格的敏感系数相同。

δ

为顾客需求对商品价格的敏感系数,

θ

为不同渠道之间价格的交叉影响因子,

δ

>

θ

>0。6

.

类似Lou et al.给出的双渠道需求表达,

D

=

λa

-

δp

+

θp

为传统渠道销售期内的销售量,

D

=(1-

λ

)

a

-

δp

+

θp

为平台直销渠道销售期内的销售量。7

.

对零售商来说,每次进货需要付出订购成本。对制造商而言,每次通过平台销售商品需要付出配送成本(如果选择让顾客出配送费,将使得最优直销价格降低,因而对制造商收益而言结果是一样的)。令

m

为零售商单位商品的订购成本,

n

为制造商通过平台销售单位商品的配送成本。由于订购是大批量而平台每次的销售往往数量较少,因此总有

m

<

n

。过高的配送成本将使得销售无法获得利润,本文假设

n

≤

c

。8

.β

为由平台给定的佣金率,过高的佣金率会导致制造商无法在销渠道获得净收益,即该渠道失去竞争力。实际中,不同种类的商品具有不同的佣金率,本文将探讨其理论依据。9

.W

为传统零售商销售周期内的净收益,

Z

为制造商双渠道销售的总利润。其中,制造商的净收益由批发给零售商所赚的利润和通过平台所赚的利润两部分组成。上述符号中,

δ

>

θ

保证了对任意大于零的价格下双渠道需求量之和

D

+

D

总是小于市场潜在需求

a

。如果

δ

与

θ

的值很接近,会导致两个渠道销售价都较高的情况下需求量

D

+

D

仍然接近市场潜在需求,可以认为此时市场对双渠道的价格不敏感。为了描述市场对双渠道价格的敏感性和便于探讨佣金率

β

对最优定价和渠道选择的影响,给出如下定义:定义1:令

k

=

δ/θ

为市场对双渠道价格的敏感强度,敏感强度越大,在相同的零售价和直销价下市场的实际需求越低。由于在最优解的合理性分析过程中,变量之间的大小关系十分重要,类似Lou et al.和楼振凯等的处理,给出现实中绝大多数情况下都能满足的一个变量关系。一般来说,商品的制造成本、订购成本和配送成本远小于商品售价,因此本文假设不等式

λa

-

δ

(

c

+

m

)>0 和(1-

λ

)

a

-

δ

(

c

+

n

)>0 总是成立的。

三、双渠道最优定价

在双渠道定价问题中,佣金率

β

看作常数,制造商需要确定批发给传统零售商的价格

p

和自己在平台上的销售价

p

,传统零售商只需要确定线下渠道的零售价

p

。为了使双渠道销售能够有效运行,考虑各价格的合理取值范围,对后续模型解的讨论至关重要。显然,要使双渠道销售能有效运行,需要满足合理价格的实际要求,即批发价

p

需满足

p

≥

c

,平台直销价

p

需满足(1-

β

)

p

≥

c

+

n

,线下零售价

p

需满足

p

≥

p

+

m

。接下来考虑双渠道同时有效运行的情况下,

p

和

p

的上界。为了使两条渠道都有需求量,

p

和

p

还需满足下列不等式组:

采用消元法求解上述不等式组得到:

由于表达式(1)是通过将两个不等式相加消元解得,因此是两条渠道都有需求量的必要非充分条件。也就是说,若

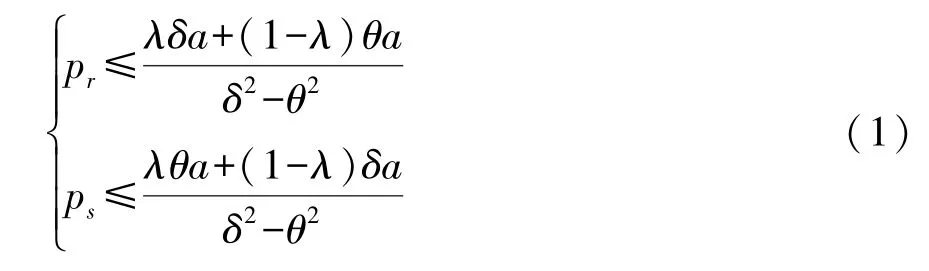
p

和

p

中有一个不满足不等式组(1),则至少有一条渠道需求量为零。

由于需求不可能为负数,因此在接下来的建模中,加入需求不为负的约束,防止最大化收益过程中出现两个负数相乘的情形而产生无效解。在制造商最大化收益的模型中,某条渠道需求为零意味着对制造商来说运行一条渠道是最佳的。

在考虑零售商的决策对其产生的影响的前提下,制造商最大化其净收益的模型为:

由于制造商先给出批发价和直销价,因此传统零售商的模型中不需要考虑批发价

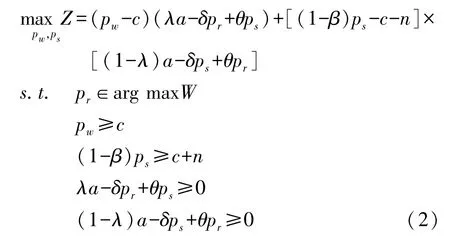
p

和直销价

p

的影响,其模型为:

不考虑确定区间的约束限制,对上述Stackelberg 博弈采用逆序求解。对任意的直销价

p

,由模型(3)得到零售商最优零售价

pr

的唯一表达:

由决策顺序可知,对该Stackelberg 博弈来说,只需要确定制造商的决策变量,传统零售商的最优定价也随之确定。

利用表达式(4),将模型(2)中目标函数转化为如下形式(约束条件不变):

对目标式(5)中

Z

关于

p

和

p

求偏导并令之为零,得到如下方程组:

表达式(7)给出的解是连续函数

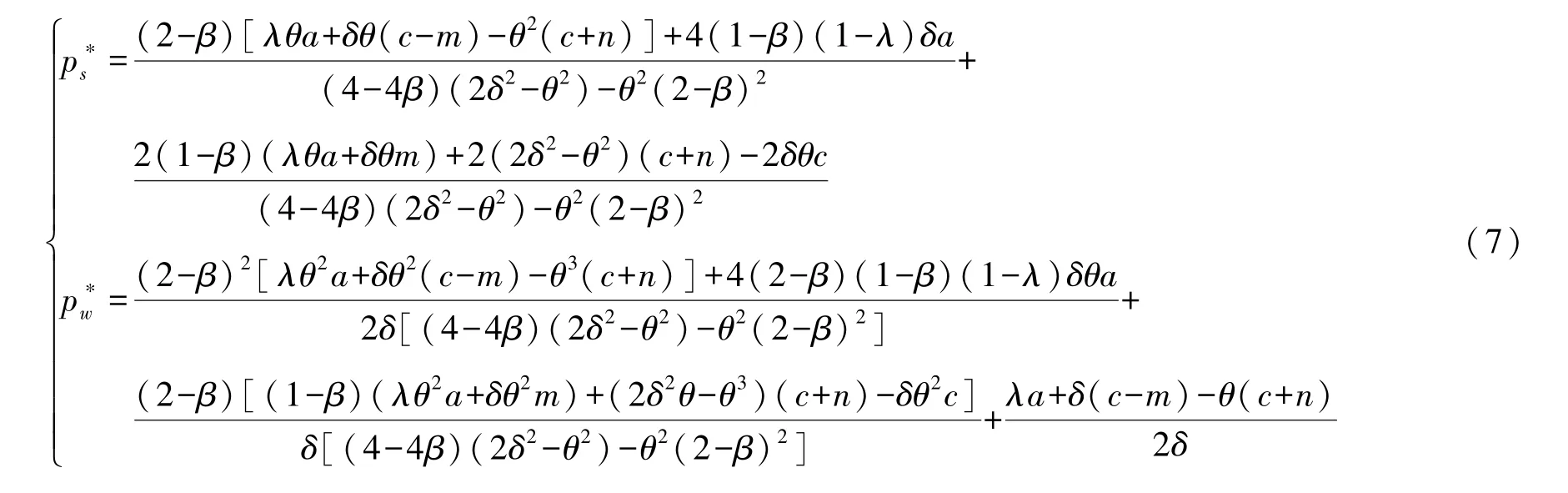
Z

的唯一可能的极值点。

Z

的黑塞矩阵为:

由于64

k

(2

k

-1)(2

k

-2)<(16

k

-12

k

)(2

k

-1)(2

k

-2),因此

f

(

k

)>0 恒成立,且

k

→+∞时,

f

(

k

)→1,即

f

(

k

)<1 成立。因此,要使

Z

的黑塞矩阵负定,在确定的市场强度

k

下,佣金率的取值必须满足:

此时表达式(7)给出的解是

Z

的唯一极大值点,通过偏导数的判断可知该极大值同时是

Z

的最大值,即制造商的最优定价唯一。根据已知条件,

δ

>

θ

,

m

<

n

≤

c

和

λa

-

δ

(

c

+

m

)>0 容易判断,此时由表达式(7)给出的最优批发价和最优直销价都为正数。事实上,考虑到

f

(

k

)的严格递增性,当敏感强度较大的时候,上述不等式约束是比较松的,比如当

k

=1.5 时,0<

β

<0.916;而当敏感强度较小时,该约束则比较严,比如当

k

=1.01 时,0<

β

<0.33。

实际应用中,天猫等电商平台对不同种类的商品设定了不同的佣金率,理论上来说也是由于不同类商品双渠道价格的敏感强度不同,过高的佣金率将使平台渠道失去盈利空间从而使得制造商放弃该渠道。

当

β

不满足不等式(9)的情形,或者说黑塞矩阵不定下的制造商最优定价,将在第四部分进行讨论。

四、解的合理性与渠道选择

分别分析佣金率

β

满足不等式(9)和不满足不等式(9)两种情况时,零售渠道的定价合理性和销售渠道的有效运行问题。当佣金率

β

满足不等式(9)时,意味着制造商和零售商的最优定价表达式唯一。下面分成几种情况,讨论线上和线下销售渠道的有效运行: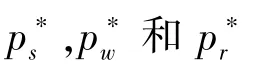

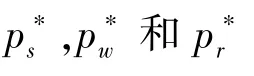
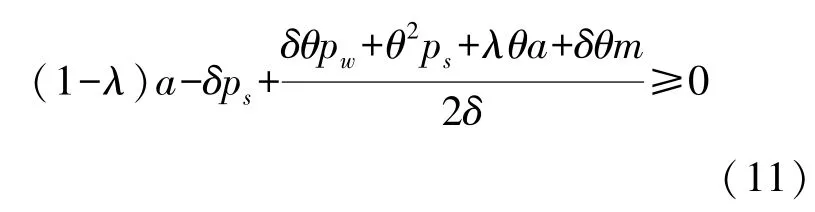
结合模型(2)和模型(11)可知,当某条渠道无法同时满足需求和差价为正的情况时,在最大化收益的目标下需求将取零。否则,在最大化收益过程中必将同时满足差价为正的约束。

当佣金率

β

不满足不等式(9)时,即目标式(5)的黑塞矩阵不定,此时目标函数无极值点。对一可导函数来说,若给定区间内无导数为零的点,则其最值必然在区间的端点取得,因此最大值点也就是目标式(5)的解将在模型(2)的某约束区间的端点取得。在不考虑平台渠道亏本运营的情形下(即

β

≥ 0),有如下结论:命题1:当佣金率

β

不满足不等式(9)时,模型(2)的解必然使得某个渠道的需求量为零。

对于佣金率

β

不满足不等式(9)时的情形,同样可以用模型(11)进行求解,其解必然满足命题1的结论。

五、算例分析

为了对本文提出的方法和得到的结论进行应用分析,给定如下参数设置:

λ

=0

.

6,

a

=300,

δ

=1.5,

θ

=1,

c

=40,

m

=10,

n

=20。

λ

>0

.

5 意味着当直销价和零售价相等时,更多的顾客倾向在可挑选商品的线下实体店购买。容易验证,上述参数满足

δ

>

θ

,

m

<

n

≤

c

,

λa

-

δ

(

c

+

m

)>0 和(1-

λ

)

a

-

δ

(

c

+

n

)>0 的假设。此时制造商收益函数黑塞矩阵负定的条件为0<

β

<0.916。

然后考虑佣金率

β

不满足不等式(9)时解的情况,设

β

=0.92。此时制造商对应的最大化收益模型:

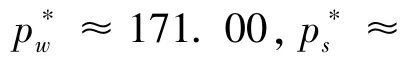
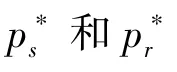
六、结论

本文在考虑生产成本、直销配送成本、零售商订购成本的情况下,深入研究了在制造商双渠道定价与渠道选择问题中佣金率与双渠道价格敏感强度的关系对最优解的影响,通过对解的分析可知,该关系式也是双渠道有效运行的充分条件。在对定价的合理性分析中,给出了无约束最优解合理的判别条件,并给出一个二次规划模型处理无约束解无效和无极值的情形。当制造商最优解使得某一渠道需求量(销售量)为零时,该渠道无法盈利。

由于涉及的符号较多,本文只考虑了一个制造商和一个零售商的情形。在接下来的研究中,将考虑平台作为博弈参与者确定最优佣金比例的问题,涉及三方博弈,形成一个三层串联式模型。此时将不得不考虑平台的单位产品运营成本,模型将变得较复杂。

另外,本文在建立模型的过程中没有考虑随机因素。事实上,当双渠道问题涉及随机因素时,制造商如何确定产量,平衡不同渠道的缺货与过度生产等问题十分关键。