海底滑坡中滑水效应的危害*

单治钢 廖哲贤 董友扣 王 栋 崔 岚

(①中国电建集团华东勘测设计研究院有限公司， 杭州 311122， 中国) (②海洋岩土工程勘察技术与装备浙江省工程研究中心， 杭州 311122， 中国) (③中国地质大学(武汉)， 武汉 430074， 中国) (④中国海洋大学， 青岛 266100， 中国) (⑤中国科学院武汉岩土力学研究所， 武汉 430071， 中国)

0 引 言

海底滑坡作为陆相沉积物向海相运移的主要方式之一，可以搬运大量由砂、黏土和碎石组成的沉积物(Hampton et al.，1996； 朱超祁等， 2016； 霍沿东等， 2019)。目前已知的最大规模海底滑坡Storegga滑坡体积超过5600 km3(Kvalstad et al.，2005)。与陆地滑坡相比，海底滑坡的滑动速度更快，可以高达35 m · s-1。滑坡体材料呈非牛顿流体特性，高速运动的滑坡体可以对下游构筑物(管线、缆线、防沉板和立柱等)造成严重破坏，并可能引发海啸等次生灾害(Coyne et al.，2005； Nodine et al.，2006)。解秋红等(2016)、修宗祥等(2016)和Dong et al.(2017a)采用数值方法反分析了海底滑坡的滑动过程。部分学者研究了海底滑坡对海底构筑物的冲击(王立忠等， 2008；Zakeri， 2009； Liu et al.，2015； Dong et al.，2017b， 2020a； 冯斌等， 2019； 王忠涛， 2019； Fan et al.，2021)，并基于此对构筑物的外形进行了优化设计(范宁等， 2018)。

海底滑坡的滑动距离远远大于陆上滑坡：比如 Storegga滑坡最远滑动距离达到810 km(Kvalstad et al.，2005)，而陆上滑坡的最大滑动距离仅为数十公里(朱超祁等， 2016)。滑水被认为是海底滑坡高速和长距离滑动的主要原因。滑水是指环境水侵入滑坡体下方形成水垫层，使滑坡体下的基床阻力远低于滑坡体的抗剪强度，滑坡体得以更大的速度向前滑动。Ilstad et al. (2004a)对大量的挪威海底滑坡案例进行反分析发现：滑水产生的水垫层阻力比滑坡体抗剪强度低一个数量级。滑水会引起滑坡体前端脱离主体，形成一系列独立的滑块。此类滑块整体性好、底部阻力小，因而滑动距离最远可达到数百公里。挪威FinneidFjord滑坡区域内发现了大量的独立滑块，证明了真实海底滑坡中滑水的存在(Ilstad et al.，2004a)。De Blasio et al. (2004)通过室内试验发现滑水发生后滑坡体的最大滑动速度可达到35 m · s-1，并推算出滑动距离可达到125 km。Elverhøi et al. (2005)采用数值模拟方法对Bear Land和Grand Banks两处滑坡分别进行反分析，发现滑水导致滑坡体的滑动距离增加约30%。

目前对海底滑坡有效的研究手段还比较有限。由于海底环境复杂，且海底滑坡具有不可预测性和瞬时性，尚无法实时追踪海底滑坡和滑水现象的全过程。现有研究主要通过物探技术获得海底地层剖面后对海底滑坡案例进行事件后分析(来向华等， 2000； 王磊等， 2016)，有相当的不确定性。室内试验可以借助高清摄像头和粒子图像测速(PIV)技术捕捉滑水的触发过程(De Blasio et al.，2004； Ilstad et al.，2004a)，但是严重的尺度效应问题限制了其应用范围。相比之下，数值分析为研究海底滑坡的滑水提供了更好的选择，已在现有研究中得到了一定的应用(Mohrig et al.，1998； 王立忠等， 2008)。

现有考虑滑水的海底滑坡模拟主要采用深度平均法(Imran et al.，2001)，将滑坡体简化为插塞层(Plug layer)和剪切层(Shear layer)，对插塞层内滑坡体的滑动速度沿深度进行平均，可将三维或二维滑坡问题简化为二维或一维问题。因而该方法计算效率较高，特别适用于大规模海底滑坡问题。然而，该方法仅能考虑滑坡体的连续塑性变形，不能模拟滑水造成的滑坡体前端脱离主体并形成独立滑块的过程(Dong et al.，2020b)，因而不适用于模拟滑水作用下海底滑坡的滑动全过程。

本文采用一种新型数值方法物质点法(MPM)模拟海底滑坡的滑动过程，考虑滑水对基床阻力的影响，分别对室内试验和真实的海底滑坡案例进行反分析，评估滑水对海底滑坡的危害范围和滑动形态的影响。

1 滑水的作用机制及其数值实现

1.1 滑水的作用机制

滑水的作用机制是一个复杂的多学科交叉问题，其困难性导致目前对于滑水的针对性研究还比较少(Huang et al.，1997)，国内更是未见报道(余斌， 2007； Liu et al.，2020)。国际上De Blasio et al.(2004)和Harbitz et al.(2003)采用改进的润滑理论分析了滑水触发的力学机制，为后续研究奠定了理论基础。

对海底滑坡的滑动过程进行简化分析，将滑坡体考虑为连续的黏弹性材料，假设一个平面滑坡体沿刚性海床滑动，滑坡体主要受到自身浮重和水体拖曳力的影响，其中自身浮重垂直于海床方向的分量控制滑坡体的沉积过程，自身浮重沿顺坡方向的分量控制滑坡体向前滑动的动力过程。滑坡体所受阻力主要包括基床阻力τB、环境水施加的拖曳阻力τD和前端动水压力fp。其中基床阻力τB主要由基床土体抗剪强度提供，如图1所示。滑坡体顶部所受到拖曳力计算为：

(1)

式中：ρw是环境水的密度(ρw=1000 kg · m-3)；CF是一个常数，文献(De Blasio et al.，2004)建议取值为0.003～0.005；u是滑坡体的滑动速度。前端动水压力为：

(2)

式中：CP是一个常数，其取值可由文献(Newman， 1977)查得。前端动水压力部分主要影响滑坡体的形态，对滑坡体的动力特性影响较小，因此本文中不予考虑。

运动过程中，滑坡体前端趾部滞点处受到环境水的动水压力最大，可计算为：

(3)

当该动水压力大于滑坡体前端的浮重时，滑坡体前端上翘，部分环境水侵入滑坡体底部，逐渐形成水垫层：

(4)

式中：ρ是滑坡体的密度；D是滑坡体厚度；g是重力加速度；θ是坡度。式(4)可变形为：

(5)

式中：Fc是一个表示滑水触发时机的常数，文献(De Blasio et al.，2004)根据一系列小尺度室内试验测得该常数通常为0.3，而对于现场真实滑坡案例可取值为1。式(4)表明，滑水发生时滑坡体的滑动速度必须大于某一个临界速度。当滑水发生后滑坡体底部的阻力由水垫层提供，因而其数值为：

(6)

式中：μw是水垫层的黏性，文献(De Blasio et al.，2004)中取值为0.01；Dw是水垫层的厚度；fw是水垫层的消散量，用于表征水垫层维持的时间，本文中不予考虑。

图 1 滑坡体受力示意图Fig. 1 Schematic for sliding mass

1.2 滑水的物质点法实现

物质点法是任意拉格朗日-欧拉法的一种，采用拉格朗日物质点描述材料的历史信息(质量、体积、密度、速度、变形梯度和应力等)，并在欧拉网格上求解控制方程(de Vaucorbeil et al.，2020； Nguyen et al.，2020；Sun et al.，2020；Yuan et al.，2021)。物质点法的主要计算步骤包括： (1)物质点向网格节点投影； (2)计算网格节点速度和加速度； (3)更新物质点的应力和其他状态信息； (4)更新物质点位置。计算前，将滑坡体材料离散为一系列物质点，将计算区域划分成网格单元。计算时，首先将物质点上的速度、质量、体积和应力等信息投影到网格节点上，在节点上建立平衡方程求解出下一时步的速度场，之后将新的速度和加速度投影给物质点，用于更新其运动状态和变形、应力等信息。计算过程中，网格节点上的信息都为临时信息，不保存任何历史信息。网格在空间中的位置固定，不会像传统有限元法单元那样随着材料的运动而发生变形，避免了网格畸变的问题，因此非常适合处理海底滑坡在滑动过程中的大变形问题(Soga et al.，2016；Yerro et al.，2016； 厉成阳等， 2018)。

本文中的分析基于自主开发的物质点法程序MPM-GeoFluidFlow，基于显式积分采用二次形函数进行插值求解，采用柯西应力描述应力状态，应力增量采用Jaumann率表述以遵从有限应变原理。该程序的特色功能有3项： (1)对程序进行大规模GPU并行(Dong et al.，2015， 2018)，计算效率较CPU单核模拟最大提高约900倍； (2)采用先进的接触算法Geo-contact(Ma et al.，2014)，在土体-结构物接触的模拟中可以得到平滑的接触反力； (3)对变形过大出现空隙或团块的物质点重新生成(Dong， 2020)。

与传统的CPU相比，GPU拥有更多的计算核心和更强的批处理能力，因此具有更好的并行加速潜力。然而，GPU并行的架构与CPU并行差异较大，已有CPU并行的程序并不能直接移植到GPU平台，因此，需要对程序架构进行重新设计，以最大程度发挥GPU计算核心的效力。并行过程中，需要特别注意保持各个计算线程之间的相互独立性，防止出现显存访问竞争问题。GPU显存到主机内存之间数据传输速度较慢，因此，并行计算时，首先将所有变量传输到GPU的显存中，以避免频繁的变量传输。对于计算步(2)和(3)，每个节点的信息更新均采用一个核心进行计算，所有核心的计算同时进行，由于相互之间有较好的独立性，因此具有良好的可并行性。类似的，对于计算步(4)，每个物质点的信息更新采用一个核心进行计算，并将所有核心同时进行并行计算。但对于计算步(1)，传统的线行计算中一般将不同的物质点信息依次投影给周围的节点，直接用到并行计算中时会产生线程间的相互干扰。本文程序采用的解决方案是首先建立每个网格节点对应的物质点列表，在并行计算中将每个节点的投影计算进行线行计算，对不同的节点进行并行计算(Dong et al.，2015， 2018)。

(7)

式中：Ai和mi分别是节点i所表征的面积和质量； Δt是时间步长:

(8)

式中：G和λ分别是剪切模量和拉梅常数；d为网格尺寸；α为系数。

2 室内水槽试验

小尺度的室内水槽试验可简化海底滑坡滑动过程中复杂的海底环境，对主要控制因素进行精细化还原，因而可用于复现海底滑坡滑水效应的发生过程。本文中模拟的室内水槽试验包含陆上滑坡(无水环境)和海底滑坡(有水环境)两组对照试验(De Blasio et al.，2004)。水槽在长度5.7 m内坡度为5°； 在此距离(坡折点)以外坡度减小至1°。滑坡体材料的初始形状为高0.11 m，长2 m，截面积0.15 m2的椭圆形。滑坡体材料表观密度为1600 kg · m-3，抗剪强度与剪切应变率关联并考虑强度软化的影响(范宁等， 2018):

(9)

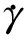
陆上滑坡在滑坡体的自重(ρgcosD)驱动下向前滑动，并受到基底的摩擦阻力，最终滑动距离约为5 m，在坡折点(5.7 m)前停止，最终滑动形态如图 2 所示。5 s时滑坡体的速度云图如图 3 所示。

图 2 小尺度水槽试验滑动距离Fig. 2 Small-scale flume test results

图 3 陆上滑坡体速度云图(时刻5 s)Fig. 3 Velocity contour for subaerial sliding mass(time 5 s)

对于水下滑坡，滑坡体在环境水的浮力作用下所受的自重驱动力((ρ-ρw)gcosD)较小。若不考虑滑水的作用，其滑动距离仅为约0.7 m (图 2)。而在试验中水下滑坡的滑动距离长达7.5 m，其主要原因是发生了滑水现象。考虑不同的基底阻力τB，进行参数分析，得到了不同的最终滑动距离S：τB=36 Pa，S=1.2 m;τB=20 Pa，S=6.4 m;τB=18 Pa，S=7 m。其中：当τB=18 Pa时，滑坡体最终滑动距离与试验中最为接近。由此可见，试验中滑坡体所受到的基底阻力平均值约为18 Pa，该值远小于滑坡体的抗剪强度初始值。采用式(5)考虑滑水的触发时机，其中，Fc取值为0.3。当滑坡体发生滑水时滑坡体底部的阻力由式(6)计算得到，最终预测的滑动距离与试验较接近，为8.4 m。

通过上述对比可发现，物质点法可较好地模拟海底滑坡的大变形滑动过程，能够有效地复现滑水的触发和发展过程，在预测滑坡体的滑动距离方面有较高的精度。相比之下，DAM方法由于对速度进行深度平均的先天不足，无法准确预测滑动过程中滑坡体的速度分布，在对具体案例进行分析时限制性较大。考虑海底滑坡过程中的滑水时，滑坡体前端滑动速度远大于滑坡体尾部，因而物质点法模拟结果中滑坡体前后出现分离现象。该现象在试验中也被观测到(图 2)，在真实滑坡中分离的滑坡体前端部分将会形成若干离散的块体分布在滑坡的运动轨迹上。文献(De Blasio et al.，2004)的DAM分析中仅考虑滑坡体为连续体，因而未能反映滑坡体的分离现象，由此可见，在海底滑坡的滑动模拟中，物质点法比DAM方法更具优势，而DAM方法主要用于海底管线路由设计中粗略估计潜在海底滑坡影响范围，且不能对海底滑坡和管线的相互作用进行分析(王立忠等， 2008； Zakeri， 2009； Liu et al.，2015； Dong et al.，2017b， 2020a； 冯斌等， 2019； 王忠涛， 2019)。滑动过程中(5 s)滑坡体的速度分布如图 4 所示，滑动全过程中滑坡体的速度与位移时程变化趋势如图 5 所示。

图 4 水下滑坡体速度云图(时刻5 s)Fig. 4 Velocity contour for submarine sliding mass(time 5 s)

图 5 滑坡体速度位移时程曲线Fig. 5 History of velocity and displacement of sliding mass

3 真实滑坡案例分析

一处真实的岸坡垮塌造成的海底滑坡发生在北挪威的Finneidfjord湾区，超过百万立方米的土体发生了位移。关于事件后的沉积物性状和滑动区环境特征等详见文献(Ilstad et al.，2004b)，调查结果显示该滑坡主要由浅层气体造成。整个滑坡区域可以划分成4小块，如图 6 所示。其中沉积物主体分布在A区域，该区域在滑坡体原始位置的1 km范围内，坡度约2.86°； 在A区域以外，散布着不同尺寸的滑出块体，其中最大的块体尺寸110 m×60 m×2 m，体积约1.2万立方米，最终在D区停止。区域B和C的坡度分别为0.94°和0.46°。对现场海床土体进行钻孔取样并分析得出，土体的软化系数为5～35，原状土不排水抗剪强度为10～15 kPa。根据地质条件综合分析表明，滑水是造成滑坡体超远滑动并分离成离散滑块的主要原因。

图 6 Finneidfjord滑坡地形图和沉积物抗剪强度(Ilstad et al., 2004a)Fig. 6 Morphology and sediment strength in Finneidfjord slide(Ilstad et al., 2004a)a. 滑坡区分为4个区域; b. 滑出块体不排水抗剪强度

物质点法分析中，原始滑坡体简化为高度25 m，上底30 m，下底110 m的梯形平面体，单元尺寸0.25 m。原状土强度15 kPa，软化系数为10。滑坡体材料浮密度为500 kg · m-3。模型底边界模拟海床表面，初始为无滑动边界，发生滑水时为部分滑动边界。模型两侧和上边界皆为自由边界。滑坡体的杨氏模量为500su0，泊松比为0.49，重力加速度g=9.81 m · s-2。由于本构模型存在分叉不连续问题，因此对于具有强烈应变软化特性的土的计算往往会受到网格依赖性的困扰(图 7)。本文的计算中发现，采用网格尺寸0.25 m和0.125 m时滑坡体前端滑出块体的运动机制一致，对计算结果不会产生过大影响，如图 7 所示。当不考虑滑水效应时，滑出块体长约70 m，高约9 m。滑出块体在A区(0～1 km)内驱动力约为2.2 kPa，高于基底阻力(1.5 kPa)，因此滑块始终保持加速，但速度较小，仅为0.2 m · s-1左右(图 8a)； 当滑块进入B区后(1～1.2 km)，其内驱动力约为0.7 kPa，低于基底阻力(1.5 kPa)，因此滑块始终保持减速，很快在B区停止。考虑滑水效应后，滑出块体所受基底阻力主要由水垫层提供，其数值约为350 Pa，低于滑块在A、B、C区中的驱动力，因此滑块始终保持加速，最终在D区由于地形变化而停止。考虑滑水效应后，滑坡体最大滑动速度可达17 m · s-1(图 8b)，并最终在C区中部停止(图 9)。在滑出块体滑动沿程，可见滑坡体变形产生的明显滑动痕迹。

图 7 不同网格尺寸对滑动距离和滑动形态的影响Fig. 7 Influence of mesh size on runout distance and morphologya. 网格尺寸0.25 m(1000 s); b. 网格尺寸0.125 m(1000 s)

图 8 滑水对滑坡体滑动距离和滑动形态的影响Fig. 8 Influence of hydroplaning on runout distance and morphologya. 无滑水； b. 有滑水

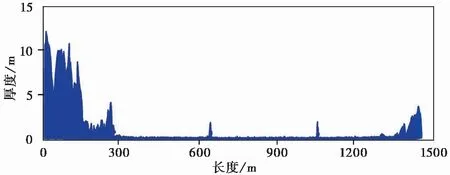
图 9 考虑滑水效应时滑坡体的最终形态Fig. 9 Final morphology of sliding mass with hydroplaning

对比物质点法计算结果和真实滑坡遗迹可发现，物质点法模拟中考虑滑水效应时滑坡体的最远滑动距离与真实距离较接近，进一步表明物质点法具有较高的准确性和可靠性。尽管应变软化本构模型具有网格依赖性的不足(其他数值方法中也同样存在此问题)，不能准确捕捉滑坡体的最终形态，但是前端滑块的滑动特性较接近，最终预测的滑块最远距离有较高的可信度。对比分别考虑和不考虑滑水效应的模拟结果发现，滑水效应是Finneidfjord滑坡中滑坡体具有高动力性能的主要原因，进一步验证了前人研究中关于滑水效应的重要性和危害性的分析。

4 结 论

物质点法是一种新型数值方法，通过追踪物质点的移动描述材料的变形过程，可以有效地模拟海底滑坡等大变形问题。本文采用自主研发的物质点法程序MPM-GeoFluidFlow模拟海底滑坡的滑动过程，考虑滑水对基床阻力的影响，分别对室内试验和真实的海底滑坡案例进行了反分析。主要结论如下：

(1)通过对比有滑水和无滑水条件的计算结果，验证了滑水是海底滑坡超远距离和超快速度滑动的主要原因，并据此评估了滑水对海底滑坡危害范围和滑动形态的影响，为实际工程中的应用提供了便利。

(2)计算结果进一步验证了物质点法在模拟海底滑坡的滑动过程时的可靠性和精确度，为相关类似研究提供了参考。