考虑波致孔压累积与应力耦合效应的埋置管线周围海床响应特征与机制分析*

刘小丽 李乔花 廖周全

(①山东省海洋环境地质工程重点实验室， 青岛 266100， 中国) (②中国海洋大学， 环境科学与工程学院， 青岛 266100， 中国)

0 引 言

海底管线常被称为海洋油气资源开发中的“生命线”，其安全问题历来受到众多研究者和海洋工程设计人员的关注。极端气候下风暴潮掀起的巨浪会导致管线周围海床的液化进而造成海底管线的失稳破坏(张衍涛， 2009; 付长静等， 2014)，因此较多文献对波浪作用下海底埋置管线周围海床的响应及液化特征进行了计算研究。当海床土渗透系数相对较小而波浪荷载相对较大时，波浪循环荷载下海床土的塑性变形会引起超孔隙水压力的不断累积，当某一深度的累积孔压超过其上覆有效应力时，即引起该深度位置海床土的液化，进而威胁管线的安全。

目前波浪作用下海床累积响应的计算方法主要有两种，第1种方法是直接利用弹塑性本构模型来模拟循环荷载下孔压的累积过程(Dunn et al.，2006;Ye et al.，2015; 王小雯等， 2018)，该种方法相对较为复杂，本构模型的描述需要大量不易测试的参数，因而其应用受到一定限制； 另一种方法是将循环剪切试验得到的半经验孔压累积源项表达式与渗流连续方程相结合以计算累积孔压的发展过程(Seed et al., 1978)，该种方法因计算简便参数较少而得到了较多应用(McDougal et al.，1989; 李小均等， 2009;Sumer et al.，2012)。基于孔压累积源项的方法虽然简单，但由于其未考虑累积孔压与海床应力的耦合效应，可能会导致计算结果出现较大偏差，因此，Liu et al. (2019)基于该方法的计算思想，提出了一种能够考虑累积孔压与海床应力耦合发展的计算模型，且未增加额外的计算参数。

基于孔压累积源项计算海床累积响应的方法已经被应用于波浪作用下管线-海床系统的响应分析中(Zhao et al.，2014; Foo et al.，2019)，但均未考虑累积孔压与海床应力的耦合效应。波浪作用下孔压累积与海床应力的耦合效应对埋置管线周围海床累积响应及其液化特征的影响如何，目前还未见相关的分析研究。为此，基于Liu et al. (2019)提出的计算模型，考虑累积孔压与海床应力的耦合效应，对非线性行进波作用下埋置管线周围海床土的累积响应特征进行模拟计算，并通过与不考虑孔压累积与海床应力耦合计算结果的对比分析，揭示累积孔压与应力的耦合效应对海底埋置管线周围海床累积响应特征的影响及其作用机制。

为了阐述方便，文中将未考虑孔压累积与海床应力耦合的累积响应计算模型称为“非耦合模型”，而将能够考虑孔压累积与海床应力耦合发展的海床响应计算模型称为“耦合模型”。

1 数值模型

波浪作用下含埋置管线的海床响应计算示意图如图 1 所示，其中：h为海床厚度，d为水深，H为波高，管线埋置在海床水平方向的中间位置，D为管径，e为埋深(指管线中心到海床表面的距离)。波浪在海床表面沿x轴正方向传播，海床土视为均匀各向同性的多孔弹性介质。

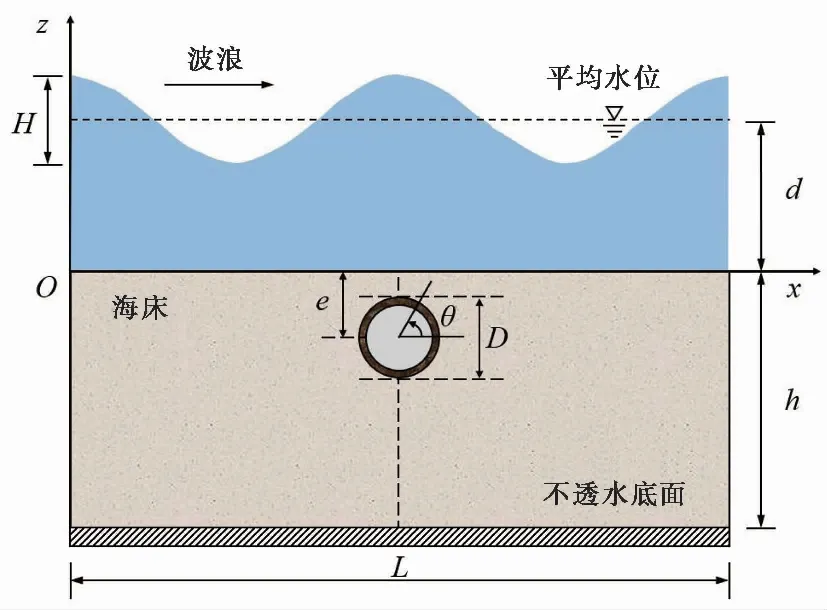
图 1 波浪作用下含埋置管线海床计算示意图Fig. 1 Sketch of the wave-induced seabed response around a buried pipeline

1.1 海床响应控制方程

海床响应耦合计算模型的控制方程推导详见Liu et al. (2019)的文献，此处给出其控制方程为：

(1)

(2)

(3)

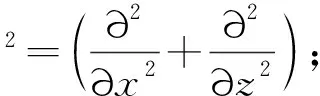
(4)

式中：Kf为孔隙水的弹性体积模量，Kf=2×109N·m-2；Sr为海床土体的饱和度；P0为绝对静水压力。

mv为海床土的体积压缩系数，可表示为：

(5)

ψ为累积孔压增长函数(孔压累积源项)，可表示为：

(6)

式中： |τmax|为海床周期最大剪应力；T为波浪周期；α=0.34Dr+0.084，β=0.37Dr-0.46，均为与海床相对密度有关的孔压累积计算参数；Dr为土体相对密度；σ′0为初始平均有效应力。

对于含埋置管线的海床，管线自重会影响周围海床的初始平均有效应力，因此，σ′0表达式为(Zhao et al.，2014)：

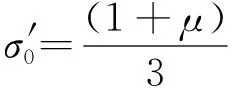
(7)

式中：σ′x0和σ′z0分别为重力作用下海床土的水平向和竖向有效正应力。

根据相关文献(Jeng et al.，2015)，非耦合模型海床的控制方程为：

(8)

式中：pres为波致累积孔隙水压力，其余符号同上述。

1.2 管线计算控制方程

管线为弹性体，其平衡方程为：

(9)

(10)

式中：up、wp分别为管线的水平位移和竖向位移；Gp和μp分别为管线的剪切模量和泊松比。

1.3 边界条件

考虑波浪的非线性特征，采用二阶Stokes行进波。在海床上表面，波致孔隙水压力为海床表面的波压力Pb(x，t)，其表达式为(Jeng et al.， 1997)：

Pb(x，t)=P0(C11cos(λx-ωt)+C02+

C20cos 2(λx-ωt)+C22cos 2(λx-ωt)

(11)

C11=1

(12)

(13)

(14)

(15)

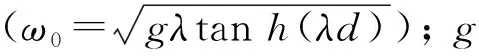
海床底面为不透水刚性边界，土体位移和孔隙水压力竖向梯度均为0，即∂p/∂z=u=w=0； 海床两侧为周期性边界； 管线表面为不透水边界，即∂p/∂n=0； 设管线与周围海床土共同位移，即管土边界的位移保持连续。

已有研究表明，海床液化后对波浪的传播具有一定的衰减效应(Tong et al.，2018)，因而当海床液化后，液化区海床土的性质以及海床表面的边界条件都会发生一定的变化，如何考虑这种变化，尚待更深入的理论与试验研究，本文同目前绝大部分文献的处理方式相同(Ye et al.，2015; Foo et al.，2019)，暂对此不作考虑。

1.4 模型的求解

利用Comsol Multiphysics多场耦合有限元分析软件建立数值计算模型并求解，耦合模型在求解过程中孔压累积源项中的最大剪应力项随着波浪作用时间而进行周期性更新。由于管线的存在会影响其周围海床土体响应，因此管线及其周围土体区域为重点研究区域，此部分的网格进行了局部加密，如图 2 所示。

2 模型验证

为了验证数值计算模型的可靠性，将本文的计算结果同Turcotte et al. (1984)的波浪水槽模型试验结果进行了对比，试验中海床和管道参数见表 1，3组波浪参数分别标注在图 3 中； Cheng et al.(1986)也利用与此试验参数进行了数值计算结果的对比验证，对比结果如图 3 所示。

表 1 试验参数Table 1 Parameters of the flume test

从图 3 中可以看出，本文数值模型计算得到的结果与试验结果(Turcotte et al.，1984)以及文献中数值计算结果(Cheng et al.， 1986)吻合较好，表明了本文数值计算模型的可靠性。

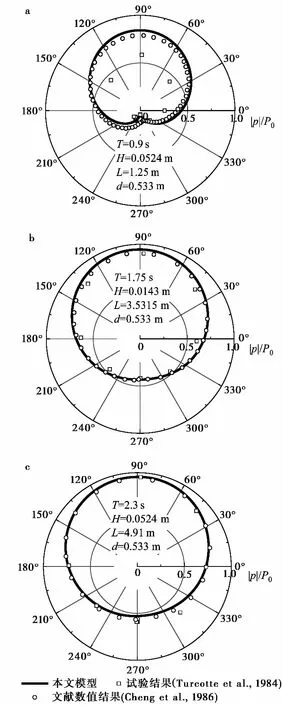
图 3 波浪作用下埋置管线周围孔压对比图Fig. 3 Comparison of wave-induced pore pressure around a buried pipeline

3 结果与讨论

考虑管线自重对海床初始应力场的影响，利用耦合模型和非耦合模型分别对波浪作用下含埋置管线的海床响应进行模拟计算，并通过对比分析，揭示管线周围海床土响应特征与机制。根据近海区域可能出现的极端波浪条件和海床土特征(常方强， 2009； 李佳峻等， 2017)，数值模型计算参数见表 2。

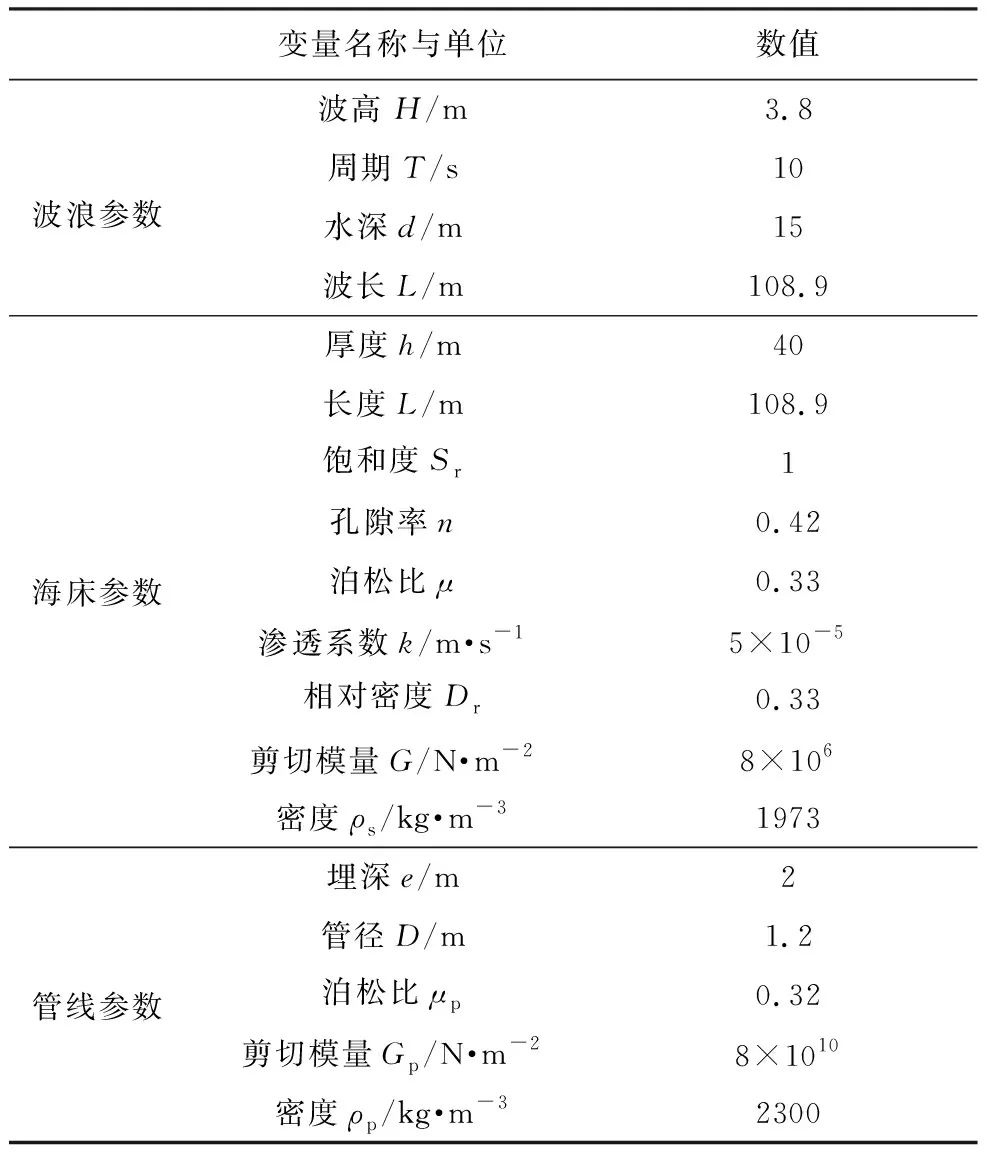
表 2 数值模型计算参数Table 2 Parameters of the numerical model

图 4 海床初始竖向有效应力分布图Fig. 4 Isosurface of the initial vertical effective stress

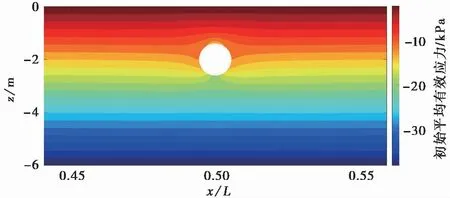
图 5 初始平均有效应力分布图Fig. 5 Isosurface of the initial mean effective stress

3.1 管线影响下的海床初始应力场

为考虑管线自重对海床初始应力场的影响，首先计算重力作用下含埋置管线海床的初始应力场，结果如图 4 和图 5 所示，分别为管线周围海床的初始竖向有效应力与初始平均有效应力等值面分布图(应力以拉为正，压为负)。

由图 4 和图 5 可以看出，受管线自重的影响，管线周围海床的初始应力不再是简单的线性分布，与无管线时相比，管线顶部和底部周围海床的初始竖向有效应力和平均有效应力均有所增加，而在管线两侧靠近管线处则有所减小，例如，管线底部初始竖向有效应力由无管线时的25 kPa增加为现在的30 kPa，增加量为20%。海床的初始应力场对于累积孔压的发展和海床液化都有重要影响，经数据分析可知，在距离管线边界约1.8 m处，管线自重对海床应力的影响小于5%，可知管线自重的影响范围约为距管线中心2倍管径(2D)的区域。

海床初始应力场会影响孔压累积源项，进而会对累积孔压的发展产生影响(Zhao et al.，2014)，因此，本文基于上述考虑管线自重影响的海床初始应力场进行累积孔压的发展计算。

3.2 管线周围海床累积孔压响应特征与机制

3.2.1 海床累积孔压发展特征

如图 6 所示，为管线顶面、底面和侧面各点以及相对应的远端各点(远点，即不受管线影响的区域)累积孔压随时间的发展曲线。耦合模型的计算结果表明，管线周围各点海床的累积孔压发展速度均远快于同一深度远端各点的累积孔压发展速度； 而非耦合的计算结果表明，管顶接触点(点1)位置累积孔压的发展速度小于其对应远点(点2)累积孔压的发展速度； 管中接触点(点3)与其对应远点(点4)的累积孔压发展速度差异不大； 管底接触点(点5)累积孔压的发展则快于其远点(点6)处，至100个波浪作用周期(100T)时，两者的累积孔压相差约4 kPa。同时，可以发现，无论是管线周围还是远端各点，考虑累积孔压与海床应力耦合效应时的累积孔压发展速度均快于非耦合模型，且两种模型的计算结果在管线周围各点处的差异相对更为显著，例如，在管底接触点处，波浪作用100T时耦合模型的累积孔压相对于非耦合模型增大了约19%，而在对应远点处耦合模型的累积孔压较非耦合模型增大约6%。

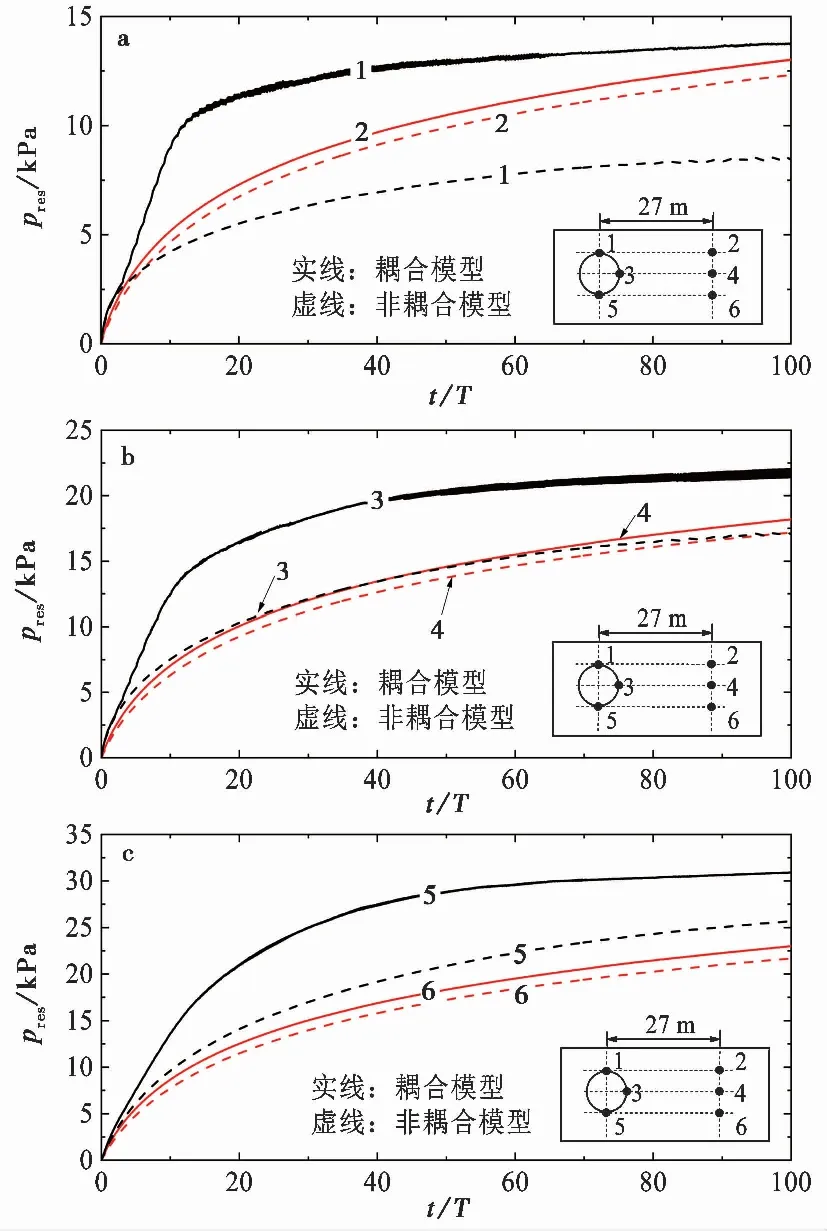
图 6 不同位置处累积孔压随时间变化对比图Fig. 6 Comparison of development of residual pore pressures at different locations

两种计算模型下累积孔压的水平分布和发展特征，可以在图 7 中得到更为清晰的展示。如图 7 所示，耦合模型下管线对海床累积孔压的发展影响相对较大，一方面管线周围累积孔压的数值远大于远端各点，另一方面，水平方向上管线对累积孔压的影响范围随着波浪作用时间的增加而有所增大，例如，当波浪作用时间为10T时，管底处的累积孔压为13.6 kPa，远点处为8.6 kPa，管底处的累积孔压相对于远点增大了58%，此时水平方向管线的影响范围共约14D； 当波浪作用时间为40T时，管底处的累积孔压为27 kPa，相应远点的累积孔压为16.6 kPa，管底处累积孔压相对于远点增大了63%，此时水平方向管线的影响范围约32D。非耦合模型的计算结果表明，管线对累积孔压的影响相对较小，首先，管线周围累积孔压的数值与远端相比差异较小，其次，水平方向上管线的影响范围也相对较小，且该影响范围基本不受波浪作用时间的影响，例如，波浪作用时间为10T和40T时，管底处累积孔压分别为9.4 kPa和19 kPa，相对于远端累积孔压均增加了约22%，且水平方向上管线的影响范围约为9D。累积孔压在管线顶面和中部水平截线上的分布特征与管线底部截面基本一致，只是在管线顶部端点处的累积孔压相对有所减小，具体如图 7 所示。

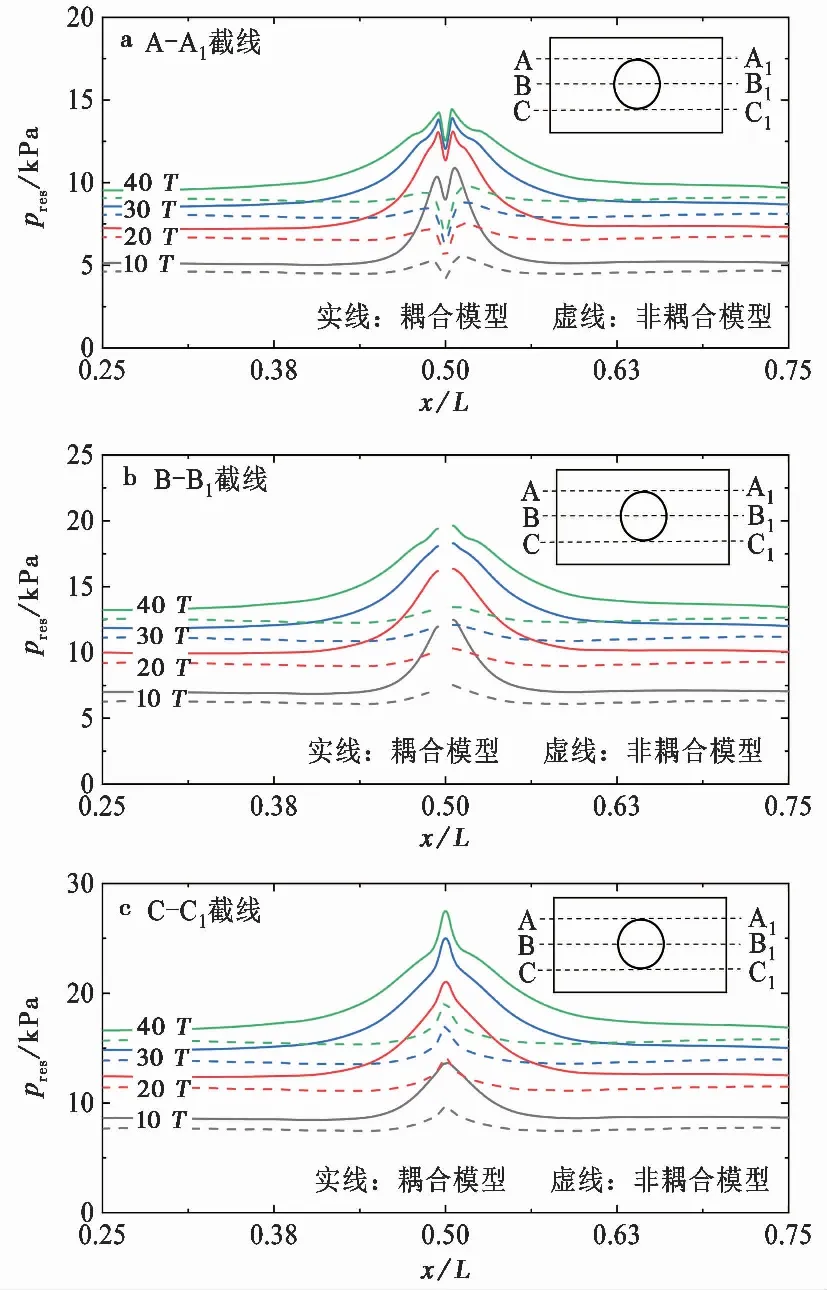
图 7 管线附近海床的累积孔压水平分布图Fig. 7 Lateral distribution of residual pore pressure in the vicinity of the pipeline

耦合模型与非耦合模型下累积孔压沿深度的分布特征如图 8 所示，图 8a和图8b分别为耦合模型与非耦合模型下管线中心竖向截面与远端海床竖向截面的累积孔压分布曲线。从图 8 中可以明显看出，当考虑海床应力与累积孔压的耦合效应时，管线周围海床的累积孔压明显增大，且竖直方向上管线对累积孔压的影响范围随着波浪作用时间的增加而有所增大，波浪作用为10T时管线对其下部海床累积孔压的影响深度约为6D，当波浪作用时间为40T时，管线对其下部海床累积孔压的影响深度扩大至18D。而当不考虑海床应力与累积孔压的耦合效应时，管线对其下部海床累积孔压的影响深度约为2D，其影响深度相对较小且基本不随波浪作用时间而变化。

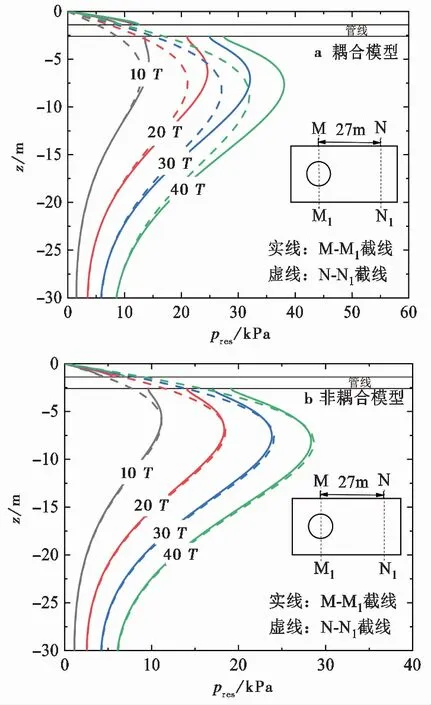
图 8 管线中心竖向截面与海床远端竖向截面的累积孔压分布对比图Fig. 8 Comparison of residual pore pressures along the vertical section across the central of the pipeline and that in the far field

沿管土交界面的海床累积孔压分布如图 9 所示，耦合模型与非耦合模型的计算结果均表明，管周下半部分海床的累积孔压均较其上半部分发展更快，其中尤以管线底端点处孔压的累积最为显著，例如，考虑累积孔压与海床应力的耦合效应， 30T时管线底端点累积孔压相对于10T时累积孔压的增加量为83%，而管线顶端点处的相应累积孔压增加量为33%。总体而言，在波浪作用的前30个周期管周孔压增加较快，之后随着波浪作用时间的增加，海床累积孔压的发展速度有所减缓，这从图 6 中累积孔压随时间的发展变化曲线中也可以看出。

图 9 累积孔压沿管土交界面分布对比图Fig. 9 Comparison of residual pore pressures along the interface of pipeline and soils

3.2.2 海床累积孔压发展机制

由前述分析可知，当考虑累积孔压与海床应力的耦合效应时，管线周围和远端海床的累积孔压发展速度均有所增大，尤其是管线附近区域，累积孔压的增大较为显著。根据Liu et al. (2019)的分析可知，在耦合模型下，水平方向累积孔压的不均匀分布会导致海床循环剪应力的不断增加，从而会在较大程度上促进累积孔压的快速发展。如前述图 7 所示，在管线周围海床的累积孔压沿水平方向的差异相对较大，这会导致该区域剪应力的增加，如图 10 所示，可以看出，随着波浪作用周期的增加，管线周围的海床剪应变(剪应力)也有所增大，而剪应变的增大会明显促进累积孔压的发展，因此，在管线附近区域海床的累积孔压相较于远端海床有明显的增大。当不考虑累积孔压与海床应力的耦合效应时，海床剪应力因不受累积孔压的影响而保持不变，因此其累积孔压的发展相对较慢，且管线对海床累积响应的影响范围也相对较小。综上所述，对于管线附近区域的海床，累积孔压沿水平方向分布不均匀而导致的循环剪应力的增大，是耦合模型相对于非耦合模型累积孔压明显增大的主要原因。

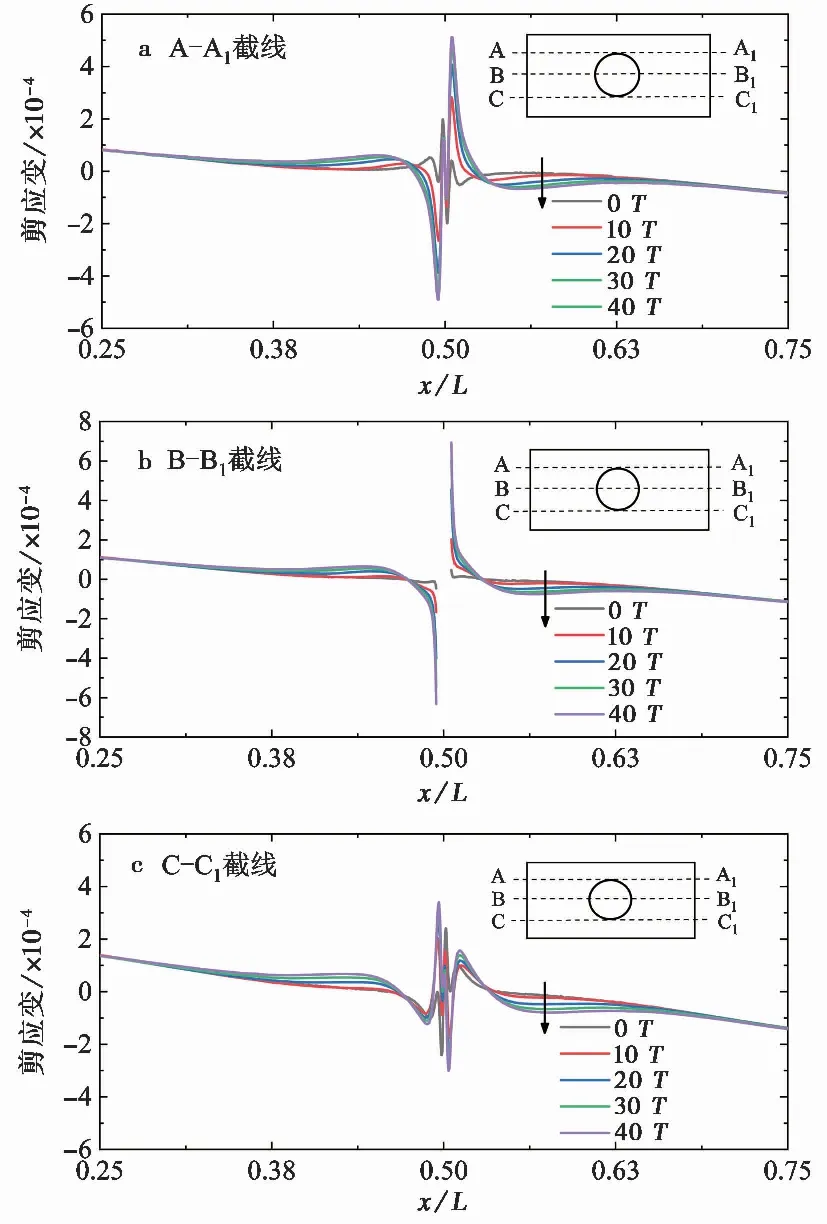
图 10 海床剪应变水平分布图Fig. 10 Lateral distribution of soil shear strain

对于远离管线的区域，管线对累积孔压的影响可以忽略，这些区域的累积孔压在水平方向上分布均匀，因而剪应力不随波浪作用时间而变化； 这些区域内耦合模型计算的海床累积孔压大于非耦合模型计算得到的累积孔压，其根本原因在于累积孔压竖向分布的不均匀而导致的海床平均有效正应力的差异(Liu et al.，2019)，不同深度处耦合模型和非耦合模型平均有效正应力的差异曲线如图 11 所示，深度越大，平均有效正应力的差异就越大，因而两种模型计算所得到的累积孔压的差异也就越大。

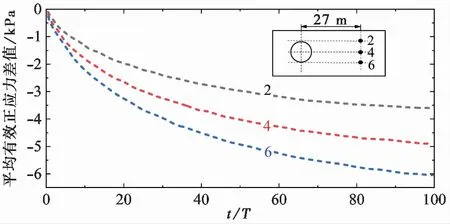
图 11 远点处海床平均有效正应力差值Fig. 11 Difference of the mean effective stress in the far field

3.3 含埋置管线海床渐进液化特征

当海床某深度位置的超静孔隙水压力大于其初始竖向有效应力时，该深度位置的土体会发生液化(Okusa， 1985)，液化准则的表达式为(有效应力以拉为正)：

pres+σ′z0>0

(16)

基于上述液化准则，对不同波浪作用时间下的海床液化区进行分析，结果如图 12 所示。耦合模型下管线周围海床的液化深度相对较大，随着波浪作用时间的增加，液化区在竖向自上而下不断发展，水平方向上液化区从管线附近逐渐向两侧不断扩展，至20T时，管线顶部周围海床发生液化； 至60T时，管线底部附近的海床开始液化，此时管线周围海床的最大液化深度约为3.5 m。而对于非耦合模型，由于累积孔压发展相对较慢，相应波浪作用时间海床尚未液化。因此，当不考虑累积孔压与海床应力的耦合效应时，可能会一定程度地低估管线周围海床的液化深度，不利于管线的安全设计。

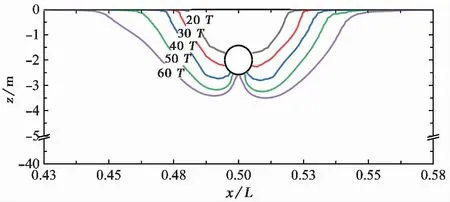
图 12 管线埋深2 m时海床的液化区分布图Fig. 12 Liquefaction zone of the seabed around the pipeline at a buried depth of 2 m

管线的埋深对其周围海床累积孔压的发展和液化具有重要影响(Zhao et al.，2014)，一般而言，管线埋置深度越深，其周围海床液化发展速度越慢。如图 13 所示，为管线埋置深度为3 m时不同波浪作用时间下海床的液化区分布，在20T时，液化深度尚未达到管线顶端，而在60T时，管线底部区域的海床也尚未全部液化，与管线埋置深度为2 m时的液化区分布图对比可知，管线埋置深度越深，越有利于管线的安全。

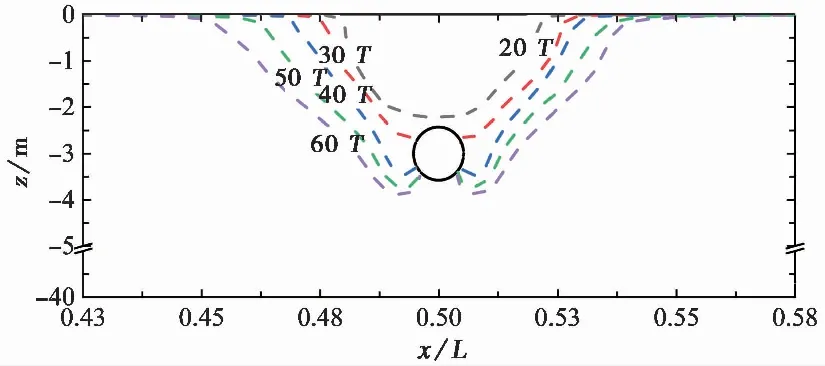
图 13 管线埋深为3 m时海床的液化区分布图Fig. 13 Liquefaction zone of the seabed around the pipeline at a buried depth of 3 m

需要注意的是，上述分析是基于渗透系数较小的相对松散的深厚均质粉砂或细砂层地基，且波浪条件相对极端情况下的计算结果，由于海床渗透系数较小且相对松散，孔压极易累积，因此，液化深度相对较大。在实际工程中，宜充分考虑管线周围海床的实际地层条件，准确确定计算参数，在保证管线安全的前提下避免设计过度保守。

4 结 论

对非线性行进波作用下含埋置管线海床的累积响应特征和液化进行了数值模拟分析，探讨了孔压累积与海床应力耦合效应下管线周围海床累积响应特征及其发展机制，并与不考虑孔压累积与海床应力耦合效应的结果进行了对比分析，主要得到以下结论：

(1)行进波作用下，埋置管线附近海床的累积孔压发展相对较快，其中管周下半部分海床的累积孔压发展速度较其上半部分发展更快，尤以管线底端点的累积孔压发展最为显著。

(2)孔压累积与海床应力的耦合效应会显著增大管线对其周围海床累积孔压特征的影响，这种影响一方面体现在管线周围海床累积孔压的更快发展，另一方面体现在管线对孔压影响范围的扩大。结果分析表明，考虑累积孔压与应力的耦合效应时，管线的影响范围随波浪作用时间会有所增大； 当忽略累积孔压与应力的耦合效应时，管线的影响范围基本不随波浪作用时间而变化。

(3)由于累积孔压与应力的耦合效应，管线附近累积孔压的不均匀分布会引起海床循环剪应力的增大，从而导致管线周围海床累积孔隙水压力的快速发展，并促进海床的液化，忽略这种耦合效应会在一定程度上低估海床液化深度，不利于管线安全。实际工程设计中，应充分考虑管线周围海床的实际地层条件，合理确定计算参数，保证管线的安全。