0–1 膨胀几何分布的客观贝叶斯分析
肖 翔,古 晞
(1.上海工程技术大学 数理与统计学院,上海 201620;2.同济大学 数学科学学院,上海 200092)
在医疗卫生、保险金融及可靠性等许多实际应用领域,样本数据不仅会出现零过多的情况,也会出现一过多的情况.例如,在新型冠状病毒(COVID–19)大流行时,个体感染COVID–19 后,自身就会产生抗体,使其感染次数最多可能一次.又如,在商场买衣服时,出于货比三家的心理,很多顾客没有购买衣服或者只购买一件衣服.
近年来,国内外很多文献对0–1 膨胀泊松分布模型进行了深入研究,取得丰富的研究成果.田震[1]基于数据删失和加权扰动模型对0–1 膨胀泊松分布模型进行统计推断.Tang 等[2]构造0–1 膨胀泊松分布模型的等价表达式,采用极大似然估计与贝叶斯方法对新加坡军团菌感染病例数据进行研究.Liu 等[3]利用广义最大期望(EM)算法对0–1 膨胀泊松分布回归模型中的参数进行估计,对美国底特律城市交通事故死亡数据进行拟合.夏丽丽等[4]使用局部多项式核回归法对0–1 膨胀泊松分布模型进行参数估计,通过对北京市糖尿病患者数据的分析,验证了局部多项式核回归方法的有效性.
对于0–1 膨胀泊松分布模型,当数据存在较大变异时,即样本均值与样本方差不相等时,如果仍然用模型进行拟合,效果往往不好.而0–1 膨胀几何分布模型,不仅可以用于处理样本数据的变异,也适应于样本尾部数据退化较慢的情形.对于0–1 膨胀几何分布及其回归模型,目前研究文献较少,肖翔[5]利用贝叶斯方法对0–1 膨胀几何分布回归模型进行参数估计,Xiao 等[6]基于Polya-Gamma 潜变量设计0–1膨胀几何分布回归模型中后验样本的抽样机制.本研究对0–1 膨胀几何分布模型进行参数变换,计算出客观贝叶斯先验,以期得到更好的拟合效果.
1 0–1 膨胀几何分布模型
本研究提出0–1 膨胀几何分布(简称为ZOIGE)模型,即一个非负的0-1 膨胀几何分布的随机变量Y,可以表示为Y=V(1−B1)+B1(1−B2).其 中,B1、B2、V相互独立,B1为一个试验成功概率为p1的伯努利随机变量;B2为一个试验成功概率为p2的伯努利随机变量;V为一个服从于试验成功概率为 θ的几何分布随机变量,即P(V=k)=θk(1−θ),k=0,1,···.随机变量Y的分布律为
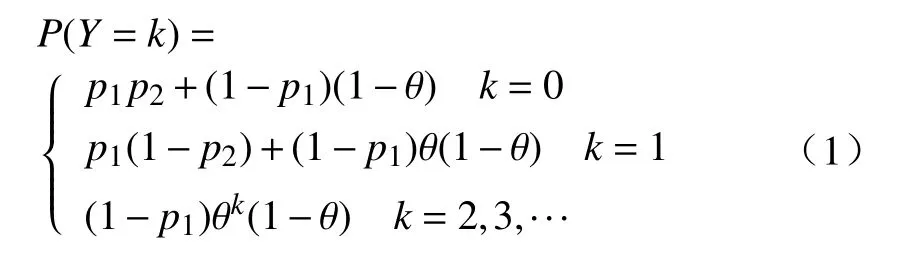
式中:0 ≤p1≤1,0 ≤p2≤1,0 ≤θ ≤1.可以看出,0–1 膨胀几何分布是由伯努利分布与几何分布按照比例p1和1−p1组成的混合分布.当p2=1时,ZOIGE变成零膨胀几何分布(ZIGE)[7−8],当p1=0时,ZOIGE 退化成几何分布.
进行参数变换,令
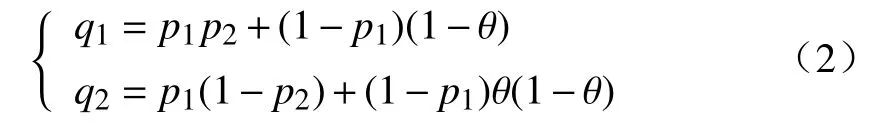
可得

通过上述重参数化,式(1)变为
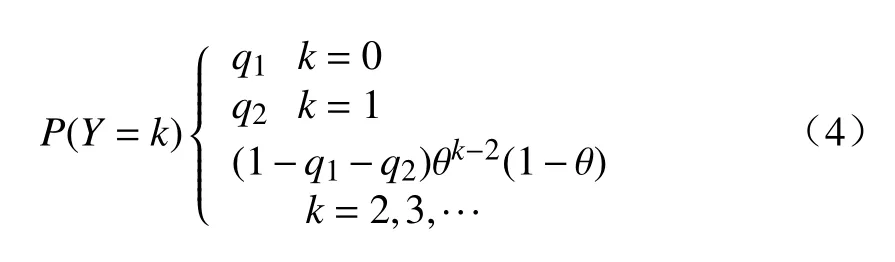
式中:q1≥0,q2≥0,q1+q2≤1,0 ≤θ ≤1.
设Y=(Y1,Y2,···,Yn)为取自0–1 膨胀几何分布的观测值,由式(4)得出似然函数公式为
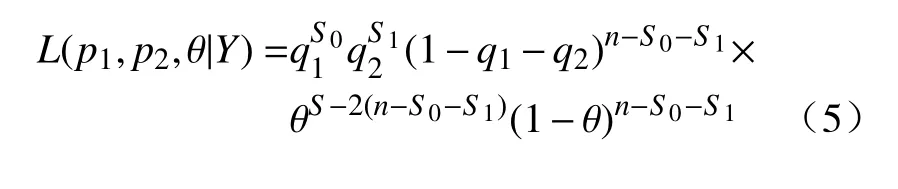
式中:S0=#{i:Yi=0}为集合{i:Yi=0}中包含元素的个数;为集合{i:Yi=1}中包含元素的个数;
式(5)两边取对数,得到对数似然函数为
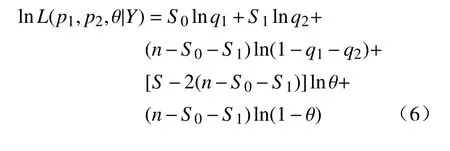
2 客观先验
2.1 Fisher 信息矩阵
计算随机变量Y,S0,S1,S的期望为
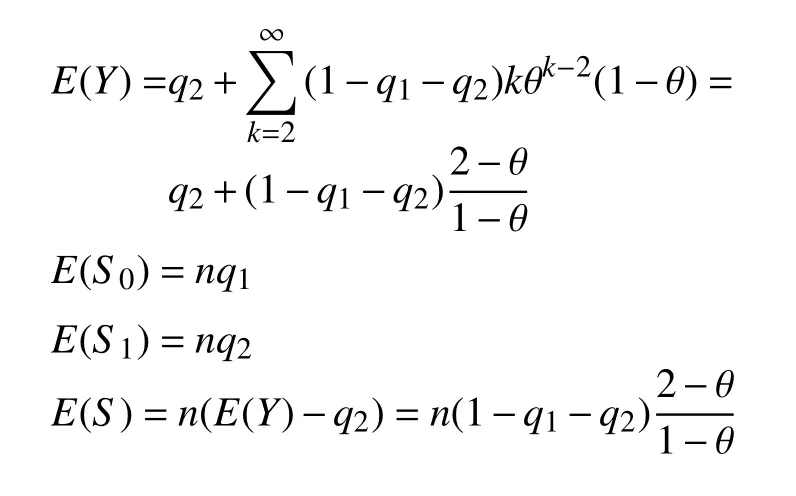
计算对数似然函数式(6)的一阶偏导数为
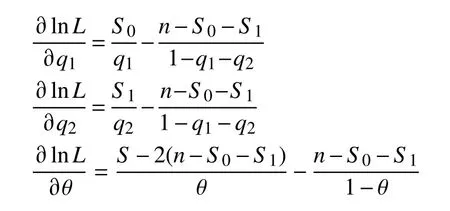
计算对数似然函数式(6)的二阶偏导数为
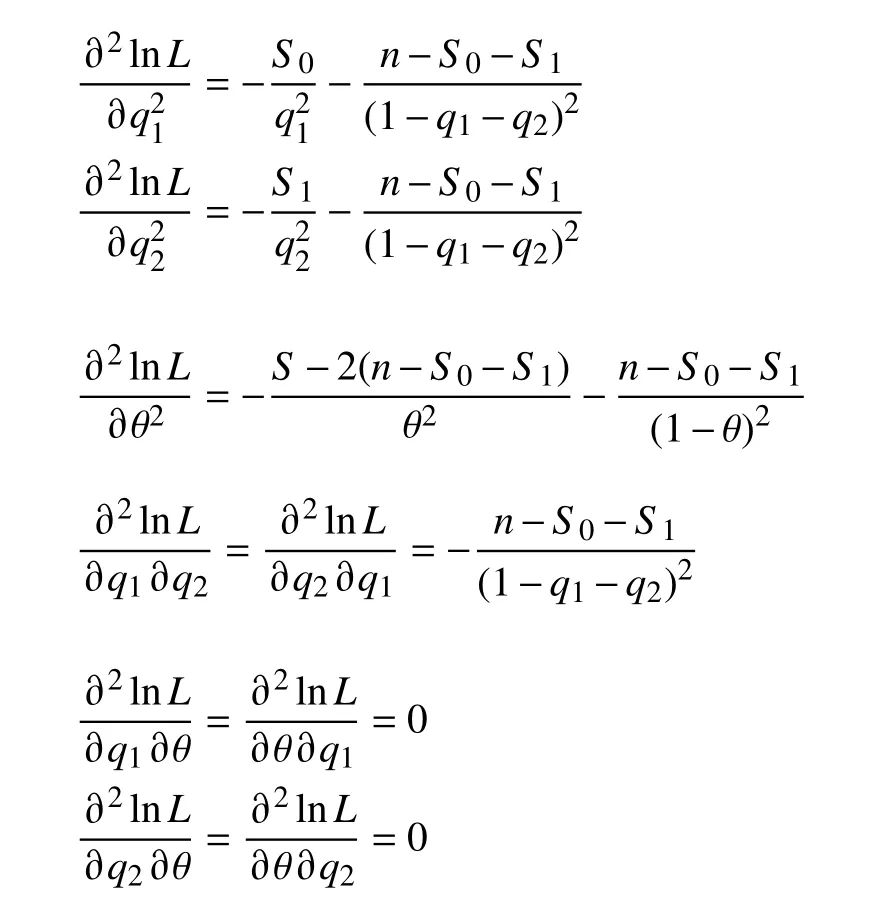
进一步计算二阶偏导数期望的相反数,它们是Fisher 信息阵的组成元素.表达式为
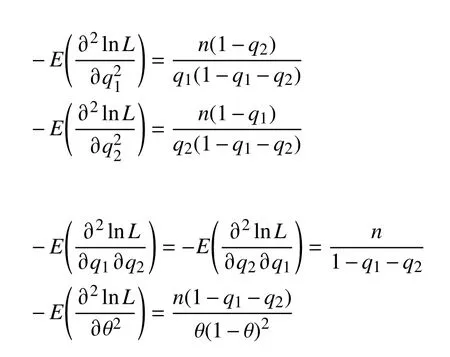
因此,(q1,q2,θ)的Fisher 信息阵为
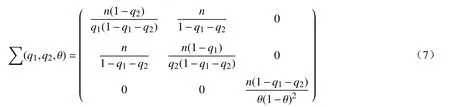
2.2 Jeffreys 先验
与Laplace 先验比较,Jeffreys 先验能够在参数变换下保持不变性,比Laplace 先验具有更广泛的应用场合[9].参数(q1,q2,θ)的Jeffreys 先验与Fisher信息矩阵行列式的平方根成正比,通过式(7)可以计算(q1,q2,θ)的Jeffreys 先验,公式为
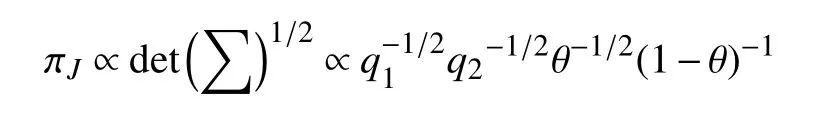
2.3 Reference 先验
对于参数组合{(∑q1,q2),θ},(q1,q2)为感兴趣的参数,Fisher 信息矩阵(q1,q2,θ)可写成
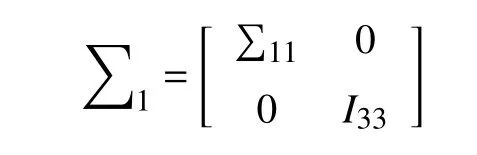
其中
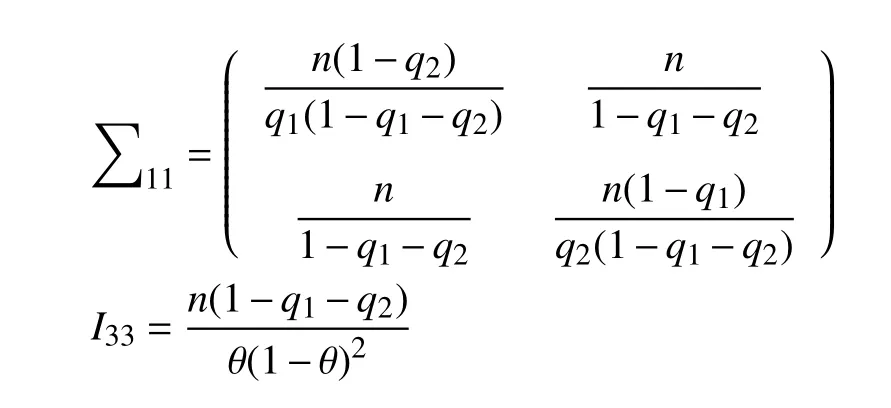
根据文献[10],reference 先验求解过程中,先求出h1和h2,公式为
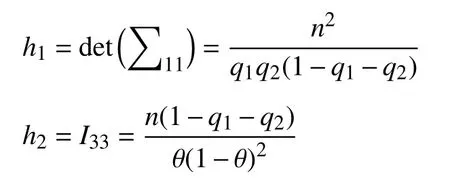
再完成以下4 个步骤.
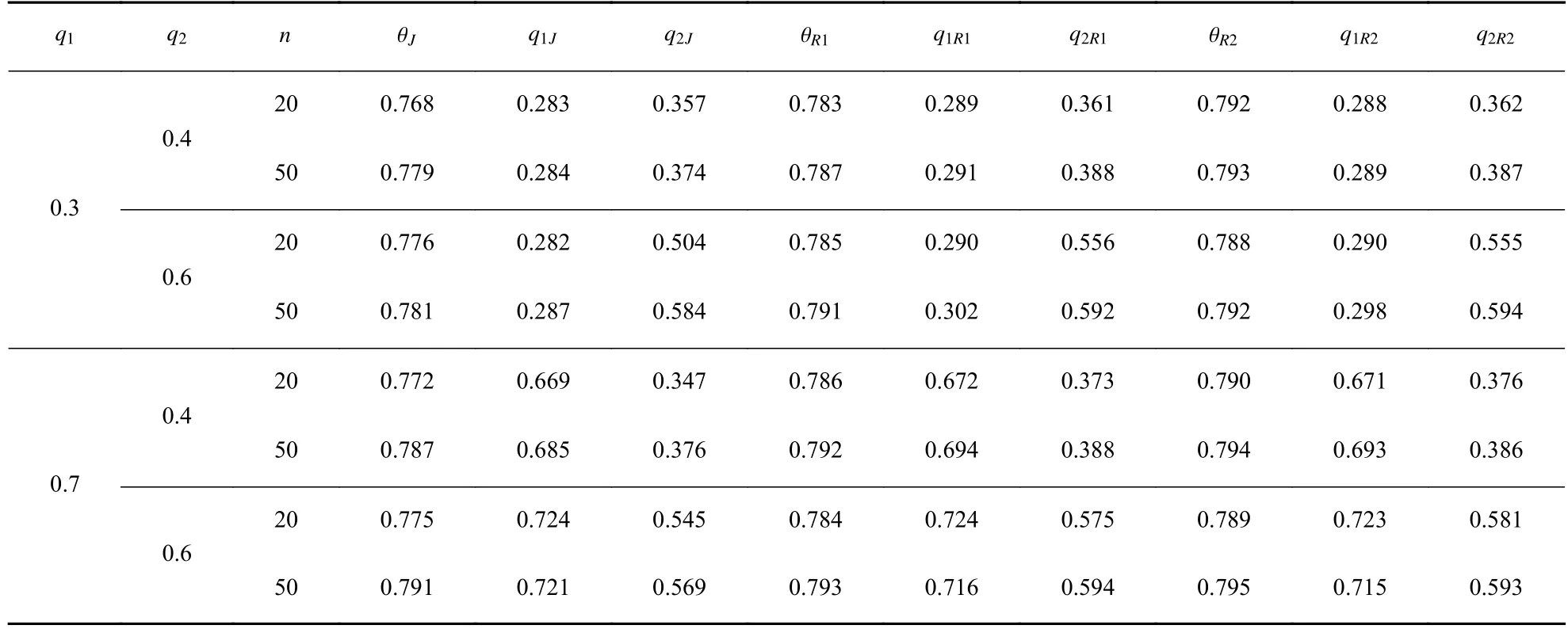
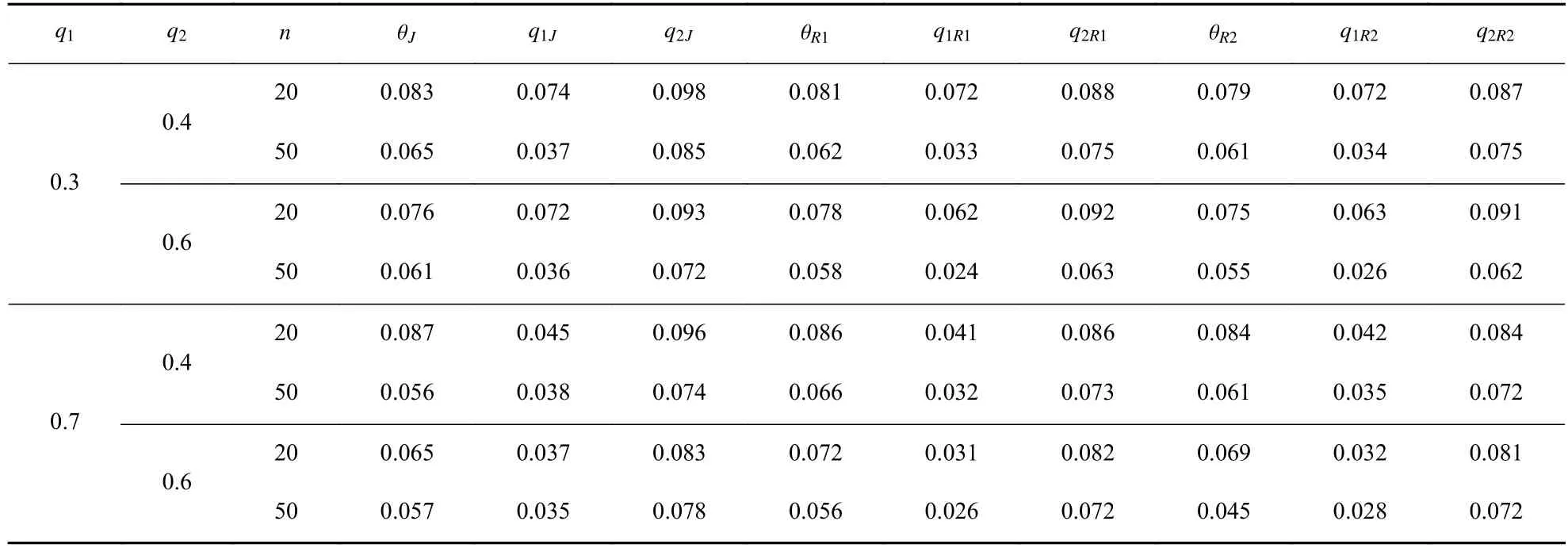
步骤1选取参数空间的一组紧子集为Ωi=Ω12×Ω3i={(q1,q2)|0 步骤2当(q1,q2)给定时,θ的条件先验为 步骤3结合式(8),(q1,q2)的边缘先验为 步骤4Φ的reference 先验为 对于参数组∑合{θ,(q1,q2)},θ为感兴趣的参数,Fisher 信息矩阵(q1,q2,θ)可写成 步骤1选取与{(q1,q2),θ}参数空间中相同的一组紧子集. 步骤2当 θ给定时,结合式(8),(q1,q2)的条件先验为 步骤3结合式(8),θ的边缘先验为 步骤4Φ的reference 先验为 基于先验分布 πJ,πR1和πR2,分别得到它们的后验分布,通过R 软件进行抽样,获取后验样本.以πR1为例,(q1,q2,θ)的后验分布为 式中:Y=(Y1,Y2,···,Yn)为观测数据.式(9)的具体形式为 从式(10)可以看出,(q1,q2)的后验边缘分布为 本节基于Jeffreys 先验和reference 先验,通过数值模拟对ZOIGE 模型的参数进行估计.样本容量分别设为n=20和n=50,θ值设为 0.8,q1的值分别设为 0.3和0.7,q2值分别设为 0.4和 0.6,所有模拟重复2 000 次,计算出参数估计量的均值和均方误差见表1 和表2.从表中可以看出,随着样本容量的增加,3 种客观贝叶斯先验下的估计值越来越接近真值,均方误差也越来越小.对于q1和q2的估计,πR1、πR2比 πJ表现更好,这是因为在πR1、πR2中包含q1和q2的信息更加丰富.对于 θ的估计,πR2比πR1、πJ表现更好,这是因为在πR2中 θ为感兴趣参数,集中了更多的样本信息. 表1 θ=0.8下参数估计量的均值Table 1 Mean of parameter estimators whenθ=0.8 表2 θ=0.8下参数估计量的均方误差Table 2 Mean squared error of parameter estimators whenθ=0.8 本研究对0–1 膨胀几何分布模型进行客观贝叶斯分析,巧妙地进行重参数化,写出具有分块对角形式的Fisher 信息矩阵.因而,较容易推导出参数的Jeffreys 先验和reference 先验,这种方法和技巧可以推广到其他形式的0–1 膨胀分布模型中去.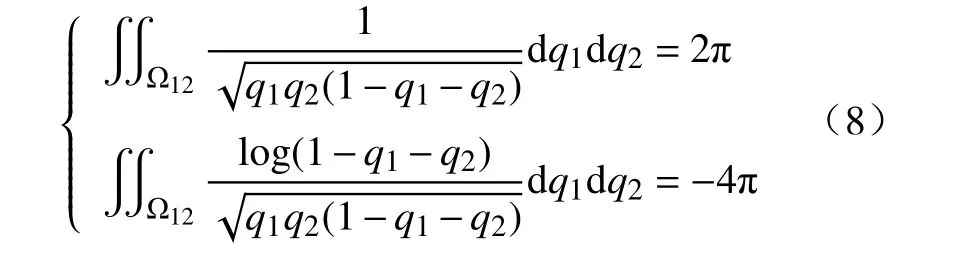
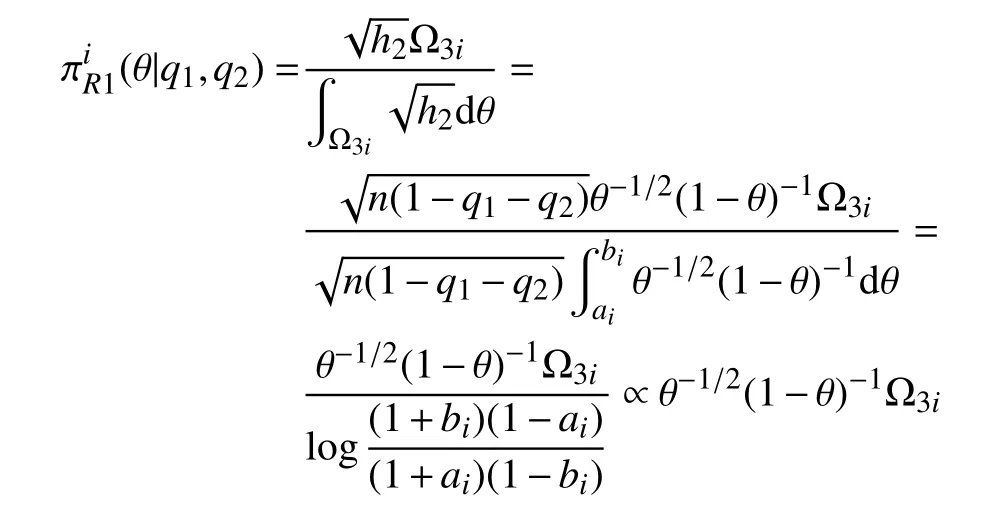
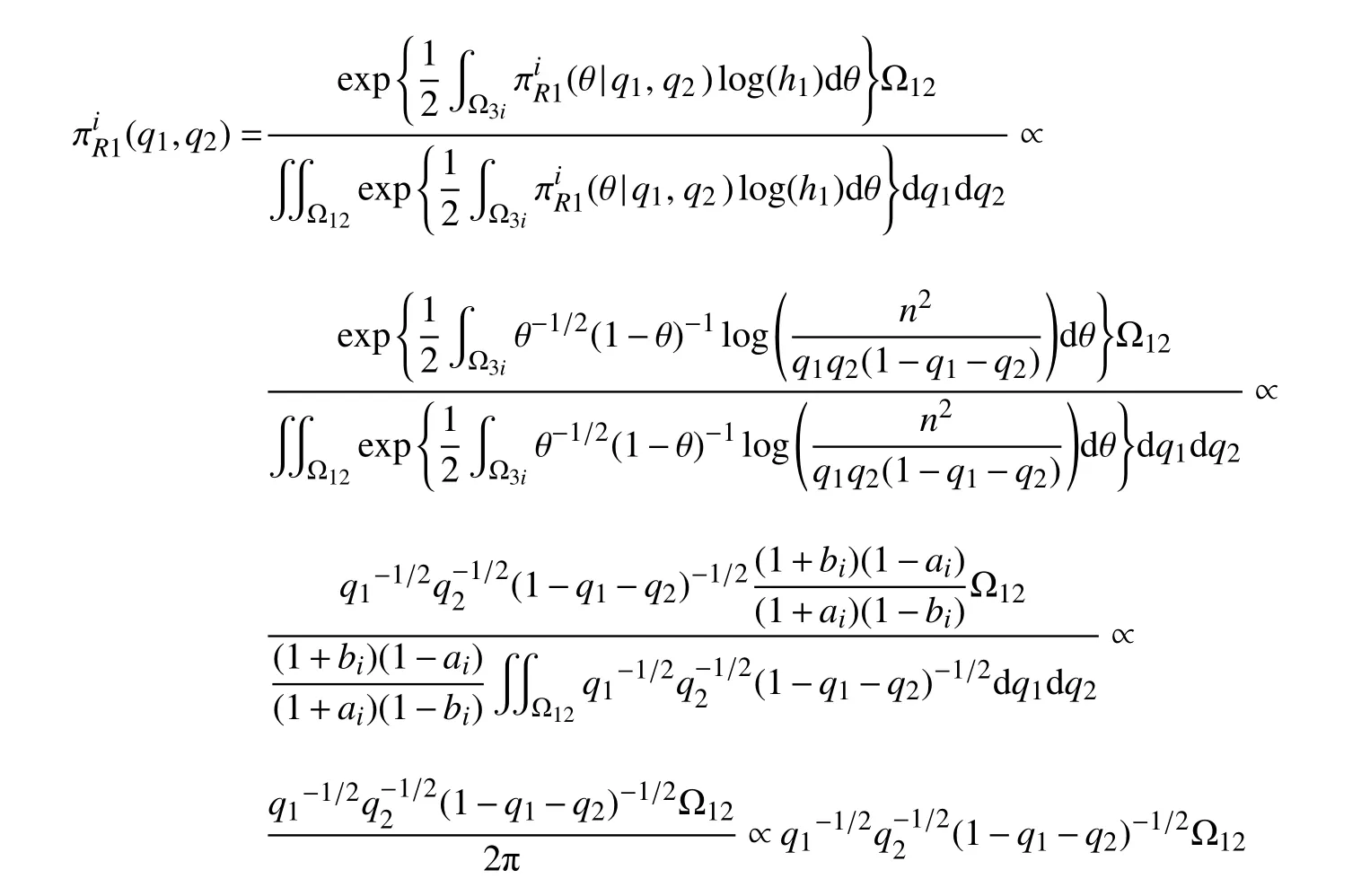
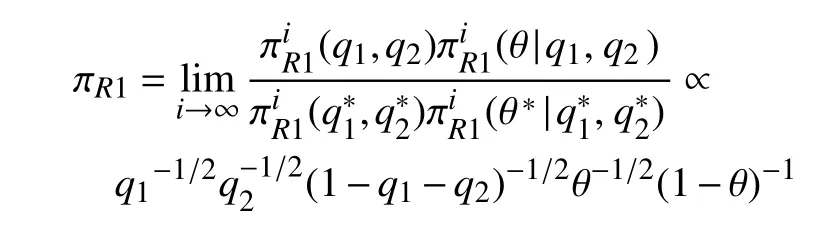
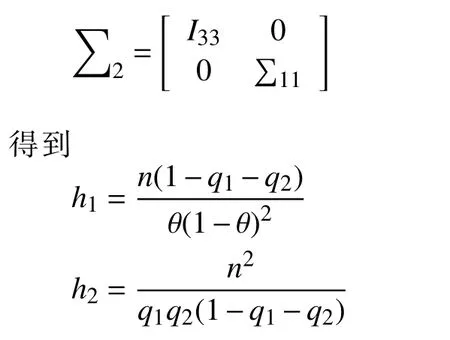
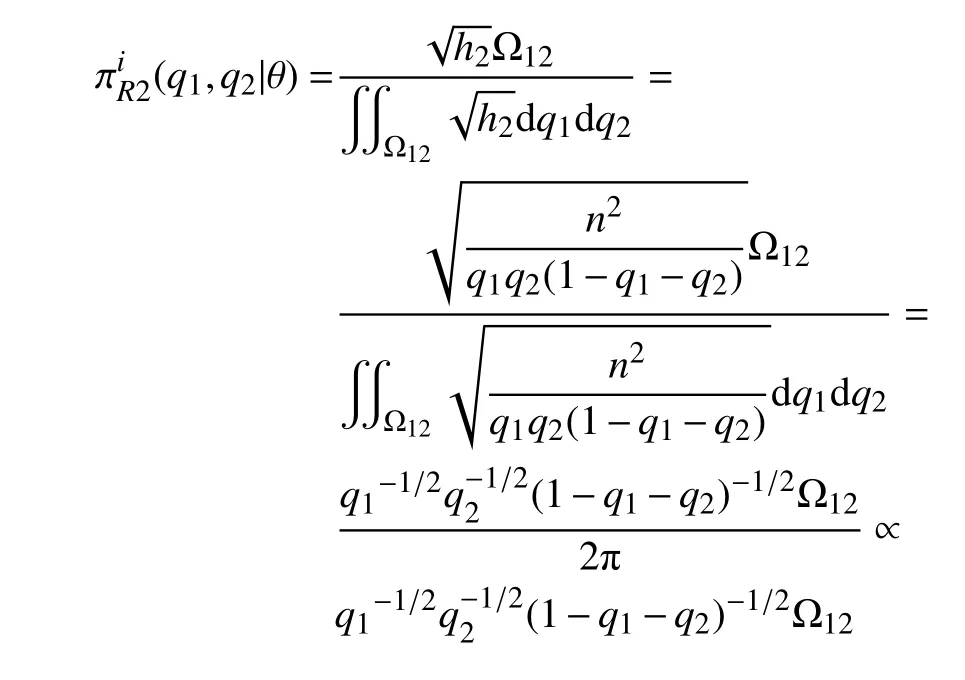
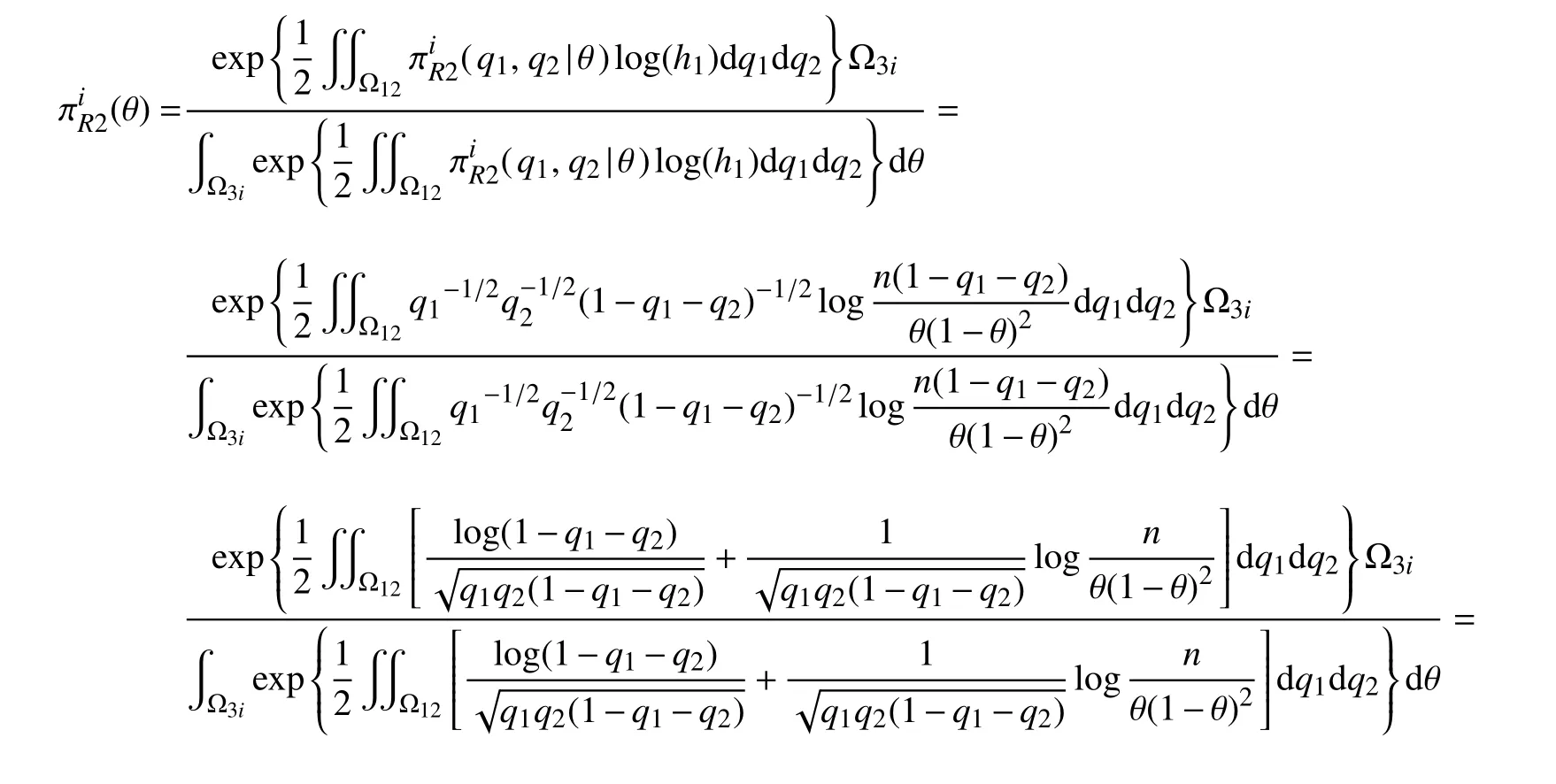

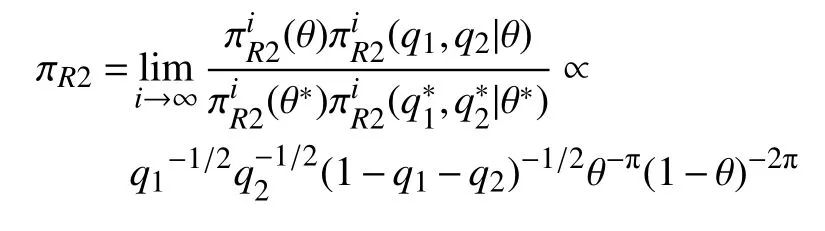
3 后验分析
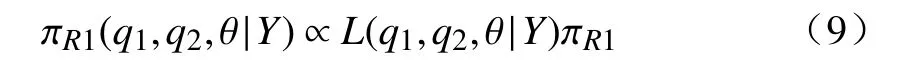

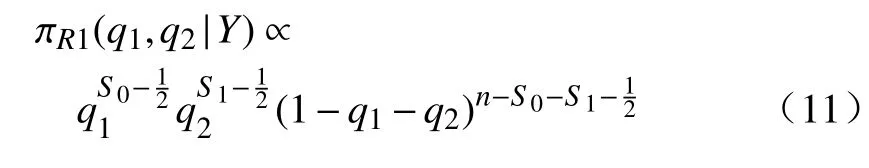
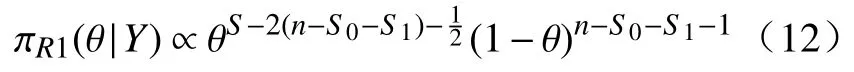
4 数值模拟
5 结语

