基于奇异值分解的改进TCKF姿态估计算法*

钱镭源, 张建强，许国强, 曹文涛

(1.运城职业技术大学 智能制造与数智矿山学院，山西 运城 044000；2.阳煤丰喜肥业(集团)有限责任公司，山西 运城 044000)

微电机系统(Micro-Electro-Mechanical Systems，MEMS)在惯性器件上的应用推动了捷联惯性导航系统(Strapdown Inertial Navigation System，SINS)的发展[1]，使SINS被广泛用于煤矿、水下勘探等场合[2-3]。但MEMS-SINS本身受加速度计、陀螺仪和磁力计等惯性器件自身特性的影响[4]，无法对姿态角信息进行精确解算[5]。针对这一问题，科研人员进行了诸多相关研究，GENG Jijun等人提出了一种基于四元数解算的自适应容积卡尔曼滤波(Adaptive Cubature Kalman Filter，ACKF)算法[6]，有效提高了姿态角的估计精度；Chiella Antonio C B等人提出了一种基于四元数的鲁棒自适应无迹卡尔曼滤波(Quaternion Robust Adaptive Unscented Kalman Filter，QRAUKF)算法，解决了MEMS传感器姿态精度下降的问题[7]。

实际应用中，滤波算法常会出现误差协方差矩阵非正定导致运行终止的问题，平方根滤波和奇异值分解是解决这一问题最常用的方法[8-10]。但平方根滤波在每次循环运算时，均进行三角分解，造成算法误差积累；而奇异值分解能够将复杂矩阵以特征值与特征向量乘积的形式表示，避免开方运算，具有更高的鲁棒性[11]。2018年，秦康等人为了解决CKF的非局部采样问题，对采样点进行正交变换，提出了一种滤波性能优于CKF的正交变换容积卡尔曼滤波(Transformed Cubature Kalman Filter，TCKF)方法[12]。

为提高TCKF算法的滤波精度和姿态测量系统的性能，本文将奇异值分解引入到TCKF算法中，将其应用于九轴姿态测量系统，提出了基于奇异值分解的改进TCKF姿态估计算法。该算法在对姿态数据进行融合的同时，对TCKF的误差协方差矩阵进行SVD分解，代替原有的Cholesky分解，保证融合过程中协方差矩阵始终正定，提高姿态估计的稳定性和精度。

1 数据融合方案及数学模型

1.1 数据融合方案

为了保证系统输出持续可靠的姿态信息，本文设计了一种基于奇异值分解的改进TCKF姿态数据融合方案，如图1所示。该方案以捷联姿态解算得到的姿态四元数作为系统状态，以加速度计计算的俯仰角和横滚角、磁力计计算的航向角作为系统量测，采用ASVDTCKF算法对测量数据进行融合，估计姿态四元数，进而得到准确的姿态角信息。其中，姿态四元数的初值由加速度计和磁力计的测量数据计算得到。

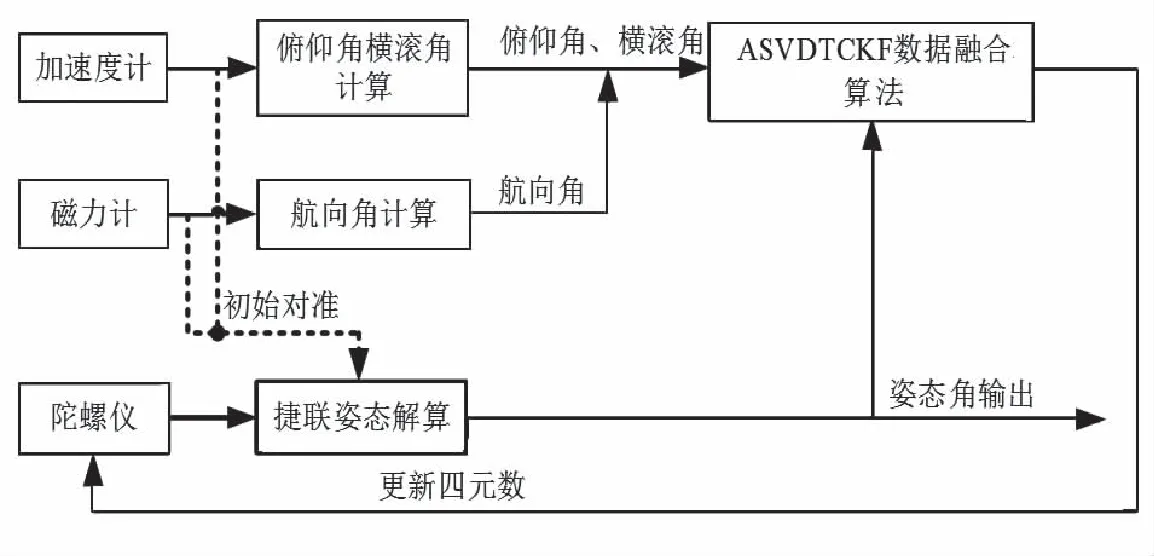
图1 姿态数据融合方案

1.2 姿态测量系统数学模型

由图1可知，姿态测量系统的数学模型可简化为：

(1)

式中，xk为k时刻的状态向量，即姿态四元数；f(·)为系统k-1时刻到k时刻的状态转移矩阵；wk-1为k-1时刻的过程噪声，其协方差矩阵为Qk-1；zk为系统k时刻的量测向量；h(·)为k时刻的量测矩阵；vk为系统k时刻的量测噪声，其协方差矩阵为Rk。

采用捷联姿态解算得到的姿态四元数作为系统状态量，即：

xk=[q0q1q2q3]

(2)

式中，q0、q1、q2和q3为姿态四元数，其运动学微分方程为：

(3)

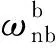
根据四阶角增量法，系统的状态转移矩阵为：

(4)

系统量测为：

z=[θaccφaccΨ]

(5)

式中，θacc和φacc分别由以下公式计算得到：

(6)

其中，ax、ay和az分别为载体水平或匀速时三轴加速度计的测量结果。

Ψ由以下公式计算得到：

Ψ=Ψm+λ

(7)

式中，Ψm为磁航向角；λ为载体真实航向角与磁航向角之间存在的磁偏角。

根据量测值θacc、φacc、Ψ与状态向量

[q0q1q2q3]之间的关系[13]，系统量测矩阵为：

(8)

2 ASVDTCKF算法设计

2.1 TCKF算法流程

(1)根据三阶球面-径向容积准则，计算CKF的采样点ξj和权值ωj：

(9)

式中，n为系统状态向量维数；j=1,2,…,2n；[1]2n为2n维单位球面与各坐标轴的交点，

则采样点集可进一步表示成：

(11)

(2)对CKF采样点ξj进行正交变换，得到TCKF的采样点λj，即[12]：

Bξ=[λ1|λ2|…|λ2n]

(12)

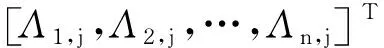
(13)

(14)

(15)

式中，r=1,2,…,n/2，当n为奇数时，Λn,j=(-1)j。

(3)基于状态估计的采样点计算：

(16)

(17)

(4)状态预测：

(18)

式中，L=2n。

(5)计算状态预测误差的协方差矩阵：

(19)

(6)计算基于状态预测的采样点：

(20)

(21)

(7)量测预测：

(22)

(8)计算新息的协方差矩阵：

(23)

(9)计算状态向量与量测向量之间的互协方差矩阵：

(24)

(10)计算卡尔曼滤波增益：

(25)

(11)状态估计：

(26)

(12)更新协方差矩阵：

(27)

2.2 基于奇异值分解的滤波方程推导

SVD分解的基本原理如下[14]：

设A是一个m×n维的实数阵，对其进行SVD分解：

(28)

式中，U和V均为酉矩阵；M=diag(σ1,σ2,…，σr)为奇异值矩阵；r为M的秩。

本文将SVD分解引入到TCKF算法中，代替原有的Cholesky分解，提高TCKF算法的稳定性。具体改进如下：

(29)

(30)

(31)

(32)

将奇异值分解滤波方程和TCKF引入图1姿态测量系统中，即可得到基于奇异值分解的改进TCKF姿态估计算法ASVDTCKF。

3 实验方案

本文采用ADI公司的ADIS16405微惯性测量单元和TI公司的OMAP-L138构建了姿态测量硬件系统，如图2所示。第一层为ADIS16405模块和变压器模块，用于降压和提供三轴加速度计、三轴陀螺仪、三轴磁力计的原始测量数据；第二层为OMAP-L138双核微处理器及其核心板，用于解析ADIS16405提供的原始数据、时间对准和数据传输；第三层为电源模块，为整个系统供电；第四层为功能拓展层。

图2 姿态测量硬件系统图

为了分析ASVDTCKF算法的性能，本文将姿态测量硬件系统固定于转台，分别进行静态和三轴摇摆实验，并将OMAP-L138采集的惯性数据保存于第三层的U盘中，接入PC机，在MATLAB中进行姿态数据融合算法性能对比实验，实验系统安装如图3所示。

图3 实验系统安装图

4 实验结果分析

4.1 静态实验

设置转台处于静止状态，启动姿态测量系统，持续30 s，数据采集的频率为100 Hz。分别采用基于TCKF的姿态估计算法(ATCKF)、基于平方根滤波的TCKF姿态估计算法(ASRTCKF)和ASVDTCKF进行数据融合。

静态环境下不同算法的运行情况如表1所示，算法输出的姿态角如图4所示，角度均方根误差(RMSE)如表2所示，算法运行时间如表3所示。由表1可知，ASRTCKF和ASVDTCKF运行正常，而ATCKF因协方差矩阵非正定而异常终止，说明对协方差矩阵进行QR分解或SVD分解能够提升算法的稳定性。由图4和表2可知，静态条件下ASVDTCKF输出的俯仰角误差、横滚角误差和航向角误差与ASRTCKF相比分别减小了20.6%、2.9%和4.6%，说明ASVDTCKF与ASRTCKF相比具有更高的姿态估计精度。由表3可知，ASVDTCKF的运行时间与ASRTCKF相比减少了18.9%，说明SVD分解的运算量低于QR分解。

表1 静态条件下不同算法运行情况比较

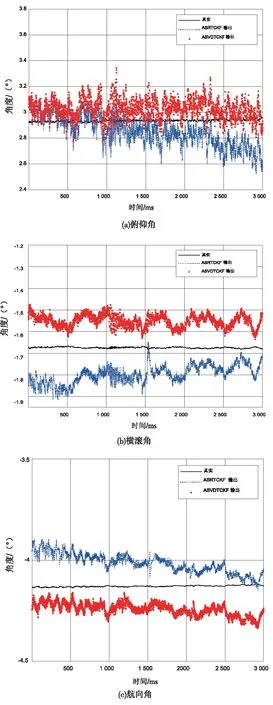
图4 静态环境下不同算法输出的姿态角

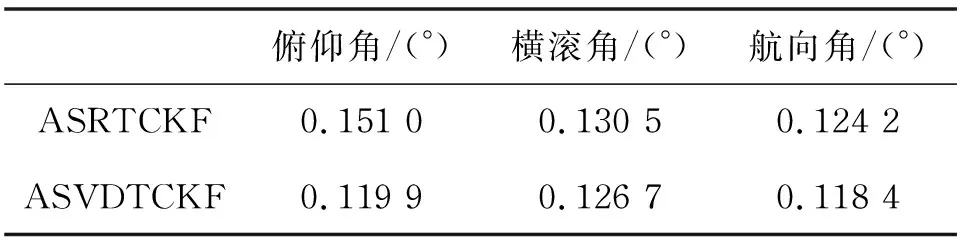
表2 静态条件下不同算法的RMSE

表3 静态条件下不同算法运算时间

4.2 动态实验

设置转台处于摇摆状态，持续30 s，摇摆幅度为20°，摇摆频率为0.5 Hz，数据采集频率为100 Hz。分别采用ATCKF、ASRTCKF和ASVDTCKF对摇摆状态下的ADIS16405测量数据进行融合。

摇摆状态下不同算法运行情况如表4所示，不同算法输出的姿态角结果如图5所示，角度RMSE如表5所示，算法运行时间如表6所示。由表4可知，摇摆动态环境下，ASRTCKF和ASVDTCKF运行正常，ATCKF算法运行至1步终止，说明动态条件下QR分解或SVD分解能够使算法运行稳定。由图5和表5可知，动态条件下ASVDTCKF算法的估计精度更优，与ASRTCKF相比，俯仰角误差、横滚角误差和航向角误差分别减小了0.89%、27.5%和7.4%。由表6可知，动态条件下ASVDTCKF的运算时间与ASRTCKF相比减少了20.5%，说明ASVDTCKF算法的运算效率更高。

表4 摇摆环境下不同算法运行情况比较

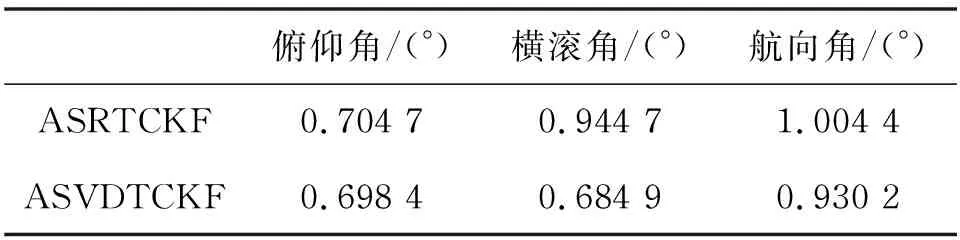
表5 摇摆条件下不同算法的RMSE

表6 摇摆条件下不同算法运算时间

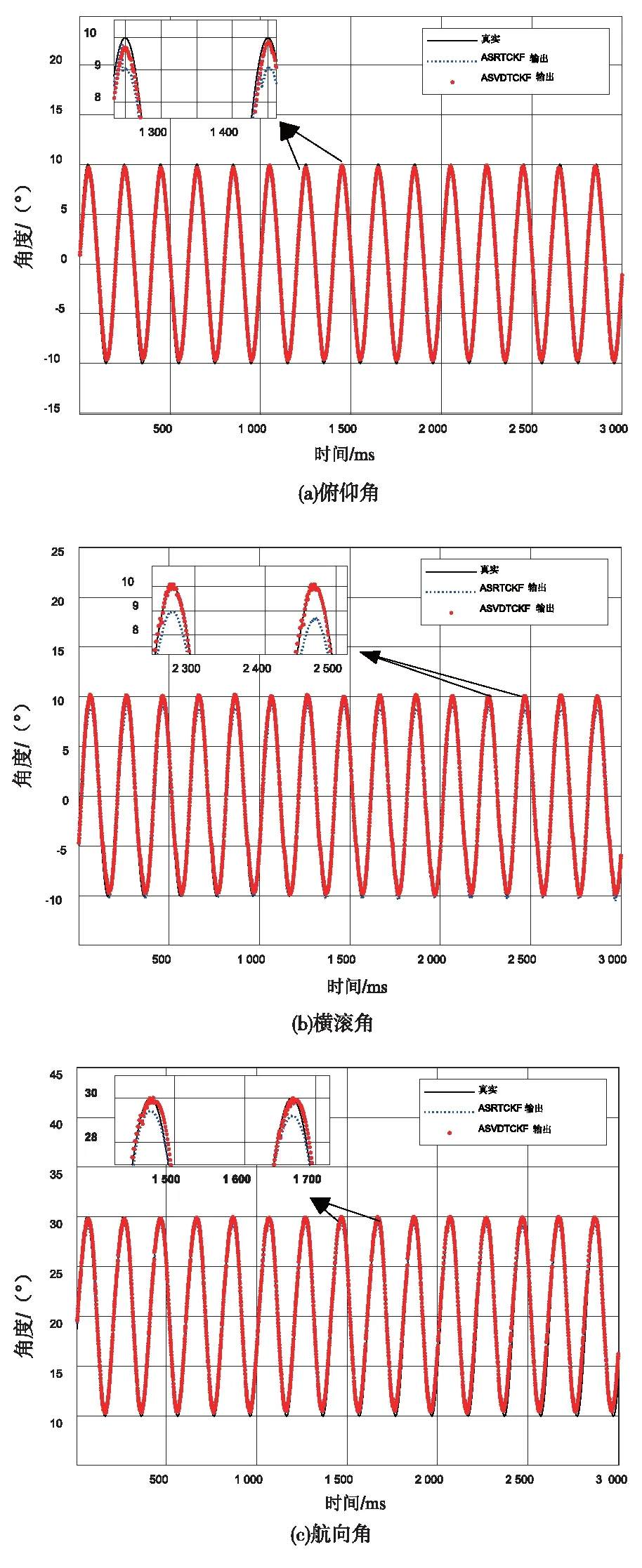
图5 摇摆环境下不同算法输出的姿态角

5 结 论

为了提高TCKF算法的滤波稳定性及MEMS器件的姿态解算精度，本文提出了一种基于奇异值分解的改进TCKF姿态估计算法。该算法对MEMS器件输出的姿态数据进行融合，对误差协方差矩阵进行奇异值分解，提高了姿态角信息的测量效果。将ADIS16405姿态测量硬件系统固定于转台，以静态和三轴摇摆时系统输出的原始九轴数据作为实验数据。实验结果表明：(1)基于奇异值分解的改进TCKF姿态估计算法与ASRTCKF在实际姿态测量中均能保证误差协方差矩阵始终正定，与TCKF相比，具有更强的运行稳定性；(2)基于奇异值分解的改进TCKF姿态估计算法仅对误差协方差矩阵进行一次奇异值分解运算，与进行平方根运算的ASRTCKF相比，解决了平方根三角分解造成的误差积累问题，具有更高滤波精度和运算效率。因此，该算法在矿山、水中、隧道等复杂情况下的载体姿态测量中具有较强的硬件实现性和适用性。