振动信号Fourier分析下高耸结构损伤识别仿真

徐兆赫，徐 亮

(北京科技大学天津学院，天津 301830)

1 引言

高耸的建筑结构在其使用期间受到设计荷载或是其它外界突发因素的影响，其结构会出现不同程度的损伤，进而威胁到高耸建筑的整体结构安全。另外，建筑结构的老化会导致高耸结构强度的减低、刚度的退化，这也可以被当做一种结构损伤。而结构老化会产生大量的维修费，由此可见，因为高耸结构损伤致使的后果会造成巨大的经济损失。这就要需要一种对高耸构架损伤进行有效识别的方法。对此国内外学者提出了一下几种解决方法。

文献[1]首先通过数据驱动随机子空间方法对高耸结构进行处理，进而得到结构的随机状态空间模型，然后利用变换矩阵把空间模型转换成特性形式，再经过矩阵特征值分解特征向量矩阵的构架，并评测高耸结构是否存在损伤或损伤的程度。随后使用矩阵与离散输出矩阵转换矩阵里含有的测点信息，通过信息定位损伤位置，从而完成对高耸结构的损伤识别。但是该方法需要大量的时间来完成每种矩阵的离散转换，这就导致了该方法在整体损伤识别中出现效率过低的问题。文献[2]首先通过正常的高耸结构来划分图提取含有单一结构的局部影响，同时分别凭借高耸结构的形状、边缘与位置来建造能量函数的每种约束项，然后使用最小割算法对能量函数的最小值求解，凭借最大期望算法划分出分类阈值，通过对比阈值来完成对高耸结构损伤的识别。但是该方法只是通过能量函数的最小值来进行求解计算，该方法很可能会出现识别不精准的问题。文献[3]首先使用简单线性迭代聚类对高耸的结构进行超像素划分，并使用梯度与色彩直方图的特征建造视觉词袋模型，最后通过支持向量机对模型进行损坏检测。通过检测的结果对比高耸结构的损坏区域，来识别出结构的损坏位置。但是该方法需要对结构进行超像素划分，而这种划分方法需要消耗大量的人力与时间，导致该方法在识别完成后所需要的时间大大增长。

上述问题中效率低下和识别损伤区域不精准的问题，都会对识别高耸结构损伤造成一些不必要的损失，对比本文提出了一种振动信号Fourier分析下高耸结构结构损伤识别方法，关键点在于引入正交小波分析方法把信号分解为交织在一起的多种尺度成分，不断的聚焦到对应的任意微小细节，利用离散小波构建时间序列模型，对高耸结构损伤状态的传递函数进行优化，能够有效的对高耸结构进行损伤识别。

2 基于振动信号Fourier的高耸结构结构损伤识别

2.1 Fourier的基础理论

Fourier分析的基础是把一种随机的函数f(x)，将其代替一组标准函数{eiwx|w∈R}的加权求和

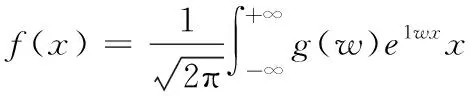
(1)

式中，g(w)为权函数，将初始函数f(x)通过Fourier进行转换，这样就能够把初始函数f(x)的研究转换为对权系数[4]、就是对Fourier转换g(w)的研究。因此，经典的Fourier分析即一种频域分析，Fourier转换理论在成立以来，就一直在信号分析邻域内有着重要的研究地位。

但是，经典的Fourier转换有它的固有缺点，就是在时域里没有任何分辨，转换g(w)在任意有限频段中的信息都不足以确定随机范围里的函数f(x)，这就给工程上带来的很多麻烦。

为了修复这一缺点，加入了窗口或短时Fourier转换

(2)

式中，d为迭代转换次数，函数h(x)即固定的，其叫做窗函数[5]。窗口Fourier转换为一种时频分析。其也存在固有缺点，它的缺点就是窗口的形态是固定不变的。为了修复这一缺点，据此提出了一种新的时频分析方法，称为小波分析，假如函数h(x)满足，那么

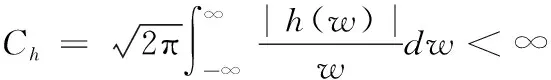
(3)

那么函数f(x)的小波转换为

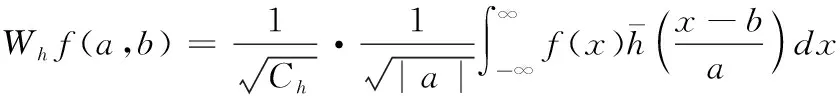
(4)

对应的逆转公式为

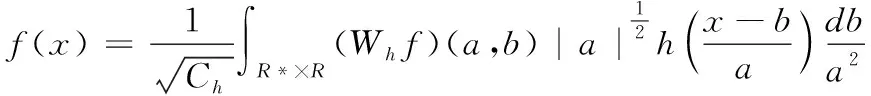
(5)

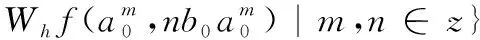
(6)

式中，n表示离散点变换次数。同理，期望讨论系

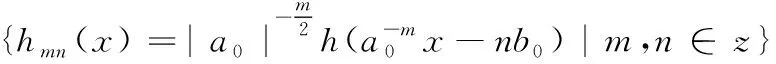
(7)

这样就可以建造一种框架条件。并且在时域和频域里含有较好的局部化性质的函数h，使得系数：{hm，n|m，n∈Z}建造空间L2(R)的规范正交基。就是正交小波函数。

尽管窗口Fourier转换和小波转换都含有时频分析的性质[6]，但是它们在性质中还是具有差异的，其中最关键的是：窗口Fourier抓换对不同的频率成分，在同一时域里的取样步长都是q0，而小波转换对不同的频率成分在时域上的取样补偿为调节高频者小，低频者大，因此，其能够把信号分解为交织在一起的多种尺度成分，同时对于尺度大小的不同使用对应粗细的空域和时域取样步长，进而可以不断的聚焦到对应的任意微小细节[7]。

2.2 离散小波转换

针对高耸结构损伤识别的实际问题大多都是使用离散小波转换，尤其是在数字信号领域方面，把连续小波变换离散化，当做一种便捷的组成形式，对转换进行二进制离散化[8]。所以，通常把离散化的小波变换成一种二进制小波转换。其取值为a0>1，b0>1。据此拟定

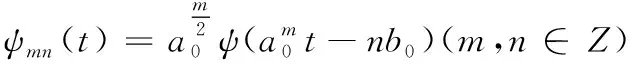
(8)

其中，Z代表整体数所构建的集合，针对f(t)∈L2(-∞，+∞)，将对应的离散小波转换成

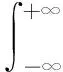
(9)

2.3 时间序列模型

通过上述分析构建时间序列模型，进行时间序列分析，其关键是通过参数模型对所观察的有序随机数据进行分析和处理。作为一种数据处理方法，参数模型在时间序列分析里扮演者关键性的角色。其中，最经典的参数模型是自回归滑动平均模型。针对一种零均值与平稳的时间序列模型xt，t=1，2，…，N，能够拟定一种随机差分方程

xt+a1xt-1+a2xt-2+…+anxt-n

=b1ut+b2ut-1+…+bnut-n+et+d1et-1+…+dnet-n

(10)

式中，xt代表系统t时刻的输出，ut代表系统t时刻的输入，et代表时间误差，ai，bi，di代表系统模型参数，形影的阶层是：ni，nb，nd。

将其后移三次，则式(11)转换成

A(q)xt=B(q)ut+D(q)et

(11)

式(11)能够描述为一种含有额外输入的自回归滑动平均模型，式中，et代表系统的额外输入[9]。采集nb=nd=0，该模型会转换为AR模型。综上所述，本文研究的ARX模型，通过公式能够描述为

A(q)xt=B(q)ut+et

(12)

2.4 伪传递函数

针对N种自由度的粘性阻尼系统，震动微分矩阵方程能够描述成

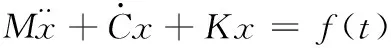
(13)

对该矩阵进行展开，获得

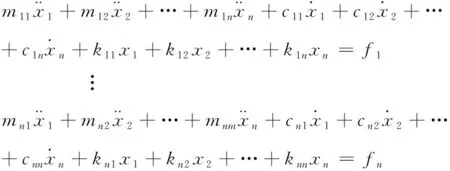
(14)

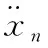
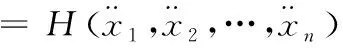
(15)

式中，H代表伪传递函数。

通过式(15)能够得知，伪传递函数里含有高耸结构的自身物理参数[10]。在结构物理参数出现变化时，伪传递函数也会随之出现转变，所以能够把伪传递函数当做指标，对高耸结构的状态进行评测，其中，本文拟定的高耸结构状态主要是结构损伤。

2.5 传递函数构建

凭借伪传递函数的理念，使用ARX模型对其进行建模。利用其自由度的关联性对自由度进行划分，同时挑选其中一种关联性自由度较高的当做参考通道，就是ARX模型的输出，把和其有关联的自由度的响应当做输入，通过ARX模型构建伪传递函数。因为在现实使用里不可能测量全部自由度，所以只对其的自由度进行划分，同时构建伪传递函数。比如：针对第一组，选取第一监测截面的响应当做参考通道，同时将其作为ARX模型的输出，把和其有关联的第二、第三监测截面的响应当做ARX模型的输入，构建第一组的伪传递函数。针对第二组，把第二监测截面的响应当做参考通道，同时将其当做ARX模型的输出，把和其有关联的第一、第二与第三监测截面的响应当做ARX模型的输出，构建第二组的伪传递函数，针对第三组，把第三监测截面的响应当做参考通道，同时将其也当做ARX模型的输出，把和其有关联的第二、第三与第四监测截面的响应当做ARX模型的输入[11]，构建第三组伪传递函数。以此类推，能够构建通过不同监测截面的响应当做参考通道的伪传递函数。在高耸结构的某个截面出现损伤时，和其有关联的自由度之间的伪传递函数也会随之转变，经过伪传递函数的转变对高耸结构的损伤进行定位，大体的过程如图1所示。

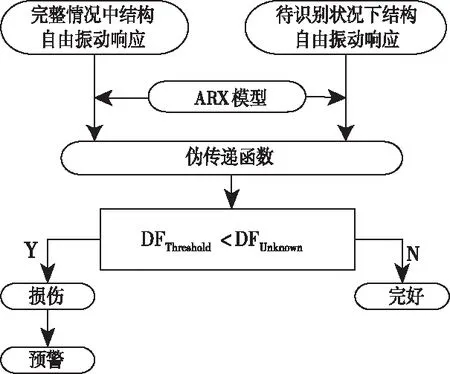
图1 流程图

2.6 损伤阈值下识别

通过高耸结构在正常状态下的响应构建每个分组的基准伪传递函数，对每个状态分组的响应进行融合，设定每个分组的伪传递函数的融合度是

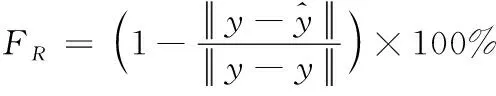
(16)

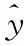
利用上述定义将正常的高耸结构状态与待识别的高耸结构状态[12]，利用融合度的差值进行损伤识别

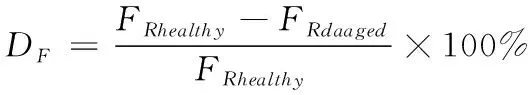
(17)

式中，FRhealthy代表正常状态的高耸结构融合度，FRdaaged代表待识别的高耸结构融合度。

3 仿真证明

仿真环境为Intel Celeron Tulatin1GHz CPU、384MB SD内存的硬件环境以及MATLAB6.1的软件环境。

本文实验使用一种简支的高耸结构钢梁作为实验对象。结构的相关参数是：10号工字钢，跨度为4000mm，弹性模量E=320GN/m2，横向截面面积A=14.44cm2，截面惯性矩Ix=356cm4。

实验简支量的模型见图2。

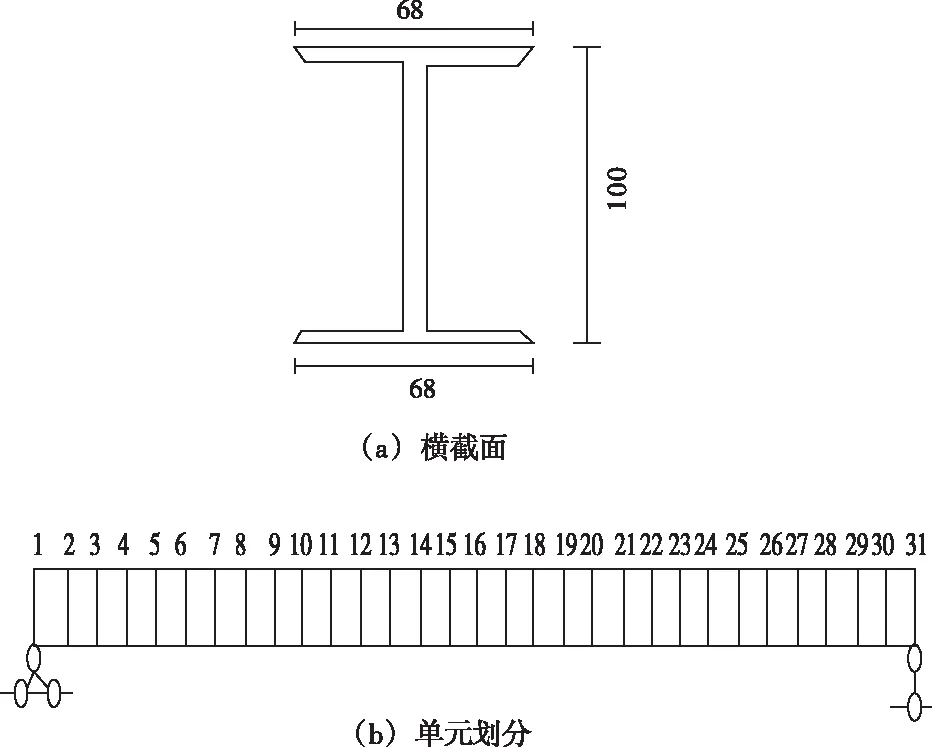
图2 实验简支梁模型

从振动稳定开始收集信号，在2.2s时取出弹簧，就是模拟损伤发生在2.2s时收集到4.187s里简支梁振动加速度信号，同时进行积分计算获得位移和跨速度的时程图，如图3所示。

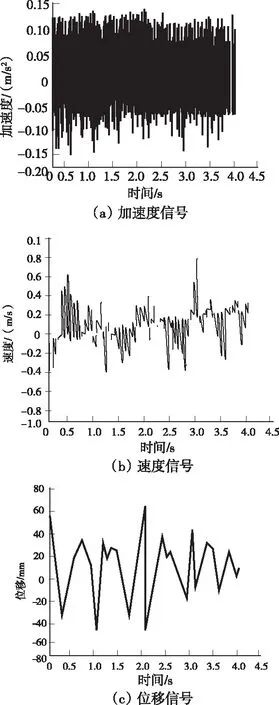
图3 位移、速度、加速度信号

通过图3能够得知，在高耸结构出现损伤时，其速度、加速度与位移信号都会出现变化，本文方法能够清晰的识别到这些信号的转变，然后通过比对阈值来精准的识别高耸结构的损伤区域。

为了更进一步的证明本文方法的实用性，将文献[2]方法和文献[3]方法与本文方法进行高耸结构损伤识别对比，对比的结果如图4所示。

图4 不同方法的高耸结构损伤识别结果

通过图4能够看出，使用本文方法对高耸结构的损伤区域进行识别，能够清晰的获取出损伤区域的位置，同时识别结果较为精准，而文献[2]方法和文献[3]方法虽然也能够识别出大体的损伤区域，但其识别的损伤区域出现了漏检的问题，这是因为，文献[2]方法和文献[3]方法只通过了基础信号来识别损伤区域，其虽然能够识别出高耸结构是否出现损伤，但无法对高耸结构损伤的位置进行精准的识别。

4 结论

针对高耸结构损伤识别时出现的识别效率慢和识别精准度低的问题，本文提出了一种振动信号Fourier分析下高耸结构结构损伤识别方法。并通过实验得出如下结论：

1)将损伤信号转换成连续的离散化小波后，构建时间序列模型，分析有序随机数据进行，从而获得高耸结构损伤的加速度、位移与速度信号，在这个过程中，对损伤区域的损伤识别效率得到优化。

2)挑选自由度粘性阻尼系统其中一种自由度的相应值当做参考通道，使用构建高耸结构在正常状态下的响应构建高耸结构的损伤阈值，将上述得到的信号与损伤阈值进行对比，损伤区域定位效果较强，识别精准度较高。