基于时频特征的旋翼目标微动参数估计方法

宋村夫，曲智国，胡旭超

(1.武警上海总队通信大队，上海 200050；2.空军预警学院，湖北 武汉 430014)

1 引言

在现代信息化战争中，旋翼目标由于体积小、受地形限制小、机动性强等优势在军事竞争中扮演着越来越重要的角色[1]。同时在民用领域，风力发电也正在蓬勃发展，风力涡轮机本质也为一种旋翼微动目标[2]。旋翼目标所产生的微动特征包含着目标的结构、运动特点等相关信息，通过其提取微动参数，对旋翼目标的探测、分类和识别具有重要的意义，因此在军用和民用领域具有广阔的研究场景[3][4]。2006年V.C.Chen提出将目标及其它组件除整体质心运动之外的旋转、振动、以及翻滚等细微的运动形式称为微动，同时提出目标微动会对雷达回波信号产生频率调制，这种由微动引起的多普勒效应被称为微多普勒效应[5]。

目前相关领域专家学者都提出了一些有关微动特征参数提取的技术，其主要包变换域的微动参数提取、基于图像域的微动参提取、基于压缩感知的微动参数提取等[6]。文献[7]提出了一种基于变换域的短时迭代自适应-逆Radon变换(STIAA-IRT)的微多普勒特征提取方法，但是该方法步骤繁琐，计算量大；文献[8]提出了一种基于相位信息的微动参数提取方法，但是需要先解决相位缠绕问题；文献[9]提出利用自相关函数峰值与回波间的对应关系实现了对微动的旋转频率的提取，但是该方法只用于单一周期的回波，在实际应用中局限性大，适应性不高。

针对以上问题，为了进一步有效地提取旋翼目标的微动参数，本文提出了一种基于时频特征的旋翼目标微动参数的提取方法，对叶片旋转频率、叶片初始相位和叶片长度实现了快速提取。首先，构建了旋翼目标雷达回波模型，在此基础上利用分析了旋翼目标回波的时频特征，并利用该时频特征分析了“时频闪烁”与微动参数间的对应关系，最后在时频域利用图像特征实现了微动参数的提取。通过仿真表明，该方法不仅可以实现对旋翼目标叶片的微动参数的快速、高精度的提取，同时该方法还可适用于多个旋翼目标场景下的微动参数提取，且具有一定的抗噪性能。

2 旋翼目标雷达回波建模与分析

以旋翼目标为三叶片构造为例，为简化分析，假设旋翼目标和雷达处在同一平面。以旋翼目标的叶片旋转中心为原点，建立如图所示坐标系。其中，B为雷达站，r为雷达视线(LOS)，θ叶片旋转角，R为雷达中心距离旋翼目标旋转中心距离，li为叶片上散射点距离旋转中心的长度，li≪R。

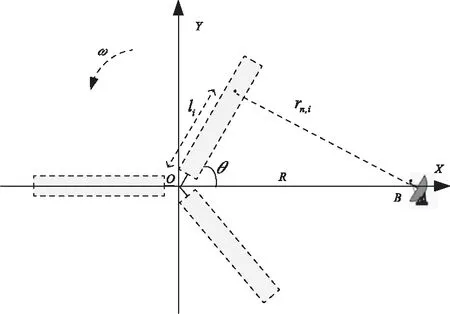
图1 旋翼目标回波模型

假设雷达发射信号p(t)=exp(-j2πfct)[10]，fc为载频，则旋翼目标单个散射点的基带回波信号可表示为

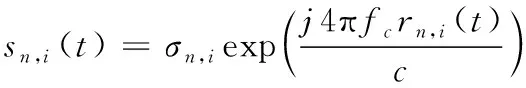
(1)

其中，σn，i为第n个叶片上第i个散射点的散射系数，rn，i(t)为第n个叶片上第i个散射点到雷达的距离。

由于li≪R，则叶片散射点与雷达间的距离rn，i可由菲涅尔近似写为[11]

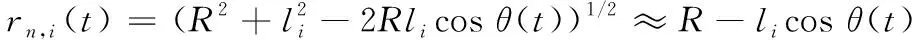
(2)

其中

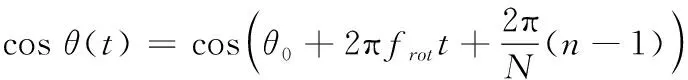
(3)

式中，θ0为该叶片初始旋转角，frot为叶片旋转频率，单位为r/s。

假设旋翼目标上有N个叶片，每个叶片上有K个散射点，则其回波信号可表示为

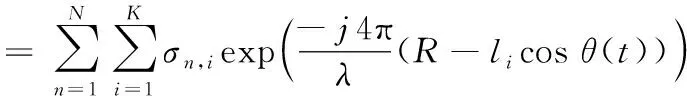
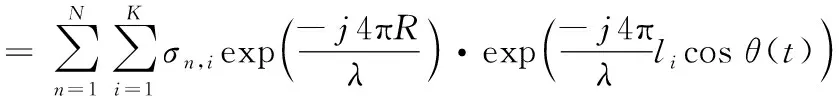
(4)

其中，exp(-j4πlicosθ(t)/λ)为多普勒项，包含了旋翼目标的多普勒信息。

在均匀散射前提下，每个散射点的散射系数可看作是相等的，散射点间隔d=L/K-1，则li=d(i-1)，式(4)可作如下变换：

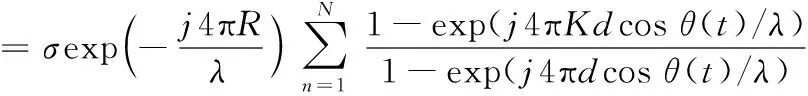
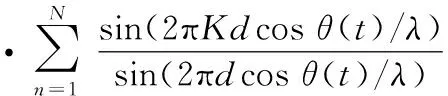
(5)

当散射点间隔d趋近于0时，由近似可得sin(2πdcosθ(t)/λ)≈sin(2πdcosθ(t)/λ)，则式(5)可近似为

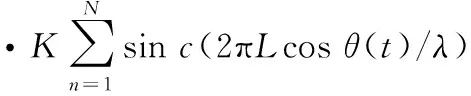
(6)

由式(6)可以看出，旋翼目标的回波幅度受辛克(sinc)函数调制，当cos(θ)=0时，旋翼目标回波才达到sinc函数的峰值，而此时旋翼目标叶片与雷达视线LOS的夹角θ为±π/2，所以只有当叶片与雷达视线LOS垂直时，叶片回波才达到最大值，这被称作时域“闪烁”现象[12]，该时刻被称作“闪烁”时刻。单个叶片在一个旋转周期内可与LOS垂直两次，因此会产生两次“闪烁”现象。

同时，旋翼目标散射点的多普勒频率可以表示为

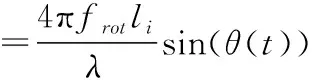
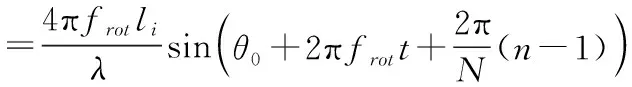
(7)

由于各散射点的旋转半径不同，因此各散射点具有不同的线速度vi=ωili，所以散射点的多普勒频率也是不同的。由式(7)可知旋翼目标单个叶片的回波频率由各散射点的多普勒频率组成

fd1(t)=[fd11(t)，fd12(t)，…，fd1N(t)]

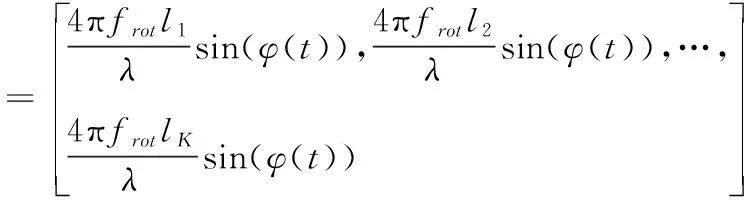
(8)

此外，旋翼目标各散射点的回波多普勒频率是一个随时间变化的量，随着旋转角度的变化，单个散射点的多普勒频率呈现出正弦变化趋势，其周期与叶片旋转周期保持一致。而对于某个t时刻而言，旋翼目标叶尖的散射点具有最大的多普勒频率

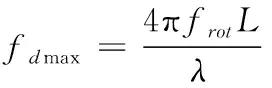
(9)

而叶片旋转中心附近的散射点多普勒频率近乎为零。因此旋翼目标叶片回波的多普勒频率实际上是一个较宽的频率带，其范围为[-4πfrotL/λ，4πfrotL/λ]，当叶片转向雷达方向时，其频率为正，当叶片背离雷达方向时，其多普勒频率为负，其叶片转向与频率正负关系如图2所示。

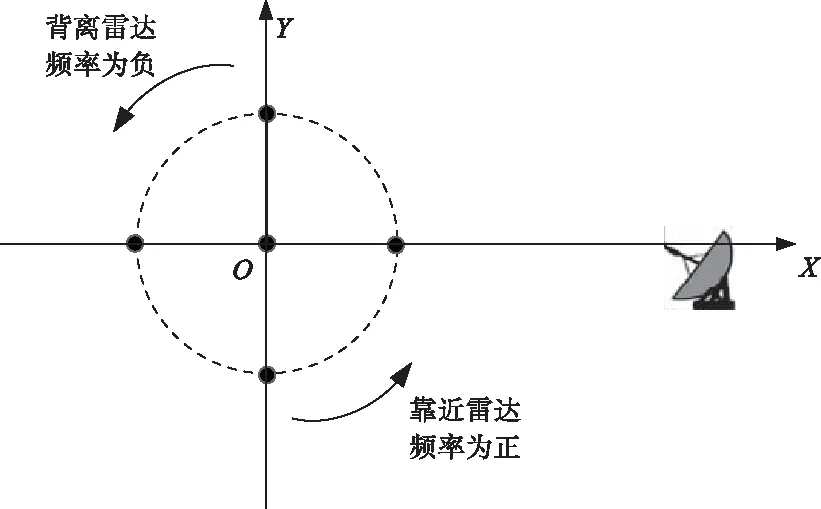
图2 多普勒频率正负示意图

3 基于时频特征的微动参数提取原理

3.1 旋翼目标时频特征分析

由式(8)可知，旋翼目标的多普勒频率是随时间变化的量，因此其回波实际是一种时变非平稳信号。而常规雷达信号处理是建立在平稳信号的基础上的，其频域分析通常常采用傅里叶变换，只能从整体上表示信号的频率构成，无法反映出信号的频谱特性随时间变化的情况。所以频域分析方法不再适用于旋翼叶片回波这一非平稳时变信号，需要利用时频域联合分析处理的方法来对回波信号进行分析[13]，本文采用Garber-短时间傅里叶变换(Garber-STFT)作为旋翼回波时频联合分析方法。

短时傅里叶变换是通过对信号加滑动的时间窗，在时间窗内的信号可看作是平稳信号，因此将长的非平稳信号等价于一系列短平稳信号的叠加，通过时间窗内的信号进行频域变换表示该时刻内信号的频谱特征，由此得到了非平稳信号的时频联合分布，其表达式为：

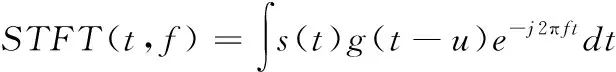
(10)

式中g(t)为窗函数，其中u为窗函数的长度.当g(t)为高斯窗函数时，该短时傅里叶变换就是Garber变换，STFT时频分析过程可以如图3所示。

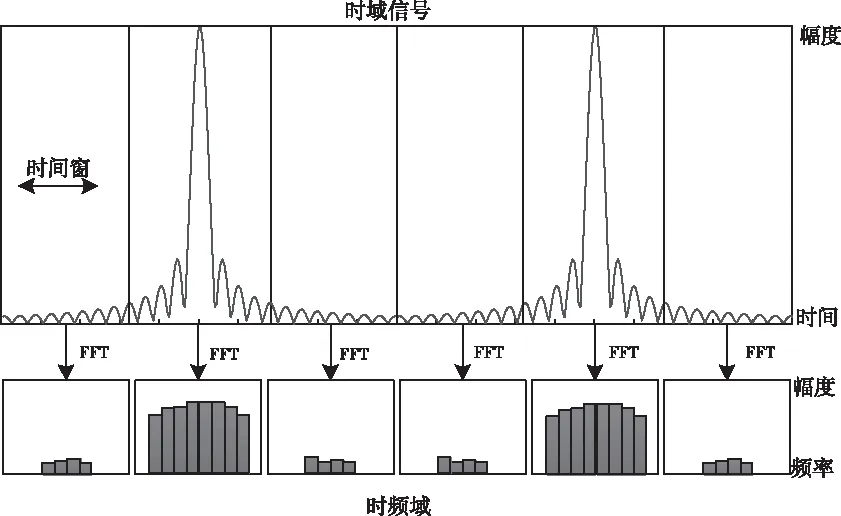
图3 STFT变换示意图

当高斯时间窗滑动到以时域闪烁为中心的信号时，回波信号显示为一个相对完整的辛格峰值包络形式，根据傅里叶变换关系，此时该段信号的频域为矩形包络rect(f)形式，即旋翼目标回波在“闪烁”时刻频率为矩形频带，这被称作旋翼叶片回波在时频域的“闪烁效应”，与时域“闪烁”具有一致性。而当高斯时间窗滑动在非闪烁时刻时，此时回波主要是由叶尖和旋转中心的散射点反射的强电磁散射回波组成，所以在这些时刻的微多普勒特征主要表现为由叶尖引起的正弦曲线包络形式和旋转中心散射点引起的零频带组成。

综上，旋翼目标回波时频特征具有以下特点：

1) 旋翼目标回波时频特征主要由三部分组成：由旋转中心引起的零频带、叶尖引起的正弦包络和以及回波峰值产生的时频“闪烁”。

2) 时频“闪烁”与旋翼目标旋转周期具有对应关系。在一个叶片旋转周期内时频域“闪烁”两次，且只在叶片与LOS垂直时发生。其中，当叶片由背离方向转向雷达方向时，为“正闪烁”，其频率区间为[0，fmax]，由靠近转向背离雷达时，为“负闪烁”，其频率区间为[-fmax，0]。

3) 由于旋翼目标回波峰值积累了大量回波能量，相应地，其时频“闪烁”也具有很高的能量。

3.2 旋翼目标叶片旋转频率提取

由于旋翼目标回波的“时频”闪烁现象与其旋转周期具有对应关系，因此可以通过计算相邻闪烁频带间的时间间隔来估计旋翼目标的旋转频率。以三叶片的旋翼目标为例，由于相邻两个叶片间隔120o，所以对于时频“闪烁”而言，相邻两个同向“闪烁”间的时间间隔为1/3个旋转周期，假设同向闪烁时刻间的间隔Δt，那么旋翼目标叶片的转速估计值为

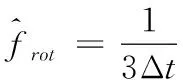
(11)

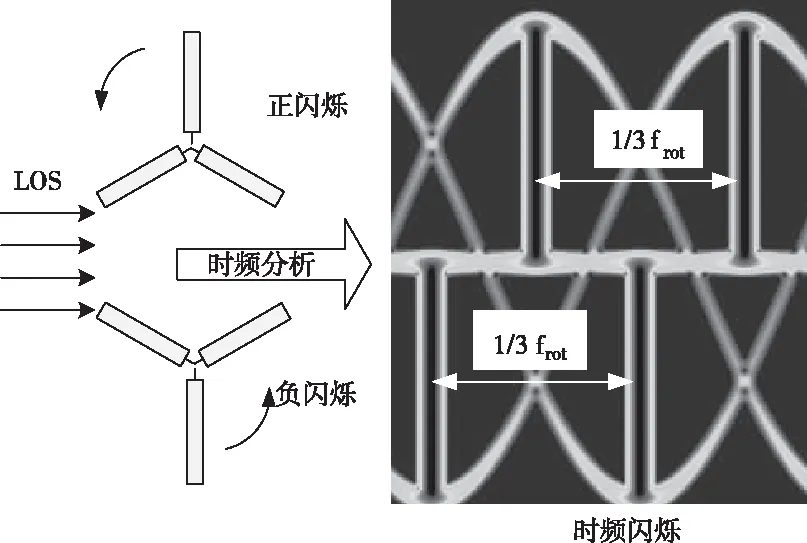
图4 叶片转动与闪烁时刻对应关系示意图

对同向闪烁时刻间的间隔Δt的求解，可以利用图像处理技术手段[15]对时频图进行预处理以提取Δt。由于回波中除旋翼目标外往往还包含大量的噪声，因此首先需要对时频图像进行降噪处理。其次，对降噪后的时频图进行二值化处理，提取时频“闪烁”特征，由于时频“闪烁”回波能量较强，因此通过设置能量门限η实现对时频图的二值化处理，剔除与时频“闪烁”无关的图像信息。同时由于二值化结果较为粗糙，还需要进一步作平滑处理。

旋翼目标回波时频“闪烁”频率带受STFT分辨率的影响具有展宽效应，其闪烁频带往往具有一定的“宽度”，因此在横向占据多个时频单元，该展宽效应可能会造成Δt估计误差的产生，所以对每个频带宽度都选取该横向宽度的中间时频单元为计算单元，这样有利于消除展宽效应，提高叶片旋转频率的估计精度。

3.3 叶片初始相位提取

基于时频特征的旋翼目标微动参数提取方法不仅可以提取叶片的旋转频率，同时还可以根据闪烁频带出现的位置估计叶片的初始相位。假设初始时刻t0的叶片初始相位为θ0，其到第一“闪烁时刻”为t1，此时叶片转过了θ1，其中θ1=2πfrott1，其角度关系如图5所示。因此以“闪烁”作为参照点，利用几何知识可得叶片的初始相位估计值为

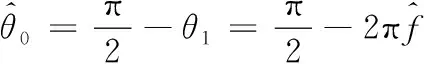
(12)

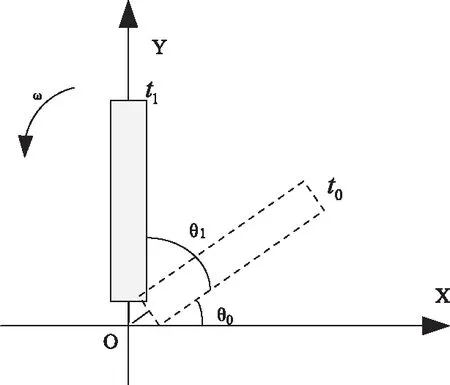
图5 叶片旋转角度关系示意图

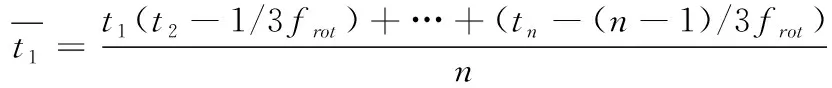
(13)

由式(8)可知，旋翼目标同一叶片上的散射点具有相同的初始相位，不同叶片上的散射点初始相位不同，相邻连个叶片间的初始相位相差2π/3，其它叶片的初始相位可在一个叶片的初始相位估计值0基础上加上相应的叶片角度间隔即可。

3.4 旋翼叶片长度提取

由式(9)回波频率的最大值可知，其回波最大频率与旋翼的转速和叶片长度有关，因此旋翼叶片的长度可由式提取

(14)

fdmax可由时频图中频率范围直接获取，利用式(11)可以得到旋翼转速的估计值，

同时，基于时频特征的旋翼，目标微动参数提取方法也可适用于多个旋翼目标的场景，如对风电场中多个旋翼目标微动参数的提取。由于各旋翼目标间旋转频率均不相同，因此其所有散射点中的最大的多普勒频率也不尽相同，也就是说其时频“闪烁”的频带范围不同，所以可以通过频带范围区分不同的旋翼目标，再根据每个旋翼目标的同向闪烁时刻间的间隔即可计算其叶片旋转频率。

4 仿真与分析

为了验证本文方法对旋翼目标回波的微动参数提取方法的有效性，以三叶片风轮机为旋翼目标进行仿真，雷达仿真参数为：脉冲重复频率为1000Hz；载波频率fc=1GHz；观测时间为2s；雷达波束与风轮机叶片旋转中心距离为20km；风轮机叶片长度均为L=20m。同时雷达波束在风轮机叶片上发生均匀散射，且叶片上散射点间隔均为d=λ/10，所加噪声为高斯白噪声。

仿真1：单风轮机回波微动参数提取

假设某风轮机叶片旋转频率frot=0.4976Hz，叶片初始相位为θ0=1.2129rad，回波信噪比SNR为30dB。其回波微动特征如图6所示。

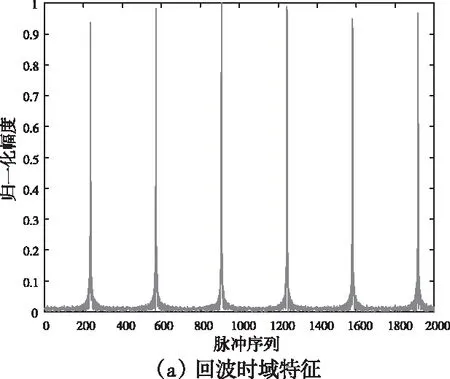
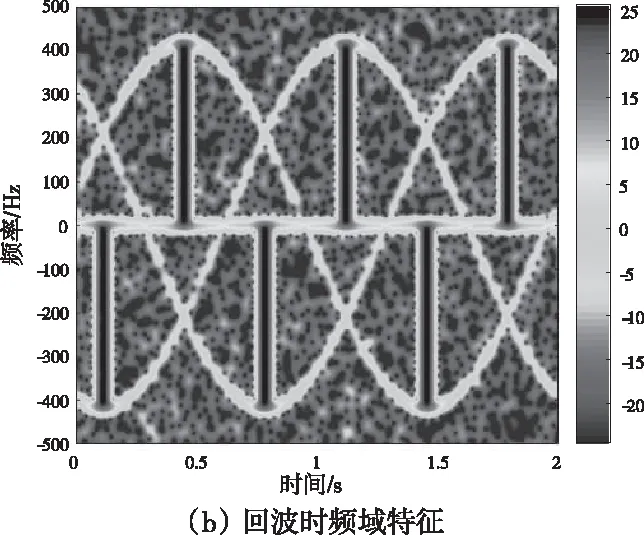
图6 单风轮机回波

由图6可以看出旋翼目标回波呈现辛格函数调制，回波幅度周期性变化，同时其时频域特征由零频带、时频闪烁和正弦包络三部分组成。因此通过回波时域特征和时频域特征可以直观看出风轮机回波的周期性，但是难以直接精准的提取其叶片旋转频率和叶片初始相位。在时频域对回波进行降噪、平滑处理和二值化处理，其时频闪烁提取结果如图7所示，其中二值化能量门限η=20dB。

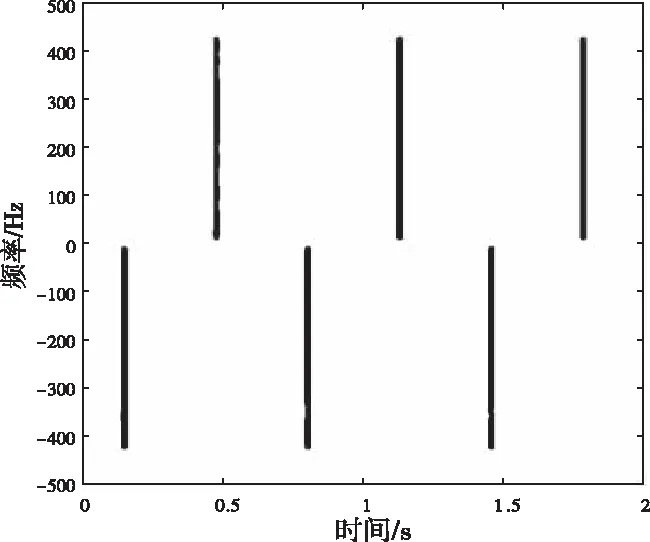
图7 时频“闪烁”提取结果

利用图7中闪烁提取结果，通过寻峰函数可以得到时频“闪烁”负向频带的闪烁时刻分别为t1=0.1140s，t2=0.7835s，t3=1.4535s，则叶片旋转频率估计值为rot=0.4978Hz，与仿真设置值的误差为0.04%，同时，由式(12)可以求得叶片初始相位0=1.2143rad，与仿真设置值的误差为0.12%，相应地，由时频图可知，fdmax=416.87Hz，代入式(14)可知其叶片长度估计值为=19.9920m，其误差为0.4%。由以上结果可知，该微动参数估计结果具有较高的精度，误差均在可接受范围内。

仿真2：多风轮机回波微动参数提取

当多个风轮机分别位于不同距离单元时，可分别对不同距离单元逐个进行微动参数提取，其本质与单个风轮机回波微动参数提取无异。本仿真主要考虑的是在同一距离单元内具有多个风轮机回波，风轮机间的参数均不相同。因此假设距离雷达20km附近有一风电场，场内有三台型号相同风轮机，其叶片转速分别为fr1=0.5282Hz，fr2=0.5025Hz，fr3=0.4976Hz，其叶片初相对应分别为θ01=0.1148rad，θ02=1.352rad，θ03=0.7253rad，其它参数与仿真1保持不变，不考虑风轮机叶间的相互影响，其回波时域与时频域微动特征如图8所示。

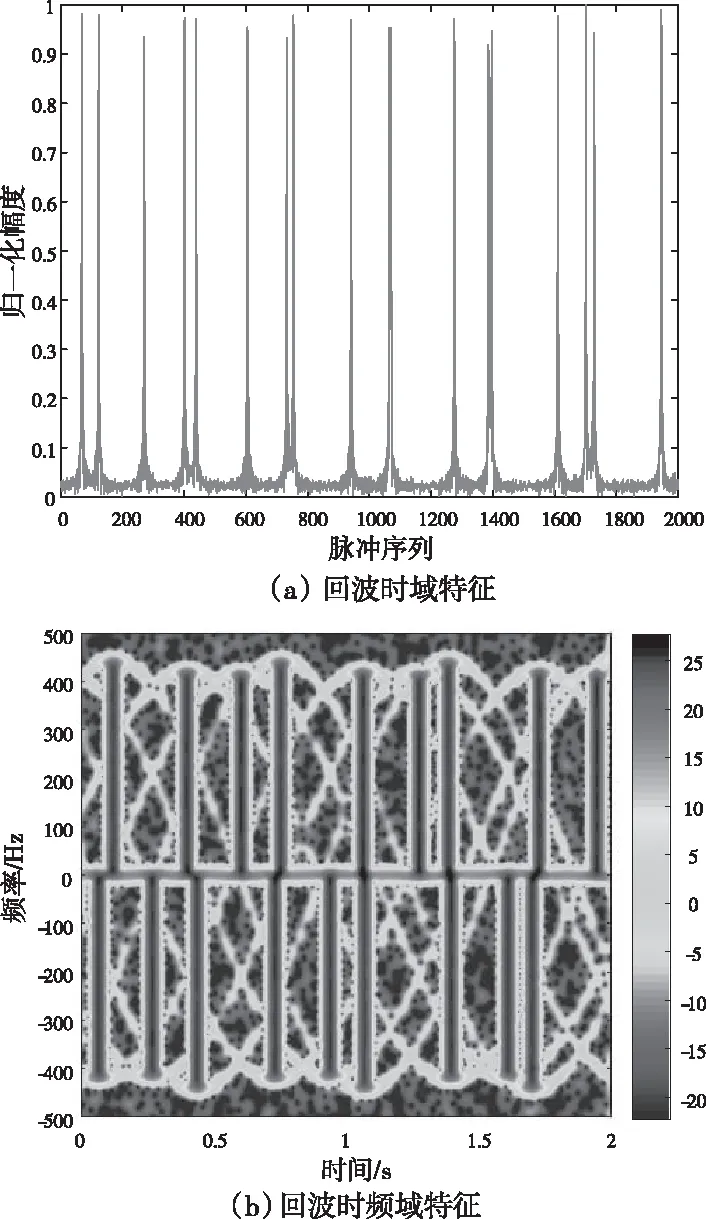
图8 多风轮机回波

通过图8可知，由于三台风轮机叶片旋转频率各不相同，多风轮机回波时域和时频域特征不同于单个风轮机，其回波周期特性难以通过时域直接体现出来，文献[9]所提利用相关函数提取方法失效。但由于不同风轮机叶片旋转频率不同，因此其时频域“闪烁”频带范围也不相同，通过闪烁频带范围(时频图中时频闪烁的长度)即可区分不同风轮机的回波。对多风轮机回波时频图提取时频“闪烁”结果如图9所示。

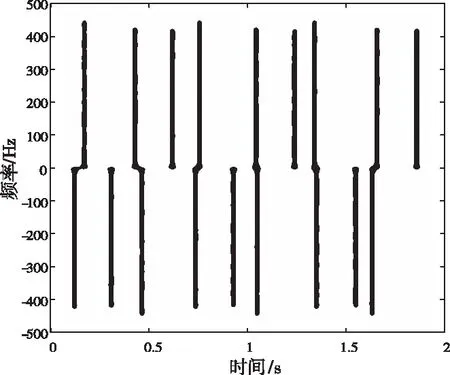
图9 多风轮机回波时频闪烁提取结果

通过时频提取结果结果，可以区分出风轮机1的负闪烁时刻为0.4380s、1.0695s、1.7000s，风轮机2的负闪烁时刻为0.0685s、0.7320s、1.3955s，风轮机3的负闪烁时刻为0.2700s、0.9390s、1.6125s。多风轮机微动参数提取结果如表1所示。

由表1提取结果可以看出，本文所提基于时频特征的微动参数提取方法对多个风轮机的多个旋转频率和初始相位实现有效提取，其中旋转频率误差小于0.5%，初始相位误差小于2%，叶片初相估计误差明显大于旋转频率误差，这是因为叶片初相需要利用旋转频率估计值求解而造成了误差积累，但是该误差在可接受范围内。因此本文所提方法可适用于多个风轮机场景下的微动参数提取。

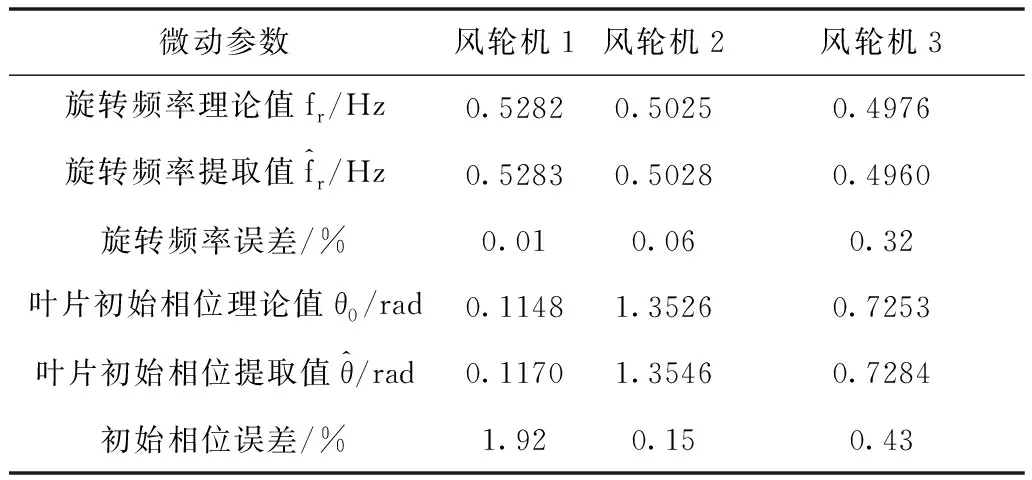
表1 多风轮机微动参数提取结果

仿真3：不同SNR下估计误差分析

为验证在不同信噪比(SNR)下本文方法提取微动特征的鲁棒性，本文进行M次蒙特卡罗实验，并进行均方根误差(Root Mean Square Error，RMSE)分析。

对于估计的旋转频率，其RMSE的表达式为

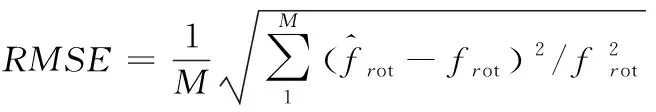
(15)

本文取M=100，设置SNR的范围为2～40dB，步进2dB，图10为不同SNR场景下估计结果的RMSE。

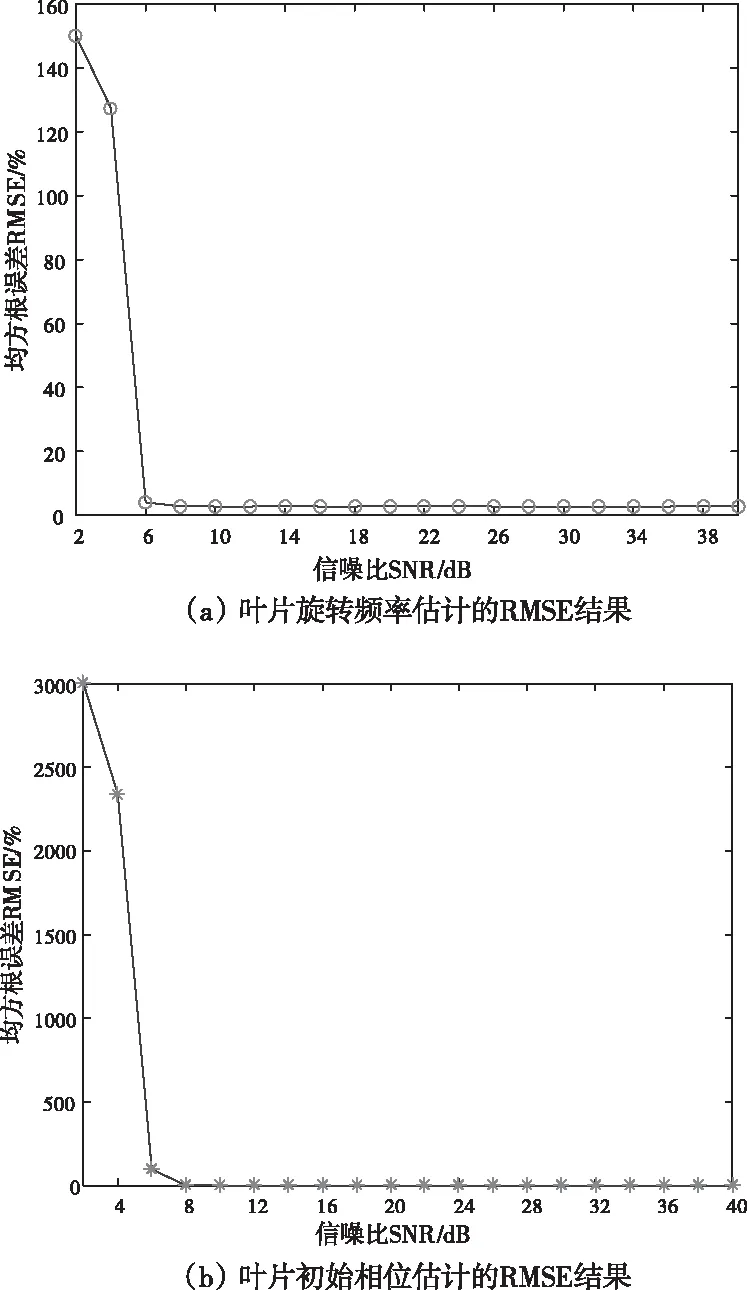
图10 估计误差结果

由图10(a)可知，估计旋转频率的RMSE随着SNR的提高而降低，当SNR小于6dB时，该方法估计的叶片旋转频率误差较大，这是由于噪声功率过大无法通过时频图像提取有效信息。当SNR达到6dB以上时，RMSE的值小于1%，说明该方法在高信杂比条件下具有很高的精度，此时RMSE趋于稳定，说明该算法具有一定的稳健性。

图10(b)为叶片初始相位估计值的RMSE结果，由图可知，初始相位的估计值同样也随着SNR的提高而降低，在6dB以下误差精度较大，得不到初始相位的有效信息，此时叶片初始相位RMSE结果大于旋转频率的RMSE，也是由于噪声功率过高，在时频域无法提取到有效信息，同时，叶片旋转频率误差过大在初始相位估计时也造成了误差积累。当SNR在6dB以上时，初始相位估计误差区域稳定且小于2%，此时算法具有较好的参数估计精度。

5 结论

旋翼目标的微动参数在目标探测、识别领域具有重要意义。本文提出了一种基于时频特征的雷达旋翼目标微动参数估计方法。该方法主要通过分析旋翼目标回波时频特征，利用时频域“闪烁”特征与微动参数间的对应关系，在时频图像域实现了对微动参数的有效估计。仿真结果表明该估计方法不仅可以实现对单个旋翼目标的叶片旋转频率、叶片初始相位和叶片长度的高效、快速提取，而且在多旋翼目标场景下也同样适用。同时该估计方法在高信杂比条件下，估计结果具有良好的精度且算法具有一定的稳定性。