基于L1输出反馈自适应方法的火箭姿态控制

苏秀健，吴国强，周文雅，贺从园

(1.大连理工大学航空航天学院，辽宁 大连 116024；2.上海航天控制技术研究所，上海 201109)

1 引言

伴随着对火箭运载能力等方面的不断追求，火箭系统朝着大型、重型发展，新一代运载火箭弹性振动模态频率偏低，且随着其尺寸的增加，考虑到试验规模、研制周期和研制成本等方面，拟取消全箭模态实验，改用子结构实验与模态综合技术代替，因此需要将基于精确模型的PID控制改进为先进的自适应控制等方法[1]。由Cao和Naira提出的L1自适应控制能够在飞行器模型参数发生不确定变化的情况下依然具有良好的目标信号跟踪性能[2-5]，但针对运载火箭尤其是刚—弹耦合箭体的稳定控制而言，L1自适应方法的研究目前比较匮乏。

目前，国内关于L1自适应控制理论的研究主要集中于状态反馈形式，且控制对象皆为刚体，如：无人飞艇[6]，高超音速飞行器[7]等。考虑到被控系统存在状态变量不可测或者不可控的特点，采用全状态反馈的状态反馈L1自适应控制就不再适用[8]，其中包括本文研究对象运载火箭，因此采用输出反馈L1自适应方法对其进行稳定控制，目前关于该形式的研究在外文文献中有所涉猎[9-11]，但针对运载火箭进行相关参数设计、讨论以及仿真的情况较少。

本文以运载火箭俯仰通道为研究对象，基于L1输出反馈自适应方法设计控制器以实现稳定控制，创新点在于探究利用L1控制器自身结构实现刚—弹耦合箭体稳定时低阶频率分布规律，并且结合校正网络思想提出一种实现低频模态运载火箭稳定控制的L1自适应方法。

2 运载火箭动力学模型

依据文献[12]，刚体火箭俯仰通道姿态角动力学方程为

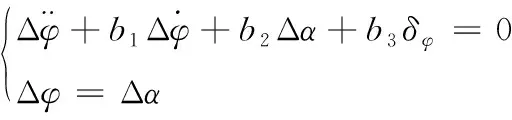
(1)

式中：Δφ为俯仰角，Δα为攻角，舵偏角δφ为控制变量，b1、b2、b3为刚体运动方程系数。

火箭的弹性振动方程可由下面二阶常微分方程描述

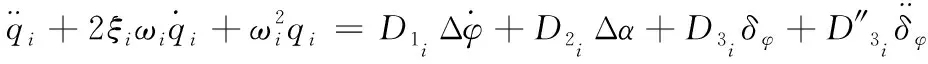
(2)

式中：qi为第i阶弹性振动对应的广义位移，ωi和ξi为第i阶弹性振动广义位移对应的频率和阻尼比系数。

另外姿态测量元件除测量出刚体姿态运动信号外，还测量出弹性振动产生的附加姿态信号

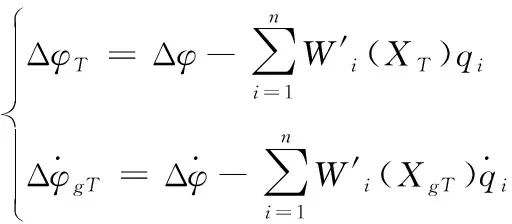
(3)

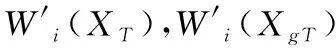
则完整的刚—弹耦合箭体动力学方程如下

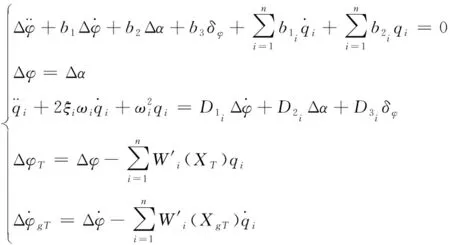
(4)

3 L1输出反馈自适应控制理论

3.1 基本结构

L1输出反馈控制系统由被控对象、状态观测器、自适应律、控制律四部分组成。状态观测器负责估计和监视被控对象的输出及变化，自适应律调节待估计的参数，控制律由初步控制律及低通滤波器组成，初步控制律根据自适应律提供的估计参数和给定的参考信号及时调整控制信号，低通滤波器将控制量中的高频信号滤掉[13]。

1)被控系统

将一个单输入单输出系统描述为以下形式

y(s)=A(s)[u(s)+d(s)]

(5)

式中：u(s)是输入信号，y(s)是系统输出，A(s)是严格正则的传递函数，d(s)是描述模型不确定性及干扰信号d(t)的Laplace变换。

设r(t)为给定的有界连续参考输入信号，控制系统的目标就是设计一个自适应输出反馈控制器u(t)，保证系统输出y(t)跟踪参考输入r(t)经理想传递函数M(s)后的信号，即y(s)≈M(s)r(s)，其中M(s)是最小相位稳定传递函数，则式(5)可重新描述为如下形式

y(s)=M(s)[u(s)+σ(s)]

(6)

式中

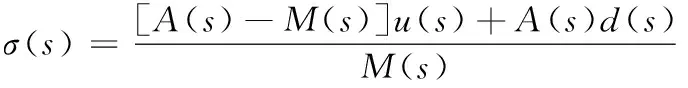
(7)

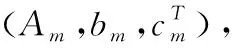
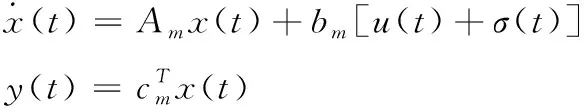
(8)

2)状态观测器

状态观测器与被控对象形式类似，定义如下

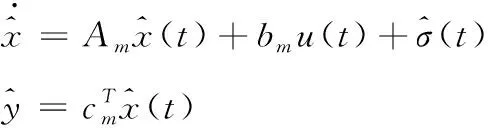
(9)

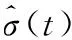
3)自适应律

(10)

式中：Q是正定矩阵，由P是正定对称矩阵可知，总是存在非奇异矩阵使下式成立

(11)

(12)

并且令

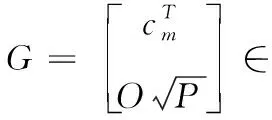
(13)

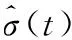
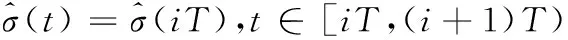
(14)

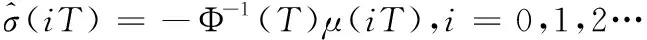
(15)

式中

(16)

(17)

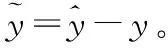
4)控制律

由式(9)可得，状态观测器输出为

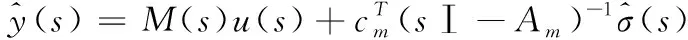
(18)

被控对象与状态观测器具有一致的动力学特性，结合控制器设计目标y(s)≈M(s)r(s)，可得经过低通滤波器C(s)之后的控制律表达式为

(19)

综上所述，L1输出反馈自适应控制的结构如图1所示。

图1 L1输出反馈自适应控制框图

3.2 系统性能分析

引入闭环参考系统式(20)-(22)，它是L1自适应输出反馈控制器的非自适应形式。

yref(s)=M(s)[uref(s)+σref(s)]

(20)

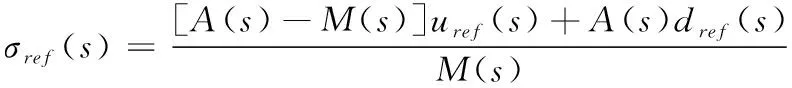
(21)

uref(s)=C(s)[r(s)-σref(s)]

(22)

由(21)和(22)可知

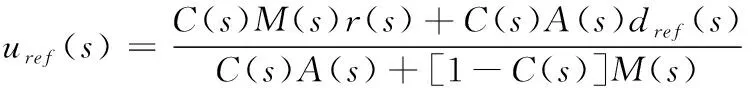
(23)

由式(20)和(21)得：

yref(s)=A(s)[uref(s)+dref(s)]

(24)

将式(23)代入式(24)中得：

yref(s)=H(s){C(s)r(s)+[1-C(s)]dref(s)}

(25)

式中

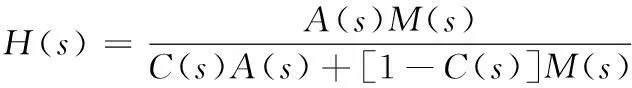
(26)

由式(25)可得，闭环系统稳定(即C(s)和M(s)的选取)应满足H(s)是稳定的，而H(s)的稳定等价于通过下述负反馈环节使被控系统A(s)趋于稳定。

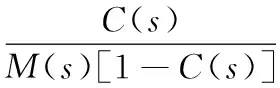
(27)

依据文献[10]可知，通过选择合适的采样时间T，可使下式成立

(28)

(29)

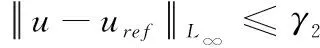
(30)

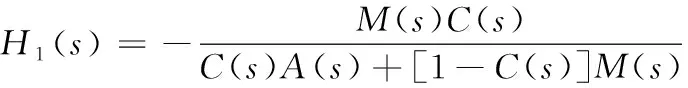
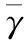
根据上述关系可进一步推得

(31)

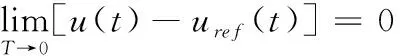
(32)

上式表明可通过减小采样时间T提升跟踪性能，但也对计算机硬件提出了更高的要求[10]。

4 L1自适应控制器设计及仿真

本节首先对刚体火箭设计L1输出反馈控制器参数，其次考虑带有一阶弹性振动信息的刚—弹耦合箭体，考虑到低通滤波器环节一定程度上减小弹性振动的影响，分析实现箭体稳定时火箭低阶频率的分布规律，并提出一种结合校正网络思想设计L1自适应控制器的方法，同时考虑弹性频率发生变化，观察该方法的有效性。被控对象模型参数选取如下[1]

b1=0.0465，b2=-0.0421，b3=0.5674

ω1=8.5，ζ=0.005，D31=16.4286

W′1(XT)=0.0375，W′1(XgT)=0.0375

4.1 刚体火箭控制器参数设计

将理想传递函数M(s)及低通滤波器C(s)选为如下形式

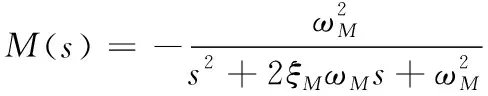
(33)

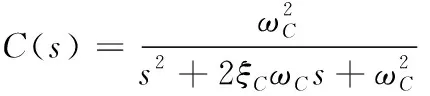
(34)

式中：ξM和ξC分别为M(s)和C(s)的阻尼比，ωM和ωC分别为M(s)和C(s)的带宽。

1)理想传递函数M(s)选取

理想传递函数M(s)可理解为被控系统响应的参考模型，其对系统响应中稳定时间，超调量等暂态性能起决定性作用。M(s)的选取应当参照被控对象特性选取。M(s)参数包括阻尼比ξM和带宽ωM，一般将阻尼比设为良性阻尼比0.7，而M(s)带宽ωM应当与被控对象带宽相近，这样可保证系统响应可实现性。

经分析，被控对象带宽约为0.88rad/s，根据上述内容，选定理想传递函数带宽ωm=1rad/s。

2)采样时间T选取

自适应律中待设计参数为采样时间T，在一定范围内，减小T可提升系统跟踪性能，但T设置过小时，也对计算机性能要求更高，结合工程应用中计算机处理性能一般为5ms-20ms，因此将T设为10ms，即0.01s。

3)低通滤波器C(s)选取

低通滤波器C(s)待设计参数包括阻尼比ξC和带宽ωC，一般将阻尼比选为良性阻尼比0.7。在根据性能要求确定好理想传递函数M(s)之后，依据系统稳定条件(即式(26)稳定条件)确定ωC。为维持系统稳定，C(s)带宽选取有一个下限值，其物理含义是保证实现刚体火箭稳定所需的最小信息量，因此一般C(s)带宽取值越大越好，但到某特定值之后，性能就不再有明显提升，且带宽设置过大时，控制输入中含有高频振荡，考虑到刚—弹耦合箭体的设计，为避免高频弹性振动信息对系统稳定的影响，将低通滤波器带宽设为ωC=6rad/s。

4.2 刚—弹耦合箭体仿真

在火箭姿态控制系统设计中，对于刚—弹耦合箭体的控制，一般需借助于滤波器实现弹性振动信息的过滤，鉴于L1控制结构中具有低通滤波器环节，因此考虑能否利用上节所设计参数实现刚—弹耦合箭体的稳定控制，仿真结果如图2所示。

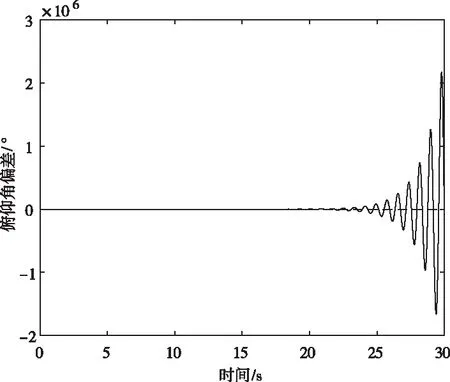
图2 俯仰角输出曲线(刚—弹耦合箭体)

由上图可知，在原参数组成的控制系统作用下，刚—弹耦合箭体最终发散，其原因是低通滤波器带宽与一阶弹性频率点较近，致使控制信号中依然具有较强的弹性振动信息。

为探究利用L1输出反馈自适应控制自身结构实现刚—弹耦合箭体稳定的条件，下面通过假设模型进行分析。控制器参数与上述一致，通过假设弹性对象一阶弹性频率分布情况，观察控制效果，仿真结果如下：

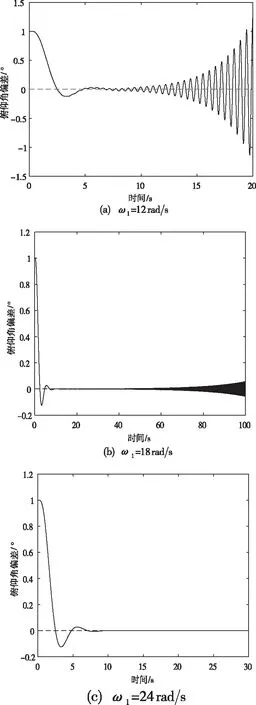
图3 俯仰角输出曲线(假设箭体)

由上图可知，当C(s)带宽与一阶弹性振动频率之间存在2倍关系时，抑制弹性振动的作用开始显现，但仿真后半段被控对象响应发散，说明此时不足以完全抑制弹性振动；当二者存在3倍关系时，效果相对大有改观，总体效果看似能趋于稳定，但将仿真延长后，后半段仍会出现小幅度发散；当二者存在4倍关系时，C(s)带宽与一阶弹性频率之间有充足的余量，可使刚—弹耦合对象完全趋于稳定。因此通过假设模型可知，若通过L1输出反馈自适应控制自身结构实现刚—弹耦合箭体的稳定，需保证C(s)带宽和一阶弹性频率之间满足4倍左右的比例关系，此时低通滤波器能充分抑制弹性振动对系统稳定性的影响。

4.3 结合校正网络的控制器设计与仿真

由上可知，低通滤波器带宽与系统带宽存在相互制约关系，无法通过低通滤波器消除低阶弹性振动影响，故结合校正网络思想设计L1输出反馈控制器实现刚—弹耦合箭体的稳定。

对于弹性振动的稳定来说，有幅值稳定和相位稳定之分。在本例中只考虑一阶弹性振动，因一阶弹性振动模态频率低，相位偏差小，故结合相位稳定思想设计校正网络对刚—弹耦合箭体进行稳定控制[14]。

依据闭环系统稳定条件(即式(26)稳定条件)可知，弹性被控对象A(s)在原反馈控制器C(s)/M(s)[1-C(s)]下的开环频率特性曲线如图4黑线所示。

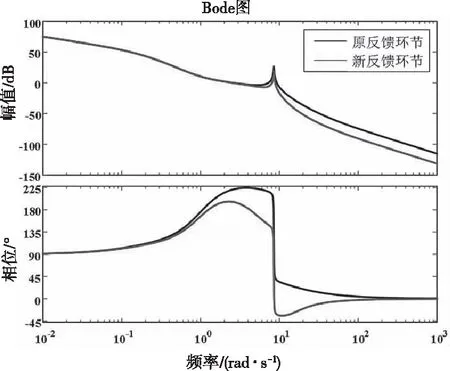
图4 频率特性曲线对比图

由上可知，在原反馈控制器作用下，系统一阶弹性振动频率处幅频曲线L(ω)>0且相频曲线穿越π这条线，故不能保持稳定。因此设计校正网络的思想是：通过设计相位滞后滤波器，使得某频率处之前的幅频曲线及相频曲线与原来保持一致，而在其之后整体向下，以保证在一阶弹性频率处，系统相频曲线不穿越π这条线。

选取如下形式的二阶最小相位滞后滤波器

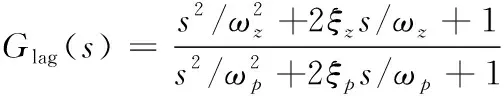
(35)

式中，ξz和ξp分别为阻尼比，ωp为滤波器带宽，其决定频率特性曲线发生变化的分离点，幅值变化量为-40lg(ωz/ωp)。

根据本文研究对象，设定滤波器数值如下：ξz和ξp选为良性阻尼比0.7，ωp设为5.5rad/s，幅值变化量为-16dB，由此可得

将二阶最小相位滞后滤波器Glag(s)与原M(s)做结合，则可得到如下新配置的M(s)

刚—弹耦合箭体在新配置的M(s)和C(s)组成的负反馈环节作用下，频率特性曲线如下结合相位稳定思想可知，通过引入校正网络，实现了一阶弹性振动稳定。

图5 俯仰角输出曲线(ω1变化)

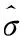
5 结论

针对火箭刚-弹耦合模型开展了L1输出反馈姿态控制器设计，给出了依据火箭特性参数设计规则以及火箭低阶频率的分布对于控制系统的影响情况，同时研究了利用结构滤波器实现弹性抑制的设计方法，取得如下结论：

对于刚—弹耦合箭体而言，当低通滤波器带宽与一阶弹性频率之间满足4倍左右关系时，L1控制器可同时实现刚—弹耦合箭体的稳定；当两者小于上述比例关系时，带宽的选择应优先满足刚性箭体的设计要求，同时必须引入校正网络来消除弹性振动对系统的影响，仿真结果表明，所设计控制器控制效果良好，且弹性频率变化下具有较强的鲁棒性。