坡度对跨座式单轨隧道临界风速的影响

张 雄

(中铁四院集团西南勘察设计有限公司，云南 昆明 650220)

0 引言

跨座式单轨系统由于其造价低、工程量适中、建设占地小、景观效果好、运输客运量适中等优点，在中小城市发展尤为迅速[1-3]。但目前，我国单轨轨道交通系统还处于起步阶段，很多关键技术尚未解决。

根据CJ/T 287—2008《跨座式单轨交通车辆通用技术条件》，跨座式单轨列车所用车轮为橡胶轮胎[4]。路世昌等[5]指出，橡胶轮胎具有高于木材的火灾危险性且烟气生产量巨大。同时，GB 50458—2008《跨座式单轨交通设计规范》[6]“4.3.1车辆主要技术规格”规定其最大坡度为6%。单轨隧道相对密闭且坡度大，发生火灾时，橡胶极易燃烧且火源功率大。在跨座式单轨隧道中发生火灾，由于其大坡度及大火源功率的特点，烟气运动规律必定与无坡度小功率的隧道烟气运动规律不同。如何有效抑制单轨隧道中的烟气，避免烟气回流现象[7]的发生，保障人员安全疏散和消防人员的安全救援，是亟待解决的问题。为了避免烟气回流，工程实践中常采用纵向通风的方法，而临界风速则是纵向通风系统设计中的关键参数，故临界风速一直以来都是隧道火灾的研究热点。

目前，已有大量关于临界风速和坡度之间关系的研究，但是至今对坡度修正系数还存在争议，特别是在大坡度大功率情况下，并没有多少试验数据证实前人研究结果的准确性，还需要大量的试验数据来修正坡度修正系数。因此，本文通过缩尺试验，研究大坡度大火源功率对临界风速的影响。

1 试验台介绍和工况

1.1 试验台介绍

在隧道火灾中，浮力效应起主导作用，火源附近的烟气流动为重力流，因此，模型试验采用Froude准则作为相似准则[14]。本文以柳州市4号线跨座式单轨隧道为原型，建立1∶20的缩尺隧道模型，如图1所示。该模型长度为20 m，截面分为上下部分，上部为直径0.32 m的半圆，下部为宽0.32 m、高0.13 m的长方形，如图2(a)所示。为了便于观察火源及烟气特性，隧道一侧安装有与隧道等长的防火玻璃，宽为100 mm，厚为15 mm，另一侧安装有相同尺寸的防火板，隧道其余部分由2 mm厚的钢板组成，隧道所有钢结构表面涂抹防火涂料以防止钢结构受热变形。防火板、防火玻璃与钢板之间的空隙采用防火泥密封。隧道左侧的顶棚安装1台直径200 mm的轴流风机，如图2(b)所示，风机的转速由变频器控制，可在隧道内提供0～1.2 m/s的均匀风速。该模型隧道置于室内，受自然风影响可忽略。

图1 隧道模型Fig.1 Model of tunnel

图2 隧道示意Fig.2 Schematic diagram of tunnel

火源设置在距离隧道一侧开口9 m处，火源燃料为丙烷，燃烧器大小为0.1 m×0.1 m，气源由加压气罐提供，流量由转子流量计控制。根据SFPE handbook[15]，丙烷燃烧热为46.45 MJ/kg，密度为1.83 kg/m3，根据计算可得，7.90 L/min以及19.75 L/min分别对应热释放速率11.2 kW以及28.0 kW,即对应全尺寸20 MW和50 MW。为测量烟气纵向温度，沿隧道中心线纵向布置56个K型热电偶，距火源0.2 m内间隔为0.1 m，距火源0.2 m至0.4 m内间隔为0.2 m，其余间隔均为0.4 m。温度采集系统使用MT-X型多路温度测试仪，每秒记录1次数据。为测量烟气流动速度，本文试验在隧道水平中心位置、圆顶下方50 mm处设置2个风速测点，如图2(c)所示。风速测量使用精度为0.01 m/s的Kanomax 6036型号的风速测量仪。

1.2 试验工况

周庆等[16]通过数值模拟和试验结果得出在同一个坡度下，纵向通风风速与回流长度近似呈线性关系，因此本文通过线性拟合烟气回流长度和通风风速确定临界风速大小。试验功率为11.2 kW和28.0 kW，根据Froude准则换算，对应全尺寸火源功率分别为20 MW和50 MW，坡度分别为0%，3%和6%。送风方向见图3，逆坡送风时坡度s为负，顺坡送风时坡度s为正。试验工况如表1所示。

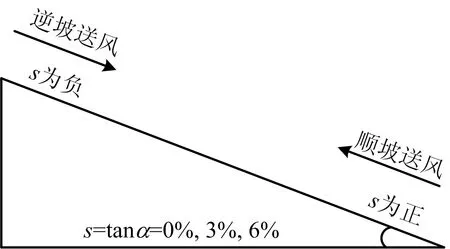
图3 送风方向示意Fig.3 Schematic diagram of air supply direction

表1 试验工况Table 1 Experimental conditions

2 结果与分析

2.1 不同坡度下的临界风速

根据表1所示试验工况进行试验，取烟气回流长度0.5～2.0 m的通风风速进行拟合，确定临界风速：取温升超过10 ℃的位置为烟气回流范围确定烟气回流长度；将烟气回流长度与纵向通风风速作线性拟合，取当回流长度为0时的纵向通风风速作为此工况的临界风速。纵向通风风速和回流长度如表2所示。

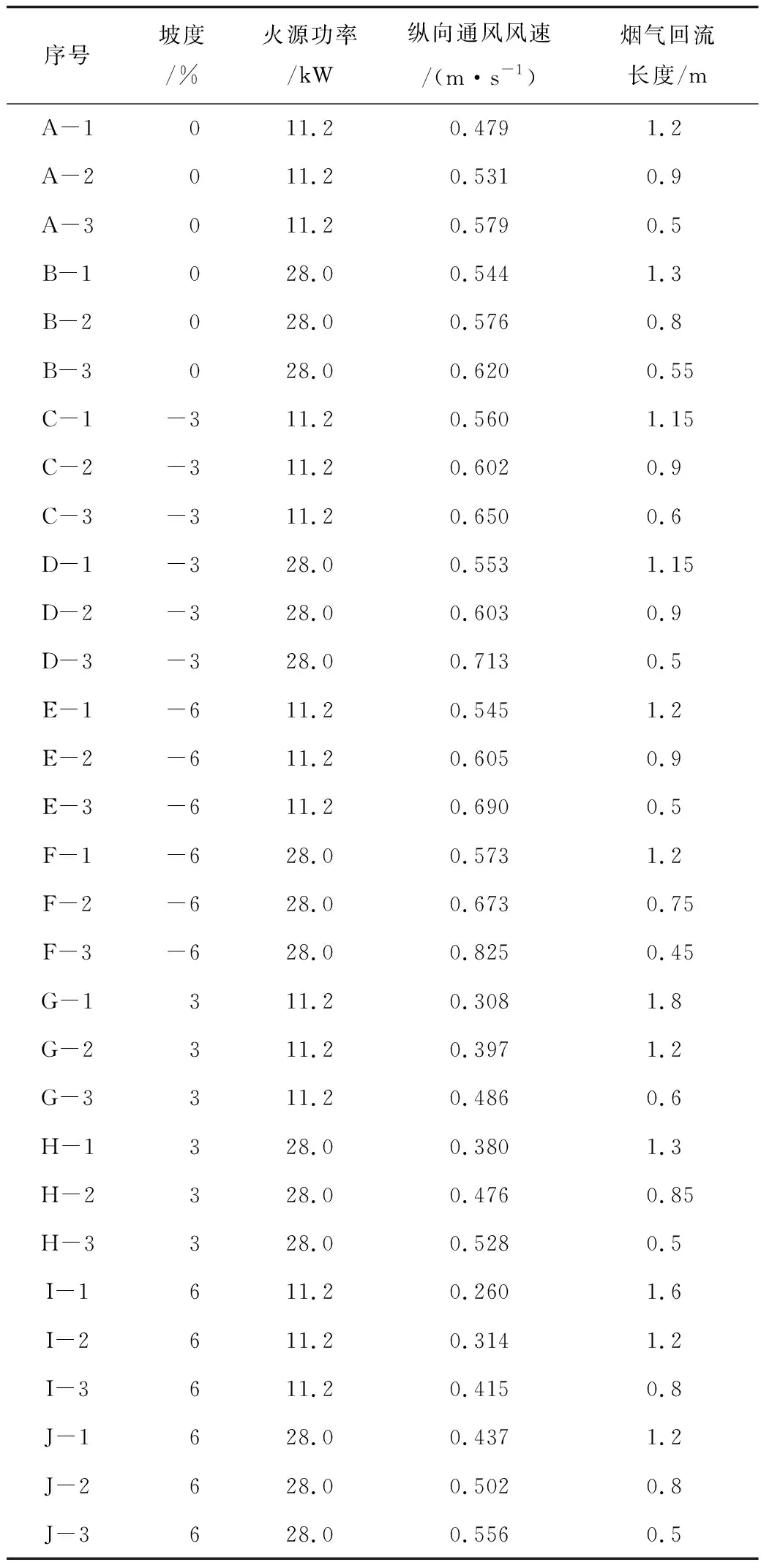
表2 纵向通风风速与烟气回流长度Table 2 Longitudinal ventilation velocity and recirculation length of smoke

采用上文所述方法计算临界风速，见表3和图4。

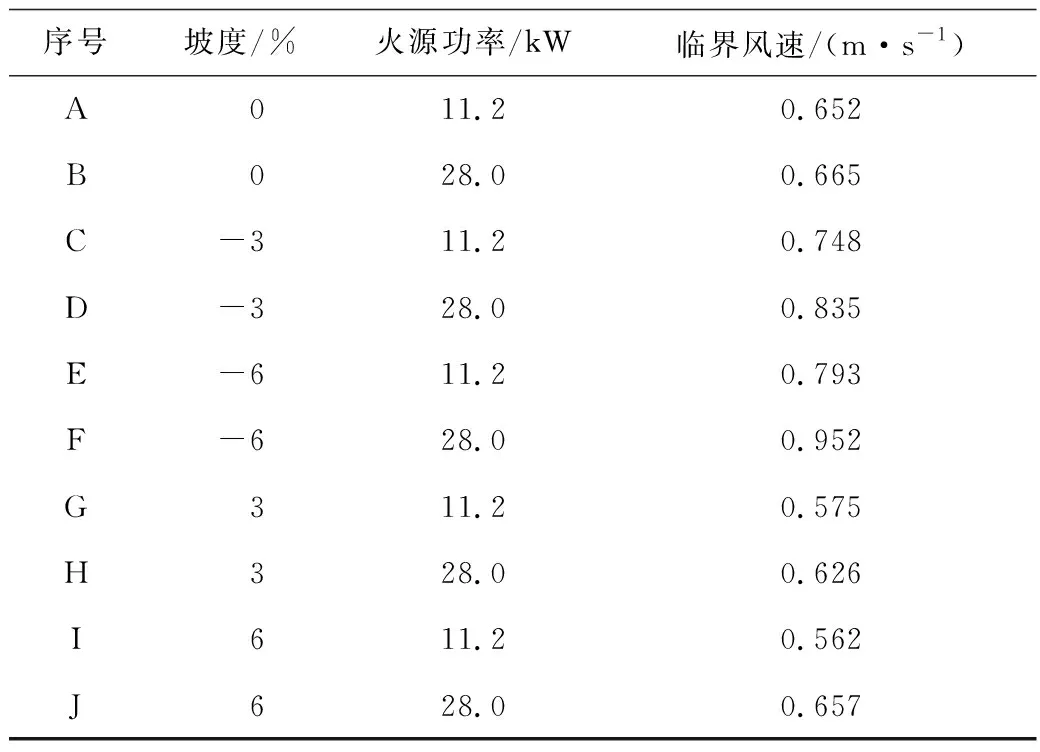
表3 临界风速汇总Table 3 Summary of critical wind velocities

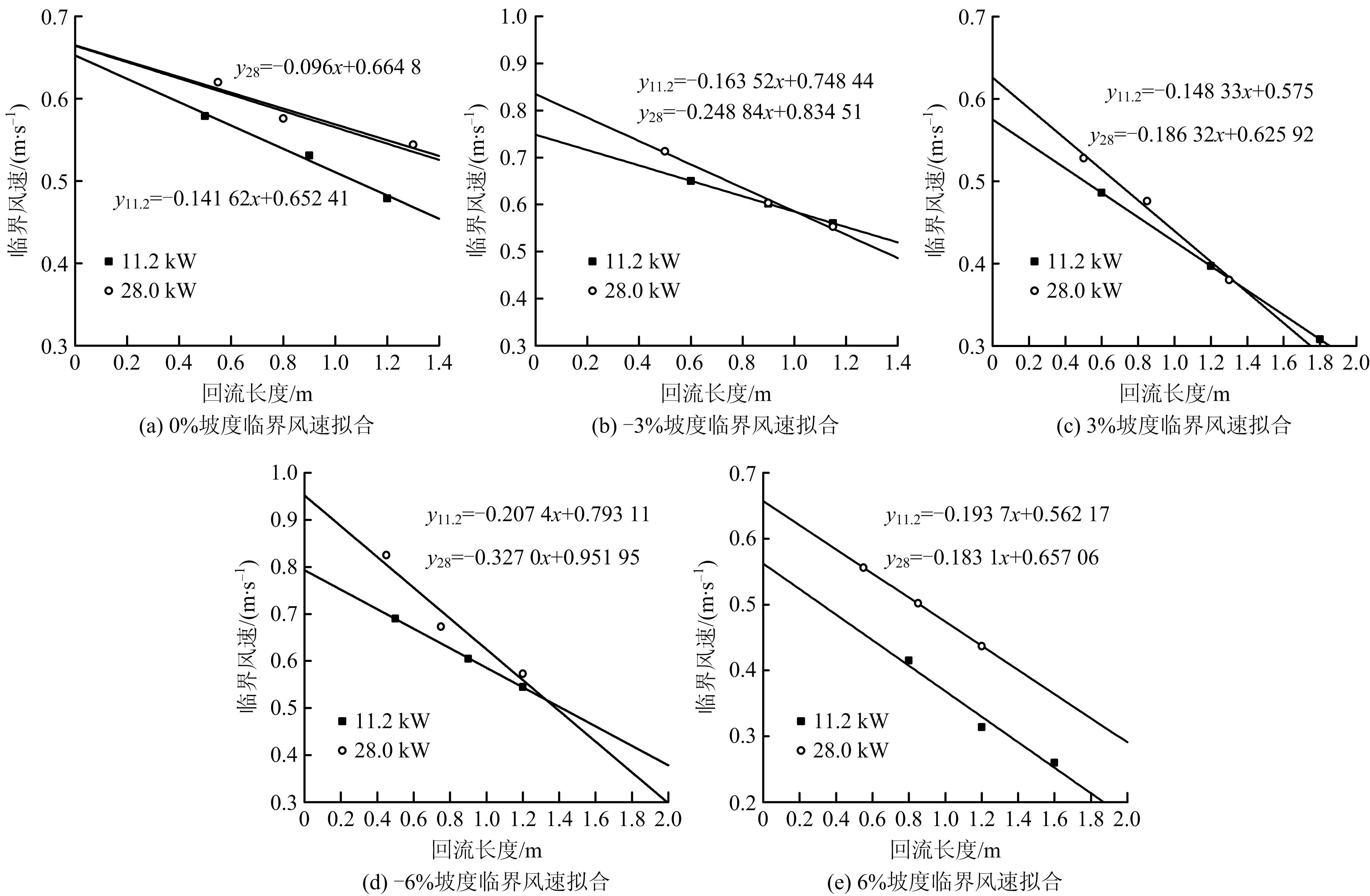
图4 不同坡度和火源功率条件下的临界风速Fig.4 Critical wind velocities under different slopes and fire source powers

如图5所示，0%坡度时，11.2 kW和28.0 kW的临界风速差别较小，分别为0.652 m/s和0.665 m/s；根据Wu和Bakar[10]的修正公式在本试验条件下计算出来的0%坡度的临界风速为0.596 m/s和0.689 m/s，其与本试验结果之间的误差分别为8.54%和3.58%。

图5 11.2，28.0 kW临界风速值Fig.5 Critical wind velocities of 11.2 kW and 28.0 kW

无送风时，由于坡度的存在，浮力效应加强，烟气向上坡方向蔓延速度加快。逆坡送风时，由于送风方向与烟气蔓延相反，阻碍烟气向上运动，因此临界风速相对0%坡度时更大，并且大功率火源产生烟气量大，临界风速更大。顺坡送风时，送风方向与烟气蔓延相同，加剧烟气向上运动，因此临界风速相对0%坡度时更小，并且在6%坡度时，临界风速与0%坡度几乎相同。

2.2 临界风速模型

Atkinson和Wu[8]提出坡度修正系数kg，考虑基于水平隧道临界风速的坡度与临界风速之间的关系，如式(1)所示：

(1)

式中：vc为有坡度隧道的临界风速值，m/s；vc0为水平隧道的临界风速值，m/s。

前人[8,11,13]大多采用逆坡送风的方式分析坡度与坡度修正系数之间的关系。表4为前人[8,11-13]得到的坡度修正系数kg和适用范围。Ko等[11]加入坡度修正系数，并通过研究得出了坡度为0°至-8°、火源功率为对应全尺寸16～28 MW的修正系数kg=1-0.033θ；Atkinson和Wu[8]通过研究得出了对应全尺寸15～75 MW火源功率在坡度为0°至-10°的修正系数kg=1-0.014θ；Yi等[12]同时研究了顺坡送风和逆坡送风，得出-3%至3%的修正系数，为kg=1-0.034s；另外，Li等[13]通过研究对应全尺寸火源功率5～20 MW，逆坡送风的修正系数，为kg=1-0.065s。

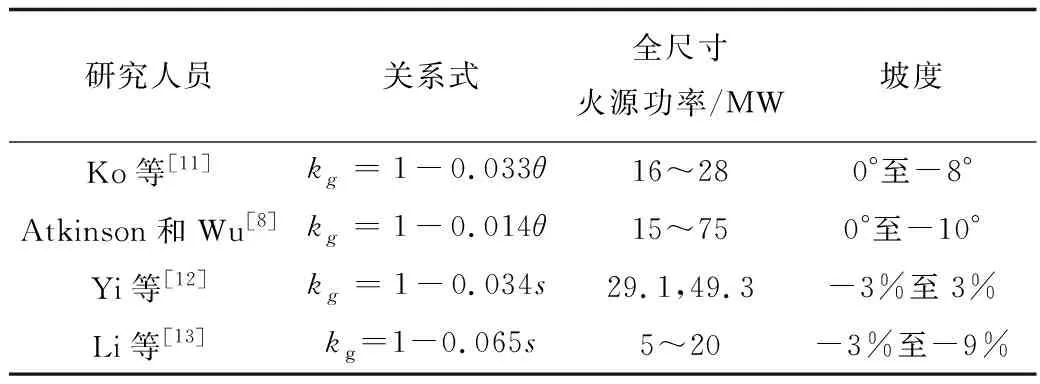
表4 kg与坡度之间的关系Table 4 Relationship between kg and slope

根据前人[8,11-13]研究结果，顺坡送风和逆坡送风的kg与坡度均呈线性关系。然而，本文试验研究发现，随着坡度增大，同一种火源功率的顺坡送风临界风速增速变缓，如图5所示。基于公式(1)对本文的试验数据进行拟合，kg与坡度关系如公式(2)所示，拟合结果与前人[8,11-13]的对比如图6所示。本文拟合出的曲线中，逆坡送风时与前人的研究结果基本吻合，逆坡送风的临界风速均与坡度成线性负相关。而顺坡送风时，与前人[8,11-13]的线性关系不同的是，本文试验得出的临界风速与坡度成反比例关系，即随着坡度增大，kg增速变缓。这是由于当坡度增大，烟气集聚减少，随着坡度从上坡方向迅速排出，烟气回流长度减小，坡度对回流长度的影响越来越小，随着坡度的增大，顺坡送风临界风速增速变缓，反映临界风速大小的kg减小速度也变缓。

(2)

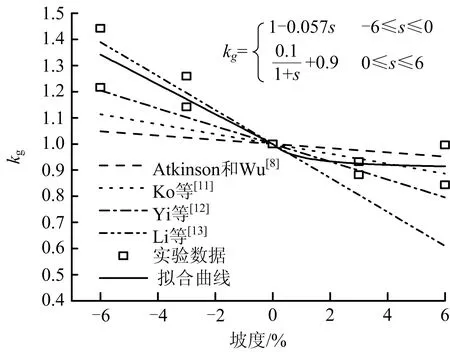
图6 不同模型下的坡度修正系数kgFig.6 Slope correction coefficient kg in different models

3 结论

1)通过缩尺模型，研究大火源功率(20，50 MW)不同坡度的试验，得到临界风速和其变化规律。

2)0%坡度时，11.2 kW和28.0 kW的临界风速相差不大；逆坡送风临界风速相对0%坡度时更大，顺坡送风临界风速相对0%坡度时更小；当火源功率足够大时，顺坡送风临界风速变化非常小。

3)根据试验结果，对前人的坡度与临界风速的预测模型进行修正，提出此次试验条件下的坡度修正系数。逆坡送风的临界风速与坡度为线性关系，顺坡送风的临界风速与坡度成反比例函数关系。