腹板开孔木工字梁受弯性能试验及有限元分析

熊亚荻，赵东晖，陈泓君，高 颖，孟鑫淼

（1.北京林业大学材料科学与技术学院 木材科学与工程北京市重点实验室 木质材料科学与应用教育部重点实验室，北京 100083；2.北京林业大学土木工程系，北京 100083）

与实心梁相比，木工字梁在承受相同荷载时，耗材更少、质量更轻、成本低且更易装卸，为满足美观及实用要求，对木工字梁的翼缘或腹板进行开孔来隐藏电线、通风或走水管道，可减少整体结构深度或提供更大的净空高度，优质的综合性能使木工字梁被广泛应用于建筑结构设计中[1-4]。

木工字梁由翼缘板、腹板和黏合剂3部分组成。翼缘板常用锯材（SL）、刨片层积材（LSL）或单板层积材（LVL）等材料制备，腹板常用材料为胶合板或定向刨花板（OSB），黏合剂黏结翼缘板与腹板[5]。开孔使得梁内的应力分布变得复杂，会降低其承载能力。国内外学者针对开孔位置、形状、尺寸和数量等条件，通过试验、理论计算及有限元模拟等方法，研究开孔木工字梁的力学性能[6-8]。木工字梁腹板受剪力较大，开孔后孔洞周围受力发生较大变化，更易发生破坏。Polocoser等[9]和Shahnewaz等[10]对单个圆孔木工字梁进行研究，结果表明木工字梁开孔后，腹板主要发生剪切破坏，工字梁脆性断裂。Afzal 等[11]、Lai[12]和Morrissey 等[5]研究发现腹 板 开孔率相同的条件下，由于角部应力集中，方形孔结构的承载力比圆孔下降较多。Jahromi 等[13]研究不同直径孔胶合板腹板工字梁的性能，发现开孔对工字梁整体刚度影响不大，但开孔尺寸越大，结构承载能力越低。Harte 等[14]研究蜂窝腹板工字梁的抗压特性，与同等尺寸的圆形或矩形开孔木工字梁相比，蜂窝孔有利于降低构件抗剪能力。

Morris 等[15]对轻型梁的剪切强度进行初步研究，包括带孔的OSB 腹板工字梁。Pirzada 等[16]基于机械原理设计了一种针对腹板带有单个圆孔的木质工字梁承载力的计算方法，模型预测和有限元模型吻合良好。有限元模拟也被广泛用于带有开孔的工字梁的数值计算中。Baylor 等[17]采用ANSYS 软件对腹板蜂窝开孔木工字梁进行有限元分析。Grandmont 等[18]采用ABAQUS 软件对木工字梁的力学性能进行敏感性分析，发现对结构力学性能影响最大的是腹板的面内剪切模量（G12）；St-Amour 等[19]采用同样方法发现影响最大的是受压翼缘的纵向弹性模量和扭转剪切模量。还有一些学者采用ABAQUS 软件建立不同的有限元模型。Guan 等[20]建立了具有单元移除功能的非线性三维有限元模型，Steensels 等[21]建立了梯度增强损伤模型，Zhu等[22]用户子程序进行建模，各研究分别对试验结果进行了很好的验证。

有关OSB 腹板圆孔开孔工字梁的研究还较少，且多为单圆孔开孔，而实际应用中，腹板需根据实际需要进行开孔。不同开孔数量和开孔位置下，工字梁受力性能的变化有较大差异，值得进一步研究。本研究选取长1.5 m，翼缘为LVL，腹板为OSB制成的木工字梁，进行开孔后力学性能研究，以开孔直径、开孔位置和开孔数量为变量，探究不同条件下木工字梁的破坏模式，研究腹板开孔对木工字梁结构整体力学性能的影响，通过有限元模拟分析孔边缘应力分布情况，对试验结果进行验证分析，以期为腹板开孔木工字梁的使用和优化提供依据，为实际施工中孔洞的合理布设提供参考。

1 材料与方法

1.1 材料

木工字梁由大连阔森特新型建材有限公司提供，型号为TJI210，长1.5 m，高356 mm；翼缘由LVL材料制成，截面尺寸为52 mm × 36 mm，依据GB∕T 15777-2017[23]得到的顺纹抗压强度为53.9 MPa，弹性模量为9.4 Gpa，翼缘板一侧开12 mm×9.5 mm 的凹槽，用来固定腹板；腹板材料为9.5 mm 厚的OSB板，依据GB∕T 15777-2017[23]、D7078∕D7078M⁃20[24]和GB∕T 1938-2009[25]得到的抗压强度、抗剪强度、抗拉强度和弹性模量的平均值分别为10.8、6.34、7.5 和3 451 MPa；翼缘和腹板用胶连接。

1.2 试件设计

将木工字梁腹板进行机械开孔（圆孔），探究不同开孔直径、数量和位置对木工字梁力学性能的影响。在梁长的五等分点、三等分点和跨中位置进行开孔，开孔数量分别为1、2 和4 个，孔径大小为90、130 和170 mm；设置1 个未开孔的试件作为对照（CK），共8 个试件（表1）。L 为孔心腹板边距（开孔圆心至腹板左边缘距离），D为孔径（图1）。

图1 试件截面示意图Fig.1 Section views of specimens(mm)

表1 试件参数Tab.1 Parameters of specimens

1.3 加载与量测

对试件进行三点弯曲试验，试件全长1 500 mm，支座间跨度为1 250 mm，在加载头与试件之间放置1 块钢垫板，避免上翼缘产生局部承压破坏。试验加载程序参考GB∕T 50329-2012[26]，通过邦威点液伺服加载系统施加竖向荷载。加载全程采用位移控制，加载速度为2 mm∕min，至承载力降至峰值荷载的80%时试验结束。正式加载前对试件进行预加载至2 kN，以确认仪器正常和消除系统误差。在试件跨中贴放5 个应变片（上下翼缘各1 个，腹板3个），开孔周围贴放4 个应变片，测量试件跨中及孔洞口周边应变值。同时，在试件跨中下部及两端支座对应的上翼缘板上端布置3 个位移计（LVDT），测量跨中挠度值和支座沉降值。试验中所测数据均由采集仪自动采集，采集频率10 Hz。为防止试件在加载过程中发生侧翻，在试件的两端分别添加防侧翻装置，用钢板进行约束，在钢板与试件之间涂抹润滑油，避免钢板与试件产生摩擦，影响试件力学性能的测量。试验加载装置、应变片和位移计布置如图2所示。

图2 位移计和应变片布置Fig.2 Layout of LVDT and strain gauges(mm)

2 结果与分析

2.1 试验现象与破坏模式

2.1.1 未开孔试件

试件W 为未开孔试件，加载初期，有微小的破坏声音，可能是木材表面的缺陷裂纹处受压产生的声音。随着荷载不断增加，木工字梁腹板初始缺陷部位发生顺纹劈裂，沿着与垂直方向夹角近45°劈裂，延续至下方小圆孔初始缺陷处（图3）。加载至极限荷载时，腹板发生剪切破坏彻底断裂，上翼缘和下翼缘与腹板接口分别被拉开；继续加载，腹板逐渐与翼板分离，试件完全破坏。无开孔木工字梁试验现象 与Afzal 等[11]、Pirzada 等[16]和Zhu 等[22]试验中的断裂破坏现象一致。

图3 试件W破坏现象Fig.3 Destruction phenomenon of specimen W

2.1.2 开孔直径对试件破坏程度的影响

试验加载过程中，随着开孔直径的增大，试件开孔周围应力集中的速率变快。至峰值荷载时，3个试件均在开孔右上角和左下角发生剪切破坏，开裂的两处位置点连线与加载方向呈45°夹角；孔的右下角和左上角均向前翘曲，破坏程度随开孔直径的增大而加剧；开孔上方腹板挤出上翼缘，下翼缘向支座方向滑移，上下翼缘虽然发生顺纹劈裂或层间开裂和翘曲，但均未断裂；试件S-300-170上翼缘的下侧在跨中部位向下翘曲（图4）。

2.1.3 开孔位置对试件破坏程度的影响

在高剪切区域，开单孔或不开孔试件均会发生腹板剪切破坏。开孔在三等分点（L=500 mm），开孔右上角和左下角连线与受力方向呈45°夹角处发生剪切破坏，随后剪切破坏发展至翼缘，导致翼缘与腹板间的接口松动；开孔在跨中位置（L=750 mm），开孔周围不易发生破坏；开孔在三等分点的破坏程度比在跨中位置严重，圆孔右上角、左上角和左下角均开裂，腹板和下翼缘的接口发生滑移（图5）。

图5 不同开孔位置试件的破坏现象Fig.5 Destruction phenomenon of specimens with holes in different positions

2.1.4 开孔数量对试件破坏程度的影响

破坏一致发生在高剪切区域；在远离加载头的开孔处，开孔周围发生与同位置开单孔试件类似的破坏现象。试件D-130 的破坏发生在右边开孔处，随着开孔右上角发生剪切破坏，右下角也受拉劈裂，并各自蔓延至上下翼缘，导致上下翼缘与腹板间开裂，上翼缘端头翘曲变形（图6a）。试件F-90的破坏发生在最左边的开孔处，右上角和左下角发生剪切破坏，左下角受拉劈裂，下翼缘端头翘曲变形（图6b）。

图6 不同开孔数量试件的破坏现象Fig.6 Destruction phenomenon of specimens with differ⁃ent hole numbers

2.2 荷载-跨中挠度曲线

弹性阶段内，所有试件在加载到一定程度时，均会产生开裂，荷载有小幅下降，刚度几乎保持不变；继续加载，荷载持续上升；至峰值荷载时，腹板发生剪切破坏；至第二峰值时，翼缘发生顺纹劈裂（图7）。对比4 组试件的荷载-跨中挠度曲线，在弹性阶段内，试件W、S-300-90 和S-300-130 的刚度接近，均高于试件S-300-170。4组试件都是脆性破坏，在达到峰值荷载前只有极少部分屈曲阶段。开孔试件的承载力较未开孔的有所降低；开孔直径越大，试件抗压能力越差，破坏时的峰值承载力越小。

图7 不同开孔直径试件荷载-跨中挠度曲线Fig.7 Load-mid-span deflection curves of specimens with different opening diameters

试件S-300-130 和S-750-130 的初始刚度均高于试件S-500-130，原因可能是靠近支座的五等分点开孔和跨中位置开孔抵抗变形的能力较强（图8）。跨中位置开孔的试件峰值荷载最高，可能是破坏发生在高剪切区域；试件未开孔的腹板上，没有应力重分布，可以承受较大的力，曲线趋势类似于无开孔试件。

图8 不同开孔位置试件荷载-跨中挠度曲线Fig.8 Load⁃mid⁃span deflection curves of specimens with holes in different positions

试件F-90 的初始刚度高于试件D-130，可能是因为试件F-90 的应力重分布较均匀，抵抗变形能力较强（图9）。试件F-90 只有跨中加载头下方的腹板被压坏，峰值荷载较开孔周围被破坏的试件D-130高。

图9 不同开孔数量试件荷载-跨中挠度曲线Fig.9 Load-mid⁃span deflection curves of specimens with different hole numbers

2.3 荷载-应变曲线

试件W 在加载过程中应变无剧烈变化，试件在25 kN 左右发生破坏（图10a）；S-750-130 试件的开孔周围也未发生破坏，应变片的应变在加载过程中无明显变化，曲线与图10a 相似。单开孔试件S-300-130、S-300-170 和S-500-130 的孔边应变变化与试件S-300-90 相似（图10b），加载头和支座连线位置为高剪切区域，所受应力较大，破坏发生时该方向的应变发生剧烈变化。多孔试件D-130 在跨中破坏严重，在右孔周围破坏剧烈（图10c ～ d），N1 受压应变数值很大。试件F-90 的4 个孔均未有明显剧烈破坏。

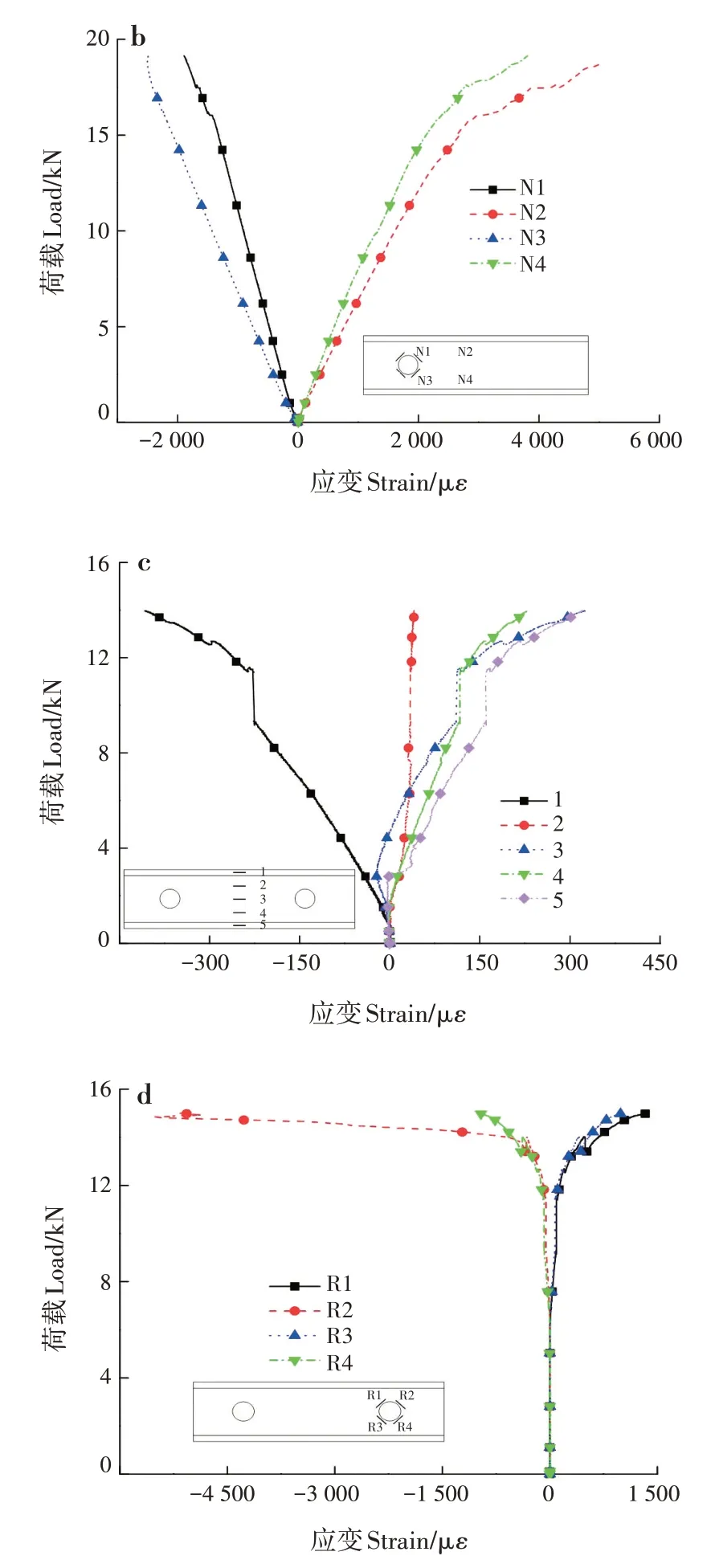
图10 不同试件典型荷载-应变曲线Fig.10 Typical load-strain curves of different specimens

2.4 峰值荷载

随着开孔直径的增大，试件在相同荷载下所承受的剪力变大，更容易破坏，因此峰值荷载下降。开孔直径由90 mm 增加至130 和170 mm 时，峰值荷载分别下降16.17%和29.43%；在开孔直径相同的情况下，开孔位置从跨中位置移到距离腹板边缘500 和300 mm 时，峰值荷载分别降低6.91% 和28.82%（图11）。随着开孔位置不断向靠近支座的高剪切区域移动，试件破坏发生在开孔周围，应力集中越明显，峰值荷载越小。对比开2 个孔和4 个孔试件，试件F-90 的峰值荷载较试件D-130 高28.23%，在开孔面积相近的条件下，开4个90 mm 孔比开2 个130 mm 孔更不易被破坏，试件承载能力更强。

图11 试件峰值荷载Fig.11 Peak loads of specimens

2.5 刚度

选取荷载位移曲线的弹性阶段经线性拟合得到刚度。刚度随开孔直径的增大而减小，当开孔直径从90 mm 增大至130 和170 mm 时，刚度分别下降1.23%和52.06%（图12）。130 mm 是可接受的开孔直径，170 mm 超过可接受范围。开孔位置不同时，开孔位于跨中位置的刚度较大。开孔面积相近的情况下，开4 个90 mm 孔比开两个130 mm 孔刚度大20.87%。

图12 试件刚度Fig.12 Stiffness of specimens

3 有限元数值模拟

3.1 模型及边界条件

采用ABAQUS 软件对木工字梁进行数值模拟。木材定义为各向异性材料，定义翼缘LVL 和腹板OSB 材料的主方向为Z 轴方向和Y 轴方向。翼缘LVL 和腹板OSB 材性参数如表2 所示[27]。边界条件为两个支座，分别只保留U3和UR1方向的自由度；单元类型选用实体单元，整体网格多为10 mm（图13）。翼缘和腹板的界面接触采用Cohesive黏结，Cohesive的3 个方向的刚度（Knn法向刚度、Kss剪切刚度和Ktt切向刚度）取0.10～0.31 N∕mm3[28]。加载过程为位移加载。

表2 木材翼缘和腹板的材性参数Tab.2 Mechanical properties of LVL and OSB

图13 试件有限元网格划分及边界条件Fig.13 Mesh and boundary conditions of finite element model

3.2 结果分析

有限元模拟结果与试验破坏现象和破坏模式一致。腹板在高剪切区域被拉坏或压坏，与无开孔试件腹板最先破坏的试验现象一致（图14a）；开孔直径为90、130 和170 mm 时，试件发生开孔周围腹板剪切破坏、腹板部分屈曲和翼缘端头腹板滑移，与试验现象一致（图14b ～ d）。在不同开孔位置和数量条件下，有限元分析也较为准确地模拟了试验破坏过程（图14e ～ h）。有限元模拟曲线和试验曲线吻合较好（图15）。对比有限元模拟刚度和试验所得刚度，有限元模拟结果较准确，刚度误差均在5%以内（表3）。

表3 模拟刚度与试验刚度Tab.3 Simulated and experimental stiffness

图14 试件剪应力云图Fig.14 Shear stress nephogram of specimens

图15 有限元模拟和试验荷载-跨中挠度曲线对比Fig.15 Comparison of load-mid-span deflection curves between finite element simulation(FE)and experiment(EXP)

4 结论

本研究对8根木工字梁开孔试件开展集中荷载作用下的弯曲试验，探究开孔直径、开孔位置和开孔数量对木工字梁破坏模式、刚度和承载力的影响，通过观察试验现象，分析破坏机理，建立较为准确的有限元模型。

集中荷载作用下，试件的破坏特征与开孔直径有关。随着开孔直径的增大，试件脆性破坏发展加快，最先破坏的位置是腹板开孔周围与加载方向呈45°角处。开孔位置不同时，破坏发生在高剪切区域，跨中位置开孔在腹板未开孔位置发生破坏，荷载跨中挠度曲线趋势与无开孔类似。开孔数量不同，破坏现象也不同，在靠近支座位置的开孔周围发生腹板剪切破坏。

随着开孔直径从90 mm 增大至130 和170 mm，木工字梁的峰值荷载分别下降16.17%和29.43%；在开孔直径相同的情况下，开孔位置从跨中位置移到距离腹板边缘300 和500 mm 时，木工字梁的峰值荷载分别下降28.82%和6.91%；在五等分点开4 个90 mm孔试件的峰值比在距离腹板边缘300 mm处两边各开1 个130 mm 孔高出28.23%。有限元模型中采用Cohesive行为模拟腹板翼缘板连接界面，其结果与试验结果吻合较好，刚度的模拟值与试验值的误差均小于5%。