考虑初始应力的大跨径钢箱梁斜拉桥自振特性分析

徐 韬， 王家豪， 张志程

(湖南省交通科学研究院有限公司， 湖南 长沙 410015)

0 引言

大跨径斜拉桥结构体系研究中，关于桥梁本身自振特性的分析至关重要，通过振动特性的分析可明确结构刚度分布，结构振型分析结果同时能为桥梁抗震和抗风设计提供指导，文献[1]研究了斜拉桥自振频率对抗震分析的影响，讨论了不同阶次振型模态下桥梁的振动特性；文献[2]以某斜拉-连续组合结构桥梁为研究对象，研究了结构静动力特性；文献[3]研究了矮塔斜拉桥的结构振动特性，并与常规斜拉桥自振频率进行了对比；文献[4]通过建立不同形式的有限元模型，对比分析了不同建模方法对结构振动频率求解的精度影响规律。但是在以往的实际工程中，模态分析往往仅考虑结构的线性特征，忽略了初始应力导致的结构非线性对振动特性的影响。本文以某大跨径钢箱梁斜拉桥为研究对象，计入结构初始应力的影响，对自振特性进行分析，相关研究成果可为斜拉桥动力学研究提供借鉴。

1 考虑初始应力的振动频率求解法

当结构自由振动时，其振动方程可描述为(不计阻尼项)：

(1)

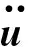
当结构以同一频率做简谐运动时，可表示为式(2)的形式。

{u}={φ}sin(ωt+θ)

(2)

式中：φ表示特征向量。

对于式(2)，等式两边分别求其一阶导数，并将其代入式(1)可得：

([K]-ω2[M]){φ}={0}

(3)

由式(3)可知，对于简谐运动的结构，其频率方程或特征方程为：

|[K]-ω2[M]|=0

(4)

在进行结构模态分析时，刚度矩阵[K]应计入应力刚度矩阵的影响，以便进行有初应力的模态分析。以大跨径斜拉桥这类柔性结构为例，在模态分析前首先应考虑计入结构恒载和活载效应导致的初应力影响。在ANSYS中，可通过(PSTRES，ON)命令对结构进行静力分析，获取结构的初应力矩阵，再对结构进行模态分析，此时结构的应力矩阵中已经包含了初应力矩阵。在进行模态分析时，在总体坐标系的6个方向上(3个平动方向和3个转动方向)施加单位位移激励荷载，以计算出各方向上的振型参与系数，通过求解该阶振型下的模态质量与振型参与系数的乘积可得到振型参与质量系数，通过振型参与质量系数即可判断振型数是否足够[5]。

2 工程概况及有限元模拟

以湖南南益高速胜天大桥为研究对象，该桥结构形式为半漂浮体系，采用双塔双索面布置，主桥跨径组合为(182+450+182)m，横截面为扁平钢箱梁，材料标号为Q345，桥面全宽30.5 m。纵桥向共分为68对扣索，索间标准间距为12 m，加密区索距5 m，斜拉索采用高强度低松弛预应力钢绞线，钢箱梁采用吊装焊接施工。索塔位置支座为竖向支座和横向抗风支座，纵桥向设置粘滞阻尼器2个。桥型立面布置见图1。

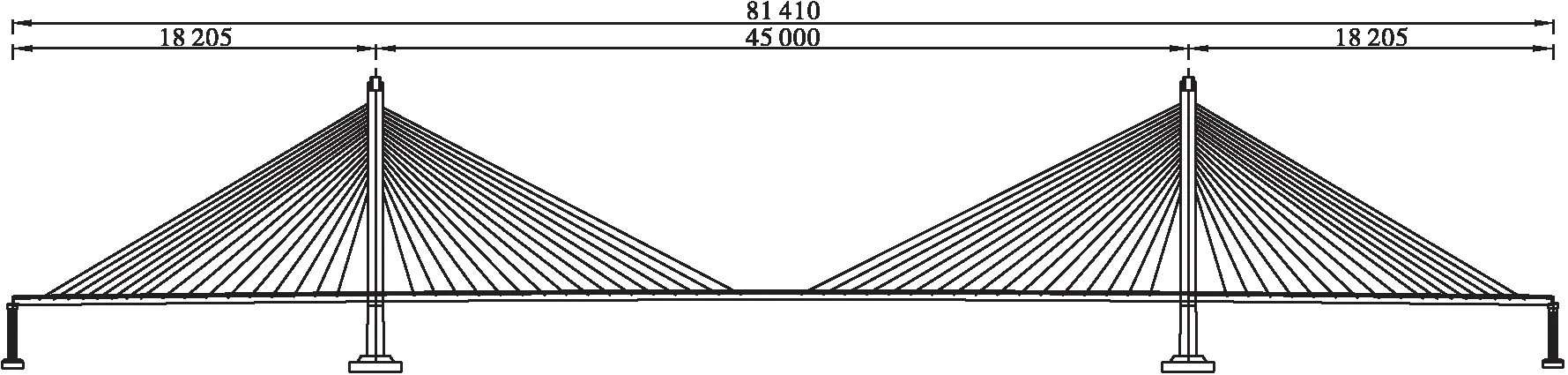
图1 南益高速胜天大桥桥型立面布置(单位： cm)

在斜拉桥有限元模拟时，采用“鱼骨法”模拟钢箱梁主梁部分，主梁使用Beam188建模，横向联系采用MPC184刚性梁模拟，斜拉索采用Link10杆单元模拟，梁杆单元按共节点处理，斜拉索索力采用实常数法输入，使用垂度公式计入弹性模量修正的影响。为简化计算，不考虑桥面系的刚度贡献，以Mass21质量单元考虑其质量的影响，根据桥梁图纸施加约束条件，有限元模型及边界条件见表1和图2。

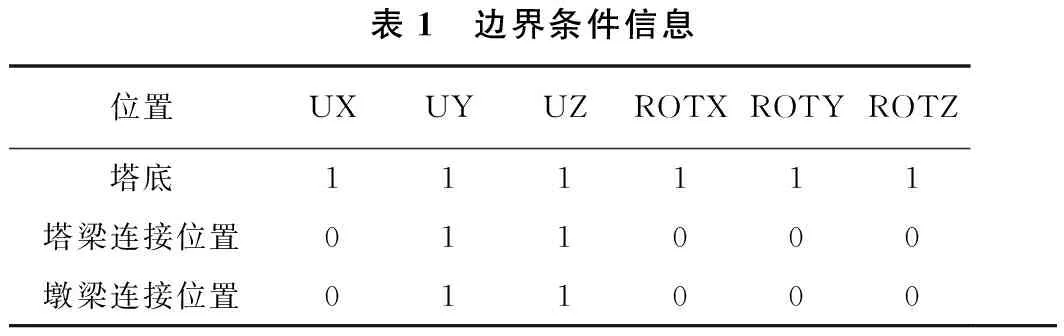
表1 边界条件信息位置UXUYUZROTXROTYROTZ塔底111111塔梁连接位置011000墩梁连接位置011000

图2 斜拉桥有限元模型

斜拉索初始索力使用初应变法模拟，调用ANSYS中单元生死功能模拟斜拉桥施工过程，根据上述方法，首先对该斜拉桥进行线弹性静力分析，在静力分析时保存初始应力刚度矩阵，然后在模态分析时计入该初始应力刚度矩阵的影响。

3 有限元计算结果

使用Block Lanczos法获取结构前100阶频率及前10阶振型计算结果，并计算其振型参与质量以验证所取振型数是否满足要求。一般认为，使用多振型反应谱法进行模态计算时，应使得所考虑的振型阶数在计算方向上获得90%以上的有效质量。为满足抗震分析对模态的精度要求(有效参与质量达90%以上)，本文提取前100阶次模态振型参与质量系数计算结果。计算结果表明：对于该桥，取前100阶模态时，其振型参与质量系数基本达到了100%，计算精度满足要求，具体结果见表2。

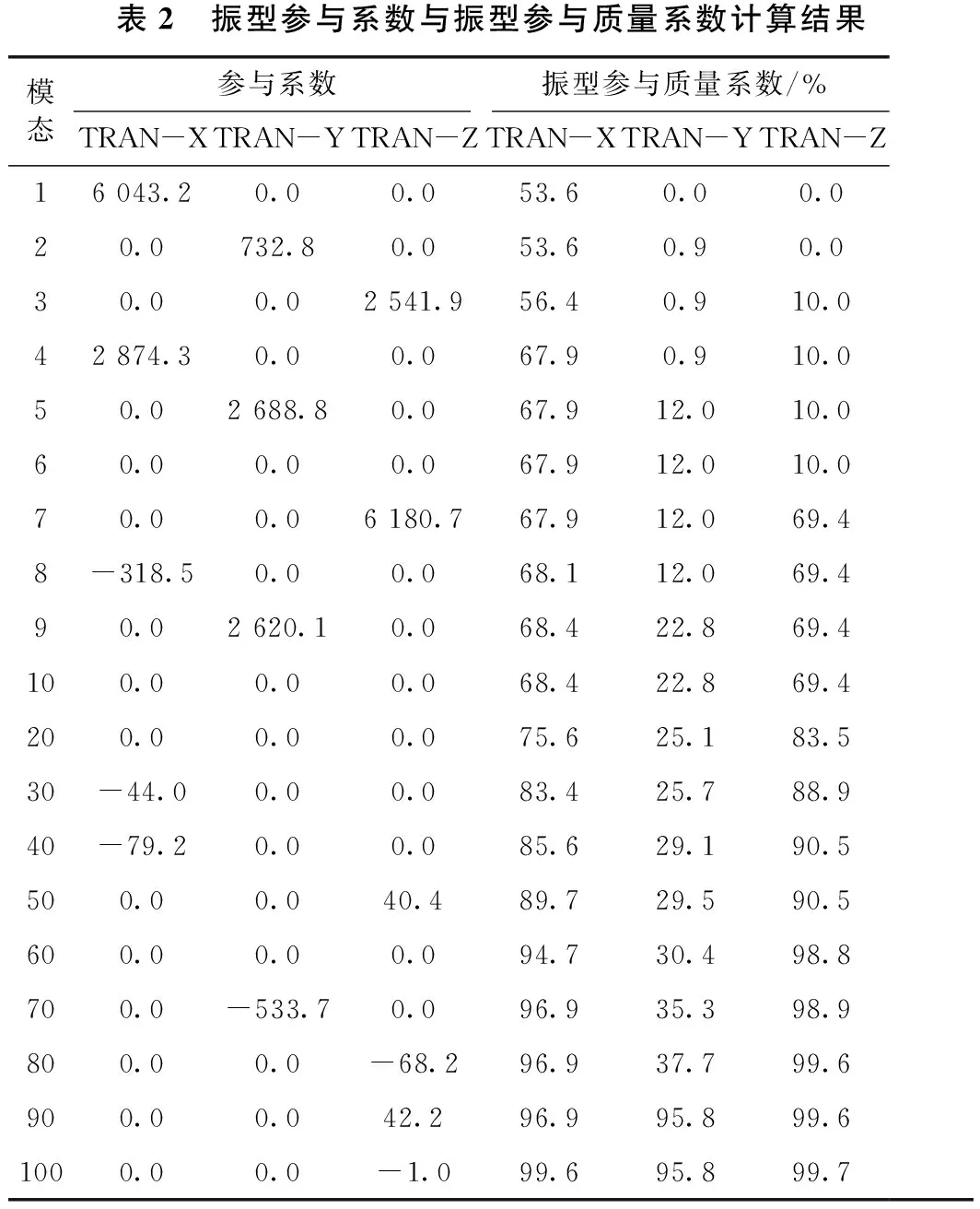
表2 振型参与系数与振型参与质量系数计算结果模态参与系数振型参与质量系数/%TRAN-XTRAN-YTRAN-ZTRAN-XTRAN-YTRAN-Z16 043.20.00.053.60.00.020.0732.80.053.60.90.030.00.02 541.956.40.910.042 874.30.00.067.90.910.050.02 688.80.067.912.010.060.00.00.067.912.010.070.00.06 180.767.912.069.48-318.50.00.068.112.069.490.02 620.10.068.422.869.4100.00.00.068.422.869.4200.00.00.075.625.183.530-44.00.00.083.425.788.940-79.20.00.085.629.190.5500.00.040.489.729.590.5600.00.00.094.730.498.8700.0-533.70.096.935.398.9800.00.0-68.296.937.799.6900.00.042.296.995.899.61000.00.0-1.099.695.899.7

表3为斜拉桥振动频率对比。表3给出了考虑初始应力与不考虑初始应力两种情况下斜拉桥前100阶部分阶次振动频率计算结果，计算结果表明：当斜拉桥呈低阶次模态时(1～10阶次模态)，两者结果相差较小，振动频率相差幅度均在5%以内，当模态阶次逐渐升高时，两者相差幅度也随之增大；模态从第20阶升至第100阶时，相差幅度从6.45%增大至13.98%，因此在进行斜拉桥高阶模态分析时，由结构初应力导致的非线性行为不能忽略。同时从表3还可以看出，无论考虑初应力与否，斜拉桥在低阶模态时其振动频率均较小，振动频率分布密集，极易造成相邻阶次模态振型相互干扰，为结构动力学分析带来困难。

表3 斜拉桥振动频率对比模态号计入初始应力/Hz不计入初始应力/Hz差值幅度/%10.173 20.181 4-4.5220.304 80.320 6-4.9330.383 20.401 7-4.6140.397 10.413 4-5.2550.487 80.509 2-4.2060.563 60.586 3-3.8770.569 60.598 7-4.8680.698 50.721 3-3.1690.700 40.735 2-4.73100.752 20.778 9-3.43201.299 11.388 7-6.45302.107 22.276 8-7.45402.790 73.024 3-7.72503.714 54.068 5-8.70604.628 25.085 5-8.99705.668 16.237 4-9.13806.372 67.157 6-10.97907.7838.869 5-12.251008.705 410.119 7-13.98

表4及图3给出了斜拉桥部分阶次振型计算结果，由计算结果可知：考虑初应力后该桥振型与常规模态分析时振型基本一致。但根据图3给出的振型计算结果，对于低阶次振动模态，其振型往往不是唯一的，在某个阶次的振动模态中往往包含了多个振型，呈现出较为明显的三维耦合特性，如该桥1阶振动时，主要振型为主梁纵飘，但同时存在主梁竖向弯曲的振型，这是由于斜拉桥低阶模态下频率分布密集，相近阶次模态振型相互干扰造成的，为简化计算分析流程，一般取占主要成分的振型即可。

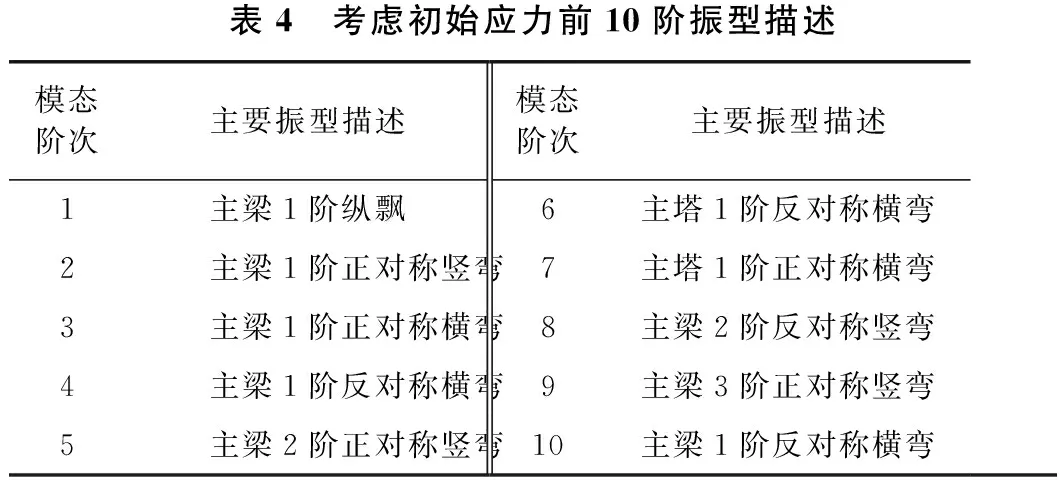
表4 考虑初始应力前10阶振型描述模态阶次主要振型描述模态阶次主要振型描述1主梁1阶纵飘6主塔1阶反对称横弯2主梁1阶正对称竖弯7主塔1阶正对称横弯3主梁1阶正对称横弯8主梁2阶反对称竖弯4主梁1阶反对称横弯9主梁3阶正对称竖弯5主梁2阶正对称竖弯10主梁1阶反对称横弯

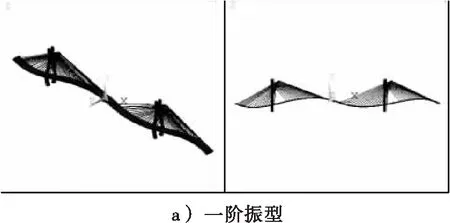
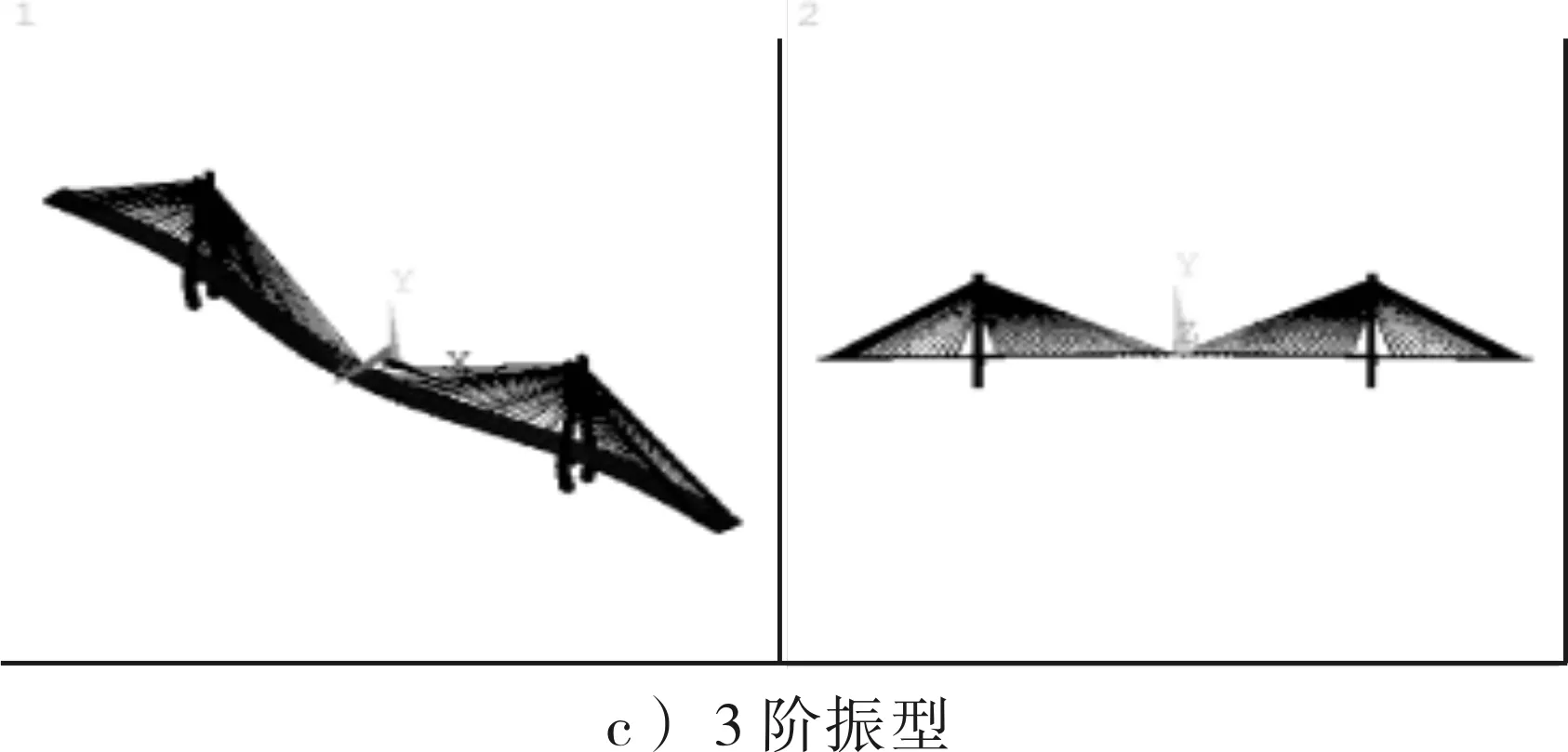
图3 前6阶振型计算结果

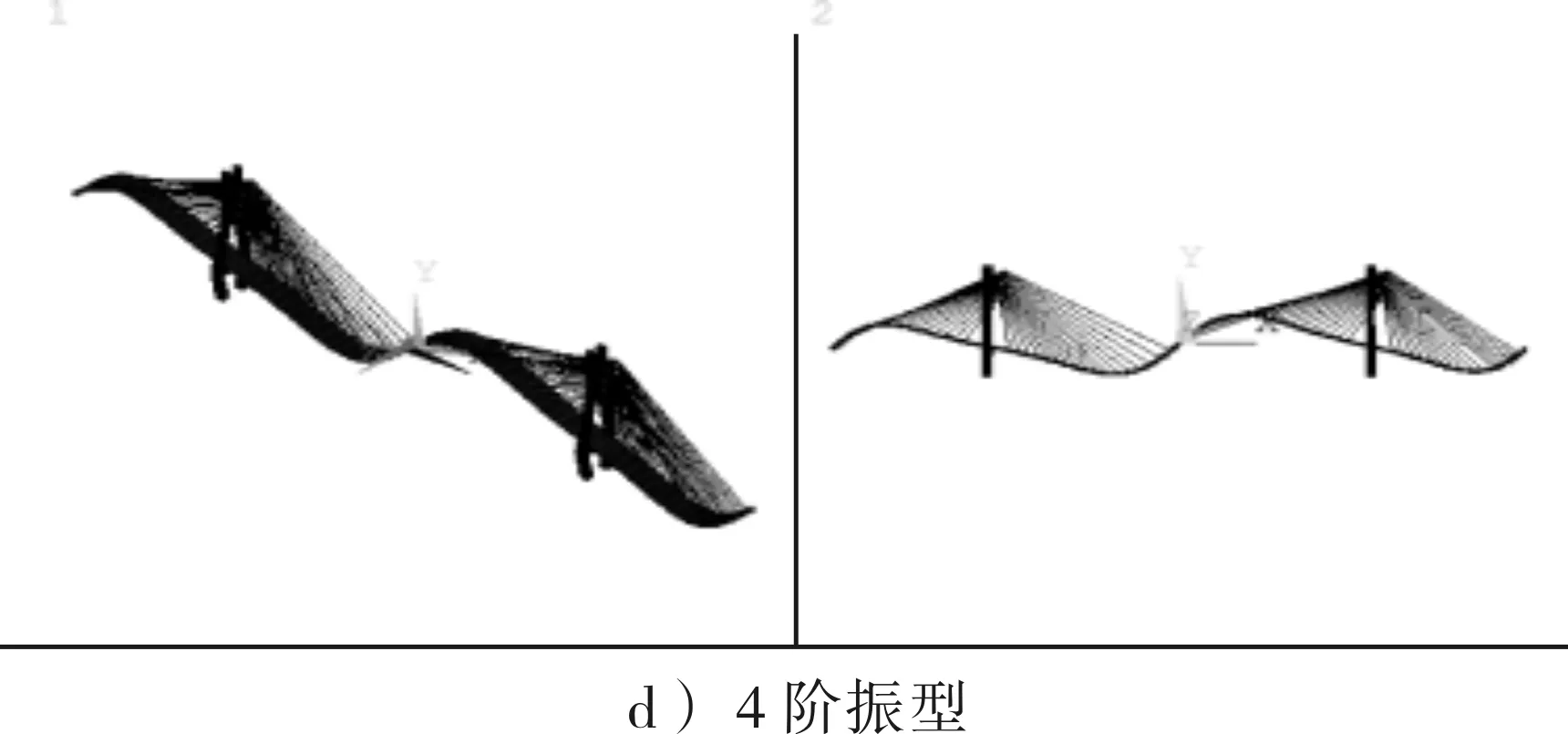
续图3 前6阶振型计算结果

4 结论

以某大跨径钢箱梁斜拉桥为研究对象，建立了该桥ANSYS有限元模型，考虑了结构初始应力的非线性影响效应，对该桥开展了振动特性研究工作，可得到以下结论：

1)斜拉桥在低阶振动时，振动频率低、周期长，模态成分复杂，呈现出典型的三维耦合特性，相邻模态振型容易形成相互干扰。

2)当计入结构初始应力的影响后，以该桥为例，结构低阶模态下(1～10阶次)振动频率与不计入初始应力时相差不大，差值幅度均在5%以内，但对于高阶模态(20～100阶次)，两者振动频率之间相差较为明显，且差值幅度与模态阶次基本呈正相关，在100阶次时振动频率相差了13.98%。因此在斜拉桥高阶次振动分析时，应计入初始应力的影响。