行波激励下大跨越输电线路纵向地震响应分析

杨军永，朱从民，朱瑞元

(1.国网山东省电力公司莱芜供电公司，济南271100；2.电力规划总院有限公司，北京100120)

0 引言

输电线路是生命线工程的重要组成部分，一旦遭到地震破坏，将对社会、经济和人民生活造成严重影响。受地形、地貌、交通、土地等各种因素影响，线路路径选择受限，不可避免穿越地震多发地带。历次地震中，输电线路均遭受了不同程度的破坏，如1994年美国Northridge地震造成当地63条输电线路破坏，其中230 kV和500 kV线路震害最为突出[1]。1995年日本神户地震造成20多条线路破坏[2]。1999年台湾省集集地震中，345 kV超高压输电线路受损28条，造成整个台湾省北部的电力供应在震后1星期仍不能正常工作[3-4]。2008年汶川地震中110 kV输电线路停运122条，220 kV输电线路停运63条[5]。2013年芦山地震中35 kV以上输电线路有224条停运，芦山、天全、宝兴三县电网全部垮网[6]。2017年九寨沟地震造成了阿坝区35 kV与110 kV输电线路停运[7]。随着电网建设不断扩展，提高输电线路抗震性能对于保障电力安全稳定有着至关重要的意义。

以往的输电线路设计中对风、冰及导地线张力荷载的研究比较深入，设计对策较为成熟。近年来，国内外学者对输电线路地震灾害开展了一系列研究，对地震灾害的认识正在逐步提升。文献[8-11]在理论模型方面，提出了串联多质点等效梁模型、多质点模型和等效刚度理论简化模型等；文献[12-14]在有限元模拟方面，开展了输电塔单塔、塔线体系、多维多点输入等多方面的地震响应分析；文献[15-18]探索开展了简化模型和缩尺模型的振动台试验。总体而言，以往研究对输电线路体系在进行了较多简化考虑，对特殊地形引起的大档距、大高差等情况考虑较少。

为了更加深入理解地震动多点输入下大高差、大档距塔线耦合体系的响应，尽可能模拟真实的地震响应情况，本文选取某±500 kV直流输电线路一个高差较大的大跨越段，建立了精细化的“四塔三线”有限元模型，开展了一致激励与非一致激励地震动模拟分析研究。

1 研究对象及模型建立

1.1 工程背景

以某±500 kV直流输电线路大跨越为案例进行分析研究。该大跨越耐张段全长2 759 m，采用不等跨的“耐-直-直-耐”跨越方式，从左往右三跨档距分别为703 m、1 053 m、1 003 m，连续大档距为本文研究对象的一个特点。其中中间两基直线跨越塔总高87.95 m，呼高78 m，塔身主材采用Q420级钢管，塔头及导地线支架采用Q235和Q345级角钢；左端和右端的耐张锚塔总高37.8 m，呼高 26 m，采用Q345级和Q235级角钢，具体塔型如图1所示。导线和地线分别采用4×AACSR/EST-450/200和LBGJ-240-20AC钢芯铝绞线。

图1 铁塔外形图

另外如图2所示，两侧锚塔与中间的跨越塔塔位存在较显著的海拔高差，其中中间两基直线塔海拔一致，为最低；左端锚塔塔位海拔较之高出96 m，右端锚塔塔位海拔较之高出29.5 m。大高差是本文研究对象的另一特点。

图2 塔线体系有限元模型

1.2 计算模型

对于输电塔线体系这种耦合性显著的系统，导地线对输电塔振动响应的影响程度与两侧档距大小、相邻铁塔的高差大小有关，本文针对该大跨越耐张段建立了精细化的“四塔三线”有限元模型。其中，跨越塔和锚塔所有杆件均采用梁单元进行模拟，端部按固定约束考虑；其中跨越塔塔腿主材规格为D402×12，锚塔塔腿主材规格为2L160×16，Q420、Q345和Q235钢的屈服强度分别取400 MPa、310 MPa和215 MPa，弹性模量统一取2.06×105MPa，泊松比按0.3考虑。绝缘子串采用刚性杆单元进行模拟，考虑端部转动效应。导线和地线为柔性悬索，其形状是由边界条件、张力和均布的重力荷载共同决定的，本次采用索单元进行模拟，初始几何形状由抛物线法给出，通过索单元的初始应变来设定导地线张力，然后施加重力荷载，通过反复的非线性迭代找到最终形状，以达到导地线张力平衡状态；其中导线AACSR/EST-450/200自重2.966 kg/m，直径33.3 mm，弹性模量9.71×104MPa；地线LBGJ-240-20AC自重1.596 kg/m，直径20 mm，弹性模量1.47×105MPa。需要注意的是，考虑到耐张锚塔本身设计时考虑了单侧断线工况，刚度足够大，“四塔三线”有限元模型中耐张锚塔的地线支架和导线横担外侧未考虑常规线路导地线约束。

2 地震响应分析方法

2.1 模态分析

在进行塔线体系分析之前，首先开展了跨越塔和锚塔的单塔模态分析，结果显示，跨越塔前两阶模态振型分别为垂直导线方向和顺导线方向弯曲变形，对应频率分别为1.23 Hz和1.25 Hz；锚塔自身刚度比较大，前两阶模态频率较大，垂直导线方向和顺导线方向分别为3.45 Hz和3.63 Hz。随后的“四塔三线”塔线体系模态分析中，前600阶模态频率在0.02～2.21 Hz之间，大部分的模态振型为导地线的振型。如图3所示，塔线体系中，直线塔在垂直导线方向和顺导线方向的第一阶频率分别降为0.84 Hz和0.97 Hz，导地线给铁塔带来的附加垂重以及柔性摆动，使得跨越塔固有频率显著降低，避开了地震动卓越频率范围1 Hz～10 Hz；虽然塔线体系下的锚塔固有频率变化规律类似，但考虑到“四塔三线”塔线体系无法准确考虑锚塔的边界条件，锚塔在塔线体系中的固有频率具体结果不予讨论。

图3 跨越塔在塔线体系中的前两阶振型

2.2 地震分析方法

大跨越耐张段的三跨档距较大，四基铁塔所处塔位的地震动必然存在着差异，需要采用非一致激励模拟四基铁塔的地震输入。本文采取简化处理方法，采用行波激励(给定视波速)来考虑地震波到达不同铁塔的时间差异。塔线体系在非一致激励下的运动方程为：

(1)

与风致振动阻尼机理略有不同，地震作用下塔线体系的阻尼主要来源于材料本身、连接构造，其中连接构造阻尼极其复杂。本文从实用的角度出发，采用Rayleigh阻尼模型简化计算，根据塔线体系的模态分析结果和钢结构常用阻尼比0.02，近似得出结构的Rayleigh阻尼常数α=0.295 0，β=0.008 5。

2.3 地震波选用

该±500 kV直流输电线路大跨越位于7度抗震设防区域，场地反应谱特征周期0.4 s。本文选取Elcentro波(0.4～0.5 s)、Taft波(0.3～0.4 s)[19]，另外根据场地条件生成1条人工波。输入地震动峰值按照7度罕遇地震考虑，统一调整为2.2 m/s2。当前设计规范中尚无视波速取值规定，且不具备文献[20]所需详细地勘资料，本文暂按2 000 m/s、4 000 m/s考虑。根据以往研究，塔线体系横向振动机理较简单，接近与铁塔与质量摆的组合，本文设定输入方向为纵向，重点研究顺线路方向响应规律。图4—5分别给出人工波的加速度时程和反应谱。

图4 人工波加速度时程

图5 人工波反应谱

3 地震响应结果分析

由于“四塔三线”塔线体系无法准确考虑锚塔的边界条件，锚塔在塔线体系中的地震响应结果并不准确，本文仅分析跨越塔及跨越档导线的响应。

3.1 模态分析

如表1—2所示，跨越塔塔顶位移峰值最大为0.097 m，显著小于长期荷载工况下的设计限值(3h/1 000，h为测点高度)[21]。从地震响应机理分析可知，与风荷载的施加方式不一样，地震动直接激励输电塔底部，通过塔身向上传导，导地线受地震激励比较小且自身阻尼耗能作用大，因此导地线对跨越塔位移起到约束作用，而非放大作用。

表1 左侧跨越塔顶部位移

表2 右侧跨越塔顶部位移

行波效应对跨越塔的位移响应有一定的影响，但影响大小与地震波、视波速和塔位等各因素有关，没有明显规律可循，如同样输入Elcentro波和人工波，左侧跨越塔在视波速2 000 m/s下的顶部位移大于视波速4 000 m/s下的顶部位移，右侧跨越塔的规律则相反。

分析同一地震动激励下跨越塔塔顶位移时程曲线，一致激励和行波激励下的变化规律较为明确。如图6—8所示，视波速4 000 m/s下的位移时程曲线形状接近一致激励时的位移时程曲线，因为视波速过大，铁塔间地震激励接近同步；相比之下，视波速2 000 m/s下的位移时程曲线衰减速度快，因为铁塔间地震激励不同步对铁塔位移衰减是有利的。

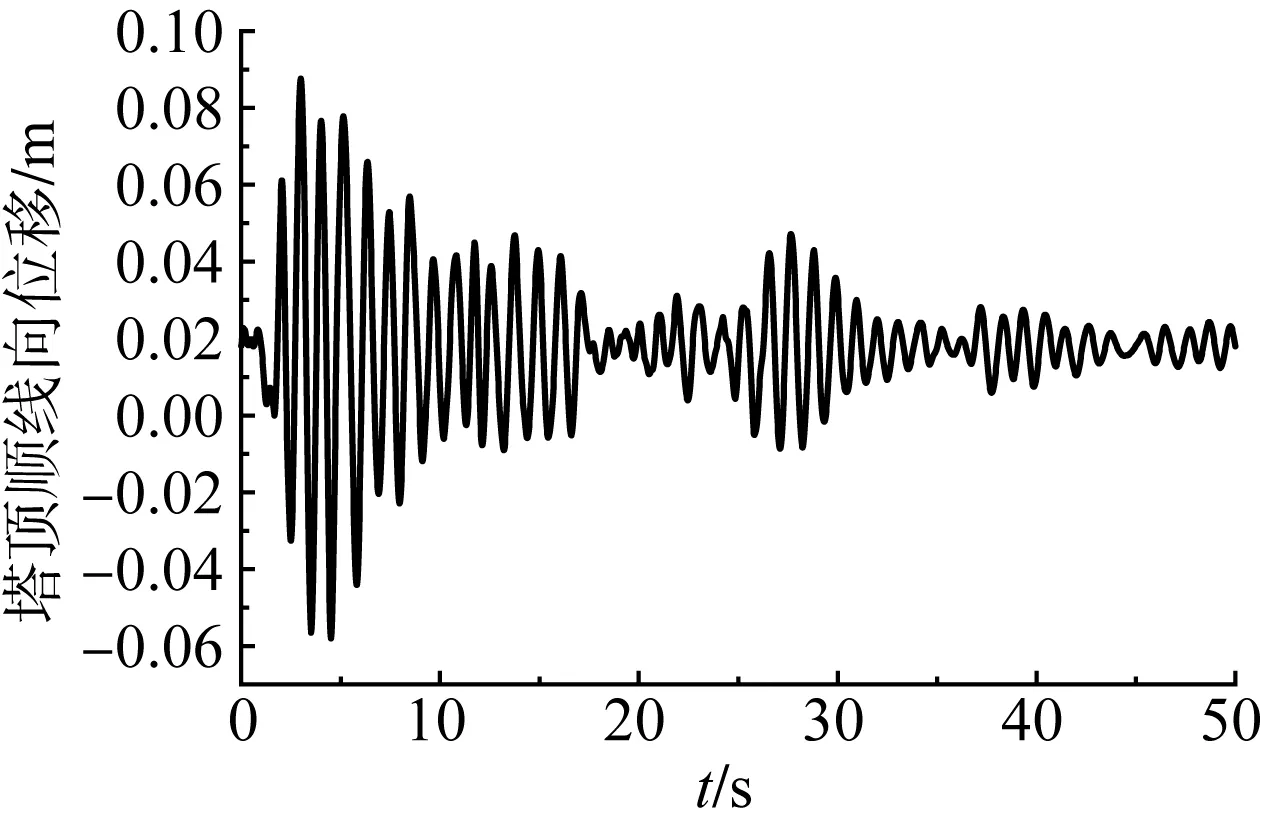
图6 一致激励下左侧跨越塔塔顶位移时程曲线

图7 行波激励下(2 000 m/s)左侧跨越塔塔顶位移时程曲线

图8 行波激励下(4 000 m/s)左侧跨越塔塔顶位移时程曲线

3.2 杆件应力

根据以往的研究经验，地震动激励下导地线重力、张力是铁塔的主要外负荷，轴向应力最容易超限的杆件往往分布在塔头。本文根据跨越塔塔头构造型式，选取4根杆件作为应力观测位置，杆件1—3为地线支架和横担主材，杆件4为塔身主材，具体位置如图9所示。

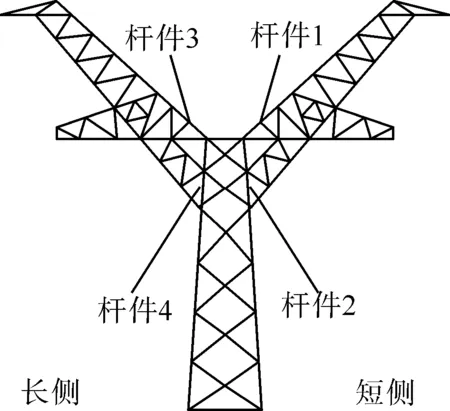
图9 杆件应力观测位置

表3和表4对不同地震动下左右两侧跨越塔的杆件应力峰值取均值。在7度罕遇地震下，杆件1—杆件3应力峰值最大350.95 MPa，为材料屈服强度(Q420)的90%；杆件4应力峰值最大215.76 MPa，为材料屈服强度(Q345)的70%；4根杆件均处于弹性阶段。此外，一致激励和行波激励下4根杆件应力峰值基本一致。

表3 左侧跨越塔杆件应力峰值

表4 右侧跨越塔杆件应力峰值

分析杆件1～4在不同地震动激励下的应力时程曲线得知，4根杆件的应力时程曲线变化规律基本一致，振幅在1.5 s后趋于稳定，应力稳定值与地震动激励前的应力初值基本一致。图10给出左侧跨越塔杆件1在Elcentro波一致激励下的应力时程。

图10 Elcentro波一致激励左侧跨越塔杆件1应力时程

3.3 跨越档导线张力

锚塔采用不等长横担，两侧横担在塔身外侧尺寸分别为10.81 m和7.31 m，本文据此将跨越档导线按长侧和短侧编号，如图11所示。表5对不同地震动下的导线张力峰值取均值。两侧导线最大值369.05 kN虽然小于导线拉断力456.89 kN，但是远高于设计限值(40%拉断力)[22]，两侧导线的张力峰值几乎不受行波激励影响。此外，长侧导线张力峰值小于短侧导线的张力峰值，意味着两侧导线张力相对大小与锚塔两侧横担长度具有一定相关性。

图11 跨越档导线

表5 跨越档导线张力峰值

4 结论

本文针对具有大档距和大高差的某±500 kV直流输电线路大跨越工程进行了模态分析和纵向地震动激励下的动力时程分析，并将一致激励和行波激励下地震动相应进行分析，得出结论如下。

1)跨越塔单塔在横线路方向、顺线路方向固有频率在1.23 Hz以上，而在塔线体系中降至0.97 Hz以下，导地线作用使得铁塔在地震波卓越频率范围内不易发生类共振。

2)跨越塔塔顶位移峰值最大为0.097 m，显著小于长期荷载工况下的设计限值。跨越塔塔顶位移受行波激励的影响，但是没有明显的规律可循。

3)地线支架和横担主材应力峰值为材料屈服强度的90%，塔身主材应力峰值为材料屈服强度70%，均在弹性应力范围内，且受行波激励影响较小。

4)导线张力峰值远高于张力设计值，但仍小于拉断力。导线张力几乎不受行波激励的影响，只与锚塔两侧横担长度具有一定相关性。

5)地震波样本较少、视波速准确性有待研究等因素对规律性结论有一定影响，下一步有必要研究准确估计实际场地条件下的视波速，并开展多个实测地震波样本下的模拟分析。

6)“四塔三线”模型中无法准确考虑耐张锚塔外侧边界条件，本文只能对跨越塔地震响应进行分析，在工程数据等条件允许的情况下有必要进一步开展2～3个耐张段的模拟分析，对锚塔的地震动响应进行分析研究。