短试验段内格栅湍流场风洞试验研究

杨俊伟，杨 华，付士凤，宗旺旺，沙成龙

1.扬州大学 电气与能源动力工程学院，江苏 扬州 225147；2.扬州大学 广陵学院，江苏 扬州 225000

0 引 言

在风洞试验中，设置格栅是模拟湍流风环境最常见的手段。风力机、涡轮叶片等在实际运行中湍流强度较高（约为5%～25%），基于较低湍流强度工况研究得到的结论与真实环境存在差异，因此需在风洞中通过设置格栅得到均匀的高湍流场[1-3]。针对此类格栅后方流场特性的研究，自Simmons 和Salter[4]通过格栅制造湍流场以来一直持续至今。由于格栅对来流的阻碍和扰动，会使流动不稳定，形成多个小旋涡，流线杂乱，层流演变为湍流。Mohamed 和Larue[5]指出格栅湍流场后方存在2 个区域，即以湍流衰减为主要特征的远场区域和受格栅几何参数影响强烈的近场区域。现有的湍流特性研究大都是通过风洞试验调制出湍流场，分析湍流参数变化规律等问题。但这些研究主要集中在流动充分发展的远场区域。Kitamura 等[6]认为格栅湍流沿轴向衰减幂率约为–1.2。Lysak 等[7]测得轴向衰减幂率约为–1.3。国内学者中，白桦等[8]通过调整格栅间距和格栅宽度，拟合轴向3.5 m 处湍流参数经验公式，表明湍流强度受格栅宽度影响较大；严磊[9]和袁星[10]等对湍流参数沿风洞轴向变化规律进行研究，调制出相应的湍流场。目前，对格栅后方近场区域的研究相对较少。由于格栅的离散布置且格栅下游距离不足，因此较短轴向距离处的流场存在一定程度的各向异性[11]。Vita 等[12]结合风洞膨胀试验段分析了格栅下游湍流特性变化规律；Shao 等[13]在水洞中分析了养殖网箱近尾流区的流场特性，发现当轴向距离与格栅条尺寸比值为4～10 时，湍流强度呈指数衰变。Yasuda 等[14]通过数值模拟方法，得到近场区域功率密度谱和压力谱的幂率分别为–1.7 和–2.3。

综上所述，为在短试验段风洞中模拟高湍流场，进行风力机试验，本文设计了2 种方型格栅和3 种竖条格栅，并利用热线风速仪进行流场测量。结合试验数据及格栅几何参数，对比分析湍流参数的规律，拟合近场区域的经验公式，为在轴向距离较短的风洞中布置湍流场提供参考。

1 试验装置与方法

1.1 格栅设计

一般而言，格栅的设计需考虑3 个参数：栅条宽度H、相邻栅条间隔宽度M和格栅与测点距离（后文简称：格栅距离）x。对比现有的几类格栅经验公式，文献[5，8，12]分别提出了顺风向湍流强度Iu的经验公式：

其中，A 为经验常数，取值与格栅几何参数相关；n为轴向衰变指数；为测试截面平均来流风速。

式（2）为M=30 cm、x=3.5 m 时格栅宽度H与顺风向湍流强度的关系式。

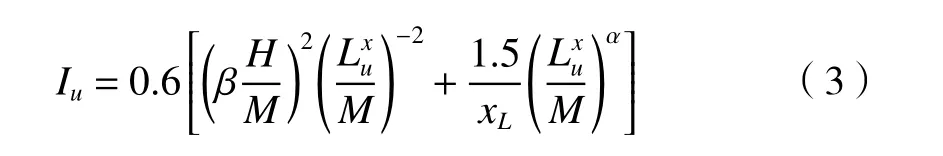
其中，α为截面出入口面积之比；Lux为顺风向平均湍流积分尺度；扩展距离xL=4/M；β为网格孔隙率。

从经验公式来看，式（1）中经验常数A 的取值依赖于格栅的初始条件，轴向衰变指数n需要通过大量实测数据拟合；式（2）仅适用于格栅后方x=3.5 m处的截面；式（3）所用参数较多。为进一步减少前期的调试工作，在短的轴向距离内调制出不同特性的湍流场，本文在扬州大学回流式低速风洞内进行试验，试验段的长、宽、高分别为3.0 m、3.0 m、1.5 m。试验段入口配有蜂窝器和3 层细格栅，使来流湍流强度较低（0.2%）。格栅采用常见的3 cm×3 cm 截面铝制型材组装，共5 个布置方案，如图1（a）～（e）所示。方案1、4 为方型格栅，方案2、3、5 为竖条格栅。

格栅尺寸如图2和表1所示，其中a为纵向栅条宽度，c为横向栅条宽度，b为间隔宽度，d为间隔高度，e为格栅厚度。方案1～5 的网格孔隙率β分别为84.02%、88.00%、83.33%、69.89% 和83.96%。为验证试验结果的可移植性，在扬州大学低速直流风洞中进行所设计格栅的对比试验，其试验段的长、宽、高分别为0.4 m、0.4 m、1.0 m。对比格栅如图1（f）所示，网格孔隙率β为67.31%。

表1 格栅尺寸Table 1 Dimensions of the experiment grilles

图2 格栅示意图Fig.2 Sketch of the grille

1.2 试验设计

考虑到风洞试验段轴向长度为3.0 m，为此设计流场测试范围在格栅后1～2 m 位置，共8 个测试截面，格栅距离x分别取值1.0、1.2、1.3、1.4、1.5、1.6、1.8 和2.0 m。为避免格栅受风洞底面近地效应影响，保证测试范围内湍流参数沿高度方向的均匀性，借鉴文献[15]的研究结果，确定垂直方向最低测点高度为0.35 m。测点布置及试验风速测量装置如图3所示。中心测点处于风洞中心线位置，并向左右扩展布置测点。为保证测试截面均匀性满足风洞试验需求，在每个测试截面上布置15 个测点，测点水平间距与垂直间距均为10 cm；垂直方向上共布置5 组测点，且各格栅方案测点相对位置固定。试验中采用DANTEC 公司的热线风速仪（CTA/HWA，55P61）采集瞬时风速数据，热线探头先经标定器（9054H0101）进行速度标定，再通过多通道采集系统（CTA-54N81）、数据采集器（NI_BNC-2110）将采集的电压信号传输至上位机，并依据标定曲线转换为顺风向及横风向速度。测试时确保探头与来流方向平行，两热丝与来流方向成±45°。参考文献[9-10]配置，试验采样频率为5 kHz，共计51200 个数据点。来流风速U分别取15.0、17.5、20.0、22.5 和25.0 m/s，以格栅厚度e为特征长度，对应的雷诺数为3.047×104～5.079×104。

图3 截面上的测点布置及实测装置Fig.3 Sketche of testing points and the arrangement of probes

2 格栅湍流场特性

2.1 湍流强度

以某测试截面某点顺风向湍流强度为例：

其中，Q为采样数据点个数；ui为顺风向脉动风速序列；为合速度的平均速度；σu为顺风向脉动风速的标准差值。横风向湍流强度同样采用上述方法处理。

图4为5 种格栅在不同来流风速下各截面近场区域顺风向湍流强度的测试结果。在测试范围内，来流风速的改变对湍流强度的影响较小。随着格栅距离x增大至1.6 m，格栅后湍流之间的相互耗散使得流场趋于稳定，各方案标准差都显著减小。对各截面测点风速序列利用MATLAB 中adftest函数进行平稳性检验，确定各测点风速均满足平稳性条件。利用顺风向与横风向湍流强度比值（Iu/Iv，Iv为横风向湍流强度）来判断湍流场的各向同性特性。图5为来流风速U=20 m/s 时湍流强度各向同性对比结果。可以看到：竖条格栅Iu/Iv大部分在0.80～1.00，即横风向湍流强度大于顺风向；而在x=1.6 m 处，方型格栅方案1和4 的Iu/Iv=0.96～1.09，这验证了文献[12]结论。就湍流强度而言，当格栅距离x与相邻栅条间隔宽度M比值约为5 时，格栅后流场基本趋于各向同性。3 种竖条格栅各向同性较方型格栅略差，在x=2.0 m处，Iu/Iv=0.90～1.03。这是因为竖条格栅在几何外形上较方型格栅的不对称度更大，气流流过竖条格栅时，横向扩散的幅度也相应更大。

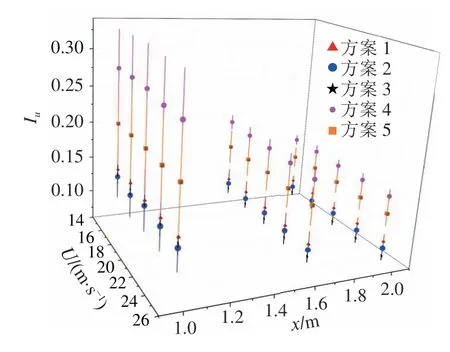
图4 不同来流风速下的湍流强度衰减变化图Fig.4 Decay of turbulence intensity at different wind speeds

图5 各方案湍流强度各向同性对比Fig.5 Isotropy comparison of turbulence intensity with different schemes

图6为来流风速U=20 m/s 时各方案顺风向湍流强度Iu随x的变化曲线，图中误差限为湍流强度的标准差。可以看到：在1～2 m 范围内，5 种方案的湍流强度沿轴向急剧衰减。方案2 与方案3 相比，仅格栅间隔宽度b发生了改变，湍流强度相差较小；方案5 的湍流强度与方案2、3 相比显著提升，说明纵向栅条宽度a对湍流强度影响较大。对比2 种方型格栅，两者栅条宽度（a、c）相差1 倍，但两方案湍流强度均值从x=1.0 m 处的13.55%、27.71%分别减小到x=2.0 m处的9.31%、15.67%。其原因是栅条宽度为3 cm 时，格栅对气流的扰动能力有限，且扰动能力与格栅间隔关联较小；当栅条宽度增大至6 cm 时，气流旋涡脱落幅值增大。对比分析湍流强度较大的方案4 和方案5，两方案的区别在于方案4 中加入了水平放置的栅条，即加入水平放置的栅条可以提高湍流强度、减小标准差。

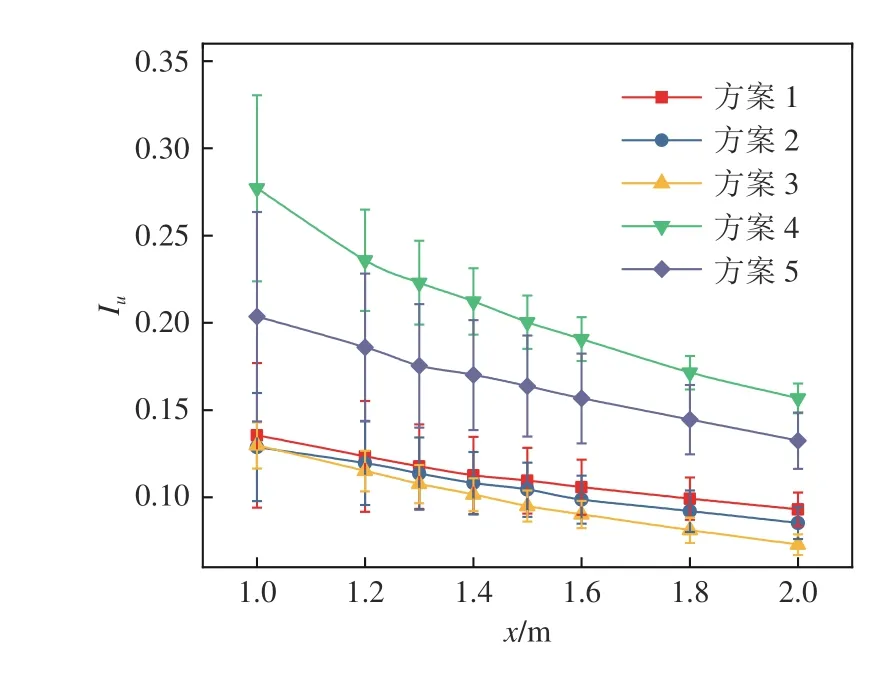
图6 湍流强度随格栅距离的变化图Fig.6 Turbulence intensity at different positions behind grilles

为便于调制局部高湍流场，考虑到湍流强度受格栅的间距、尺寸及网格孔隙率的影响显著，引入x/M1和β进行无量纲化，定义方型格栅M1=竖条格栅M1=a+b。为描述近场区域湍流特性，本文利用二阶多项式进行拟合，对3 cm×3 cm 截面型材组装的格栅流场在x/M1=3～11 时的情况进行预测。忽略近地效应的影响，顺风向湍流强度Iuf（方型格栅）、Ius（竖条格栅）拟合公式为：

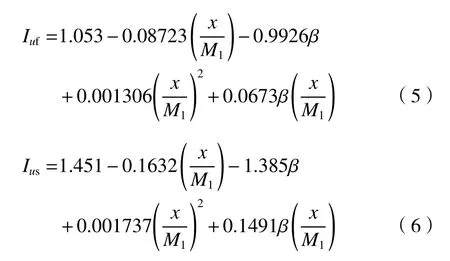
为验证式（5）的可移植性，将拟合公式所得结果与同类试验结果对比，如图7所示。图中绿点为本文对比方案试验结果，红点为文献[8-9]试验结果，蓝色曲面为拟合公式得到的结果。通过拟合优度R2描述试验结果与拟合公式的吻合程度，对比发现：拟合公式和各组实测数据吻合很好，拟合优度R2=0.96，说明本文拟合公式在x/M1=3～11 时预测精度较高。

图7 格栅湍流场湍流强度拟合公式与试验结果对比Fig.7 Comparison of experimental data and fitting formula

2.2 湍流积分尺度

湍流积分尺度表征了湍流场中特征涡旋的平均尺度，实际测量中可基于Taylor 冻结假设，采用单点测量方式和自相关函数求解。假设x点处t时刻顺风向脉动量为u(x,t)，则测点的瞬时速度可视为该点沿顺风向速度的空间变化，脉动风速u(x,t+τ)可以定义为u(x–,τ)。以顺风向为例，平均湍流积分尺度可以写作：

其中，τ、Q–τ为非负整数；Ru(τ)为脉动速度的自相关函数，当τ=0 时，Ru(τ)取最大值σu2；ui+τ为与脉动风速ui间隔为τ的脉动风速值。

图8为来流风速U=20 m/s 时5 种方案顺风向及横风向积分尺度随x变化的试验结果。湍流场中特征旋涡的平均尺度随距离的增大而增大，各方案的顺风向积分尺度Lux在3～12 cm 范围内，顺风向积分尺度约为横风向Lvx的2.5 倍，且随格栅距离x的增大，比值变化不大。这说明格栅后方近场区域中以尺度较小且不对称的特征旋涡为主，且横风向的离散程度较顺风向也有所差异。对比测试结果发现，在格栅后x=1.6 m 处，方案1～3 有着接近的高湍流强度，而顺风向积分尺度依次为0.0648、0.0597 和0.0404 m，方案4 在x=2.0 m 处和方案5 在x=1.6 m 处的湍流强度接近，但积分尺度相差较大，分别为0.0854 和0.1140 m。加装横向栅条后，方案4 顺风向积分尺度小于方案5。显然，对于3 cm×3 cm 截面型材组装的格栅，可通过增大纵向栅条宽度a和间隔宽度b、去除横向栅条的方式提高流场湍流积分尺度。

图8 积分尺度随格栅距离的变化图Fig.8 The integral scale at different positions behind grilles

2.3 湍流功率谱

试验中的测点速度脉动分量可以理解为各种尺寸旋涡的累加，并最终产生由各频率累加而成的脉动能量，可利用瞬时风速序列经离散傅里叶变换得到。除了利用实测值进行谱估计外，还可通过经验谱表征脉动风中不同频率所对应的能量分布情况。以最为常用的Karman 谱为例，其在顺风向的谱密度函数Su(ω)为：

其中，ω为脉动风频率。

传统的周期图法在计算相邻时刻采样序列时是相互独立的，使得功率谱密度谱值噪声较大。因此，在谱密度估计时采用加窗函数的平均周期法（Welch 法），将采样数据Q分为L段，每段数据个数为N，最后一段可向前重叠。以热线采样数据段x(n)为例，则x(n)的总能量等于其傅里叶变换后频域上的面积积分，可得双边谱：

其中，nfft为傅里叶变换点数，X(k)由x(n)经离散傅里叶变换得到。

考虑到傅里叶变换之后存在负频率，因此将这部分频率叠加至正频率上以保证能量守恒。以nfft为偶数时为例，利用幅值谱的平方估计频域能量后，再进行谱估计，即整个数据段的功率谱密度可表示为：

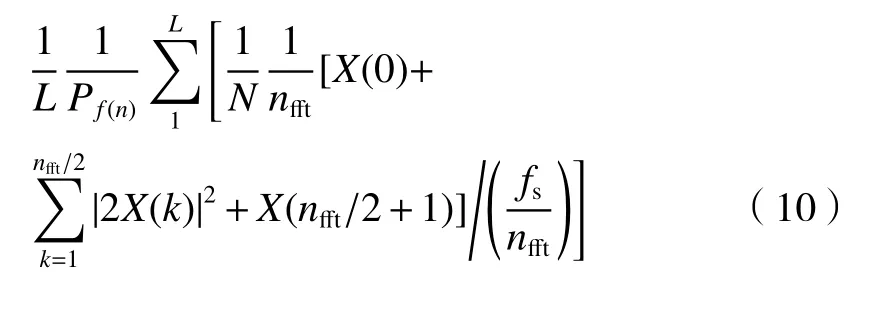
其中，fs为采样频率；Pf(n)为所加窗函数的能量系数，取值为所加的窗函数。

在上述经典的谱估计方法中，需对采样得到的离散序列进行加窗函数操作，这会摒弃窗外的数据；而在现代谱估计中，利用采样数据向外侧递推，以此增加谱估计的精度，但外推的数据不能完全重构数据。因此，采用AR 模型对比估计功率谱密度，具体表达如下所示，这是一个全极点的模型：

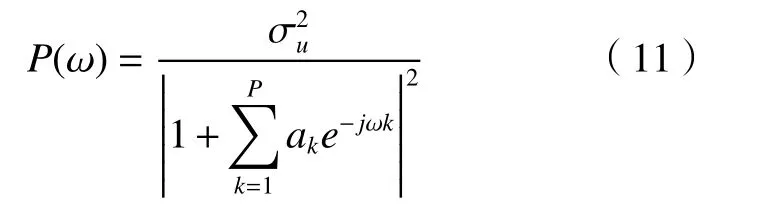
其中，P为模型的阶数，ak(k=1，2，3，···，50)为各阶数的参数。阶数较小时，识别不出峰值相邻的信号；阶数较大时，会产生谱分裂现象，最终选择的模型阶数为50。

图9为x=2.0 处、U=20 m/s 时采用不同谱估计方法得到的方案1 格栅后流场湍流功率谱密度对比，包括加入不同窗函数（Boxcar、Triangle、Hanning、Blackman、Hamming）的经典谱、现代谱（AR 模型）和Karman 经验谱的处理结果。对比发现：3 种谱估计曲线趋势一致，Karman 经验谱在近场区域依然适用。矩形窗函数（Boxcar）的经典谱估计曲线与Karman 经验谱估计曲线吻合得最好。与经典谱估计相比，现代谱估计曲线更为平滑，但两种方法在低频处功率谱密度谱值存在偏差，这是由对随机序列进行分段处理引起的吉布斯（Gibbs）现象所导致。

图9 采用不同方法的湍流功率谱密度比较Fig.9 Comparison of turbulent PSD by using different methods

图10为U=20 m/s 时、方案1 格栅不同格栅距离x的湍流功率谱密度。图11为x=1.6 m 处、方案1 格栅不同来流风速U的湍流功率谱密度。对比发现：功率谱密度变化趋势类似，这是因为相同构造的格栅会使湍流能量在频域的分布具有一定的相似性；但功率谱密度谱值随着格栅距离和频率的增大而向下偏移，在为0.1～0.2 时出现拐点，这说明流场中产生主要能量的涡旋频率在此附近，湍流动能与格栅距离呈负相关、与风速呈正相关。

图10 不同格栅距离的湍流功率谱密度对比Fig.10 Comparison of PSD at different distances

图11 不同来流风速的湍流功率谱密度对比Fig.11 Comparison of PSD with different wind speeds

图12为x=1.6 m 处、U=20 m/s 时，中心测点处不同方案的湍流功率谱密度对比。图中各方案的功率谱密度差别较大，这反映出不同方案脉动风的能量大小存在差异。此时方案1、3、4 中心测点对应的顺风向湍流强度分别为10.5%、9.0%、19.0%，显然，脉动风的能量越大，功率谱密度谱值也越大，且横风向功率谱密度谱值均小于顺风向。与方案4 相比，方案1与方案3 有着更为接近的湍流强度，两者（方案1 与方案3）在低频处差异较大，说明两方案中较大尺度的涡旋结构存在差异；在高频处差异较小，说明在相同型材构造的竖条与方型格栅流场中，较小尺度的涡旋结构具有一定的相似性。结合图10～12 可以看出，通过改变格栅距离x、来流速度U以及栅条结构形式，可以改变湍流场中的能量结构。

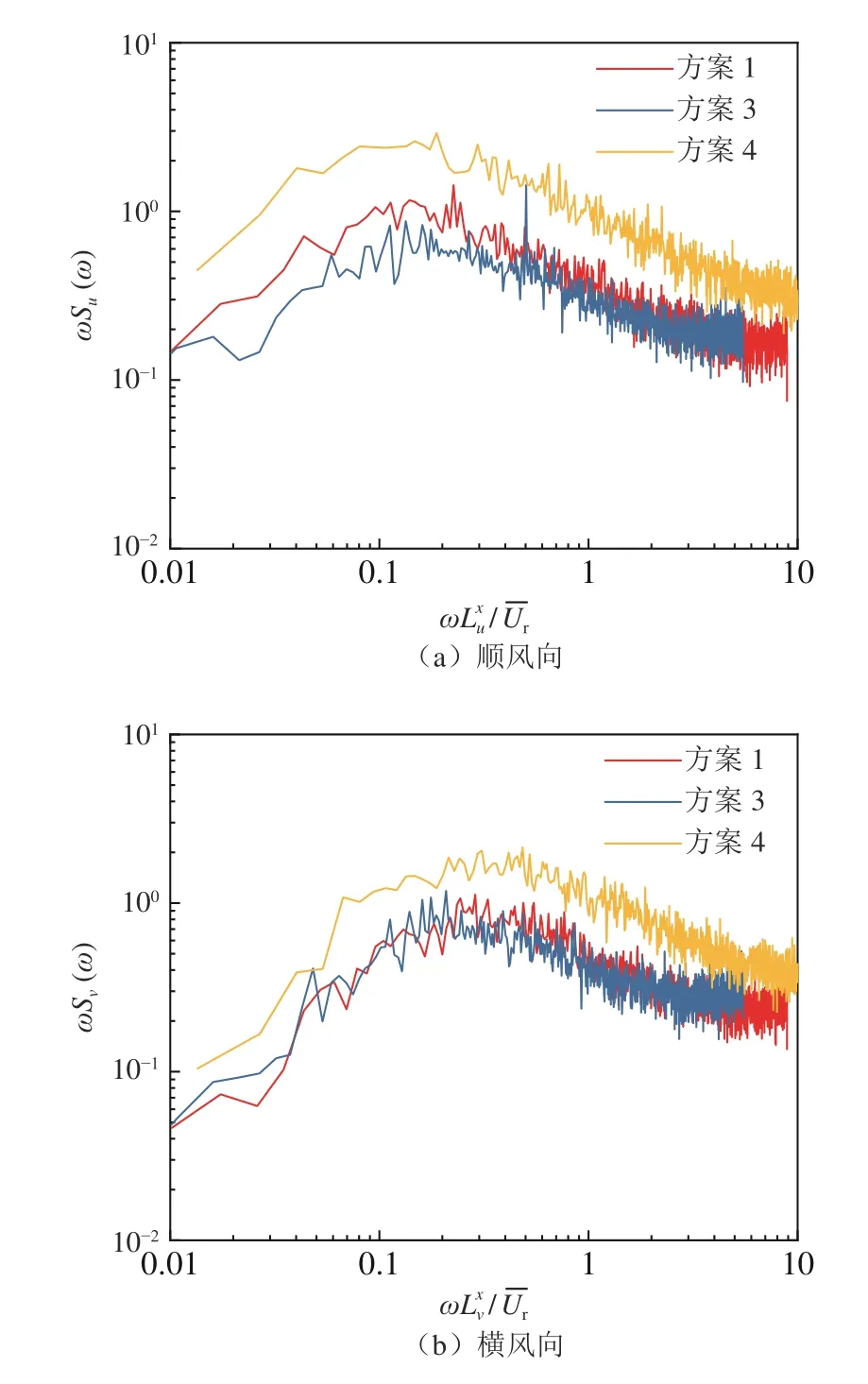
图12 不同方案格栅功率谱密度对比Fig.12 Comparison of PSD with different schemes

3 结 论

在轴向距离较短的风洞试验段中，本文采用3 cm×3 cm 截面铝制型材组装出多种格栅，利用热线风速仪对格栅后近场区域进行测量，分析湍流参数分布特性，得到以下结论：

1）雷诺数在3.047×104～5.079×104范围内，近场区域湍流强度受雷诺数影响较小。在测试范围内湍流强度沿轴向急剧衰减，标准差也显著减小。

2）在近场区域，当测点和方型格栅距离与格栅条尺寸比值约为 5 时，格栅后湍流强度基本趋于各向同性。在测量范围内，顺风向积分尺度约为横风向的2.5 倍，格栅距离增大对积分尺度各向同性性能影响较小。

3）采用Welch 方法估计功率谱密度，并与现代谱及Karman 谱估计进行比较，功率谱密度谱值仅在低频处存在偏差。通过改变格栅距离、来流速度以及栅条结构形式，可以改变格栅湍流场中的能量结构。

本文将拟合的湍流强度经验公式与同类格栅湍流试验结果进行了对比，可为在轴向距离较短的风洞中设计湍流场提供一定参考。