一种面向无人机群区域协同覆盖的深度强化学习方法

姜 波，梁晨阳，梅 杰，马广富

哈尔滨工业大学(深圳)，深圳 518055

0 引 言

在火星探测任务中，火星车由于自身运动限制，无法获得大面积火星地表信息，因此火星车通过携带小型无人机编队来实现对地表的大范围信息采集.无人机编队UAV(unmanned aerial vehicles)具有灵活性、移动空间大等特点，其能够在没有固定基础设施的情况下，提供救援、搜索和基础服务覆盖等服务.例如文献[1]研究使用无人机编队为指定区域提供无线通信服务；文献[2]通过调整无人机编队中每个无人机位置，在陌生环境下为目标点提供实时定位服务；文献[3]使用无人机编队，实现对特定区域中指定目标的搜索，文献[4]通过改进的遗传算法解决有障碍区域的无人机群多目标点路径规划问题.除此之外，无人机编队还可以应用于未知环境探索[5]、区域监视[6]等领域.上述应用都利用了无人机编队的可操作性、灵巧性和鲁棒性.考虑到无人机的速度和姿态的实时调整、地面站到无人机视野的遮挡等复杂环境，使用地面站来控制每架无人机并不可靠.因此，亟需结合具体应用场景，发展一种完全自治、不需要地面站控制的的编队算法.

考虑图1的场景，在地外系统中，当地面车需要获取某一片未知区域的信息时，就可以采用搭载相机的无人机群，这些无人机在目标区域上空散开.每架无人机通过自身机载传感设备对一部分目标区域进行地面信息采集(比如地形、纹理等)，而所有无人机采集到的信息能够覆盖整个目标区域，完成信息采集后编队可以通过离线或在线方式把信息数据发送给地面车辆.在上述场景下，编队需要考虑几个问题：一是由于每架无人机通信范围有限，无人机群之间必须保持通信连接,以保证在距离较远和有障碍物遮挡的情况下，整个无人机群能和地面保持通信连接[7]；二是无人机机载感知设备的覆盖范围有限，可以认为是一个各向同性的圆；三是在地外系统中无人机需要长时间工作，而无人机的能量来源于地面车的太阳能充电，在火星恶劣的沙尘暴环境下，“机遇号”[8]火星探测车上面的太阳能电池板产生电量仅仅能产生晴天的九分之一，因此无人机在工作期间要尽可能减少能量损耗.综上，无人机在上述场景下，受到通信范围约束、感知范围约束和能量有限约束，考虑到每架无人机均是一个独立的智能体，因此需要采用分布式的控制方法.本文的目标是通过设计无人机编队的分布式控制方法，采集尽可能多的目标区域信息.这个问题主要有以下几个难点：一是由于无人机数量有限，需要每架无人机找到最优位置，这样才能采集到尽可能多的信息；二是由于无人机的移动需要消耗能量，需要衡量无人机移动和能量消耗之间的关系；三是无人机不能失去和其他无人机的通信.

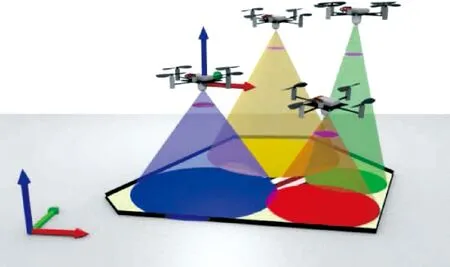
图1 无人机编队对目标区域进行覆盖采集信息Fig.1 UAV formation covers the target area and collects information

为解决上述问题，大量研究利用多智能体系统研究区域覆盖问题[9].在文献[10]中，作者提出一个框架，在这个框架中通过特定的执行参数和系统条件(即剩余能量、计算能力和特定车载传感器提供的能力)，能够对无人机进行编程和管理，以及协调无人机编队行动.为提高智能体搜索目标的效率，在文献[11]中把目标区域分割成若干个大小相同的单元格，并且提出一个统计框架来预测智能体应该在一个单元格中花费的时间量，以增加该单元格中的目标检测置信度.在单元格被智能体覆盖之后，拥有目标的概率会被更新.但是文中需要一个集中式的概率地图来存储每个单元格的概率.文献[12]为解决异构智能体覆盖问题，将这个问题分成了2层，上层是根据每个子编队能力的不同，将目标区域划分给每个子编队，下层是根据子编队中每个智能体的能力不同，将子区域划分给每个智能体.2层的目标函数形式相同.上下2层分别使用不同的分割算法来分割目标区域，目的是为了发挥2种分割算法的优点.文献[13]考虑的是1维的覆盖问题，能够推导出当多智能体系统满足一定条件时，覆盖效果能够达到最好，即目标函数达到全局最优.因此，文章没有对目标函数进行求导，而是在全局最优条件的基础上设计负反馈控制律.此外，控制律的设计还考虑了圆上智能体顺序的保持，不仅能够保证智能体间避免碰撞，还能够简化收敛性分析.文献[14]为找到最优的智能体配置方案，设计了一种“离线+在线”的方法.假设可使用的智能体数量固定，在离线阶段通过贪心算法寻找所有可用智能体初始位置.离线的贪心算法的好处一是能够提供智能体的初始位置，二是能够克服局部最优限制，三是能够提供一个目标函数下界.在线阶段，通过梯度下降算法，一是去除多余的智能体，二是进一步调整智能体位置.通过仿真证明，整个算法总能够使目标函数近乎达到全局最优解.文献[15]为得到离散系统的梯度方向，仅需要对智能体覆盖区域的边界曲线进行积分，这样做好处是减少计算量.此外，文中还设计了智能体移动条件，保证在控制律作用下，智能体的每次移动都能够使目标函数增加.文献[16]以控制质心和智能体实际坐标误差为目标，通过控制律使得误差呈指数衰减.在设计完梯度下降的控制律后，使用模糊逻辑和自适应方法，近似控制律中未知项，并且使用鲁棒覆盖准则减少自适应模糊系统近似误差.文献[17]的控制律设计不同于上述文献，为解决Art Gallery完全覆盖问题，在Max-Sum算法基础上发展出CMGD算法，通过对未知探索区域的近似以及证明Utility Function可导，使得改进后的算法能够使覆盖区域沿着梯度方向变大，适用于离散和连续条件以及适用于智能体全向或扇形探测模型.此外，文章还设计智能体释放策略，通过逐个释放智能体，保证智能体的最大利用.

一些研究成果同样考虑了多智能体系统的约束问题.文献[18]为解决覆盖中的通信连通约束，将约束转换为一不等式约束.此外，在上述不等式约束下，系统容易陷入局部最小值，为解决这个问题，文章在目标函数中加入每个Voronoi图质心到目标区域质心的距离.但是对目标函数如此改造，文中没有给出具体说明或理论证明.文献[19]同样尝试解决连通约束问题，不过文章在维持连通的同时，最大限度提高覆盖范围.文章将这个问题分解成2部分，一是寻找最小生成树，这是维持连通的最小拓扑，二是在最小生成树拓扑下，对CVT的名义控制律输出加上一个Control Barrier Function约束，约束最终控制律输出和名义控制律输出夹角余弦大于零.这种做法不足的地方，一是需要对上述约束分布式化，二是需要智能体在线求解QP优化问题.文献[20]不同于其他算法单纯从图论或者控制器输出来达到连通性约束，而是考虑了路由维护需求，如果不满足路由维护，就把控制律给出的下一时刻坐标点映射到最近的满足路由维护的点上.

深度强化学习近年来同样吸引了很多不同领域的学者研究.文献[21]的作者开创性地引入一个强化学习框架，它使用DQN作为函数近似器，以及经验回放和目标网络2种新技术，以提高学习稳定性.还有其他学者提出许多扩展来解决DQN的限制.文献[22]提出一种DDQN，将深度Q网络和目标网络解耦以避免高估.文献[23]使用重要度采样的方法，提高样本的利用效率.文献[24]提出一种分布式强化学习网络，通过学习折扣回报的分类分布和噪声网络，得到更优的结果.在文献[25]中，作者将上述2种方法以及其他4种方法组合在一个名为“彩虹”的模型中，具有更优异的性能.为解决连续动作空间的问题，文献[26]提出一种基于确定性策略梯度的无模型算法，该算法可以在连续动作空间上运行.其他关于深度强化学习的工作包括文献[27-28].虽然深度强化学习在一些实际的应用场景如游戏、机械臂控制[29]等方面有重要的应用，但它在多智能体系统控制上的适用性和有效性仍未得到有效解决.

多智能体强化学习算法是在单智能体强化学习基础上发展出来的算法，解决群体与环境交互的决策和控制问题.MADDPG[30]算法是对DDPG算法的改进，其能够解决复杂多智能体环境下的问题，MADDPG算法采用了集中式训练分布式执行的方法，在一定程度上缓解了多智能体环境下的非稳态问题.MAPPO[31]算法基于全局状态而不是智能体的局部观测来学习一个策略和中心化的值函数，算法将原本在单智能体环境上表现突出的PPO[32]算法扩展到了多智能体环境上，通过采用一系列的技巧，包括广义价值优势估计、观测值归一化、层归一化和梯度裁剪等，MAPPO算法在多智能体环境下表现出了良好的性能.VDN[33]算法主要解决智能体训练过程中的奖励信用分配问题，通过将团队价值函数分解为单个智能体的价值函数之和，能够有效解决“惰性”智能体的出现.而QMIX[34]算法则是将VDN算法中将各个智能体的价值函数简单相加变为采用非线性组合的方式，并且在混合网络中引入了全局信息，算法解决了智能体数量过多情况下的参数爆炸以及信用分配问题.

本文基于深度强化学习DRL(deep reinforcement learning)技术，提出一种分布式多无人机覆盖控制算法.使用神经网络控制无人机编队的移动，通过定义适当的奖励函数来实现指标的最大化(包括最大覆盖面积、无人机群连通性保持和最小能源消耗).算法采用了参数共享机制，通过采用图神经网络DGN(deep graph network)作为模型隐藏层，模型不会受到因输入的排列不同产生的影响.最后使用本文所提算法和其他2个基线方法进行了比较，结果表明本文所提算法优于其他2种算法.

本文其余部分组织如下.第1节定义系统模型并对问题进行建模.第2节详细介绍本文所提出的算法.第3节介绍仿真实验结果和分析.最后在第4节对本文进行总结.

1 无人机编队覆盖控制问题

本文考虑多约束下无人机编队对2维区域的覆盖问题.无人机编队构成集合N{i=1,2,…,N},集合中每架无人机均能执行覆盖任务，每架无人机的覆盖范围是一个半径为Rsense的各向同性圆，并且无人机的飞行高度固定.我们假设每个时刻无人机能够定位到自身的位置，并且能知道待覆盖区域的形状.

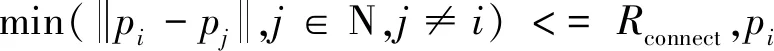
表1 变量名称和含义Tab.1 Variable definitions

(1)

其中φ(q)是表示点重要程度的函数，在区域内每个点重要程度一致的情况下，φ(q)退化为常数1.

综上，本文的目标是通过设计无人机编队的分布式控制律，控制每架无人机到达合适位置，并且最大化覆盖目标区域.无人机编队要同时满足以下要求：一是最大化目标区域的覆盖面积；二是最小化能量损耗；三是保持无人机群的通信连通性.

2 基于强化学习的覆盖控制策略

2.1 基本理论

强化学习可以概括为智能体通过与环境交互来学习策略.在t时刻，智能体获得环境状态值为st，根据自身行为策略π，采取下一步行为at，并且该行为产生的奖励为rt.策略看作是一个从状态到执行动作的概率映射，表示为π(at|st).智能体的目标是通过学习策略，从而在与环境交互时使得未来累计奖励最大化，其数学表示为

(2)

其中T表示最后一个时隙，γ表示折扣因子，取值为0≤γ≤1，rt表示在时隙t时的奖励.

基于值函数的强化学习方法关键在于对智能体动作价值函数的估计.假设在t时刻环境状态值为st，智能体采取行为at，状态-动作价值函数Q(st,at)满足贝尔曼方程

(3)

随着迭代次数j→∞，值函数会收敛到最优值Q*.在Q-learning方法的基础上发展而来的DQN[28]方法，这种方法使用DNN作为函数估计，解决了状态数量无穷的情况，通过最小化损失函数(4)进行训练，损失函数表示为

(4)

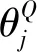
(5)

文献[36]提出的策略梯度方法可以应用于连续系统.令θπ表示行为策略参数，πθπ(at|st)表示在时刻t、状态值st时，采取行为at的概率，ρπ表示在策略π下智能体的状态分布函数.目标函数可以表述为最大化J(θ)=Es～ρπ,a～πθπ[R1].根据策略梯度[36]方法对策略参数θπ进行更新，关于参数θπ的梯度计算方式如下:

(6)

另外可根据“REINFORCE”[35]方法来获取Q(st,at)的值.

在基于“ACTOR-CRITIC”框架的强化学习算法中，ACTOR指的是策略函数的近似值，CRITIC指的是价值函数的近似值.DDPG[26]是这种框架下的一个典型算法，并且ACTOR网络从状态到动作的映射是一个确定的值，这个映射通过μ表示.通过最小化损失函数(4)来对CRITIC网络参数进行训练.ACTOR网络参数更新依照下式

(7)

DDPG也采用了TARGET网络和经验回放池提高训练稳定性.由单智能体DDPG算法发展而来的多智能体强化学习算法MADDP[30]用来解决多个智能体的控制决策问题，每个智能体在训练阶段能够获取到全局的状态信息，在一定程度上解决了多智能体环境的非稳态性.每个智能体需要维护一个CRITIC网络的拷贝Qi.CRITIC网络的参数更新按照损失函数(8)进行

(8)

(9)

2.2 基于强化学习的多智能体覆盖控制算法

本文提出一种基于图神经网络和参数共享机制的多智能体强化学习无人机覆盖控制算法.用来解决在MLP网络中由于输入排列不同而导致的输出不同的问题.

(1)参数共享机制

相比较于MADDPG算法，我们维护一个所有智能体共享的CRITIC网络来指导无人机进行训练，即Q1=Q2=…QN=QG.

MADDPG算法中每个无人机维护一个ACTOR网络，每个无人机还需额外维护一个CRITIC网络.通过CRITIC网络指导无人机对ACTOR网络进行训练，如图2所示.

图2 MADDPG示意图Fig.2 MADDPG schematic

MADDPG算法的网络参数将随着智能体数量的增加而线性增加，CRITIC网络参数的空间复杂度为O(N)，而采用共享机制的CRITIC网络参数复杂度为O(1)，这减少了训练参数的数量，提高了训练的速度，如图3所示.

图3 基于参数共享的Q网络Fig.3 Q network based on parameter sharing

(2)CRITIC网络隐藏层设计

本文使用图神经网络[37]来作为CRITIC网络的隐藏层.对于具有相同动力学模型，相同感知视野的无人机，在不同的时刻，当无人机群的全局状态相同，但输入到全局Q网络的顺序不同时，对于采用全连接层作为隐藏层的CRITIC网络，2种情况下将作为不同的输入处理，从而产生不同的价值函数，如图4所示.

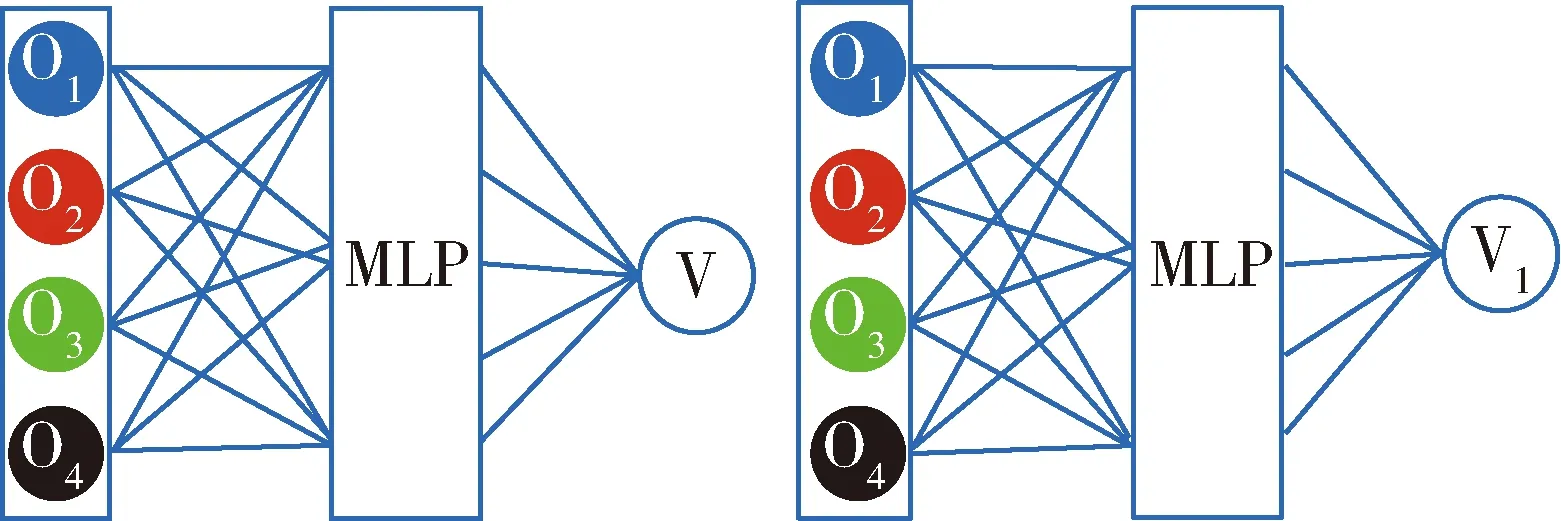
图4 MLP网络结构Fig.4 MLP network structure

图4中4个智能体不同的颜色代表不同的观测值，对于同质的智能体，2种情况下CRITIC获得的全局状态应该是一致的，但是神经网络输出了不同的价值函数.而采用图神经网络作为隐藏层，不会受到因输入的排列而产生的影响.如图5所示，输入到神经网络的无人机观测值排列不相同，然而经过图网络处理后，得到了相同的输出值.

图5 图神经网络结构Fig.5 Graph neural network structure

采用图神经网络的CRITIC网络，其前向传播方式为

(10)

其中fGCN表示图卷积层，fv是全连接层，fmax表示最大池化.zt=[otat]表示所有智能体的观测向量和动作向量的拼接.输入是从右往左传播到输出的，°代表网络的连接.

(3)参数共享和图神经网络强化学习算法设计

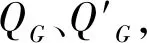
(11)

根据如下的损失函数更新CRITIC网络参数θQ.

(12)

(13)

最后更新ACTOR网络和CRITIC网络对应的TARGET网络参数

(14)

TARGET网络的更新采用软更新的方式，参数τ表示目标网络每次向评估网络移动的距离百分比，采用这种方法，保证了训练的稳定性.完整的训练算法流程如表2所示.

表2 训练算法步骤Tab.2 Training steps

(4)奖励函数设计

关于奖励函数的设计，我们需要考虑以下几点.一是每个无人机自身覆盖到的范围的大小，另外是能量约束以及无人机之间的连通限制.根据以上要求，将奖励函数设计为如下的3个部分

(15)

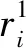
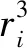
单个无人机的总的奖励函数表示为3部分奖励函数的加权之和.当调整系数a1较大时，表示地面无人车辆需要尽可能多地获取区域的信息，无人机群应该尽可能多的实现对区域的覆盖.取a2较大时，表示无人机群对于能量消耗敏感.取a3较大时，地面无人车希望无人机群能一直保持通信连通.通过在仿真中不断对3个系数进行调整，可以达到一个我们预期的覆盖效果.

3 仿真环境设计与结果分析

3.1 仿真场景与参数设计

本文假设在地外系统中，地面车辆可以携带3架无人机.地面车辆要求无人机群覆盖的区域在实时发生变化.我们模拟地面车辆给无人机群下达的覆盖区域指令从一个半径为R的圆上随机选取4个点得到，如图6所示，取R=5 m，目标区域内每个点的重要程度是一致的取φ(q)=1.

图6 覆盖目标区域(蓝色四边形内)Fig.6 The target area to be covered (inside the blue quadrilateral)

取无人机参数：覆盖半径Rsense=2 m，通信半径Rconnect=5 m，每次迭代无人机移动的单位步长为Δx=0.1 m.

CRITIC网络输入层后面接层图神经网络，图网络的输出层采用平均池化并接一个全连接层.ACTOR网络为4层的网络结构，包含输入层、2层的隐藏层和输出层.输出层输出无人机下一时刻应该移动的方向.隐藏层激活函数使用RELU，输出层激活函数使用TANH.网络权重和偏置采用了正交初始化.在调整a1、a2和a3时，发现3个值都为1可以取得较好的覆盖效果，其他参数如表3所示.

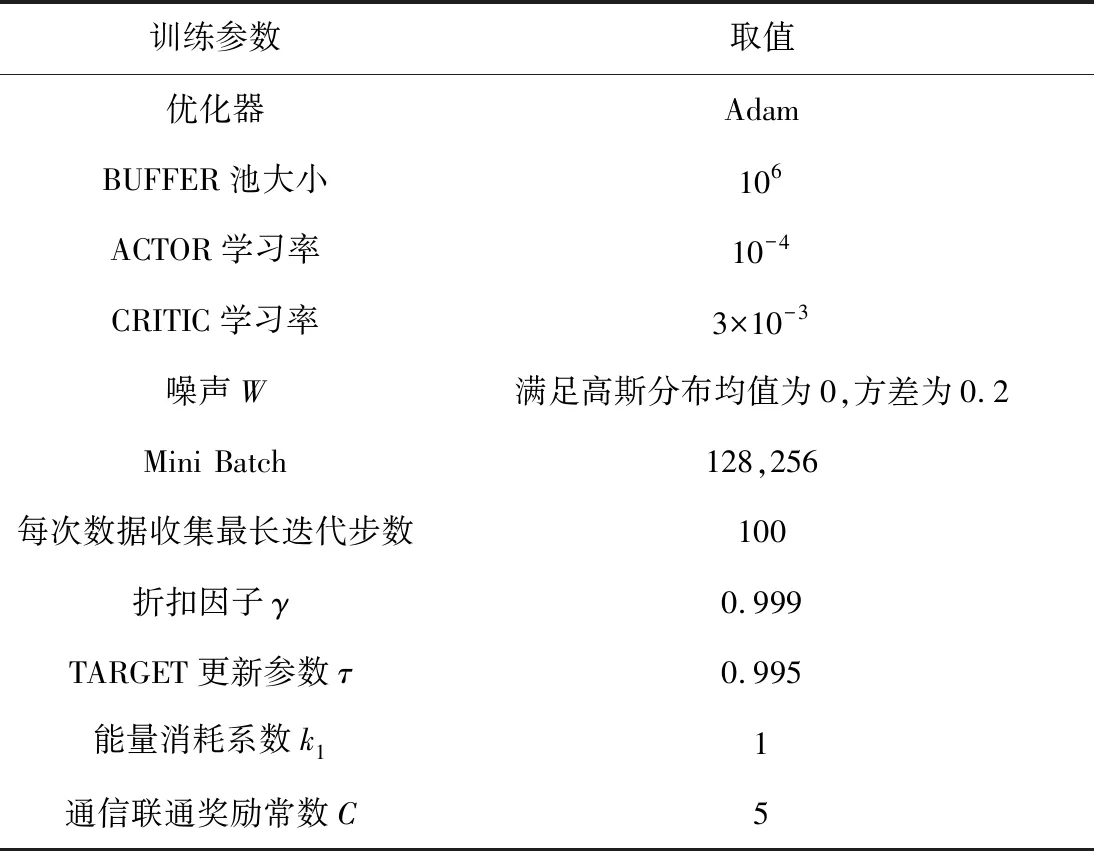
表3 训练参数Tab.3 Training parameters

3.2 仿真结果

我们使用算法构建了模型并对模型进行了2次训练，第1次训练采用的Mini Batch大小为128.第2次训练的Mini Batch大小为256.训练结果如图7～8所示.

图7 训练过程reward变化示意图Fig.7 Schematic diagram of reward changes during training

图8 训练过程loss变化示意图Fig.8 Schematic diagram of loss change during training

2次训练选取不同的Mint Batch大小，从训练过程中的loss变化曲线上看，batch大小为256的训练曲线峰值loss要小于 batch 为128，这符合理论上batch越大，loss的下降方向越符合真实梯度的要求.2次训练loss都先呈现上升趋势，然后稳步下降.经过分析是因为刚开始训练时在动作中加入了随机噪声W，智能体策略倾向于探索.值函数在每一次更新中都去拟合了智能体最新的策略对应的价值函数，值函数的更新快.随着学习步数增加，学习率衰减，随机噪声的去除，智能体策略趋于稳定.reward在训练过程中始终呈现上升趋势，并且最终趋于稳定，说明智能体在训练过程中不断的优化自身策略，并最终获得一个较好的策略.

训练完成后，测试效果如图9所示，其中的圆形代表每个无人机的覆盖范围.图9中3种不同颜色的圆形分别代表3个不同的无人机的覆盖范围，初始阶段随机初始化无人机的位置并使它们保持连通状态，当迭代次数为35的时候到达了覆盖任务中期，图9中的3个无人机始终和自己最近的邻居保持连通，在迭代步数为70的时候，从图9中可以看出无人机已经完成了对目标区域的近似最优覆盖.

图9 覆盖控制算法效果图Fig.9 Overlay control algorithm renderings

为测试算法在无人机群连通性保持方面的表现，我们通过10次对随机目标区域的覆盖来观察无人机群的通信连通保持情况.无人机之间的最大通信距离随着仿真步数变化的情况如图10所示.图中的红色水平虚线是我们设计的通信连通范围限制，当无人机之间的最大通信距离超过红线时，表示无人机网络中存在无人机和集群断开链接.从图中可以看出，在执行覆盖任务的时候，除了初始阶段设定随机初始位置的时候最大通信距离超过了红色虚线，在覆盖过程中所有无人机的最大通信距离始终保持在红色虚线以下，表明无人机群的通信网络始终保持连通.覆盖过程中对目标区域的覆盖比率随着步数更新的曲线如图11所示.

图10 无人机之间最大通信距离变化曲线Fig.10 The curves of max connection distance between UAVs

图11 无人机对目标区域的覆盖比率变化曲线Fig.11 The curves of coverage rate

算法平均在前20步内即完成了对目标区域的近似最优覆盖，覆盖比率呈现稳步上升趋势最终趋于稳定.蓝色曲线有一个上升再下降的过程，分析是因为无人机学习到的覆盖策略在一些形状比较特殊的目标区域下容易陷入局部最优.没有达到百分百的覆盖比率是因为我们假设覆盖区域为圆形，在无人机数量受限情况下无法实现对区域的全面覆盖.

3.3 算法比较

我们使用MADDPG和随机策略2种算法和本文算法进行了比较，任务为覆盖10个不同的目标区域，比较的指标为所有无人机对目标区域覆盖的面积之和取平均值.所有无人机在每次覆盖任务中最多迭代步数为80步.算法运行的环境和初始条件都相同，算法测试得到的曲线如图12所示.

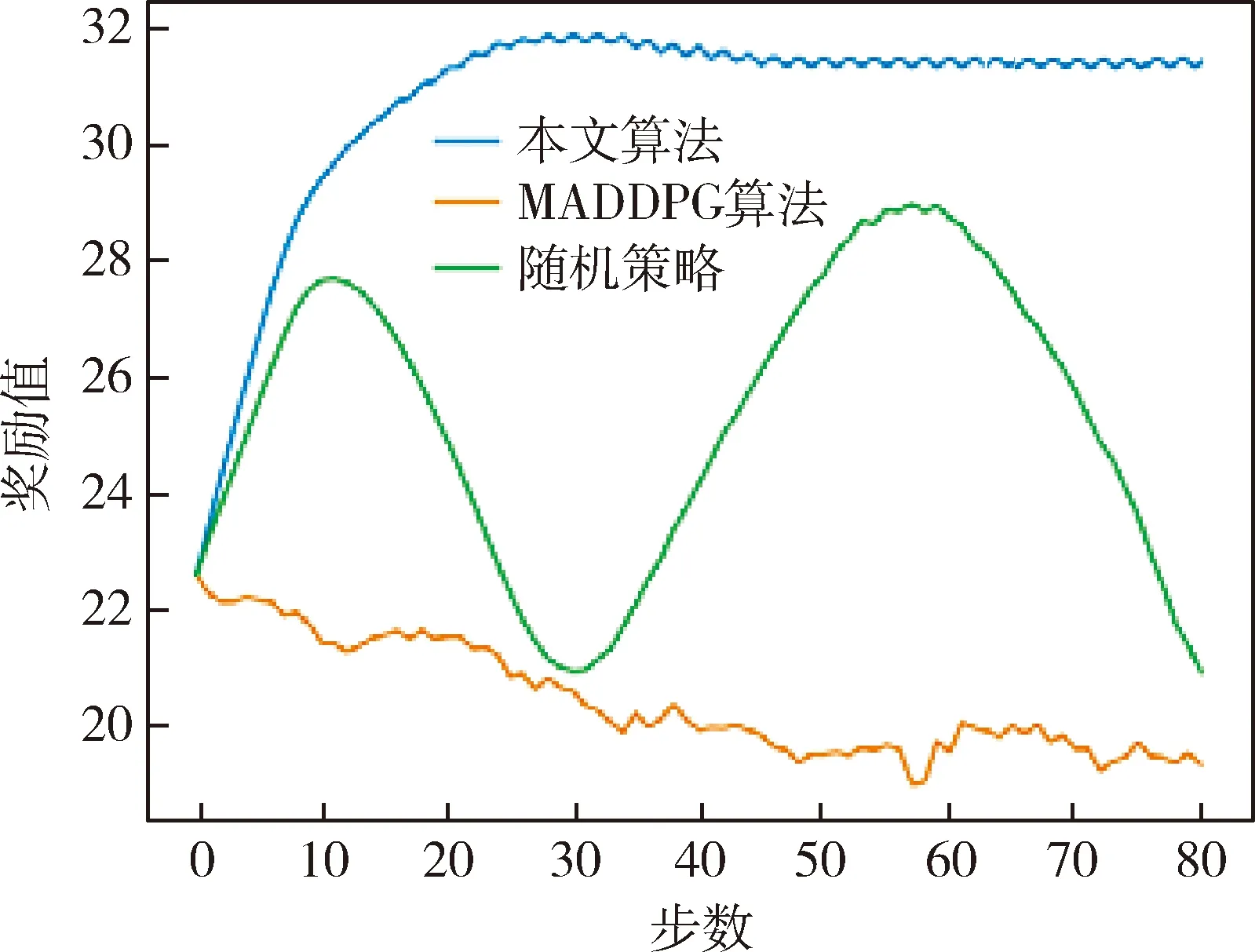
图12 MADDPG、随机策略和本文算法的比较Fig.12 Comparison of MADDPG,random strategy and proposed algorithm

蓝色的曲线代表使用参数共享和图神经网络作为CRITIC网络的策略.绿色曲线代表的是MADDPG算法.橙色曲线代表随机策略，无人机在每个时刻随机的往一个方向移动.从reward曲线上可以看出DGN算法随着步数的增加reward呈现稳步上升趋势，MADDPG算法reward呈现震荡，而RANDAN策略表现最差，reward呈现下降趋势.综上分析，采用参数共享和图神经网络作为CRITIC网络的的多智能体强化学习覆盖控制算法能较好的完成给定的覆盖任务.

4 结 论

地外系统中，尤其是在火星复杂的地表环境下，地面车辆需要获取给定区域的地图信息，无人机群需要在复杂的情况下实现对目标区域的覆盖.本文提出一种基于多智能体强化学习的无人机覆盖控制算法.相比较于传统的无人机覆盖控制算法，本文提出的算法在考虑通信连通性、能量损耗约束方面具有优势.并且所有无人机分布式执行策略.相比较于MADDPG算法，本文提出的强化学习算法采用CRITIC参数共享机制，使用图神经网络解决了状态输入的排列不一致问题.仿真结果表明本文提出的多智能体深度强化学习算法，能让无人机群有效决策实现对目标区域的覆盖.下一步的工作计划考虑无人机的动力学模型，将本文提出的神经网络决策与底层的无人机控制相结合，使得算法更加贴近于真实模型.