海缆有限元温度场的模型验证

何进

（国电象山海上风电有限公司，宁波 315000）

0 引言

海上风电的蓬勃发展对相关技术提出了更高的要求［1-3］，高压海底电缆作为能量传输的载体，更是扮演着一个重要的角色。与常规的陆地电缆相比，海缆的运行环境复杂多变，同时受到船舶锚害等的侵袭［4-5］。为延长海缆使用寿命，避免非自然因素的侵袭，降低维修及敷设费用，目前的风电场建设时会为海缆配备一套监控系统，利用海缆内置的光纤单元结合分布式光纤传感技术，监控海缆的温度、应变、振动状态［6］。这些举措在较大程度上保证了海缆的稳定运行。

在监测的各种状态中，重点监测的是海缆的导体温度。但目前的技术水平难以测量导体的分布式温度，一般通过测量海缆内光纤的温度结合其他计算方法得到的海缆温度场推导出导体温度［7］。但是，目前监控系统的导体温度算法并不完善。为了应对更复杂的环境，确保海缆安全稳定的运行，减少海缆发生事故所带来的安全风险和经济损失，在将有限元法应用到监测系统之前，应该对有限元法计算的温度场进行验证。

1 验证流程

验证分析以海缆稳态温度场为主。对于瞬态温度场而言，侧重于分析海缆温度场的变化趋势。这是因为海缆结构相对复杂，且敷设环境复杂多变，难以确定其准确的变化过程。首先，需要从大量的原始数据中筛选出符合条件的数据并加以处理；然后确定所选数据对应海缆处的建模参数；最后分别对稳态和瞬态温度场进行建模验证。验证流程如图1所示。

图1 验证流程

2 工程数据处理

2.1 温度数据处理

提取海缆某一位置各个时间点的温度数据，得到该点处的温度变化曲线，然后对该温度变化曲线进行滤波处理，下图是海缆6600 m处的光纤温度变化趋势图。

图2中横轴表示监测数据文件的生成时间点，纵轴为温度。可以看出，在2019年8月9日到11日三天时间内，光纤的温度一开始处于上升趋势，最后保持稳定。对提取的数据进行滤波处理，得到如下结果：

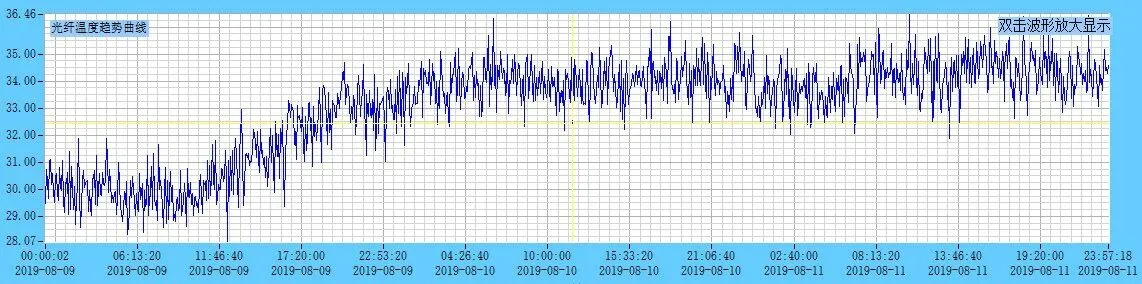
图2 海缆光纤6600 m处温度变化

监测系统记录的导体温度数据是根据光纤温度数据推导出来的，因此导体温度的处理和光纤温度的处理类似。对于6600 m处的导体温度趋势如图4所示。

图4 6600 m处导体温度趋势

2.2 电流数据处理

在海缆有限元温度场的计算中，需要计算海缆内各部分的损耗。这些损耗是海缆通电后产生的，一般根据电流大小来计算。特别的，在瞬态温度场的求解中，需要考虑电流随时间的变化，因此需要找到电流与时间之间的关系：

式中，ct为t时刻海缆的通电电流。因此对于电流数据的处理，一般先进行滤波处理，再根据电流的变化趋势，选择合适的拟合方法对其进行拟合。图5为电流的原始数据及对应滤波后的图像。

图5 海缆电流变化

从图5中可以看出，当电流相对稳定时，会在一定范围内波动，这种情况下，难以计算应当施加在海缆内的载荷，因此需要对其进行拟合。

在进行稳态问题的分析时，施加的载荷是一直不变的，可电流是在一直变化的，因此将变化的电流等效为稳定电流进行计算。在图6中展示了海缆通电电流变化曲线，另外通过图3可以看出光纤温度在时间点1000附近达到最大值，因此对时间点150～1100内的电流进行等效处理。由焦耳定律有：

图3 6600 m处光纤温度趋势

图6 海缆电流拟合

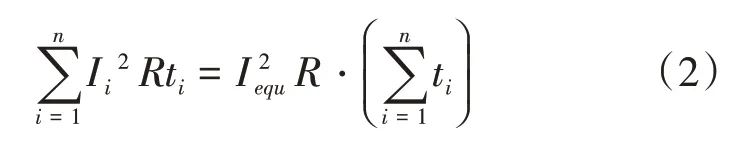
式（2）中，Ii为某段时间内的电流值；ti为Ii持续时间；Iequ为等效电流。求出等效电流约为360 A。

3 稳态温度场的验证

使用有限元法计算海缆温度场，首先需要对海缆及海缆所处环境进行物理建模，然后给定各部分材料的物性参数，并对整个模型进行网格划分。同时将电流转化为生热率载荷施加到对应部位并确定整个模型的边界条件，最后对整个模型进行求解得到海缆温度场。

从图7中发现在等效电流360 A通电下6600 m处光纤的稳态温度约为34.63℃。在提取有限元温度场中的光纤温度时，考虑到光纤单元作为一个整体，其内各部分对光纤的温度具有一定影响，因此对光纤单元各处进行采样取平均值。其各点处的温度值如表1所示。

图7 海缆温度场云图

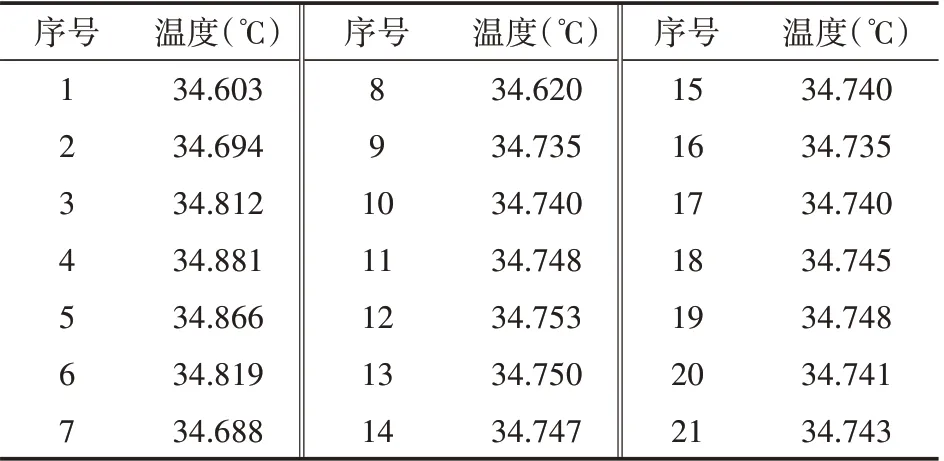
表1 光纤单元各处采样点温度列表

计算得到采样平均值为：34.74℃。故有限元计算结果与实测结果间的绝对误差为：0.11℃。它们之间的相对误差为：0.32%。

从图4中发现在等效电流360 A通电下6600 m处导体的稳态温度约为42.33℃，同样在整个导体区域进行采样。其各点处的温度值如表2所示。

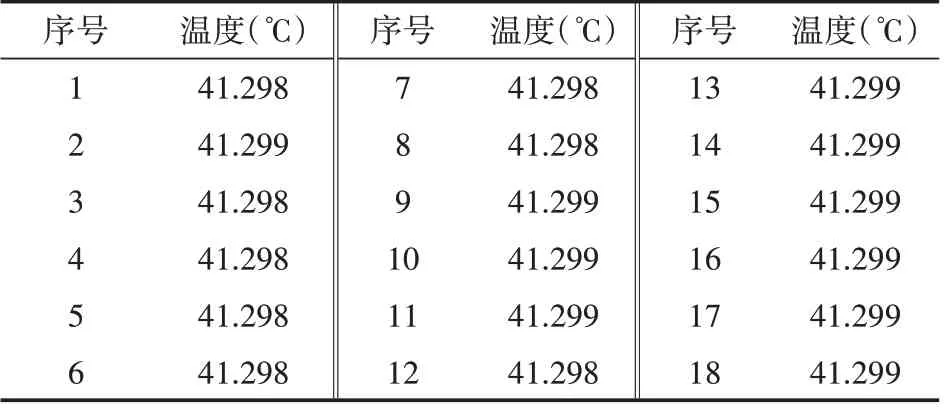
表2 导体区域各处采样点温度列表

计算得到采样平均值为：41.30℃。故有限元计算结果与监测系统推算结果间的绝对误差为1.03℃。它们之间的相对误差为2.43%。

4 瞬态温度场的验证

瞬态建模过程与稳态建模过程类似。对于瞬态温度场的求解，需要根据时间与电流的关系转换为时间与载荷的关系。通过求解得出温度随时间的变化趋势。

从有限元模型中提取光纤不同时刻的温度数据。其变化趋势如图8所示。

图8 瞬态温度场中光纤温度趋势

从图8中可以看出使用瞬态分析计算的光纤温度变化趋势与实际测量的光纤温度变化趋势基本一致，各点处的绝对误差与相对误差如图9所示。

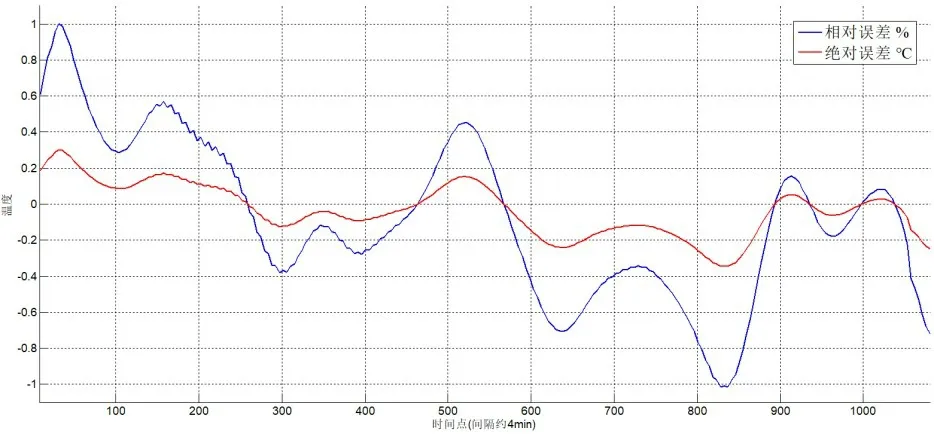
图9 光纤温度误差

从图9中可以看出有限元计算出的光纤温度与实测光纤温度绝对误差最大为0.35℃。两者之间的最大相对误差为1.02%。瞬态分析的结果进一步表明有限元温度场的准确性。

通过同样的方式，获得导体温度随时间的变化趋势如图10所示。

图10 瞬态温度场中导体温度趋势

从图10中可以看出使用瞬态分析计算的导体温度的走势与监测系统推算的导体温度走势基本一致，各点处的绝对误差与相对误差如图11所示。

图11 导体温度误差

图11中有限元计算出的导体温度与监测系统推算的导体温度之间绝对误差最大为2.08℃。两者之间的最大相对误差为5.61%。综合上述分析可知，通过有限元计算得到的海缆温度场较为准确。同时发现监测系统推算的导体温度虽然相对准确，但仍具改进空间。因此在后续监测系统导体温度算法更新时，可采用有限元法替换现有算法。

5 结语

本文从海缆的监测数据出发，确定海缆有限元温度场的建模参数。通过有限元法计算出海缆的稳态和瞬态温度场，计算结果与实测数据的对比分析表明了有限元温度场的准确性。