建设工程项目激励模型中的激励失效问题优化研究
吉格迪,杨 康
(内蒙古工业大学 经济与管理学院,内蒙古 呼和浩特 010051)
国民经济中,建筑业占据了很大的比重,这些年来,建筑项目的规模不断扩大,涉及的工艺难度越来越大,需要的技术水平越来越高,但是整体的管理方法却不能满足行业发展的需要,造成工程施工的各个环节问题频发。因此,工程过程管理的重难点就是如何用最有效的方式激励承包单位主动完成工程目标。一直以来,有很多研究者对此问题进行了分析,得到很多显著的成果。最初,经济学家Berle及Means提出一种全新的观点,称为委托代理。它针对存在利益冲突以及信息不对称的环境,解决一方如何采用最优契约来激励另一方的问题。自此,开启了委托代理理论的先河,学者们纷纷以此作为切入点,研究一系列激励问题。王绪民等[1]利用委托代理模型既实现了成本管理的目标,又使工人的收入达到最优。郭汉丁等[2]采用双重委托代理激励模型,同时加入博弈理论,找出使质量最优的激励参数。房勤英等[3]将模型扩展到不止有一个委托方的情况,在此情况下分析各方在项目进行中的行为、目标及各自的相关关系。张家旺[4]则实现委托代理理论与信息经济的结合,分析承包商同时进行多个工作时的激励情况。陈勇强等[5]分析多任务的委托代理模型,目标函数采用Cobb-Douglas生产函数的形式。Gallagher等[6]认为通过这种激励方法能够使工程的运营情况发生显著改善。Chang等[7]研究发现,委托代理理论中,最优风险分担原则与激励系数的大小存在很大的相关性。
相关研究越来越深入,研究者们考虑到每个人的专业水平、信誉情况均有所差别,这些可以作为声誉评价的指标,一方能够通过另一方的工作表现来衡量,并将声誉评价的结果列入绩效考核中,影响收入的高低。所以,如果将委托代理模型重复应用在工程进行的各个阶段,一方的声誉水平将关系到当期甚至将来的收益,也因此可以更好地约束承包商,主动实现工程目标。基于此,研究者们逐渐将声誉和委托代理模型相结合。这一理论的先河是在1980年,Fama[8]认为声誉评价能够充当一种非完全替代的手段,不论是否存在显性的激励方式,承包单位都将保护他们在行业中的声誉,以获得更高的收入。Holmstrom[9]将Fama的理论上升到模型的角度。考虑到声誉情况,刘惠萍等[10]提出动态的激励模型,模型同时考虑了声誉和显性激励两种方式。曹启龙等[11]以PPP项目作为研究的切入点,将声誉动态激励与之相结合。孔峰等[12]考虑到国有企业一些经理人的职业特点,站在公司长远收入最大化的角度构建模型,同时考虑双重声誉和股票期权激励。时茜茜等[13]通过双重声誉与显性激励两者融合的多阶段激励模型,实现重大工程工厂化预制商的动态激励。在委托代理和博弈理论的基础上,马力等[14]提出一种新的合约形式,合约考虑两种激励,一种是显性激励,一种是基于声誉的隐性激励,并提出优化合约激励的有效方式。郑梅华[15]在声誉的基础上,提出承包商的“公平偏好”这一理念,建立短期静态、长期动态两种模型。Chi等[16]考虑团队成员的工作能力及合作倾向两种声誉情况下的激励。段永瑞等[17]在激励模型中考虑成员的共享、协同两种情况,分析声誉在整个激励过程中的效果。整理发现,在考虑声誉之后,整个激励模型与实际情况更切合,激励效果也更显著,但往往考虑工程各指标间协同性的激励模型缺乏对声誉的考量,一部分计入了声誉的模型又是在各指标相互无关联的假设下进行的。因此,如果将以上提到的模型运用在工程项目的全过程,则容易发生激励失效的情况,具体有以下表现:如果模型不考虑承包商的声誉,则只能实现静态激励,不能根据工程进行中的一些具体情况完成有效的动态调整。事实上,大型长期工程中的承包商都会看重声誉效应,从而主动遵守合同的规定,如果忽视声誉实施激励,则容易出现激励过剩;假如考虑声誉因素,但模型为单要素激励模型,那么合作方会基于激励的条件,过于重视某一目标的完成情况,各要素间的关联性常常被忽略,产生激励失衡,使多要素协同发展的目标无法完成。
基于以上研究,本文提出的模型综合工期、质量两个项目要素间的相关性,是一种协同激励模型,同时引入承包商的显性、隐性声誉实现动态激励,进一步与加入了声誉的单要素激励模型、未引入声誉的协同激励模型对比。本文给出使双重声誉多要素协同激励模型能够生效的有效区间的判断方法,并采用算例及数据模拟的方式进行验证。
1 考虑双重声誉的多要素协同激励模型
1.1 模型假设
假设1契约双方需要完全理性,即一切选择的出发点都是各自获得最优的利润,同时双方不可能得到同样的信息资源,即信息不对称,作为被激励的一方获得的私人信息较多一些,这一点实施激励者无法作出直接的判断,但是能够准确得到的信息是承包单位在项目的进行过程中创造的产出。
假设2在此把工程分为两个阶段,努力水平aij>0,其中,i=1表示工期因素;i=2表示质量因素;j=1,2表示处于工程的第j个阶段。R(a1j,a2j)=A1a1j+A2a2j+ϕa1ja2j+ζ代表了工程项目的价值增值函数,函数里A1、A2为产出系数,用来衡量投入努力对产出的直接影响;ϕ是关联系数,表示两要素之间的相互影响;ζ是随机变量,代表外部不确定性对产出的影响,满足Hyers-Ulam稳定性, ζ∼N(0,σ2),ϕ=0。
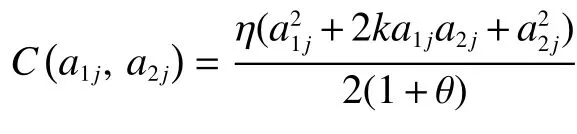
假设4设定双方的风险偏好类型,业主方为中性,承包单位对风险采取规避的态度;在此认为承包单位的负效用函数具备不变绝对风险规避的特征,在状态和时间两个方向上具有可加性,进而提出风险成本的表达形式为ρVar(S), 其中, ρ>0代表承包单位的绝对风险规避度;S代表承包单位在过程中得到的收入。
假定5承包单位通过投入努力创造的项目产出为x(x1j,x2j),x1j=γ1j+ha1j+ε1j,指项目在工期上的缩短或延迟,其中,j代表所在的项目阶段;x2j=γ2j+qa2j+ε2j,为项目在工程质量上的完成情况,可以理解为工程质量抽查的合格率、优良率等;h>0,q>0, 用来衡量承包单(位的投)入对项目产出函数x1j、x2j的 边际影响; γij∼N0,ij表示承包单位的显性声(誉指标),比如个人能力、业绩、信誉情况等;εij∼N0,ij衡量外在不可控因素对产出的影响,这种影响因子独立于努力水平,γij、εij相互独立。
假设6根据委托代理模型,承包单位获得的收入采取线性函数为S j=ϖj+β1jx1j+β2jx2j,ϖj是固定收入的部分,j代表项目所在阶段,考虑为一个常量; βij>0衡量边际激励的大小,分工期、质量两种情况。
假设7在初步合作时期,对承包单位的声誉情况并不了解,业主在进行激励时,只能从现有信息中判断一个大致值。当项目完成一个阶段后,业主方会以已完工程情况为依据,对其声誉值进一步判断。在此用到理性预期公式。


条件方差公式为
Var(xi2)=E[Var(xi2|xi1)]+Var×[E(xi2|xi1)]。
故
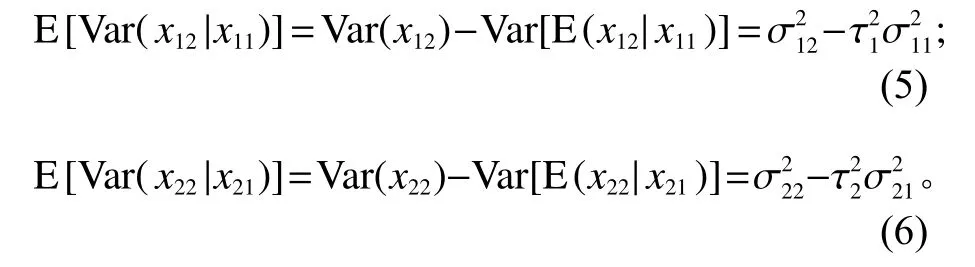
1.2 模型建立与求解
声誉激励机制发挥作用的前提是委托代理模型的循环应用,因此把签订了长期契约的委托代理双方划为两个阶段。在本文提出的模型中,双方在初始阶段的表现将关系到下一阶段的收入情况,所以在重复长期的声誉激励的约束下,双方将出于长期收益的考虑作出决策;进入第2阶段后,处于项目的最后一个阶段,此时长期声誉激励的影响失效,双方仅考虑当前收入情况。基于此,模型如下。
1.2.1 第2阶段最优激励模型
基于上述理论,对风险持规避态度承包单位的期望收益为

进一步,风险中性业主方在最终阶段的期望收益为

基于双方获得的信息不对称,最佳决策方案将同时受βi2、ai2的影响,模型约束条件考虑为参与约束、激励相容约束,则第2阶段的激励模型为
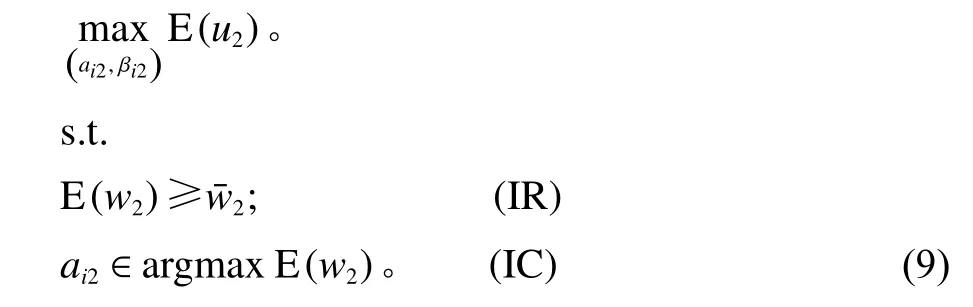



求解找到βi2的最优值,此时的工期、质量两要素实现协同发展。
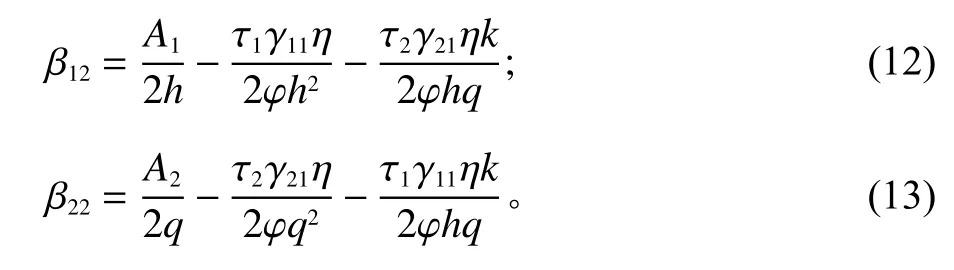
1.2.2 第1阶段最优激励模型
由于承包单位在这一时期投入的努力会影响这一时期收入的同时,也会对下一个阶段的收入产生影响。所以,在当前阶段,双方作出的决策是基于前后两个时期的总收入情况。
此时,风险规避型承包单位前后两阶段总期望收益为

同理可知,业主在这一时期总期望收益公式为

得到这一时期的最优激励模型为



与第2阶段相同的处理方式,将最优努力水平代入第1阶段模型的目标函数,得到业主方两阶段收益的期望效用函数的偏导函数为

解偏导函数得这一阶段的最佳激励系数,同时实现工期、质量两要素的协同发展。
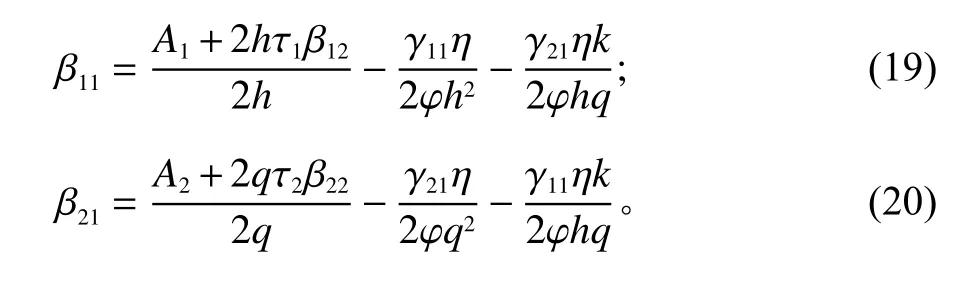
2 两种传统激励模型介绍
在之前提到的两种传统激励方式:加入声誉的单因素激励模型、未引入声誉的各要素协同激励模型作为切入点,与本文讨论的双重声誉的多要素协同激励模型对照。考虑到传统模型的探索已经非常普遍,因此直接列出模型及最优解。
2.1 加入声誉的单要素激励模型
2.1.1 工期激励模型
以只关注工期的单目标激励模型为例,加入声誉因素的作用后,在第2阶段的激励情况为

其中,
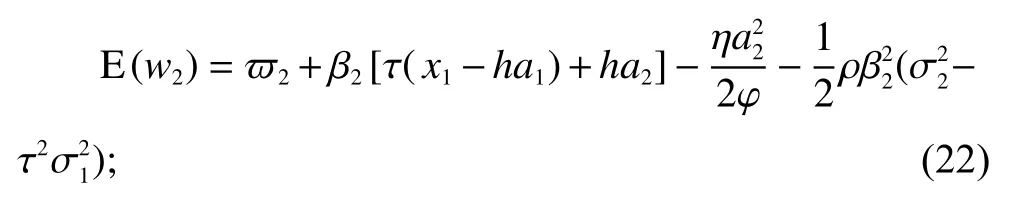

进一步给出在第1阶段的激励条件为
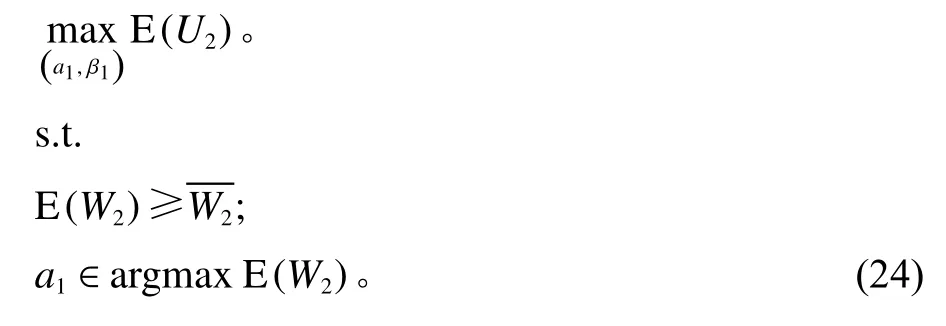
其中,

对上述问题求解,得到
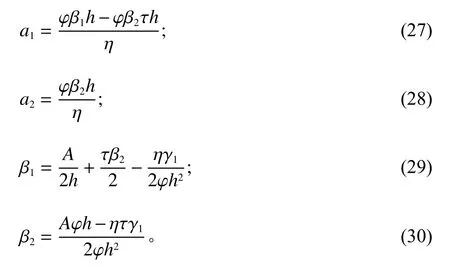
2.1.2 质量激励模型
假如单因素激励模型以工程质量作为关注点,此时的激励情况与2.1.1节中提到的工期激励非常相似,仅在一些参数的取值上有所不同,故给出模型的最优激励公式为
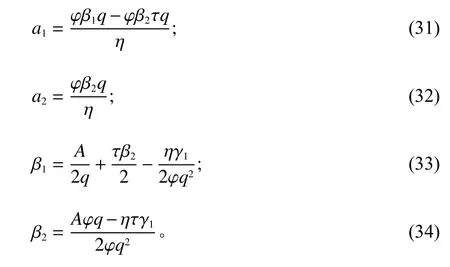
其中,q>0,表示一方为了保障工程质量付出的努力水平情况对应项目产出函数的影响。
2.2 未引入声誉的协同激励模型
此时模型中承包单位的期望收益函数为

另一方,业主得到的收益为
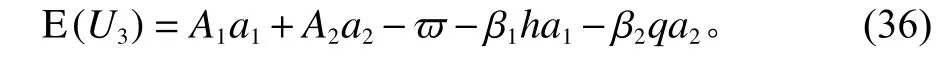
进一步,将承包方在整个契约关系中的激励相容约束和参与约束作为模型的条件,目标函数考虑为业主方期望收益的最优,得到

同理,应用委托代理模型的求解方法,得到最优的努力水平和激励系数为
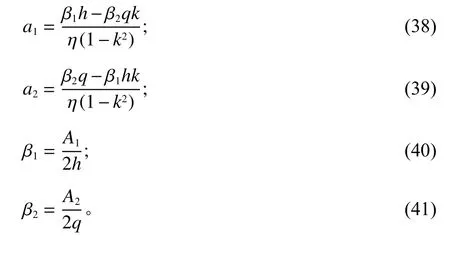
3 模型对比分析
3.1 模型对比
命题1从最优激励系数的大小考虑,本文提出的模型在工期激励上优于传统的单要素激励模型。
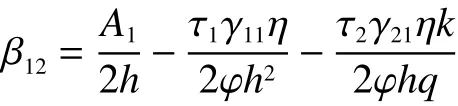
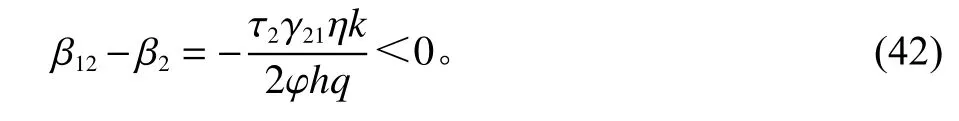
总结来说,在工期要素上,本文提出的模型能够以较小的激励系数实现预期成果,帮助业主方降低成本。
命题2同样从最优激励系数的大小考虑,本文提出的模型在质量激励上优于传统的单要素激励模型。

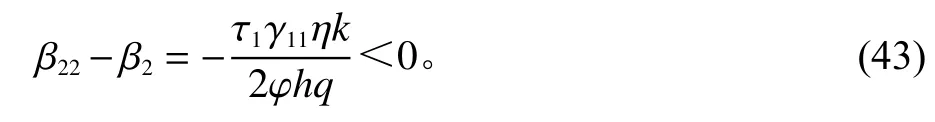
同理,在质量要素上,本文提出的模型能够以较小的激励系数实现预期成果,帮助业主方降低成本。
由命题(1)、(2)可知,本文提出的模型总体要优于传统的单要素激励模型。原因在于,本文提出的模型同时考虑了工期、质量两个因素,避免激励失衡现象的出现,同时又能够以较小的激励实现项目的成本节约。
命题3与未加入声誉激励的协同激励模型相比较,本文提出的模型在最终阶段的激励系数较小,这也说明采用本文提出的双重声誉协同激励模型,能够帮助激励者以较低的成本实现项目预期目标。
证明

因此, β12<β1,β22<β2。
命题4从工期这一项目要素上的最佳努力水平来看,本文提出的模型在满足特定条件时,能够实现最终的努力水平超过未加入声誉激励的协同激励模型。
证明

令式(46)大于零,求解得,当φβ12h−β1h≥k(φβ22q−β2q)得到满足时,模型中承包单位在工期要素上的最佳努力水平可以明显提高。
命题5参考命题4,从质量这一项目要素上的最佳努力水平来看,仍然能够取得相同的结论。
证明

令式(47)大于零,求解得到,本文提出模型中质量因素上最佳努力水平优于未加入声誉激励的协同激励模型的一般条件为 φβ22q−β2q≥k(φβ12h−β1h)。
命题3~5将本文提出的双重声誉协同激励模型与未加入声誉激励的协同激励模型对比发现,本文提出的模型在考虑了声誉要素对承包单位心理上的影响后,不论是最优激励系数还是最佳努力水平上都有所提升,从而未加入声誉激励的协同激励模型激励过剩的现象得到进一步改善。
3.2 双重声誉多要素协同激励模型有效区间的确定
有效区间的作用机理在于,项目开始之前,业主方对被激励者的声誉有一个判断值。假设判断值正好位于模型的有效区间之内,则选择本文建立的双重声誉协同激励模型最终激励结果会优于没有考虑声誉的模型,此时选择本文提出的模型是业主方的最佳选择;反之,这一判断值不在有效区间时,那么本文建立的模型可能并非最优。因此,在本节研究双重声誉协同激励模型有效的一般条件,从而给出有效区间的确定方法。
研究分别考虑业主方、承包单位、社会总价值3种情况下的有效区间。在满足以下条件时,本文的双重声誉协同激励模型可以实现最优:假设从业主方的角度考虑,3个模型下得到的业主单位的期望收益函数中,双重声誉协同激励模型为最优,此时模型有效。所以得到模型有效区间的确定方法,是要找到3个模型中各自期望函数收益曲线的交点,得出γ11、 γ21的两个端点值,即模型的有效区间,具体方法如下。
本文提出的双重声誉协同激励模型中业主的收益期望函数为
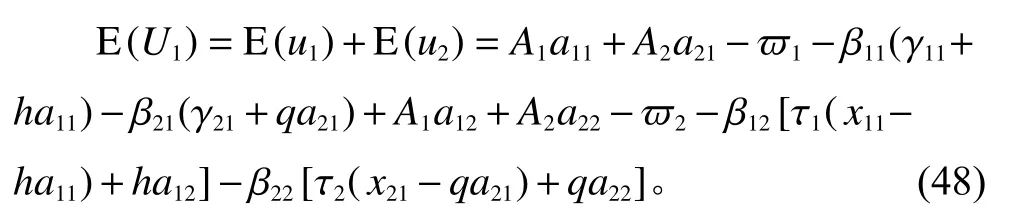
工期单因素激励模型下业主方的收益期望函数为

未考虑声誉的协同激励模型中业主的收益期望函数为

将式(48)、(49)、(50)联合求解即为使业主方收益最优的声誉值的有效区间。结果通过Matlab软件模拟即可得到γ11、 γ21的两个端点值。考虑到计算结果过于冗长,在此不再表述。
4 算例分析和数据模拟
4.1 算例分析
4.1.1 承包商低声誉水平的情况
以一公路工程的施工过程为例,承包单位的收入分为固定收益和绩效工资两个部分,参考模型的前提条件:设产出系数A1=,4 5A,2=分4别0代表工期、质量两个方向;固定收益 ϖ1,= 50 ;ϖ2=50工期、质量上努力水平的边际成本替代率k,=0.3因此对工期上投入努力水平会增加质量上的边际成本;成本函数中 η =,2 φ =;1.5在初始阶段,承包单位的声誉取较低值 γ11=,3 γ21,=对5应修正指标,τ1=0 .1。 其τ2他=0参.1数 为 ,h,= 1q,=1ρ=0.6,σ11,=,0.,005 σ12=0.01 σ21=0.005 σ22=0.01σγ11=,0.0016σγ21=0.0016;其余3个传统模型中相关参数的取值参照上述指标。对全部模型求解得到表1。

表1 承包单位为低声誉水平时模型结果对比Table1 Comparison results in the case of low reputation contractors
通过分析表1得到以下结论。1) 与传统的工期、质量单因素激励模型相比较,在最优激励系数上,双重声誉协同激励模型较小;从收益情况上分析,双重声誉协同激励模型中业主及承包单位的收益较传统激励模型要高。以上情况表明双重声誉协同激励模型可以通过激励系数的减少,为业主方实现降低项目成本的目标。2) 与未加入声誉的协同激励模型相比较,双重声誉协同激励模型最终激励系数β12、 β22较 小,努力水平a12、a22较大,双方最终收益相对较高。3) 比较低声誉情况下双重声誉协同激励模型过程中的激励系数,发现 β12>β11,β22>β21,表明在承包单位水平较低时,业主方要增加激励的强度才能达到工程目标。
4.1.2 承包商高声誉水平的情况
假设承包单位的声誉水平较高,对应的有关参数的具体值需适当调整,例如相比低声誉水平的情况,声誉值、声誉修正指标需适当提高,因此γ11=4,γ21=6, τ1=0.4。 τ2=0.4。考虑到声誉激励的作用,对某一项目目标投入努力后,相对于另一目标成本的影响减弱,相应成本降低,故k=0.2, η=1。除此之外声誉要素方差适当增加,取σγ11=0.0032,σγ21=0.0032。模型中其余数值参考4.1.1节。通过模拟计算,得到4种模型在高声誉水平下的最终结果如表2所示。

表2 承包单位为高声誉水平时模型结果对比Table2 Comparison results in the case of high reputation contractors
从表2结果发现,本文提出的模型最终激励系数较小,而收益水平却有所增加。对比发现β12<β11,β22<β21,所以基于承包单位较强的工作水平和信誉情况,此时不需太大强度的激励,而模型就能够以较低的激励系数实现协同发展,表明模型可以根据承包单位的不同情况实现动态调整。
4.2 数据模拟
选择低声誉水平的情况,选用软件Matlab进行数据模拟计算,找出低声誉情况下本文提出的考虑双重声誉的多要素协同激励模型的有效条件;获得考虑双重声誉的多要素协同激励模型、传统的单因素激励模型、未加入声誉的协同激励模型相比之下,业主方、承包单位以及社会总价值三者与声誉的相关关系,即图1~8,进一步分析,找到3个视角下模型的适用条件。
1) 图1选择的模型为传统的工期单因素激励模型与考虑双重声誉的多要素协同激励模型。将两种模型中双方的最终收入情况进行对比,发现随着声誉值的变化,考虑双重声誉的多要素协同激励模型的收益都在传统的工期单因素激励模型之上。

图1 双重声誉协同激励与工期单因素激励模型下双方收益与γ 的关系Figure1 The Relationship between owners 'and contractors' revenues and γ under the dual reputation co-incentive model and the duration incentive model

图2 双重声誉协同激励与未引入声誉的协同激励模型下双方收益与γ11 的关系Figure2 The relationship between owners 'and contractors' revenues and γ 11 under the dual reputation co-incentive model and the co-incentive model without considering reputation

图3 双重声誉协同激励与未引入声誉的协同激励模型下双方收益与γ21 的关系Figure3 The relationship between owners 'and contractors' revenues and γ 21 under the dual reputation co-incentive model and the co-incentive model without considering reputation

图4 双重声誉协同激励与未引入声誉的协同激励模型下双方收益与γ 11、γ21 的关系Figure4 The relationship between owners 'and contractors' revenues and γ 11、γ21 under the dual reputation co-incentive model and the co-incentive model without considering reputation

图5 双重声誉协同激励与工期单因素激励模型下社会总价值与γ 的关系Figure5 The relationship between total social value and γ under the dual reputation co-incentive model and the duration incentive model

图6 双重声誉协同激励与未引入声誉的协同激励模型下社会总价值与γ11的关系Figure6 The relationship between total social value andγ11 under the dual reputation co-incentive model and the co-incentive model without considering reputation

图7 双重声誉协同激励与未引入声誉的协同激励模型下社会总价值与γ21 的关系Figure7 The relationship between total social value andγ21 under the dual reputation co-incentive model and the co-incentive model without considering reputation

图8 双重声誉协同激励与未引入声誉的协同激励模型下社会总价值与γ 11、γ21 的关系Figure8 The relationship between total social value andγ11、γ21 under the dual reputation co-incentive model and the co-incentive model without considering reputation
2) 图2~4为考虑双重声誉的多要素协同激励模型与未加入声誉的协同激励模型的对比结果。从图形中可以直观地找到有效区间,γ11属 于区间[−35.5,51.5],γ21属 于区间[ −29.5,53]时,能够满足期望收益大于等于零。所以,承包单位的目标首先是使自身的声誉值落在上述区间,进一步,为了使自己的保留效用得到满足,承包单位将不断改善声誉值,促使最终收入超过自身的可接受值。
3) 从业主方收益考虑,在某一范围内,激励水平与承包单位声誉成正比,而此时自身收益将与对方的声誉值成反比,这一情况会在超过某一特殊点后开始反转。
4) 从承包单位的收益考虑,γ11属 于区间[ −22,37],γ21属 于区间 [−17,39]时考虑双重声誉的多要素协同激励模型优于未加入声誉的协同激励模型;从业主方收益考虑,γ11属 于区间[ −∞,8]以 及[ 64,+∞],γ21属于区间 [ −∞,10]以 及 [ 52,+∞]的情况下,考虑双重声誉的多要素协同激励模型优于未加入声誉的协同激励模型。
5) 图5~8是社会总价值视角下,不同模型的对比情况。从图5来看,考虑双重声誉的多要素协同激励模型的模拟结果显示,社会总价值永远优于传统的单因素激励模型。图6~8则表明,承包单位的声誉值不断增加,社会总价值表现为先增后减,同理找到考虑双重声誉的多要素协同激励模型的有效区间为γ11属 于区间 [ −170,28],γ21属 于区间 [ −92,36]。
5 结论
本文在传统研究的基础上,加入了两方面的因素:1) 为了反映出工程目标中工期、质量间相互替代的关系,在成本函数中加入边际成本替代率k这一概念;2) 结合承包单位的声誉对本期收益和长期项目成本的影响,建立双重声誉作用下的协同激励模型。为了证明模型可以很好地消除激励失效现象,特将本模型与传统的单因素激励模型、未加入声誉的协同模型作比较验证,证明了模型的有效性,并提炼出本文提出的模型能够有效发挥作用的相关条件。最后,应用Matlab软件,采用数据模拟的形式,分析高、低两种声誉条件的承包单位的情况,证明本文提出模型的可行性和有效性。模型验证结果表明,在有效区间内,经过分阶段对模型的重复应用,能够动态调整承包单位的声誉值,不断贴近实际情况,从而选择不同的激励水平,同时提高承包单位在工作中的积极性,充分有效地分配项目资源,达成多要素协同发展,使得业主、承包单位、社会总价值三方收益不断改进。
当然,文章的研究也有几点欠缺之处。考虑到理论与实际工程情况的局限性,难以找到完全一致的工程实例,因此采用算例分析以及数据模拟的形式,故相关结论还需在工程实施过程中进行考证。另外,声誉机制的有效应用,还依赖于工程建筑体系信用机制的改进,因此,还需进一步规范工程建筑市场。

