Positive Solutions for a Class of Fourth-Order Problem Under Nonlocal Boundary Value Conditions
ZHU Ying(朱颖), MA Yenan(马烨楠), ZHANG Guowei(张国伟)
(Department of Mathematics, Northeastern University, Shenyang 110819, China)
Abstract: In this article, we study a class of fourth-order problem with the second derivative in nonlinearity under nonlocal boundary value conditions.Some inequality conditions involving spectral radius on nonlinearity are presented that guarantee the existence of positive solutions to the problem by the theory of fixed point index on a special cone.Two examples are provided to support the main results under mixed boundary conditions including multi-point with sign-changing coefficients and integral with sign-changing kernel.
Key words: Positive solution; Fixed point index; Cone
1.Introduction
In [1-2], the authors studied the existence of positive solutions respectively for the following two fourth-order boundary value problems (BVPs)

and
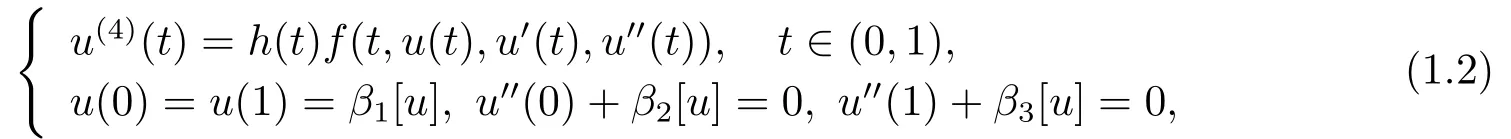
whereβi[u] =dBi(t) is Stieltjes integral withBiof bounded variation (i= 1,2,3).Notice thatu′′(0) =u′′(1) in (1.1) but may not hold in (1.2), and the different methods are used in [1-2] under different conditions.
In this article, we discuss whether the method similar to one in [1] is still valid when the boundary conditions for (1.1) are replaced by the more general ones for (1.2), that is, the existence of positive solutions to
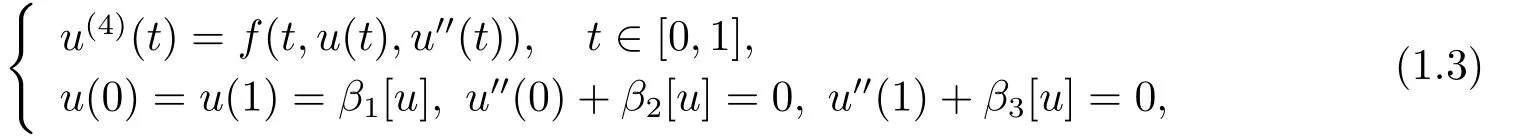
and the answer is positive.Also some faults in [1-2] are pointed out.The readers may refer to [3-17] and references therein to get more information and techniques about relevant issues.
2.Preliminaries
LetX=C2[0,1]consist of all twice continuously differentiable functions on[0,1],and it is a Banach space with the norm‖u‖C2=max{‖u‖C,‖u′‖C,‖u′′‖C},where‖u‖C=max{|u(t)|:t ∈[0,1]}foru ∈C[0,1].We make the following assumptions:
(C1)f:[0,1]×R+×R- →R+is continuous, here R+=[0,∞) and R-=(-∞,0];(C2) For eachi ∈{1,2,3},Biis of bounded variation and
where
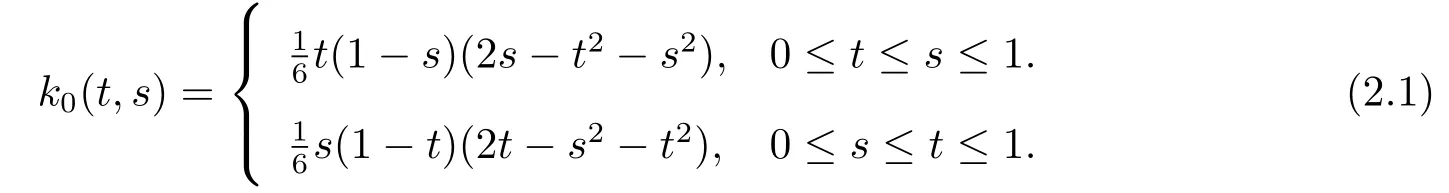
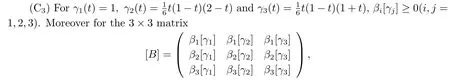
its spectral radius isr([B])<1.
Remark 2.1In [2],γ2(t) was miswritten as1-t)(5-t) so that subsequent calculations were affected.See Remark 3.2 in Section 3.
Under (C1)-(C3) we define operatorSinC2[0,1] as follows:

where

in whichK(s) = (K1(s),K2(s),K3(s))Tandγ(t) = (γ1(t),γ2(t),γ3(t))Tare the transposed vectors,〈(I-[B])-1K(s),γ(t)〉is the inner product in R3, andκi(s) is theith component of(I -[B])-1K(s).By [18] we have that BVP (1.3) has a solution if and only if there exists a fixed point ofSinC2[0,1].
Lemma 2.1[2]If (C2) and (C3) hold, thenκi(s)≥0(i=1,2,3),

and fort,s ∈[0,1],
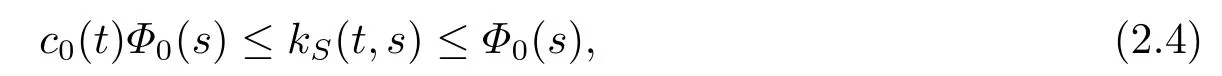
where

and
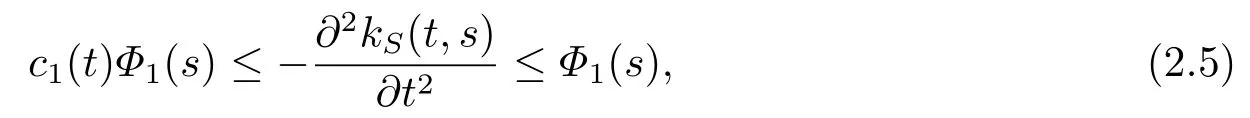
whereΦ1(s)=κ2(s)+κ3(s)+s(1-s), c1(t)=min{t,1-t}.
Remark 2.2In [2],c0(t),Φ1(s) andc1(t) were respectively mistakenly written as(t)+γ3(t), 2κ2(s)+κ3(s)+s(1-s) and min{t,(1-t)/2}.
Define two subsetsPandKinC2[0,1] as follows:
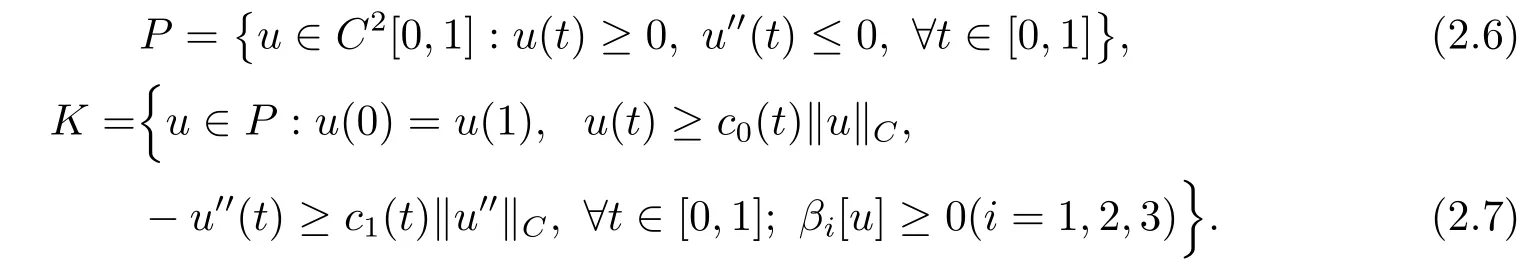
Also define linear operators

whereai,bi(i= 1,2) are nonnegative constants.Similar to Lemma 2.6 in [2] we have the following lemma.
Lemma 2.2If (C1)-(C3) hold, thenS:P →KandLi:C2[0,1]→C2[0,1] are completely continuous operator withLi(P)⊂K(i=1,2).
LetXbe a Banach space, a nonempty subsetPinXis called a cone if it satisfies the conditions: it is a closed convex set;λx ∈Pfor anyλ ≥0 andx ∈P;±x ∈Pimpliesx=0(the zero element inX).We need the following properties about cone and fixed point index(see [19-20]).

3.Main Results
Theorem 3.1If the hypotheses (C1)-(C3) are satisfied, suppose that
(F1) There exist constantsa2, b2≥0 andr >0 such that

for (t,x1,x2)∈[0,1]×[0,r]×[-r,0], in addition, the spectral radiusr(L2)<1;
(F2) There exist positive constantsa1, b1, C0satisfying

such that
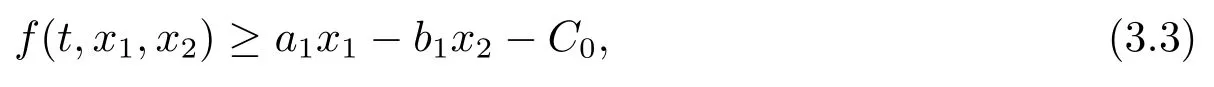
for (t,x1,x2)∈[0,1]×R+×R-.
Then BVP (1.3) has a positive solution.
Proof(i) We first show thatforu ∈K ∩∂Ωrandμ ∈[0,1], whereΩr={u:‖u‖C2<r}.In fact, if contrarily there existu1∈K ∩∂Ωrandμ0∈[0,1] such thatu1=μ0Su1, then we have from

and (3.1) that fort ∈[0,1],

Thus (I -L2)u1≼0.Because the spectral radiusr(L2)<1,I -L2has a bounded inverse operator (I - L2)-1:P →Pandu1≼(I - L2)-10 = 0, a contradiction is deduced tou1∈K ∩∂Ωr.
Consequently,i(S,K ∩Ωr,K)=1 by Lemma 2.3.
(ii) Let

It is clear from (3.2) thatM >0.Foru ∈Kwe define the homotopyH(λ,u) =Su+λv,where
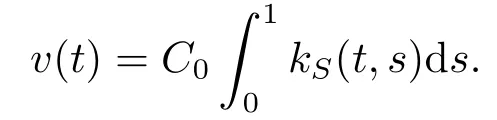
Thusv ∈Kby Lemma 2.1 andH:[0,1]×K →Kis completely continuous.
LetR >max{r,M}and now we prove that

Otherwise, there existu2∈K ∩∂ΩRandλ0∈[0,1] such that


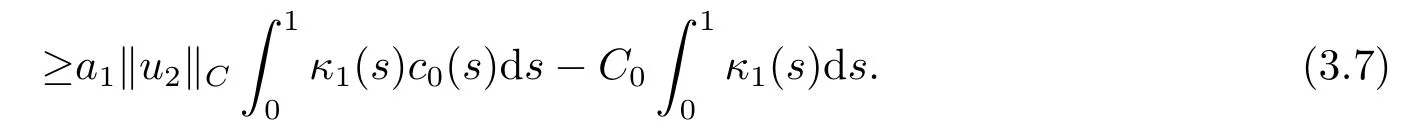

Therefore, from (2.2) and (3.3) we have
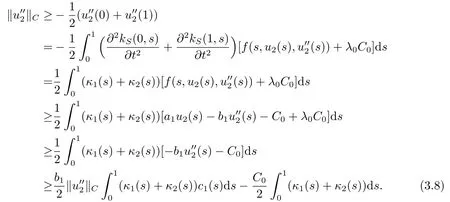
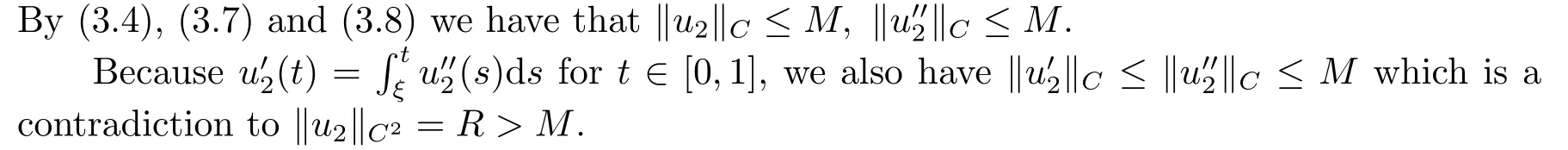
From (3.5) it follows that

by the homotopy invariance property of fixed point index.
(iii) Define a linear operatorLinC[0,1] as below.
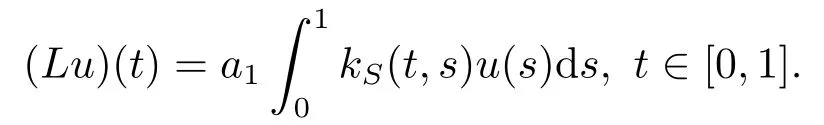
We can easily prove thatLis completely continuous satisfyingL(C+[0,1])⊂K ⊂C+[0,1],whereC+[0,1]={u ∈C[0,1]:u(t)≥0, ∀t ∈[0,1]}is a cone inC[0,1].Forc0(t) in Lemma 2.1, we have from (2.4) that

From Lemma 2.1 and (3.2) it follows that

Accordingly there existλ1>λ0andφ0∈C+[0,1]{0}such thatφ0=λ-11L3φ0∈Kby Lemma 2.6.
(iv) Now we show thatu-H(1,u)0foru ∈K ∩∂ΩRandν ≥0.
If there existu0∈K ∩∂ΩRandν0≥0 such thatu0-H(1,u0)=ν0φ0, thenν0>0 by(3.5) and
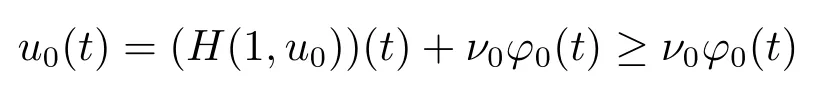
fort ∈[0,1].Denote
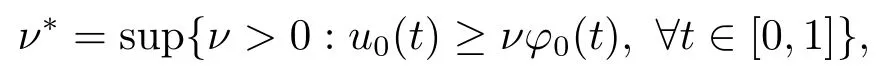
thenν0≤ν* <+∞andu0(t)≥ν*φ0(t) fort ∈[0,1].From (3.3) we have that fort ∈[0,1],

Sinceλ1>1, we haveλ1ν*+ν0>ν*, a contradiction to the definition ofν*.
Consequently, by Lemma 2.4

(vi) From (3.9) and (3.10) it follows thati(S,K ∩ΩR,K)=0 and

HenceShas a fixed point, namely, BVP (1.3) has a positive solution.
Remark 3.1In [1], the analogues of (3.7) and (3.8) are derived by dividing three different situations to discuss.Actually, those are unnecessary since bothu2(0) =u2(1) and0) =(1) are therein satisfied, meanwhile, both(t) and(t) are monotone.They mean that only one case occurs.
Theorem 3.2Suppose that the hypotheses (C1)-(C3) are satisfied, and
(F3) There exist constantsa1, b1, C0≥0 such that

for (t,x1,x2)∈[0,1]×R+×R-, in addition, the spectral radiusr(L1)<1;
(F4) There exist constantsa2, b2≥0 andr >0 such that

for (t,x1,x2)∈[0,1]×[0,r]×[-r,0], in addition, the spectral radiusr(L2)≥1.Then BVP (1.3) has a positive solution.
ProofThe proof is similar to those of Theorem 2 in[1]since they therein relied only on the Krein-Rutman theorem (Lemma 2.5) and the boundary conditionu(0) =u(1) preserved in this paper.

D1= [0,1]×[(4/27)τb,b]×[-2b,2b]×[-2b,0], D2= [0,1]×[0,16b]×[-2b,2b]×[-b,-τb],andf(t,x1,x2,x3)for (t,x1,x2,x3)∈D3=[0,1]×[0,16a]×[-2a,2a]×[-2a,0], then BVP (1.2) has at least one positive solution.
4.Examples
We consider fourth-order problems under mixed boundary conditions involving integral with sign-changing transcendental function kernel and multi-point with sign-changing coeffi-cients
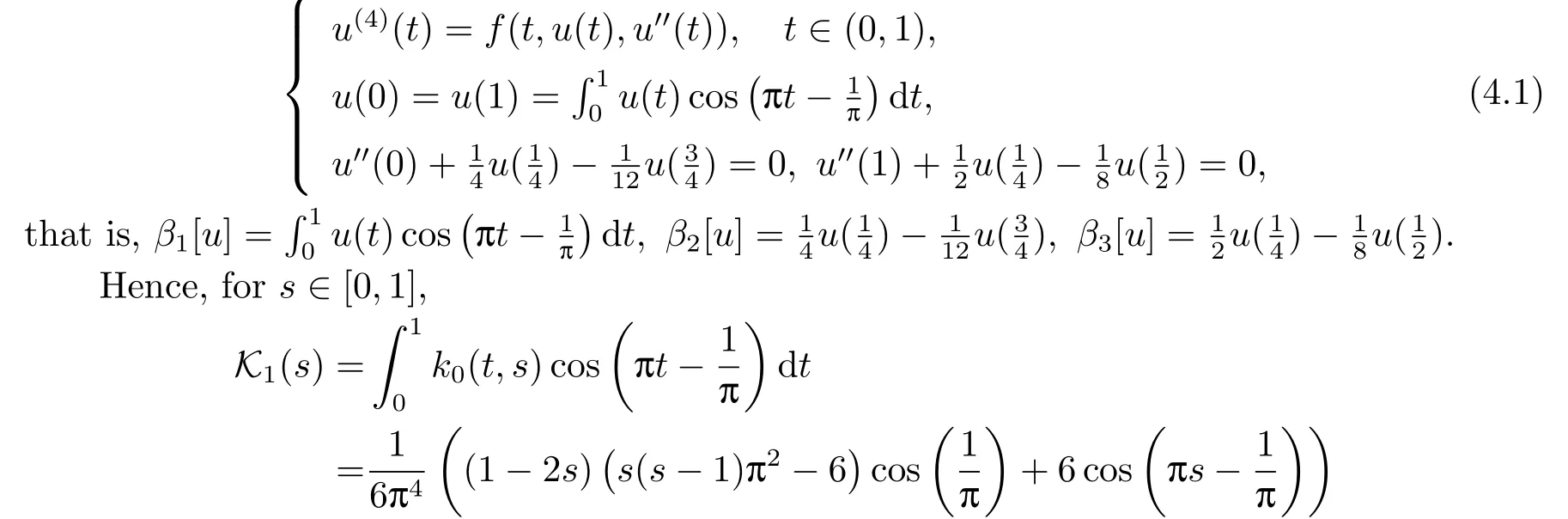
with 0≤K1(s)≤0.0034,
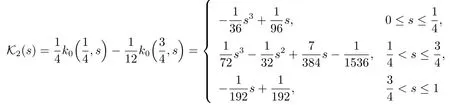
with 0≤K2(s)≤0.0026,
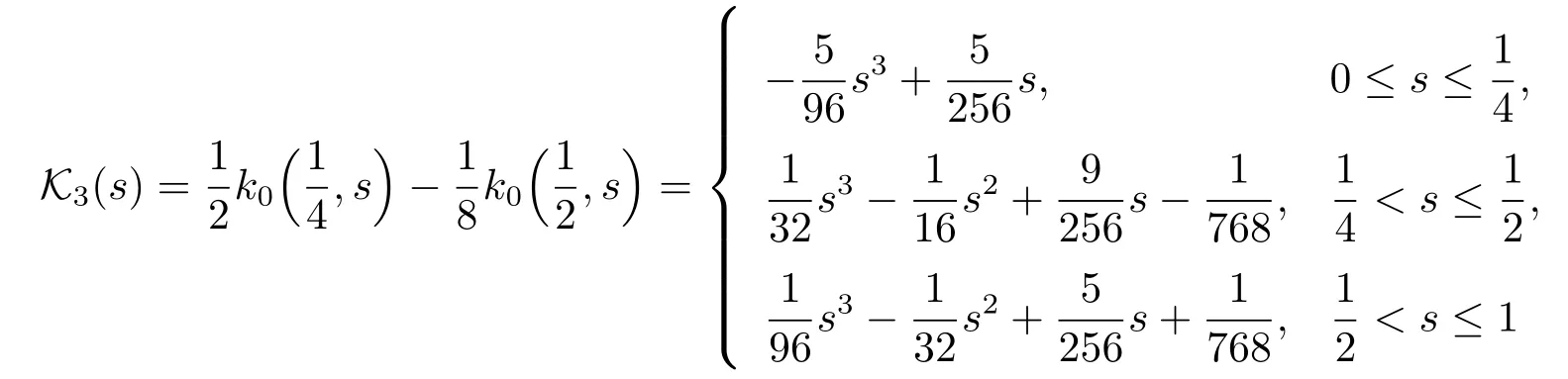
with 0≤K3(s)≤0.0048.The 3×3 matrix

and its spectral radius isr([B]) ≈0.2227<1.This means that (C2) and (C3) are satisfied.Moreover,
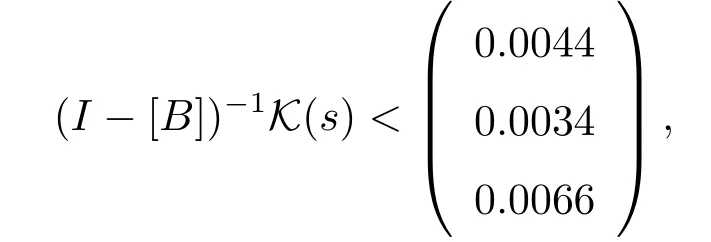
thus

So foru ∈C2[0,1] andt ∈[0,1],

hereLi(i= 1,2) are defined in (2.8).Since both the left side and the right side have the same polynomial forms with positive coefficients in (4.2) and its second derivative int, the inequality relations are decided by its coefficients.Thus foru ∈C2[0,1] andt ∈[0,1],

By Lemma 2.1 we have

and then there existsη ∈(0,1) such that (Liu)′(η)=0.Therefore fort ∈[0,1],

and‖(Liu)′‖C ≤‖(Liu)′′‖C.Therefore the radiusr(Li)≤‖Li‖≤0.2551(ai+bi)<1 if

Example 4.1If

then BVP (4.1) has a positive solution.
Takea1=10000, b1=2000.It is clear that
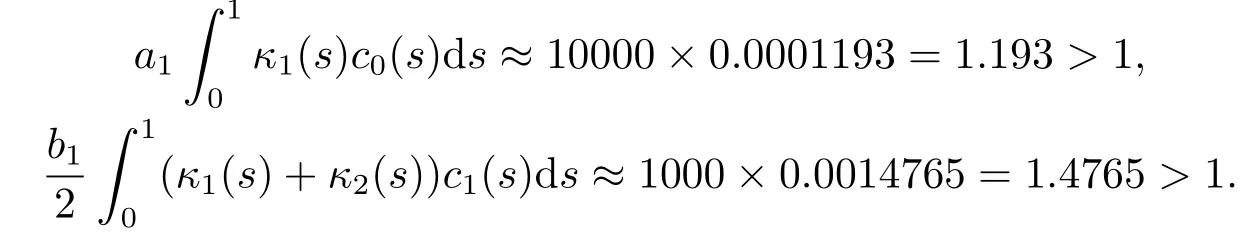
It follows that(3.3)is satisfied forC0large enough.Now takea2=2,b2=1, r=1.It is easy to check that (3.1) is satisfied.
Then BVP (4.1) has a positive solution by Theorem 3.1.

On the other hand, we have from Lemma 2.1 and 2.2 that foru ∈K{0}andt ∈[0,1],

and hence

Moreover foru ∈K{0}andt ∈[0,1],

and
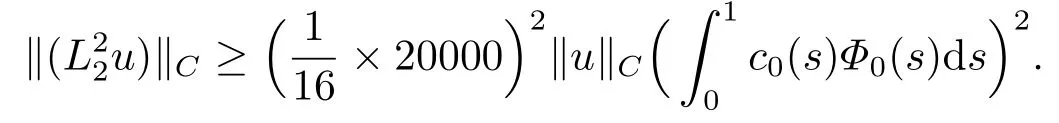
By induction,

Consequently, it follows that foru ∈K{0},

According to Gelfand’s formula, the spectral radius is

Then BVP (4.1) has a positive solution by Theorem 3.2.
- 应用数学的其它文章
- 不确定离散时间输入饱和系统的鲁棒预见控制
- Maximal Operator of (C,α)-Means of Walsh-Fourier Series on Hardy Spaces with Variable Exponents
- Empirical Likehood for Linear Models with Random Designs Under Strong Mixing Samples
- 带分数阶边值条件的差分方程组的正解问题
- An Interior Bundle Method for Solving Equilibrium Problems
- 纵向数据下非参数带测量误差的部分线性变系数模型的估计

