Schrdinger方程的连续时空有限元方法

关宏波, 郭昱杉, 曲双红

(郑州轻工业大学数学与信息科学学院, 河南 郑州 450002)

1.引言

其中Ω ⊂R2为有界凸区域,∂Ω为Ω的边界,T是总时间, i是虚数单位,u0=u0(x)是t= 0时刻的初值,u为未知函数,f为已知的右端源项, 这里及以后出现的函数均为复值函数.

对于时间相关的发展型偏微分方程, 连续时空有限元方法有着独特优势, 其主要思想是对时间变量和空间变量同时进行有限元离散, 而传统的全离散有限元格式则是对空间变量采用有限元离散, 对时间变量采用差分离散, 如果需要改变时间方向的计算精度, 其所对应的理论分析和数值计算差别较大, 重复性工作几乎成倍增长.而连续时空有限元方法的理论分析和数值计算对于任意阶的时间离散和空间离散都是统一处理和一致成立的, 该方法已被成功应用于热传导方程、波动方程、Sobolev方程、反应扩散方程等时间相关偏微分方程.[6]然而对于Schrdinger偏微分方程的时空有限元方法, 目前尚未见到有正式出版的文献进行报道.

2.连续时空有限元方法

首先, 本文所用到的Sobolev空间及范数的记号都是标准的.[7]另外, 我们着重介绍时空Sobolev空间及范数如下:

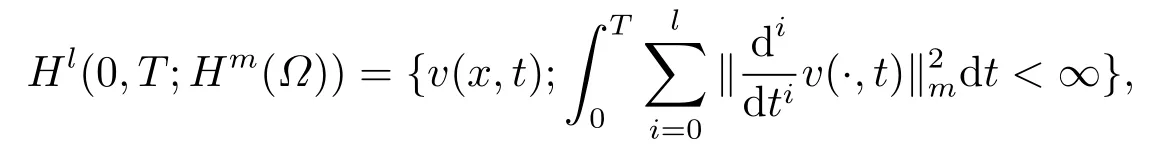
和

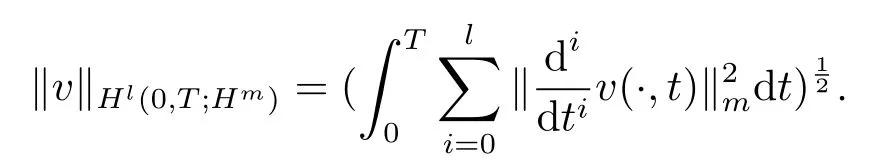
原问题(1.1)所对应的变分形式为: 求u ∈U, 使得

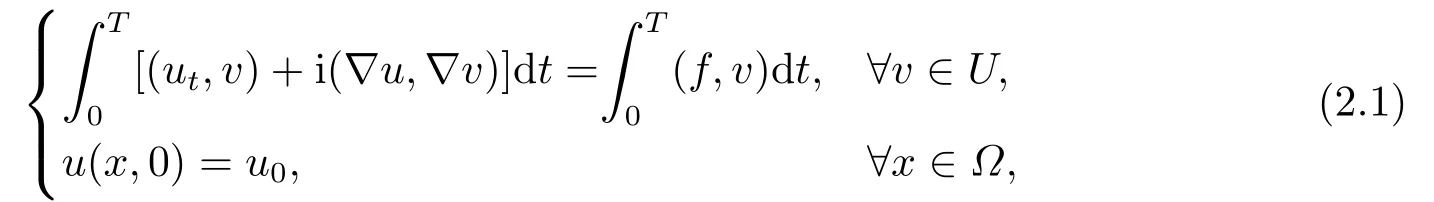
此外, 定义关于时间变量的投影算子Pt:H1(0,T)→Skl([0,T]), 易知Ptu(tn) =u(tn)(n=0,1,··· ,N).如果u ∈H1(0,T), 则成立:

同时, 对任意的u ∈Hs(0,T), 有

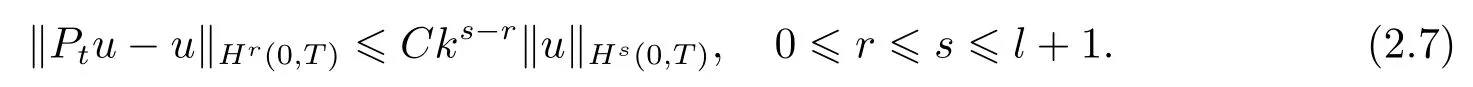
文[7]还证明了投影算子Px和Pt具有如下引理1中的逼近性质:

3.误差估计

下面进行连续时空有限元误差分析, 得到本文主要结论如下:

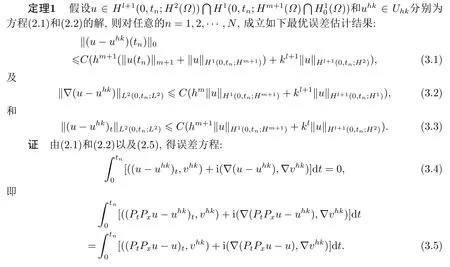
根据Pt和Px的定义, 上式可变形为

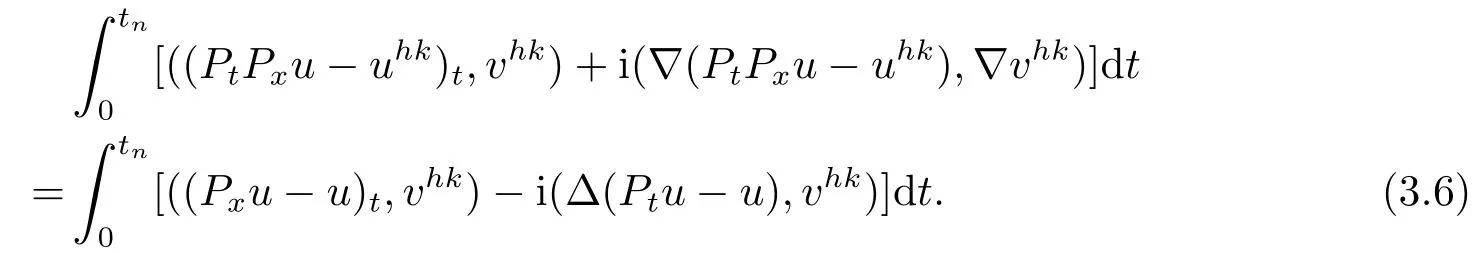
在(3.6)中取vhk=PtPxu-uhk, 可得

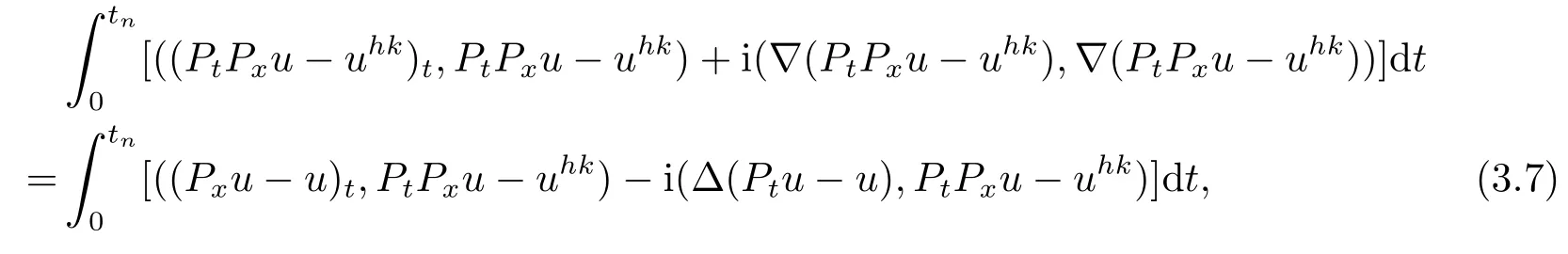
或

比较等式(3.7)两边的实部, 有

利用Gronwall不等式, 得

利用三角不等式及引理1, 有

定理1中第一个结论(3.1)得证.

即

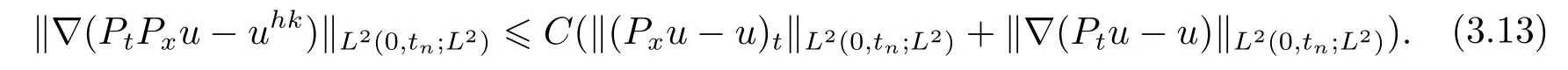
结合(3.13)与引理1, 得

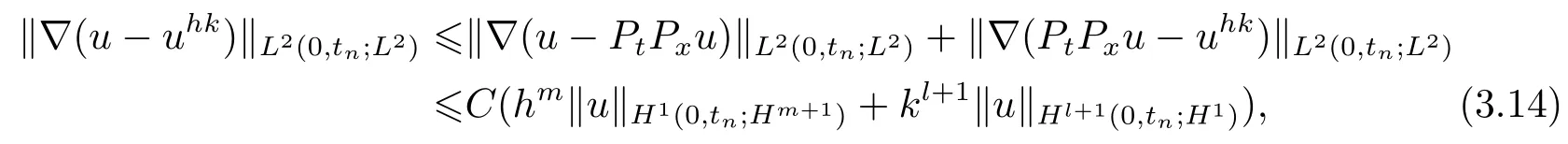
故结论(3.2)得证.

下面证明(3.3).

在(3.6)中取vhk=(PtPxu-uhk)t, 可得

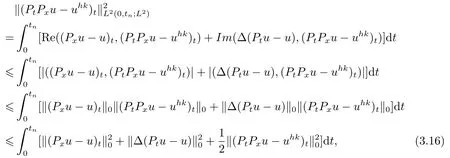
即

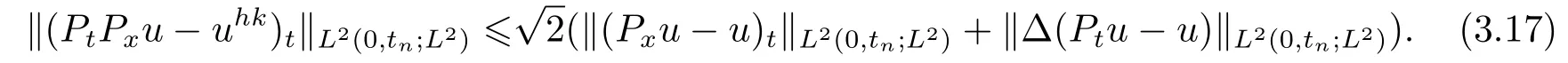
由(3.17)及引理1, 得

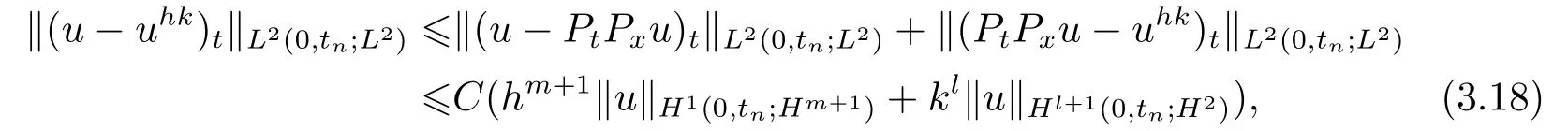
结论(3.3)得证.至此定理证毕.

4.小结

1) 如果对空间区域采用低阶非协调元逼近, 如矩形元[8]、CNQr1ot矩形元[9]或非协调P1三角形元[10], 则其对应的有限元插值算子等价于文中针对空间变量的椭圆投影算子Px,从而会使得理论分析变得更为简洁.另外, 由于上述两个矩形单元满足相容误差比插值误差高一阶的特殊性质[11], 且具有各向异性特征[12], 我们还可以得到其在各向异性网格下的整体超逼近和超收敛性质.