Boundedness of Commutators of Variable Anisotropic Caldern-Zygmund Operators

YANG Zhenzhen(杨珍珍), SUN Jawei(孙嘉伟), LI Baode(李宝德)

(College of Mathematics and System Science, Xinjiang University, Urumqi 830017, China)

Abstract: Let T be a variable anisotropic Caldern-Zygmund operator associated with a continuous multi-level ellipsoid cover Θ of Rn.Ellipsoids in Θ can change shape rapidly from level to level and from point to point.Suppose [b, T] is a commutator of T and some Lip-function b.In order to obtain the boundedness of [b, T] on some function spaces, by using real variable methods of harmonic analysis, the boundedness of commutators [b, T]from variable anisotropic Hardy spaces to Lebesgue spaces and from variable anisotropic Hardy spaces to weak Lebesgue spaces in critical cases are obtained.These results are variable anisotropic extension of corresponding results under isotropic setting.

Key words: Anisotropy; Hardy space; Continuous ellipsoid cover; Singular integral operator; Commutator

1.Introduction

On the Euclidean space Rn, the standard Caldern-Zygmund operatorTis defined by

whereΩ ∈C2(Sn-1) is homogeneous of degree zero and has mean value zero on the unit sphere.The commutator generated by a locally integrable functionband the operatorTis defined by

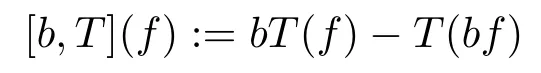
for suitable functionsf.As we all know,it plays an important role in harmonic analysis[14-15]and has important applications in the estimates of the solutions for the elliptic equations and some nonlinear PDEs[4-5,10].

In 1976, a classical result was that Coifman et al.[6]presented the commutator [b,T] is bounded fromLp(Rn) to itself withp ∈(1,∞), whereb ∈BMO(Rn) andTis the classical Caldern-Zygmund operator.Then, Harboure et al.[11]proved that [b,T] is bounded from Hardy spacesH1(Rn) to Lebesgue spacesL1(Rn) if and only ifbequals to a constant almost everywhere.This means that [b,T] is not bounded from Hardy spaces to Lebesgue spaces.

Inspired by [14], we are interested extending this result to a more general situation on Rnand find the more general Hardy spaces, the singular integral operator and the Lipschitz function.Fortunately, the most general class of (unweighted) Hardy spaces on Rndefined for the entire range of 0＜p ≤1 are spaces with pointwise variable anisotropy developed by Dekel, Petrushev, and Weissblat[8].More precisely, they correspond to the largest class of spaces of homogeneous type on Rnequipped with Lebesgue measure for which Hardy spaces were developed for all 0＜p ≤1.These spaces are constructed over multi-level ellipsoid covers of Rnthat are highly anisotropic in the sense that the ellipsoids can change shape rapidly from point to point and from level to level, which unites the classical anisotropic Hardy spaces studied by Fefferman,Stein and generalizes previous work on anisotropic Hardy spaces of Bownik[1], so it makes sense to study Hardy spaces and their properties related to multi-scale ellipsoids.And recently, Bownik et al.[3]further introduced a class of singular integral operators adapted to this ellipsoid covers of Rn, a more general singular integral operator, is defined by

whose kernelK(x,y) satisfies the bound

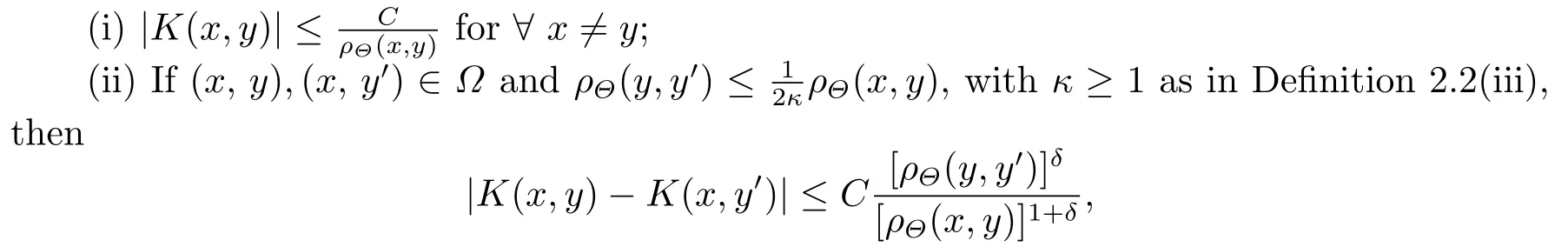
whereδandCare positive constants, andρΘis as in (2.3).

Then,we introduced a class of Lipschitz function Lipβ(Θ)adapted to this ellipsoid covers of Rn, a more general Lipschitz function, is defined by

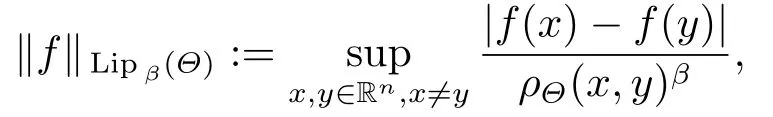
whereρΘis as in (2.3).So, we can also extend to the homogeneous space, but for simplicity we extend the bounded results of commutators to the most generalHp(Θ) space.

It is worth pointing out that in order to obtain the relative boundedness of commutators,the usual method is to borrow the proof methods in [2, 13].We need to prove that the finite atom decomposition and the infinite atom decomposition in the Hardy space of the finite atom are equivalent.It can be further extended from the uniformly boundedness of the commutator on the atom to the boundedness of Hardy space.Inspired by [3], we find a better decomposition in Hardy space, by using an improved atomic decomposition of anyf ∈Hp(Θ)∩Lq(Rn),which converges in the sense of distribution andLq(Rn)norm.With the help of this result and its uniform boundedness on the atom, we can extend the boundedness results for commutator [b, T].

To be precise, this article is organized as follows.

2.Preliminaries

In this section we recall some notion, notations and basic properties on continuous ellipsoid coversΘ(see, for example, [7-8]), quasi-distanceρΘthat are used throughout the paper and the definition ofHp(Θ).Then, we introduce the variable anisotropic singular integral operators and Lipschitz functions, which are associated with a continuous ellipsoid coverΘ.An ellipsoidθin Rnis an image of the Euclidean unit ball Bn:={x ∈Rn:|x|＜1}under an affine transform, i.e.,

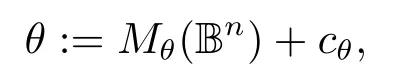
whereMθis a nonsingular matrix andcθis the center.

Let us begin with the definition of continuous ellipsoid covers,which is from[7,Definition 2.4].

Definition 2.1We say that

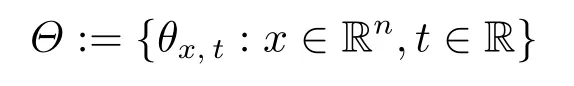
is a continuous ellipsoid cover of Rn, or shortly a cover, if there exist constants p(Θ) :={a1,...,a6}such that:

(i) For everyx ∈Rnandt ∈R, there exists an ellipsoidθx,t:=Mx,t(Bn)+x, whereMx,tis a nonsingular matrix andxis the center, satisfying

(ii) Intersecting ellipsoids fromΘsatisfy a “shape condition”, i.e., for anyx, y ∈Rn,t ∈R ands ≥0, ifθx,t ∩θy,t+sthen

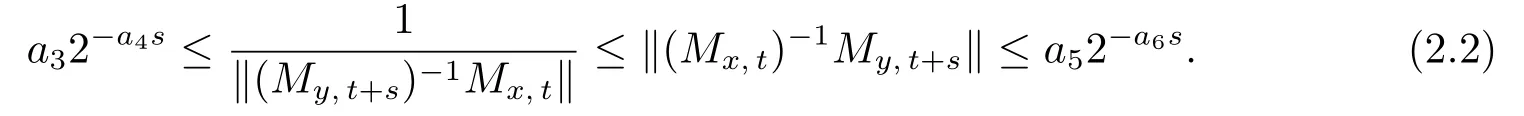
Here,‖·‖is the matrix norm ofMgiven by‖M‖:=max|x|=1|Mx|.

Next we collect results about ellipsoid covers from [7-8] which will be used subsequently.

Lemma 2.1LetΘbe a continuous ellipsoid cover.

(i) Then there existsJ:=J(p(Θ))≥1 such that, for anyx ∈Rnandt ∈R,

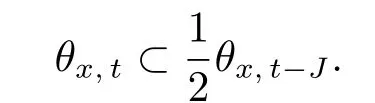
(ii) For anyx,y ∈Rnands,t ∈R witht ≤s, ifθx,t ∩θy,s∅, there exists a constantγ ＞0 such that

θy,s ⊂θx,t-γ.

Definition 2.2A quasi-distance on a setXis a mappingρ:X ×X →[0,∞) that satisfies the following conditions for allx,y,z ∈X:

(i)ρ(x,y)=0⇔x=y;

(ii)ρ(x,y)=ρ(y,x);

(iii) For someκ ≥1,ρ(x,y)≤κ(ρ(x,z)+ρ(y,z)).

Lemma 2.2[3,7-8]LetΘbe a continuous ellipsoid cover.

(i) The functionρ: Rn×Rn →[0,∞) defined by

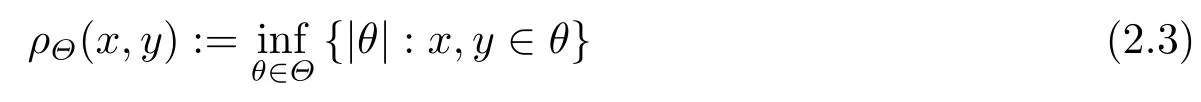
is a quasi-distance on Rn.

(ii) LetΘbe a continuous ellipsoid cover and letρΘbe a quasi-distance as in (2.3).For anyx ∈Rn,r ＞0 and ball

there existt1,t2∈R such that

where equivalence constants depend only on p(Θ).

(iii) Letz ∈Rn,t ∈R andy ∈θz,t.Then, for anyk ∈N we have

whereγis as in Lemma 2.1(ii).

In particular, ifx ∈θz,t-(k+1)γ θz,t-kγfor somek ∈N, then

Now, we recall the definition of Hardy spaces with variable anisotropy which were originally introduced by Dekel, Petrushev and Weissblat[8].

Definition 2.3LetN,∈N0withN ≤and

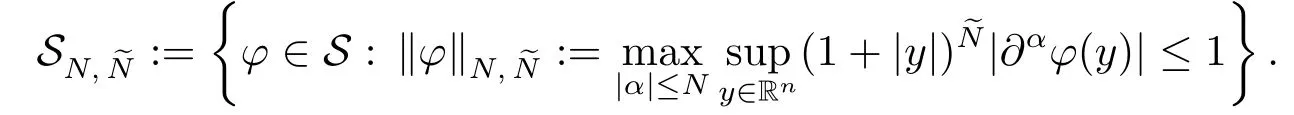
For eachx ∈Rn,t ∈R andθx,t=Mx,t(Bn)+x ∈Θ, denote

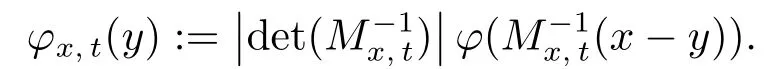
Definition 2.4Letf ∈S′andφ ∈S.The radial maximal function offis defined by

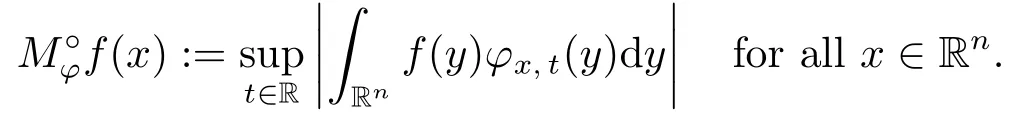
Lemma 2.3[8]The dual space ofH1(Θ) is BMO(Θ).

Definition 2.6Let 0＜p ＜∞.The weakLpspace is defined by{f:‖f‖W Lp ＜∞},where

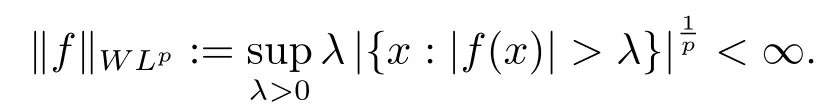
Now,we show that the definition of singular integral operators in the setting of continuous ellipsoid covers is consistent with the Caldern-Zygmund operators on spaces of homogenous type, see Lemma 2.2.

Definition 2.7[1]We call that a locally square integrable functionKonΩ:={(x,y)∈Rn ×Rn:is called a variable anisotropic singular integral kernel with respect to a continuous ellipsoid coverΘif there exist positive constantsδandCsuch that

(i)|K(x,y)|≤for;

We say thatTis a variable anisotropic singular integral operator ifT:L2→L2is a bounded linear operator if there exists a kernelKsatisfying Definition 2.7 such that

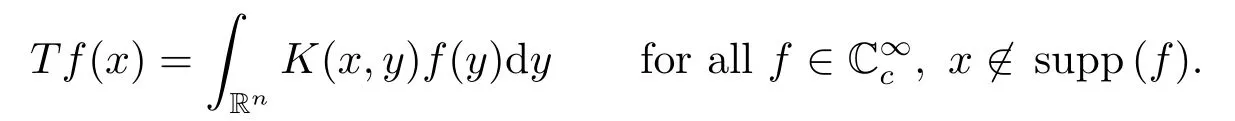
The fundamental theorem about singular integral operators, which holds on arbitrary spaces of homogeneous type, asserts thatTis also bounded fromL1to weak-L1.Then, the Marcinkiewicz interpolation theorem implies thatTis bounded fromLqtoLqfor 1＜q ≤2.Thus, by Theorem 5.2 in [3], we have the following theorem.

Theorem 2.1LetTbe a variable anisotropic singular integral operator and 1＜q ≤2.ThenTextends to a bounded linear operator fromL1toWL1and fromLqtoLq.

Definition 2.8Letβ ＞0.Lipschitz space Lipβ:= Lipβ(Θ) is defined by{f:‖f‖Lipβ ＜∞}, where

We are now ready to state the main results of the paper-Theorems 2.2, 2.3 and 2.4.These are generalizations of Lemma 12 in [12], Theorems 2.1 and 2.3 in [14] to Hardy spaces with pointwise variable anisotropy of Dekel.

3.Proofs of Theorems

To prove Theorem 2.2, we need Lemma 3.1 as follows.

Lemma 3.1Let 0＜β ＜1 and

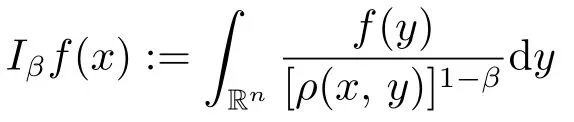
ProofThe proof of Lemma 3.1 is almost identity with that of Lemma 2.1 in[9].This is mainly due to the fact that the ballBρΘ(x, r)here and the ballB(x,r)={y ∈Rn:ρ(y-x)＜r}in [9] both satisfy

By this and following the proof of Lemma 2.1 in [9], we may finish the proof of Lemma 3.1.

Proof of Theorem 2.2We show this proposition by borrowing some ideas from the proof of Lemma 12 in [12].Letf ∈Lp.Then, for anyx ∈Rn, we have

which implies that

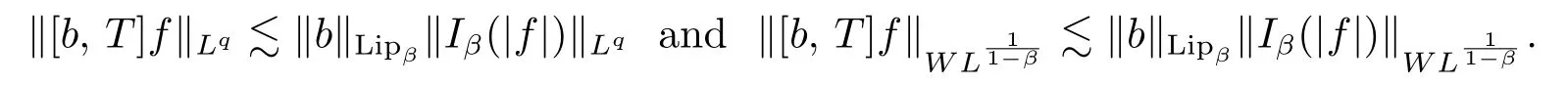
Applying the boundedness ofIβfromLptoLqand fromL1to weak(see Lemma 3.1),we futher obtain

and hence complete the proof of Theorem 2.2.

To prove Theorem 2.3, let us begin with some lemmas.

Lemma 3.2[3]LetΘbe a continuous ellipsoid cover and 0＜p ≤1.

(i) The inclusionHp(Θ)is continuous;

(ii)Hp(Θ) is complete.

Lemma 3.3[3]Let 0＜p ≤1 and 1≤q ＜∞.The subspaceHp(Θ)∩Lqis dense inHp(Θ).

As in the classical case, the anisotropic Hardy spaces can be characterized and then investigated through atomic decompositions.The following Definitions 3.1 and 3.2 come from Definitions 4.1 and 4.2 in [8], respectively.

Definition 3.1For a continuous ellipsoid coverΘ, we say that (p,q,l) is admissible if 0＜p ≤1≤q ≤∞,p ＜qandl ∈N0, such thatl ≥NpwithNpas in (2.7).A (p,q,l)-atom is a functiona: Rn →R such that

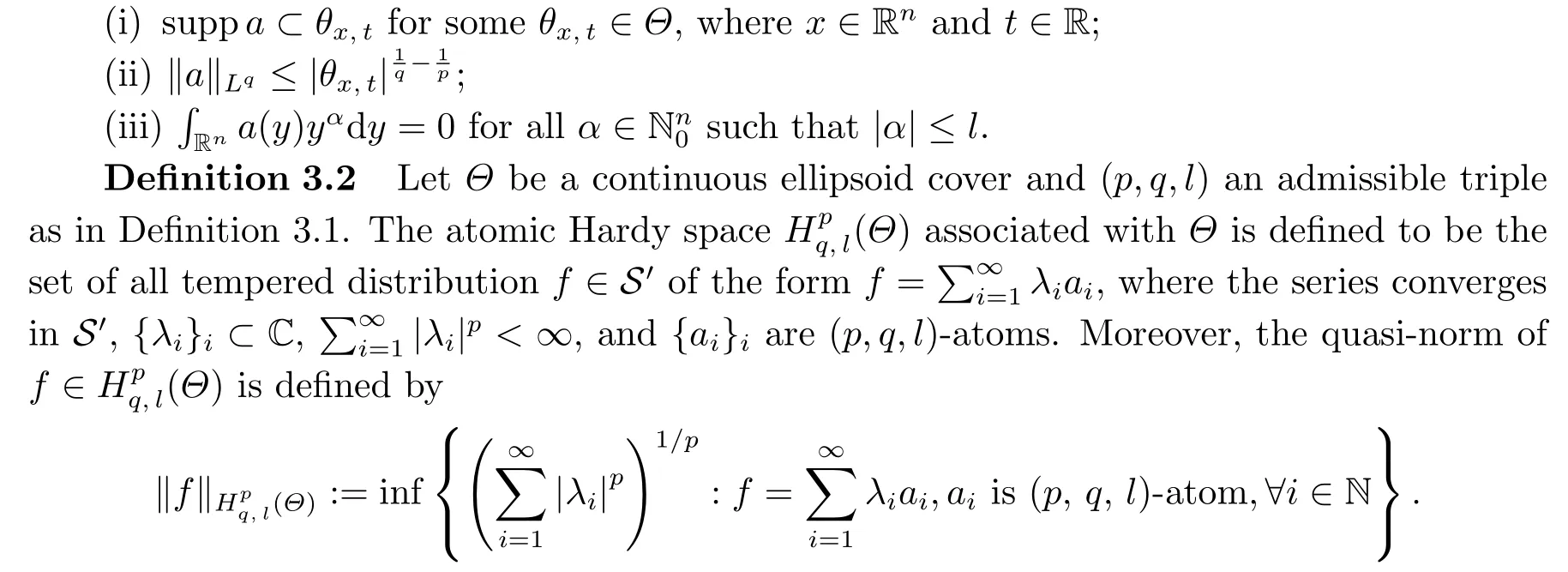
The following theorem due to Theorems 4.4 and 4.19 in [8] shows the atomic characterization ofHp(Θ).

ProofWe show this lemma by borrowing some ideas from the proof of Theorem 2.1 in[14].Letl ≥Npand letabe a (p,2, l)-atom with suppa ⊂θz,t, wherez ∈Rnandt ∈R.Then, we have

whereγis as in Lemma 2.1(ii) andk0∈N will be fixed later.

Next, we turn to show the estimate of I2.

For anyx ∈(θz,t-k0γ)C, by Lemma 2.1(ii), there exists somek ∈N0such thatx ∈θz,t-(k+k0+1)γ θz,t-(k+k0)γ.First, for anyy ∈θz,t, we first prove

uniformly for somek0∈N depending only onκand p(Θ).Indeed, by (2.1) and (2.6), we have

Thus, to guarantee that(3.4) holds, it suffices to let

hold, which implies that

and hence whenk0is sufficiently large, (3.4) holds.

By (3.4), Definitions 2.8 and 2.7, (2.6), (3.5), Hlder’s inequality and Definition 3.1, we obtain

Therefore, by (2.6), (3.5) and (3.6), we have

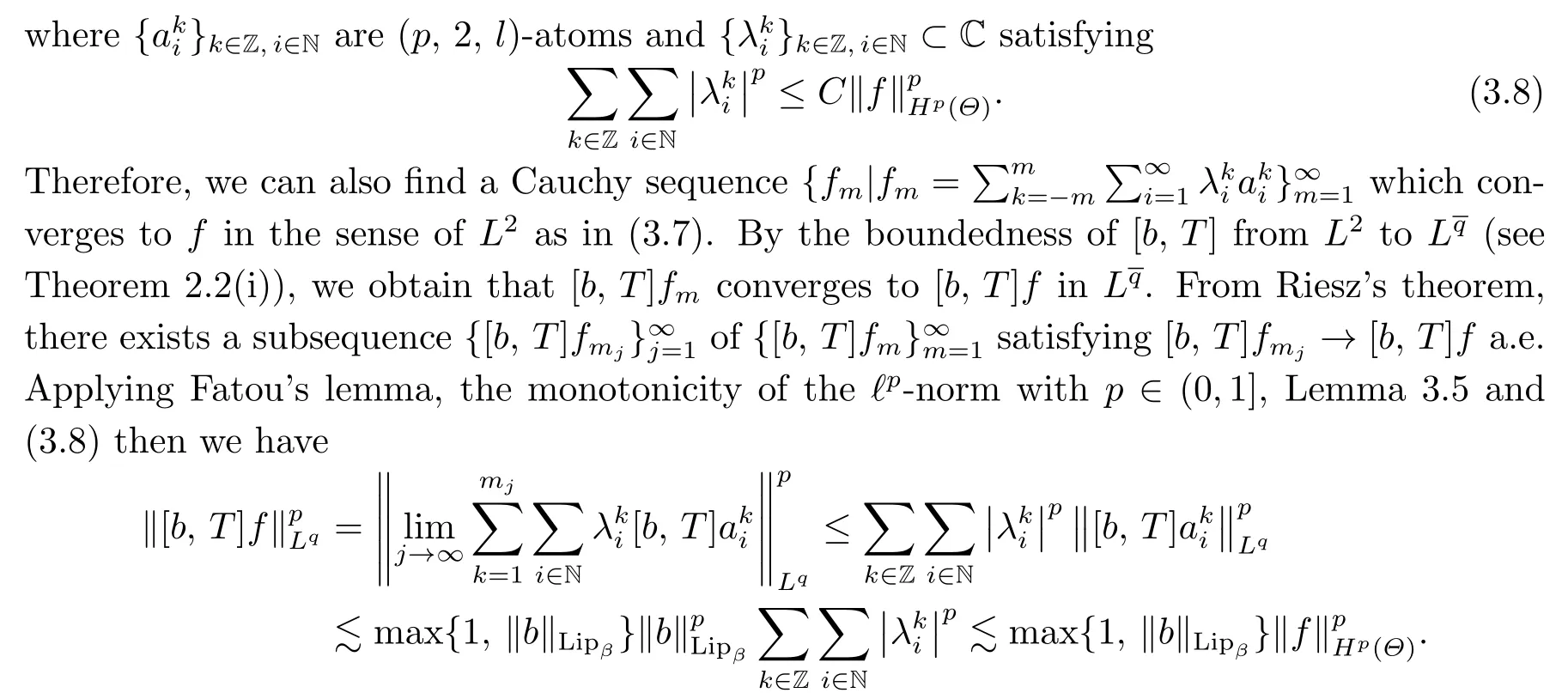
By this, the density ofHp(Θ)∩L2inHp(Θ) (see Lemma 3.3) and the completeness ofHp(Θ)(see Lemma 3.2(ii))andLq,we deduce that[b, T]extends to a bounded linear operator fromHp(Θ) toLq, which completes the proof of Theorem 2.3.

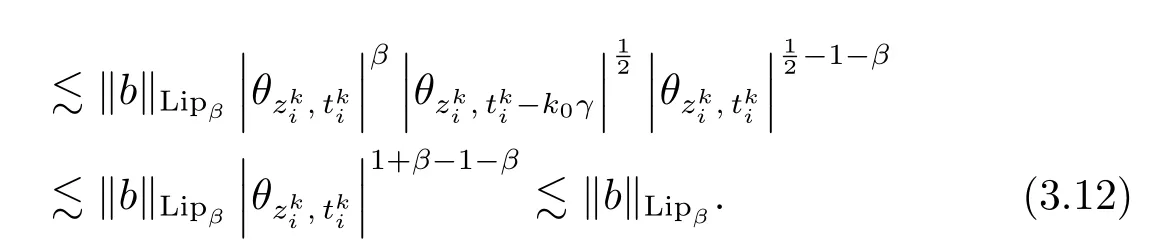
For the term J2(x), partial using the estimate of I2of the proof of Theorem 2.3 withq=1, we conclude that

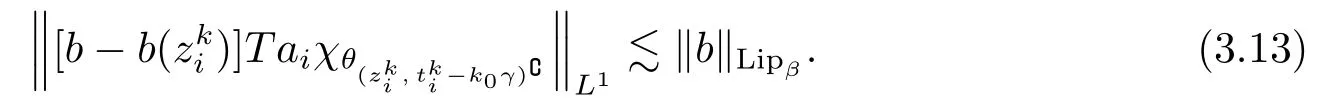
Thus, by (3.12), (3.13) and (3.9), we have

To deal with J3(x), by Definition 2.8, Hlder’s inequality, (2.3) and Definition 3.1(ii), we obtain

By (3.15) and the boundeness ofTfromL1toWL1, we have

For any(Θ)∩L2, now let us show

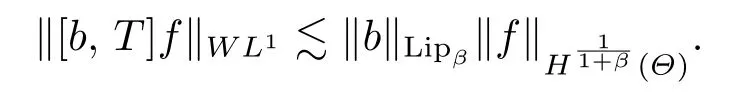
By (3.17) and (3.10), we have