点电流源直流场的三维正演模拟及可视化的初步研究
李靖炜,谢兴兵,高文龙
(长江大学 地球物理与石油资源学院,油气资源与勘探技术教育部重点实验室,湖北 武汉 430100)
0 引言
直流电阻率法是电法勘探中使用较广,较成熟的一种物探方法[1-2]。其通过人工建立的稳定电场探测岩矿石反应的电学性质差异,来获取地质结构信息[3-13]。随着仪器发展和勘探需求的进步,三维正反演是适应复杂地质条件下勘探的必要技术手段,且通过三维正演算法,对地质模型进行三维可视化处理,可以很好的帮助研究人员理解地质模型电阻率的空间分布。近半个世纪以来,国内外已有很多学者使用有限元法(FE,Finite Element)、有限差分法(FD,Finite Difference)、积分方程法(IE,Integral Equation)等数值模拟方法,包括一次场法和异常电位法[7,10],结构化网格和非结构化网格等对该问题进行了研究,并取得丰富的成果[3-19]。
本文基于有限差分法实现了直流电阻率的三维正演模拟及可视化,有限差分数值模拟方法具有较快的计算速度、编程实现简单、占用的物理存储空间相对较小等特点,同时也是应用较广泛、研究较多的一类数值模拟方法。对于使用有限差分法进行直流电法三维正演问题,Dey等[3]对于该模拟问题进行了有限差分法三维数值模拟,但其求解差分格式的线性方程时效率很低。周熙攘等[5]对于该模拟问题详细论述了有限差分法数值模拟方法及该方法的优缺点,并使用Fortran语言做了正演计算。Zhao等[10]和吴小平等[12,20]对该三维模拟问题优化了有限差分大型稀疏方程组的求解算法。邓正栋等[21]对该问题进行了点源三维有限差分及异常电位法[7,10,22]的详细推导,并做了一维验证。王志刚,何展翔,魏文博等[23]对于该模拟问题进行了算法及求解方法等若干讨论。朱占升等[17]通过MATLAB平台对电法勘探数据进行了三维可视化处理,但其使用的面绘制很难对空间内部等进行多视角观察。鉴于此,本文从异常电位所满足的微分方程出发,采用有限差分算法进行直流电阻率的三维数值计算,在MATLAB下编程使得数值计算及三维可视化同时进行。在此基础上,期望借助于MATLAB GUI编程实现具有三维视电阻率多角度显示功能的直流电法三维数值模拟系统,帮助研究人员能够更加方便、直观和快捷地理解不同地球物理模型的电阻率的空间分布及其变化规律。
1 控制方程
对于均匀半无限空间中点源分布电流场的计算问题,一般需要把计算区域限定在有限的空间,即在一个有限的求解区内求解对应的方程,结合物理和数学的要求,对相应的边界上规定边值,确定方程的唯一解。
求解的空间模型见图1。图1中的Ⅰ和Ⅱ区域分别代表不同电导率分布的异常体空间和背景空间,使用异常电位法,将电位分为背景电位U0和异常电位Ua,即U=U0+Ua,σa表示实际电导率σ减去背景电导率σ0,即σa=σ-σ0,T0,T1…T5依次分别代表空间模型的上边界、左边界、前边界、右边界、下边界和后边界。
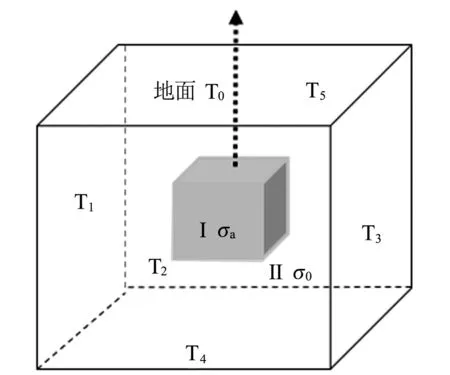
图1 三维直流电法求解空间模型
在三维笛卡尔坐标系中,若地下均匀半空间中场源是一个坐标位于地面(x0,y0,z0)点,电流强度为I的点电流源,通过推导可得到异常电位Ua满足的微分方程(1):
∇·(σ∇Ua)=-∇·(σa∇U0)
(1)
边界条件满足方程(2):
(2)
其中:σ=σ(x,y,z),U=U(x,y,z)。在正演计算中U0,σa和σ和边界条件是给定的,只有Ua是未知数,所以异常电位Ua的解是唯一的。
2 有限差分法数值模拟
点电流源的电位在三维空间满足的方程及定解条件在数学上称为求解偏微分方程的边值问题。本文采用有限差分法解决此边值问题。有限差分法是用差商代替微分,把理论上的电场微分方程变换为适于数值计算的差分形式,形成能够数值计算的差分方程。
在电法勘探三维正演模拟中根据有限差分中剖分网格形式的不同,可以分为交错网格[24]、常规网格、无网格差分[25]等。综合分析算法的计算成本及对硬件的要求,本文选择使用常规六面体网格进行有限差分。
2.1 剖分网格
为便于计算,需要对求解区域进行网格剖分,将电位U赋值于六面体网格节点上。数值计算中使用符号i、j和k对每个节点编号,区分表现为网格节点沿X、Y和Z轴方向的编号,令hi=Δxi、hj=Δyj和hk=Δzk示网格节点U(xi,yj,zk)沿X、Y和Z轴正方向的步长,网格节点电位Ui,j,z=U(xi,yj,zk);单元电导率σi,j,z=σ(xi,yj,zk)。网格剖分样式见图2,对于小体积异常体,对异常体部分进行细小的网格剖分,对异常体之外的部分使用常规剖分。

图2 网格示意图
2.2 差分格式
通过对异常电位微分方程(1)的差分变换,得到线性方程(3):
[A]·{Ua}=-[Aa]·{U0}
(3)
在数值计算中,需要注意边界内的节点电位与边界上的节点电位的计算。当节点(i,j,k)位于边界内时,线性方程(3)中的矩阵 [A]、[Aa]和{Ua}为
[A]=[ai,j,kai-1,j,kai,j-1,kai,j,k-1ai+1,j,kai,j+1,kai,j,k+1]
(4)
式中:
hi表示沿i方向的步长,
ai,j,k=-[ai-1,j,k+ai,j-1,k+ai,j,k-1+ai+1,j,k+ai,j+1,k+ai,j,k+1],
其余(i,j,k)相邻节点系数与此类似。
{Ua}=[Uai,j,kUai-1,j,kUai,j-1,kUai,j,k-1Uai+1,j,kUai,j+1,kUai,j,k+1]T
(5)
[Aa]=[aai,j,kaai-1,j,kaai,j-1,kaai,j,k-1aai+1,j,kaai,j+1,kaai,j,k+1]
(6)
式中:
aai,j,k=-(aai-1,j,k+aai,j-1,k+aai,j,k-1+aai+1,j,k+aai,j+1,k+aai,j,k+1),
其余(i,j,k)点相邻系数形式与其相似。
当节点(i,j,k)位于地面T0边界上时,因为地面节点是半个单元,空间中不存在(i,j,k-1)节点,同时场源位于地面,其满足镜像法原理[5],所以在地面边界上,其相应的节点点电流源的电流强度放大一倍,线性方程(3)中的矩阵 [A]、[Aa] 和 {Ua} 为
[A]=[ai,j,kai-1,j,kai,j-1,kai+1,j,kai,j+1,kai,j,k+1]
(7)
式中:
ai,j,k=-(ai-1,j,k+ai,j-1,k+ai+1,j,k+ai,j+1,k+ai,j,k+1),
其余(i,j,k)相邻系数形式与其相似。
同理,{Ua} 中没有Uai,j,k-1节点,其中aai,j,k+1为
{Ua}=[Uai,j,kUai-1,j,kUai,j-1,kUai+1,j,kUai,j+1,kUai,j,k+1]T
(8)
[Aa]=[aai,j,kaai-1,j,kaai,j-1,kaai+1,j,kaai,j+1,kaai,j,k+1]
(9)
式中:
aai,j,k=-(aai-1,j,k+aai,j-1,k+aai+1,j,k+aai,j+1,k+aai,j,k+1),
其余(i,j,k)相邻系数形式与其相似。
当节点(i,j,k)位于T1,T2,…,T5边界上时,此类边界面上不存在场源,进行数值计算时所设异常模型距离边界面相对较远,所以令异常电位Uai,j,k=0,令边界面上的电位等于U0。
在电导率不同的分界面上,因为差分过程中是对节点及其相邻节点进行差商代替,所以在差分方程中电位在此分界上是自然连续的。
结合参数矩阵(4)~(9)求解线性方程(3)即可确定异常场电位,最后将有限差分法求得的异常场电位Ua与解析解求得的正常场电位U0相加,可以近似得到实际电场电位U。
2.3 线性方程组的求解
本文选取逐次超松弛(Successive Over Relaxati-on, SOR)迭代法[4]求解线性方程(3)。点电流源三维数值模拟离散网格的节点总数一般可达百万级别,形成的矩阵为巨型稀疏阵,线性方程组的阶数很高,若直接求取,虽然速度较快,但占用内存量较大,累计误差也较严重。若选用常规迭代法求解,占用内存少,编制程序较简单,也可以克服误差的累积,但收敛速度较慢。在保持迭代的优点基础上,为加快收敛速度,选取SOR迭代法。超松弛迭代法首先对每一个节点上的电位赋予初值(本文异常电位Ua初值赋予0),而后依照节点编号依次由差分方程求解各节点的电位,从而每一个节点通过超松弛迭代计算该节点的电位值:
(10)

3 算例
为了验证算法的正确性,通过使用二级装置,得到三维视电阻率数据,然后,三维数值模拟结果与解析解一维视电阻率曲线对比并检验算法是否正确。
模型Ⅰ:空间范围100 m×100 m×100 m,点源位于地面T0中心(空间模型见图1),背景电阻率300 Ω·m,低阻球形异常体电阻率30 Ω·m,半径10 m,球心埋深50 m(点源正下方)。
通过数值计算求得三维视电阻率数据,过点源取一垂直切片,由图3可见,红线框标识了异常体大致位置(点源位于异常体正上方),从图中可以明显看出低阻异常体位置以及视电阻率的连续性变化,这可以说明算法是适合的;通过数值解与解析解对比验证,得到一维视电阻率对比曲线,由图4可见,从视电阻率ρs曲线上来看,数值解具有较好的对称性(图4a),从相对误差来看,其相对误差在0.5%以内(图4b),说明三维数值计算的精度相对较高,用于研究异常体的变化规律和可视化是可行的。

图3 差分数值解三维视电阻率切片
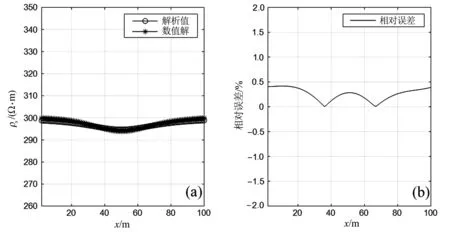
图4 差分数值解与解析解对比
模型Ⅱ:空间范围100 m×100 m×100 m,点源位于地面T0中心,背景电阻率300 Ω·m,使用两个立方体异常模型,低阻30 Ω·m,高阻300 Ω·m,异常体边长均为10 m,体中心埋深均为50 m。
为进一步验证算法,使用模型Ⅱ的组合异常体模型。异常体位于点源正下方的两侧,通过二级装置计算得到三维视电阻率,平行X轴取过点源与两个异常体的切片见图5,红线框标识了异常体大致位置。从图5中可以明显分辨出低阻体和高阻体,及其空间位置和异常体视电阻率的形态,这也说明当空间存在组合异常体时,该算法依然是可行的。

图5 组合异常体三维视电阻率切片
4 可视化及MATLAB GUI界面
可视化即对数值计算的三维数据体进行三维可视化,图6是算例1中低阻球形异常体视电阻率3D等值线可视化图,其主要使用MATLAB的函数“contourslice”对视电阻率三维数据进行可视化处理。结合MATLAB GUI开发应用,即使用GUI图形对象组成用户界面,通过这种用户界面,三维数值模拟的命令和对程序的控制是通过“选择”各种图形对象来实现的。

图6 低阻异常体视电阻率三维等值线可视化
4.1 GUI开发环境
本文使用MATLAB平台,其GUIDE(GUI Development Environment)提供了一套可视化的创建图形窗口(GUI)的工具,包括布局编辑器(Layout Edtor)、几何排列工具(Alignment Tool)、属性编辑器(Property Inspector)、对象浏览器(Object Browser)及菜单编辑器(Menu Editor),使用GUIDE可方便创建GUI应用程序。在MATLAB中,GUI的设计是以M文件的编程模式完成的,它能够按照用户设计的GUI布局,将GUI的布局代码存储在FIG文件中,同时产生一个M文件用于存储调用函数,在M文件中不再蕴含GUI的布局代码。利用这一框架编制自己的应用程序,在开发应用程序时代码量大大缩小。
4.2 开发流程
GUI图形界面的功能,还是要经过一定的设计思路和计算方法,由特定的程序来完成。开发GUI应用流程图见图7(Z轴表示深度,二极装置等效于AO的距离,为更贴合地下三维空间,笔者使用三维笛卡尔坐标表示),为了实现程序的功能,需要通过GUIDE完成操作界面的布局及控件的标识,还需要在运行程序前编写有限差分三维模拟算法代码,完成程序中变量的赋值、输入输出、计算及绘图等工作,最终实现数据可视化。
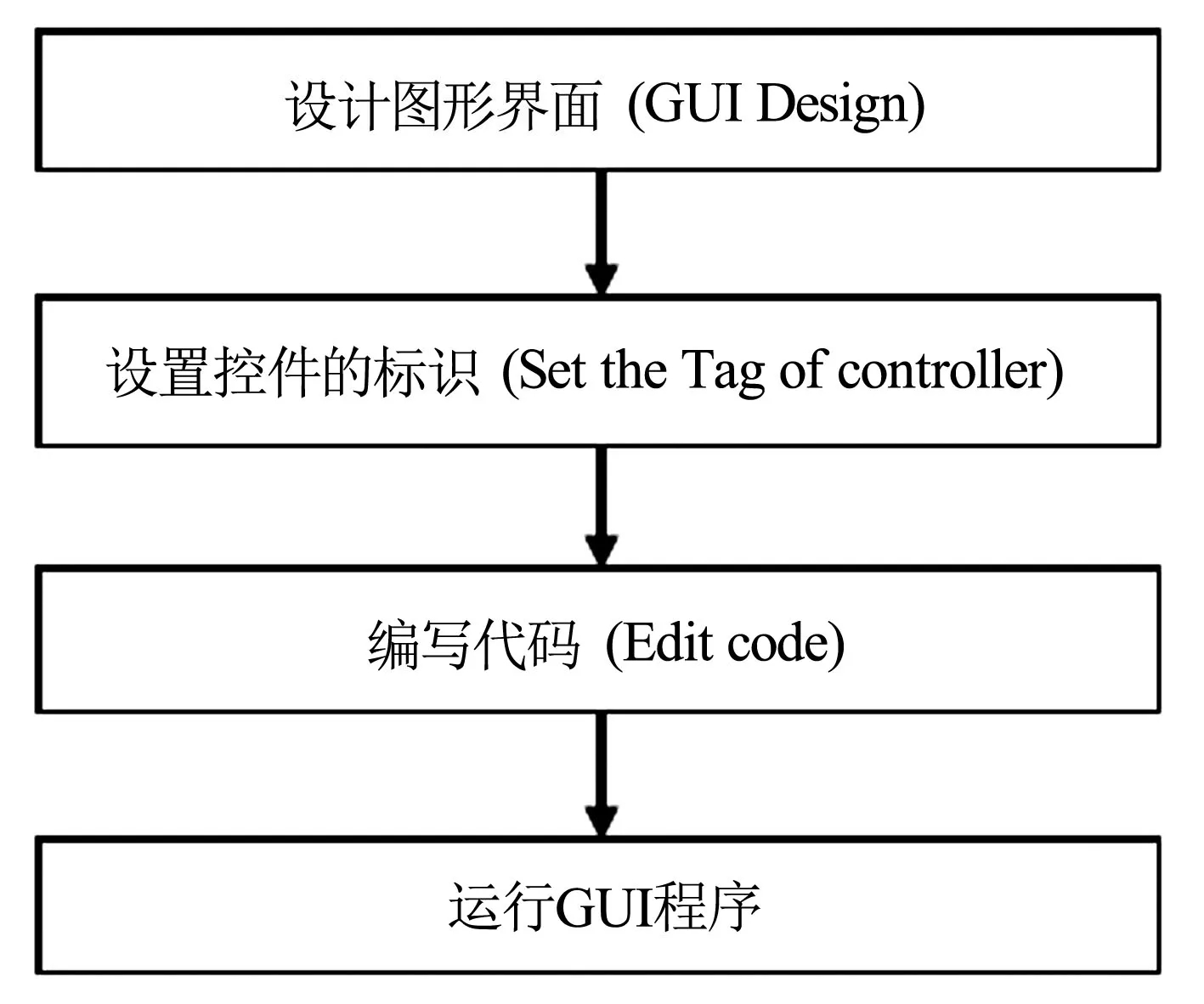
图7 GUI应用开发流程图
4.3 应用
运行程序(平台MATLAB),通过命令窗口直接输入文件名或用openfig,open或hgload命令即可运转GUI程序。
在模拟实验中,通过点击不同的菜单栏选项,可以得到对应的视电阻率三维可视化图。不同的菜单对应不同的模拟实验,部分三维直流视电阻率可视化程序操作界面见图8。同时,使用者可在对应的文本框中设置电阻率参数等,这样使得操作者不必对算法有深入的认识,可以通过参数设置等对其快速的模拟,这也是GUI界面的优点。相反,该应用程序也有一些小缺点是可移植性差,对于MATLAB开发的GUI界面程序,其依赖于MATLAB Mathworks工作平台,即使包装成“.exe”Windows程序,其仍需要安装MATLAB相关辅助程序。

图8 三维直流视电阻率可视化程序界面
5 结论
本文使用经典的有限差分法、异常电位法和SOR迭代求解三维数值模拟问题,论述了数值计算过程及GUI开发过程,目的不是追求在算法上进行创新和突破,而是在于通过具有丰富的可视化包的MATLAB平台进行视电阻率三维数值模拟及可视化,来避免使用第三方软件建模或成图带来的不便。同时,由三维正演模型,可以得到很多有意义的三维直流电法响应的相关结论。
1)通过算例分析表明,基于MATLAB使用有限差分对视电阻率进行三维数值模拟及可视化,不仅是可行的,而且算法简单有效,同时三维数值计算的结果也具有很高的精度。
2)通过对离散异常电位微分方程得到的系数矩阵研究,使用SOR迭代法,其差分格式通过MATLAB编程不仅不用考虑对大型稀疏系数矩阵进行压缩储存,而且计算速度较快。
此外,笔者编写的三维可视化GUI应用程序只是一个初级阶段,但已具备方便快速的计算、多角度直观的三维可视化、简约的操作界面等诸多优点,有信心通过加入更多的三维数值计算模块以及对MATLAB可视化编程和GUI编程的深层次开拓,其能够形成功能更为全面的三维数值模拟可视化系统。

